Hostname: page-component-848d4c4894-m9kch Total loading time: 0 Render date: 2024-05-09T03:24:35.627Z Has data issue: false hasContentIssue false
  • English
  • Français

A bathtub vortex under the influence of a protruding cylinder in a rotating tank

Published online by Cambridge University Press:  18 September 2013

Yin-Chung Chen ,
Shih-Lin Huang ,
Zi-Ya Li ,
Chien-Cheng Chang  and
Chin-Chou Chu
Yin-Chung Chen
Affiliation:
Institute of Applied Mechanics, National Taiwan University, Taipei 106, Taiwan
Shih-Lin Huang
Affiliation:
Institute of Applied Mechanics, National Taiwan University, Taipei 106, Taiwan
Zi-Ya Li
Affiliation:
Institute of Applied Mechanics, National Taiwan University, Taipei 106, Taiwan
Chien-Cheng Chang*
Affiliation:
Institute of Applied Mechanics, National Taiwan University, Taipei 106, Taiwan Center for Advanced Study in Theoretical Sciences, National Taiwan University, Taipei 106, Taiwan
Chin-Chou Chu*
Affiliation:
Institute of Applied Mechanics, National Taiwan University, Taipei 106, Taiwan
*
†Email addresses for correspondence: mechang@iam.ntu.edu.tw, chucc@iam.ntu.edu.tw
†Email addresses for correspondence: mechang@iam.ntu.edu.tw, chucc@iam.ntu.edu.tw
Get access Rights & Permissions [Opens in a new window]

Abstract

Numerical simulations and laboratory experiments were jointly conducted to investigate a bathtub vortex under the influence of a protruding cylinder in a rotating tank. In the set-up, a central drain hole is placed at the bottom of the tank and a top-down cylinder is suspended from the rigid top lid, with fluid supplied from the sidewall for mass conservation. The cylinder is protruded to produce the Taylor column effect. The flow pattern depends on the Rossby number ($\mathit{Ro}= U/ fR$), the Ekman number (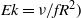$\mathit{Ek}= \nu / f{R}^{2} )$ and the height ratio, 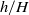$h/ H$, where 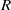$R$ is the radius of the cylinder, 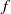$f$ is the Coriolis parameter, $\nu $ is the kinematic viscosity of the fluid, 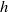$h$ is the vertical length of the cylinder and 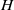$H$ is the height of the tank. It is found appropriate to choose 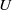$U$ to be the average inflow velocity of fluid entering the column beneath the cylinder. Steady-state solutions obtained by numerically solving the Navier–Stokes equations in the rotating frame are shown to have a good agreement with flow visualizations and particle tracking velocimetry (PTV) measurements. It is known that at 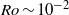$\mathit{Ro}\sim 1{0}^{- 2} $, the central downward flow surrounded by the neighbouring Ekman pumping forms a classic one-celled bathtub vortex structure when there is no protruding cylinder (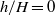$h/ H= 0$). The influence of a suspended cylinder (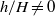$h/ H\not = 0$) leads to several findings. The bathtub vortex exhibits an interesting two-celled structure with an inner Ekman pumping (EP) and an outer up-drafting motion, termed Taylor upwelling (TU). The two regions of up-drafting motion are separated by a notable finite-thickness structure, identified as a (thin-walled) Taylor column. The thickness 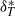${ \delta }_{T}^{\ast } $ of the Taylor column is found to be well correlated to the height ratio and the Ekman number by 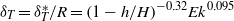${\delta }_{T} = { \delta }_{T}^{\ast } / R= {(1- h/ H)}^{- 0. 32} {\mathit{Ek}}^{0. 095} $. The Taylor column presents a barrier to the fluid flow such that the fluid from the inlet may only flow into the inner region through the narrow gaps, one above the Taylor column and one beneath it (conveniently called Ekman gaps). As a result, five types of routes along which the fluid may flow to and exit at the drain hole could be identified for the multi-celled vortex structure. Moreover, the flow rates associated with the five routes were calculated and compared to help understand the relative importance of the component flow structures. The weaker influence of the Taylor column effect on the bathtub vortex at 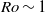$\mathit{Ro}\sim 1$ or even higher 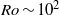$\mathit{Ro}\sim 1{0}^{2} $ is also discussed.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Rotating flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 733 , 25 October 2013 , pp. 134 - 157
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andersen, A., Bohr, T., Stenum, B., Juul Rasmussen, J. & Lautrup, B. 2003 Anatomy of a bathtub vortex. Phys. Rev. Lett. 91, 104502.Google Scholar
Andersen, A., Bohr, T., Stenum, B., Juul Rasmussen, J. & Lautrup, B. 2006 The bathtub vortex in a rotating container. J. Fluid Mech. 556, 121–146.Google Scholar
Andersen, A., Lautrup, B. & Bohr, T. 2003 An averaging method for nonlinear laminar Ekman layers. J. Fluid Mech. 487, 81–90.Google Scholar
Bellamy-Knights, P. G. 1970 An unsteady two-celled vortex solution of the Navier–Stokes equations. J. Fluid Mech. 41, 673–687.Google Scholar
Bøhling, L., Andersen, A. & Fabre, D. 2010 Structure of a steady drain-hole vortex in a viscous fluid. J. Fluid Mech. 656, 177–188.Google Scholar
Boyer, D. L. & Davies, P. A. 2000 Laboratory studies of orographic effects in rotating and stratified flows. Annu. Rev. Fluid Mech. 32, 165–202.Google Scholar
Burgers, J. M. 1948 A mathematical model illustrating the theory of turbulence. Adv. Appl. Mech. 1, 171–199.CrossRefGoogle Scholar
Cushman-Roisin, B. & Beckers, J. M. 2007 Introduction to Geophysical Fluid Dynamics: Physical and Numerical Aspects. Academic Press.Google Scholar
Echávez, G. & McCann, E. 2002 An experimental study on the free surface vertical vortex. Exp. Fluids 33, 414–421.Google Scholar
Foster, M. R. 1972 The flow caused by the differential rotation of a right circular cylindrical depression in one of two rapidly rotating parallel planes. J. Fluid Mech. 53, 647–655.Google Scholar
Greenspan, H. P. & Howard, L. N. 1963 On a time-dependent motion of a rotating fluid. J. Fluid Mech. 17, 385–404.Google Scholar
van Heijst, G. J. F. 1994 Topography effects on vortices in a rotating fluid. Meccanica 29, 431–451.Google Scholar
Hide, R. 1968 On source–sink flows in a rotating fluid. J. Fluid Mech. 32, 737–764.Google Scholar
Hide, R. & Ibbetson, A. 1968 On slow transverse flow past obstacles in a rapidly rotating fluid (with the appendix by Lighthill, M. J.). J. Fluid Mech. 32, 251–272.Google Scholar
Huang, S. L., Chen, H. C., Chu, C. C. & Chang, C. C. 2008 On the transition process of a swirling vortex generated in a rotating tank. Exp. Fluids 45, 267–282.Google Scholar
Ingersoll, A. P. 1969 Inertial Taylor columns and Jupiter’s great red spot. J. Atmos. Sci. 26, 744–752.Google Scholar
Jacobs, S. J. 1964 The Taylor column problem. J. Fluid Mech. 20, 581–591.Google Scholar
Lugt, H. J. 1996 Introduction to Vortex Theory. Vortex Flow Press.Google Scholar
Lundgren, T. S. 1985 The vortical flow above the drain-hole in a rotating vessel. J. Fluid Mech. 155, 381–412.CrossRefGoogle Scholar
Martin, S. & Drucker, R. 1997 The effect of possible Taylor columns on the summer ice retreat in the Chukchi Sea. J. Geophys. Res. 102, 10473–10482.Google Scholar
Moore, D. W. & Saffman, P. G. 1969 The structure of free vertical shear layers in a rotating fluid and the motion produced by a slowly rising body. Proc. R. Soc. Lond. A 264, 597–634.Google Scholar
Noguchi, T., Yukimoto, S., Kimura, R. & Niino, H. 2003 Structure and instability of sink vortex. Proceedings of PSFVIP-4, F4080. (http://psfvip4.univ-fcomte.fr/Fpsfvip4/).Google Scholar
Owen, J. M., Pincombe, J. R. & Rogers, R. H. 1985 Source–sink flow inside a rotating cylindrical cavity. J. Fluid Mech. 155, 233–265.Google Scholar
Pedlosky, J. 1987 Geophysical Fluid Dynamics, 2nd edn. Springer.Google Scholar
Proudman, J. 1916 On the motion of solids in a liquid possessing vorticity. Proc. R. Soc. Lond. A 92, 408–424.Google Scholar
Stepanyants, Y. A. & Yeoh, G. H. 2008 Stationary bathtub vortices and a critical regime of liquid discharge. J. Fluid Mech. 604, 77–98.Google Scholar
Stewartson, K. 1957 On almost rigid rotations. J. Fluid Mech. 3, 17–26.CrossRefGoogle Scholar
Stewartson, K. 1966 On almost rigid rotations. Part 2. J. Fluid Mech. 26, 131–144.Google Scholar
Sullivan, R. D. 1959 A two-cell vortex solution of the Navier–Stokes equations. J. Aerosp. Sci. 26, 767–768.Google Scholar
Taylor, G. I. 1923 Experiments on the motion of solid bodies in rotating fluids. Proc. R. Soc. Lond. A 104, 213–218.Google Scholar
Yukimoto, S., Niino, H., Noguchi, T., Kimura, R. & Moulin, F. Y. 2010 Structure of a bathtub vortex: importance of the bottom boundary layer. Theor. Comput. Fluid Dyn. 24, 323–327.Google Scholar