In the mid-1840s, Britain was taken over by a “railway mania.” More than 1,200 railway projects were registered in 1845 alone, and this mania resulted in an unprecedented expansion of the British railway network, which formed the basis of the railway system that endured into the twentieth century (Dyos and Aldcroft Reference Dyos and Aldcroft1969; Campbell and Turner Reference Campbell and Turner2015; Casson Reference Casson2009).
Even though incorporation had been liberalized by the Joint Stock Companies Act of 1844, railway companies still had to petition Parliament for a Private Act allowing them to begin construction of their intended lines. More than seven hundred companies did so at the height of the mania between 1844 and 1845. The House of Commons screened
the applications and approved roughly half (51 percent of the companies applying for an act in 1844 and 49 percent in 1845).Footnote 1
How did Parliament choose railway bills? Given the importance of this regulatory process for the subsequent British transport network, it is surprising that this question has so far received scant attention. It is particularly puzzling, as the modern scholarly consensus tends towards the view that Parliament approved too many railways resulting in an inefficient network (Campbell and Turner Reference Campbell and Turner2015; Casson Reference Casson2009; Odlyzko Reference Odlyzko2016). For instance, Mark Casson estimates that “equivalent social benefits could have been obtained with only 13,000 miles of track” rather than the approximately 20,000 miles that were built (Casson Reference Casson2009, p. 2).
An early case of a technology bubble, the railway mania absorbed large sums from hopeful investors, including MPs. MPs faced additional political pressure from their constituents, many of whom were investors in local railway projects. In addition, securing a connection to the new transportation network was perceived to be crucial for local development (Casson Reference Casson2009). Either motivated by the protection of private rents or by developmental ideals, MPs were bound to have an interest in at least some of the companies applying to Parliament. In this paper, we test whether MPs’ choices were swayed by private interests or constituency pressure.
Our study of the role of MP’s interests in regulating the emerging British railway network speaks to a growing literature on the “new” corruption of British politicians in the nineteenth century, focused in particular on politician-firm connections (Bogart Reference Bogart2018; Braggion and Moore Reference Braggion and Moore2013; Burhop, Chambers, and Cheffins Reference Burhop, Chambers and Cheffins2014; Grossman and Imai Reference Grossman and Imai2016; Kuo Reference Kuo2018). Whereas the eighteenth century was characterized by an “Old Corruption,” in which state funds were funneled to political clients (Harling Reference Harling1996; Rubinstein Reference Rubinstein1983), the growing industrial economy of the nineteenth century gave scope to politicians to supplement their incomes through the allocation of property rights favoring new industries (Bogart and Richardson Reference Bogart and Richardson2011; Harris Reference Harris2000; Hoppit Reference Hoppit2011). The case we focus on here speaks to this and points towards new forms of rent-seeking ushered in by the coming of the steam age.
The fear that personal interests might determine which projects got approved was not lost on contemporaries. In an effort to insulate the process of parliamentary scrutiny from vested interests, Parliament itself amended its standing orders to prevent MPs from voting on projects in which they were interested. Despite its good intentions, this set-up did not exclude all the possibilities for strategic voting since MPs could agree to vote for each others’ interests. Consequently, we focus on identifying instances of vote trading (logrolling) among MPs.
Logrolling has long attracted interest in formal political theory and public choice. Models in this tradition have investigated the individual rationality of politicians engaged in vote trading, as well as the externalities deriving from it. The first seminal contribution was due to Buchanan and Tullock (Reference Buchanan and Tullock1965), who considered logrolling to be welfare-enhancing, in particular, because it protected the interests of minorities. Riker and Brams (Reference Riker and Brams1973) later argued that even if mutually advantageous, vote trades generate externalities to the parties not involved in the trades. They further showed that, in aggregate, vote trading harms everybody, including the traders, a result they called the “paradox of vote trading.”Footnote 2 As a vehicle for government interference in the economy for private gain, logrolling is also a prime example of rent-seeking, the concept introduced around the same time by Krueger (Reference Krueger1974).
If the welfare implications of logrolling are not settled, testing for its presence is also notoriously difficult. In the absence of direct evidence on vote trades, researchers have resorted to inferring their presence from particular voting patterns. This is not easy for two main reasons. First, there is an indeterminacy in interpreting a politician’s vote, which may reflect their preferences or a trade (Clinton and Meirowitz Reference Clinton2004). Second, the set of possible trades may not be well defined. Politicians can enter into a form of implicit collusion where they vote for the interests of others in expectation of compensation in the future whenever a project they are interested in comes up for a vote. In addition, bills often embed multiple issues, making it difficult to disentangle what is being voted for, and because legislators can have many political priorities, it is not always clear in what manner they have been politically “repaid."Footnote 3 In consequence, although legislative histories and qualitative studies are rich in examples, it is difficult to measure the prevalence of logrolling.
Against this background, the peculiarities of the British Parliament’s standing orders offer an ideal setting to evaluate the extent of legislative logrolling. First of all, Parliament assigned groups of companies to committees of disinterested MPs who decided which companies in their group to approve. The upshot of this was that not all MPs could vote for all projects, which provides us with a control group to test the impact of logrolling—the MPs who were not in a position to trade votes. A second problem in estimating the impact of strategic voting is the fact that opportunities to logroll are not usually allocated randomly but created by MPs themselves. However, we will show that MPs could not have foreseen their ability to trade votes in advance of establishing an interest in particular railway companies. Since MPs did not know which committee they would be assigned to at the time they established their interests, they could not have picked companies to maximize their ability to trade votes, thus avoiding the important problem of endogenous network formation. A third concern is that not all historical interests are observable to the researcher today. We explore the impact of unobserved interests by simulating their effects. Our simulations demonstrate that omitted interests bias the measurement of logrolling towards zero. Our findings should therefore be read as a lower bound of the true logrolling effect.
Our methodological approach rests on social network analysis and the econometrics of peer effects. We start by mapping politicians’ preferences to bills and then exploit exogenous institutional restrictions on which politicians were allowed to vote for which bills in order to identify a set of feasible vote trades. This allows us to infer whether trading occurred by testing for endogenous effects (in the sense of Manski 1993) in the voting for railway projects within the network of potential trades.
Our research design follows an already existing empirical literature on logrolling (Stratmann Reference Stratmann1992, Reference Stratmann1995; Irwin and Kroszner Reference Irwin and Kroszner1996; Kardasheva Reference Kardasheva2013; Aksoy Reference Aksoy2012; Cohen and Malloy Reference Cohen and Malloy2014). The earliest statistical framework was laid out by Stratmann (Reference Stratmann1992), who used the predicted votes of a potential interest group to test for the presence of a trade within a linear vote model.Footnote 4 Stratmann’s approach requires a valid method to pre-specify the set of possible vote trades—a problem he anticipated, noting that “the possible combinations [of vote trades] are nearly boundless, and the task of identifying which clusters of issues are involved in a logroll could be daunting” (Stratmann Reference Stratmann1992, p. 1164). Moreover, Stratmann’s approach is limited to considering dyadic trades.Footnote 5 Because we consider a context in which politicians were restricted as to the projects they could vote for, the possible combinations of vote trades are strongly bounded, and we can test all possible vote-trades simultaneously. We do so by encoding vote-trades in a social network, thus making our approach to testing for logrolling equivalent to a peer-effects estimator.Footnote 6
Our estimates show that MPs made use of their opportunities to trade and that this resulted in a substantial increase in the number of railway companies that were approved. We estimate that logrolling in Parliament increased the number of approved railways by one-quarter relative to a situation without vote trading. Furthermore, we document a negative selection from logrolling. Companies that could be approved by trading votes ended up having lower market values than their peers. The aggregate loss for investors was substantial, ranging from 1/3 to 1 percent of contemporary GDP.
The paper is organized as follows. The next section introduces the historical context. We focus on the nature of the institutions created by the British Parliament to approve Private Railway Bills and how that institutional structure enables us to identify logrolling. We follow this with a description of methods to detect feasible opportunities for logrolling as well as the data, which we compiled from a variety of nineteenth-century sources. The next section sets up the estimation and reports our results and is followed by a section collecting a number of robustness checks designed to interrogate the validity of our research design. In a final section, we test whether logrolling was beneficial—by promoting gains from trade—or detrimental—by providing gains to the few while passing on the costs to the many. We offer a partial answer to this question by evaluating how the companies approved through logrolling fared in the stock market in relation to their peers. Our results suggest that, at least in this case, logrolling involved a negative externality, as the companies involved were less valuable, on average. A conclusion rounds up the paper.
THE PARLIAMENTARY APPROVAL OF RAILWAY BILLS IN THE MID-NINETEENTH CENTURY
The years 1844 and 1845 saw the explosion of speculative activity in joint-stock railway companies (Pollins Reference Pollins1954; Odlyzko Reference Odlyzko2010; Evans Reference Evans1849; Dyos and Aldcroft Reference Dyos and Aldcroft1969; Casson Reference Casson2009; Campbell Reference Campbell2013; Campbell and Turner Reference Campbell and Turner2012). Encouraged by low interest rates and the new Companies Act of 1844, which simplified the registration and promotion of joint-stock companies, interest in railway equities boomed, and the creation of new railway companies rose in tandem.
Registering and promoting railway companies was a relatively simple affair, but building the line was more tightly regulated. Unlike a regular joint-stock company, railway companies required Acts of Parliament in order to begin construction on the line (Williams Reference Williams1949). The mania for railway speculation was so pronounced that Parliament was overrun with applications from railway companies. In the two parliamentary sessions of 1845 and 1846, there were almost 720 applications for railway bills. Figure 1 shows the mileage of new railway lines authorized by Parliament annually, and the anomalous impact of 1845 and 1846 is apparent. Moreover, this is merely the length of line authorized; the total applied for was easily double the amount approved.

Figure 1. ANNUAL MILEAGE OF NEW RAILWAY LINES AUTHORIZED BY PARLIAMENT
Source: FRED, series A0284DGBA374NNBR.
The extent of the promotional activity implied an enormous amount of work for individual MPs, who were required to hear evidence on each line seeking parliamentary authorization. In 1844 Parliament formed a Select Committee, chaired by Gladstone, the future Liberal prime minister, to recommend a solution to cope with this “crush of business.” After some debate, Parliament decided to set aside its standing orders for private bills (which involved a discussion and vote by the whole House for each bill) and experiment with a new method.Footnote 7
The new standing orders were structured around the principles of avoiding conflicts of interest and considering competing schemes together. These were not uncontroversial choices, and during the 1830s many had argued that local MPs should oversee bills that affected their constituents because they had a duty to represent their interests and also on the grounds that they possessed useful “local knowledge” (Williams Reference Williams1949). However, by 1840 feeling had tilted towards the view that the conflicts of interest outweighed the value of local knowledge, such that private bills should only be presented to committees of disinterested members.Footnote 8 Contemporaries now feared that Parliament would be captured by venal influence. Even the Prime Minister, Robert Peel, echoed these concerns in a letter to the then President of the Board of Trade, Lord Dalhousie: “I saw before me the results of active canvass by powerful companies … members [of parliament], few of whom had read a word of the evidence … were prepared to vote on other considerations than those of the merits of the questions."Footnote 9
Next to corruption, the British government also worried about inefficiency, that is, that under local political pressure Parliament might approve a far greater number of railway schemes than what would be economically rational.Footnote 10 Peel again shared his concerns with Parliament, stating that “the severe competition which would be created by the great and extraordinary demand for labour, and the great rise of prices which the application of such an amount of capital would occasion” made him doubt “whether it would be for the public benefit that so extraordinary a demand for railways should be encouraged, or that such an enormous application of capital to one branch of enterprise, diverting it from all others, should be sanctioned by Parliament."Footnote 11
The precise mechanics of the committee system were laid out in 1844 by Gladstone’s report on Railway Bills and the Standing Orders.Footnote 12 In the new standing orders, a Select Committee on Railway Bills Classification grouped railway schemes that competed against each other or with existing railways. Each group of projects would then go to a five-member subcommittee that decided which schemes to approve (Williams Reference Williams1949). In the parliamentary session of 1845 there were 46 active subcommittees deciding on 210 railway bill applications; in the 1846 session 67 subcommittees scrutinized 508 railway bills. These numbers do not exhaust the universe of railway promotions, as many provisionally registered companies ended up not applying to Parliament (Geisler Mesevage Reference Geisler Mesevage2016).
The main function of each subcommittee was to hear evidence from the promoters in support of their bill, as well as from engineers and from locals claiming that their region would benefit from improved railroad communication. It also heard evidence from the railway’s opponents.Footnote 13 Most of the filtering of railway bills occurred at this stage. The process ended in the Commons with a vote in the full House, but practically all recommendations from the subcommittees were rubber-stamped by the House.Footnote 14
Despite the innovative standing orders, the time elapsed between starting a railway project and seeing it approved by Parliament was very long. In the first step, typically occurring up to a year before the application to Parliament, railway companies acquired subscribers for their shares and plotted their proposed route. Companies then had to apply to Parliament by 30 November in order to have their application considered in the parliamentary session in the Spring of the following year. At the time of their application, railways submitted the plans of their proposed route and a list of the subscribers for their shares. These applications were then sorted by the Select Committee on Railway Bill Classification, which grouped the railways and assigned MPs to the subcommittees. As a consequence of this sequencing, the route the railway would ultimately take and the railway’s initial investors were fixed prior to the assignment of railways to committees. All groups of railways were then evaluated in parallel—as the subcommittees sat up until they had decided on all the railways in their group. The date at which a decision would be rendered on any given line could not be predicted a priori as it depended on the degree of opposition faced by each line and the time it took to gather evidence for and against it. To give an indication, in 1845 the median committee sat for eight working days, or about two weeks given the working schedule of MPs, and the average committee sat for about 12.5 days.Footnote 15
This time sequence is important for our identification strategy of the causal effect of logrolling opportunities on the approval of railways by Parliament. It is hard to imagine how MP interests (particularly which companies they invested in) could be endogenously fixed in anticipation of the unknown assignment of MPs to subcommittees more than a year later. In other words, the long lags between the creation of vested interests and the process of Parliamentary approval establish a plausible case for the exogeneity of the logrolling opportunities in Parliament.
The key element in Gladstone’s report was a rule to select the MPs who would sit in each subcommittee. MPs were barred from sitting on a subcommittee if that would entail them overseeing a railway in which they held an interest. Interest was understood as the pressure from local constituents or personal pecuniary investments, with the parliamentary motion stipulating that committee members had to “sign a declaration that their constituents have no local interest, and that they themselves have no personal interest, in the Bill or Bills referred to them."Footnote 16
Rather than taking the honorable members’ word for it, Parliament checked that both personal and local interests did not contaminate the composition of subcommittees, as we describe later.Footnote 17 Given the institutional bulwarks designed specifically to hold back the push of “sinister interests,” it is no wonder that modern historians have conjectured that logrolling must have played a prominent role in explaining the suspected interference by vested interests. Mark Casson states that “in a classic logrolling manoeuvre, they [MPs] collectively protected their local reputations as champions of the local railway schemes in order to safeguard their electoral popularity” (Casson Reference Casson2009, p. 18).
The views of historians also reflect the suspicions of contemporaries. Writing in 1847, The Sun described the system neatly, noting that “the Member for Yorkshire might be appointed to consider a bill connected with Cornwall, and the Member for Cornwall might, on the other hand, be selected to adjudicate on the Bill relating to Yorkshire. The two Hon. Members, therefore, were those placed in a position to influence the decision of each other, and by means of a mutual understanding between two, the views and wishes of the circumstances of Yorkshire and Cornwall were carried into effect."Footnote 18 It is this setting that forms the basis for our investigation into logrolling in the nineteenth-century British Parliament. In the next section, we discuss methods to encode the opportunities for parliamentarians to engage in logrolling.
LOGROLLING: A SOCIAL NETWORK APPROACH
General Problem
The historical context we have described creates an interesting setting for the study of logrolling. To see this, it is helpful to start by considering the problem in a more abstract framework. The characteristic feature of a logroll is that each actor’s payoffs depend on other actors’ cooperation. Settings in which an actor’s outcomes depend on the choices of others arise frequently in the microeconomics of social interactions among groups of actors. Not mediated by prices, the influence of a peer group can be justified by mechanisms such as conformity, imitation, or interdependent preferences. Whereas, in the first two cases, peer effects are conveyed as externalities from the group to the individual, in the last case individual utility depends on “joint effort” in the sense that actions are strategic complements.Footnote 19
Blume et al. (Reference Blume, Brock, Durlauf and Jayaraman2015) derive the micro foundations for peer-effects models arising from the economics of social interactions. In a setting where utility is concave on other actors’ moves, first-order conditions yield linear strategy profiles that depend on peer choices.Footnote 20 In our case, in the presence of logrolling, the likelihood of an MP getting his project approved depended on him trading votes with his peers. Since votes determined outcomes (railways approvals), we expect to find a positive affiliation between an MP’s outcome and the outcomes of his peers, the MPs with whom he could trade. First, however, we need to clarify who these peers were and why the set of trades is well-described by a social network.
We begin with a set of companies, which we denote C. We also have a set of politicians, P. There are two sorts of relationships that can form between any c in C and ρ in P: relationships of vested interest and relationships of oversight. These two kinds of relationships define two matrices. First, there is an oversight matrix O of dimensions ρ x C such that the p, cth entry is one if ρ oversees the approval of c and zero otherwise. Likewise, we define the vested interest matrix V of dimensions ρ x C, where the p, cth entry is equal to one if politician ρ is interested in company c and zero otherwise. It should be clear that ρ is not the total number of MPs in session, but only of those selected for a railway committee. Some of these MPs might not have an interest in any of the projects under consideration.Footnote 21 ρ also does not include all the MPs with an interest on one or more lines, since many were not selected for a committee and, hence, had no opportunity to logroll.
Our matrices of relationships can be combined to reveal logrolling opportunities. Following the use of affiliation graphs in social network analysis, we can compute an adjacency matrix:
where
![]() $$V'$$
is the transpose of the interest matrix V. This yields a ρ x ρ matrix that has the property that the value of the i, jth entry denotes the number of railways that politician i oversees and in which politician j is interested.Footnote 22
$$V'$$
is the transpose of the interest matrix V. This yields a ρ x ρ matrix that has the property that the value of the i, jth entry denotes the number of railways that politician i oversees and in which politician j is interested.Footnote 22
Given that we can graph who oversees whom, we can easily identify opportunities for logrolling: a logroll is possible between two or more politicians whenever those politicians are in a cycle in our directed graph. Thus in the simplest case, an arrow running from i to j and from j to i would depict a cycle of length two, but longer cycles also exist, which would permit the construction of more complicated trades, say from i to j to k and back to i. In practice, cycles beyond a certain length would be unlikely as trading strategies, as they would involve the coordination of too many participants. In consequence, we limit our attention to cycles up to length three.Footnote 23
We identify the individual logrolling opportunities using a graph search algorithm designed for the identification of subgraph isomorphisms.Footnote 24 The key to this transformation consists in making the connections within the cycles we identified complete: that is, if we found a cycle on the logrolling graph between MPs i, j, and k, we rewrite the matrix so that i, j, and k are all connected with multi-directional links, as opposed to a path of form
![]() $$i \to j \to k \to i$$
.Footnote 25 Thus we transform the matrix M into a new matrix A subject to
$$i \to j \to k \to i$$
.Footnote 25 Thus we transform the matrix M into a new matrix A subject to
 $$\Lambda = \left\{ {\matrix{ {1,} & {{\rm{if}}\;{M_{i,j}} \in \;{L_{i,j}}} \cr
{0,} & {otherwise} \cr } } \right.$$
$$\Lambda = \left\{ {\matrix{ {1,} & {{\rm{if}}\;{M_{i,j}} \in \;{L_{i,j}}} \cr
{0,} & {otherwise} \cr } } \right.$$
where L is the list of connections between all MPs i and j that have a logroll.
We turn in the next section to a description of the data, in particular how we measured and encoded the interests of MPs.
Data Requirements
Our research design requires three sets of data.Footnote 26 First, we need to define the oversight matrix O, which in our case is given by the allocation of MPs to subcommittees. Second, we need to measure MPs’ interests in bills in order to define the matrix V. Finally, we incorporate in the regression analysis data on exogenous controls, characterizing the MPs and their constituencies. Matrix O was coded from information in Parliamentary Papers that published a full list of the MPs sitting on each subcommittee, and the list of railways that they screened.Footnote 27 The dataset compiled by Aydelotte (Reference Aydelotte1984) for the 1841-47 House of Commons was useful for creating exogenous controls to include in the regressions.
Next, we use two sources to code MPs’ interests in railway bills. One of the functions of the railway subcommittees was evaluating the quality and geographic distribution of the railway company’s investors. Consequently, railway companies were required to submit the lists of their subscribers to Parliament.Footnote 28 From these lists, we were able to observe which MPs had direct investments in railway companies: 42 MPs in 1845 and 120 in 1846.
To be sure, these lists measure MPs’ investment interests with some noise. A first issue is that there is no guarantee that an MP who was among the initial subscribers to a company’s scrip still owned it at the time Parliament decided on the company’s fate a year later. However, even if an MP had sold his subscription contract, he remained liable for company debts until the railway was approved, at which point ownership transfers would be officially recorded by the company (Anon. 1847).Footnote 29 In consequence, even if an MP had sold, he might still have an interest in seeking the approval of a company to which he had subscribed.
A second issue is that the lists of initial subscribers are sometimes criticized for containing factually inaccurate information or information fabricated by railway companies (Campbell and Turner Reference Campbell and Turner2012). Such criticism may hold merit in general, but it is unlikely to apply to the investments of MPs in particular. Since the MPs themselves were set to
verify the lists of shareholders, companies would be foolish to pretend to possess a connection with an MP as this would be easily found out. As we will show via simulation, in the reverse case of hidden interests (if companies omitted MP investments or if MPs invested through proxies), the effect is biased downwards, so our results should be taken as conservative estimates of the impact of logrolling in Parliament.Footnote 30
The second way of defining MP interests in railway bills takes the viewpoint of their constituents. We proxy local interest in a railway project by coding whether the route of each proposed railway crossed the constituency of the MP in question. We collected information on routes from Tuck’s Railway Shareholder’s Manual, a publication that contained short descriptions of almost all projected railways, including lists of the towns they proposed to pass through (Tuck Reference Tuck1846). We geo-referenced the lists of towns and then matched the path of each railway with the shapefiles of the electoral constituencies in Great Britain as they existed in 1845.Footnote 31
For those railways without a route reported in Tuck, we used the companies’ names to approximate their route. This was possible as the convention at the time was to name railway companies after their proposed route, such as the “Direct London and Portsmouth.” This method is obviously not exact, as the actual routes could have crossed a constituency that would not have been predicted by a simple line between the terminal cities. Nevertheless, these companies account for only 12.8 percent of the railways in our sample in 1845 and 11.4 percent in 1846, and the listed towns are rarely separated by more than one constituency, so that classification errors are very unlikely.
An additional concern is that we observe the success or failure of railway projects within small committees of five MPs rather than the individual votes of the MPs forming the committees. This could lead to a misclassification error, as we infer the behavior of individual MPs from the decisions of the committees they sat on. For instance, if we observe that a railway was approved by a committee, that does not necessarily mean that one of its members behaved as we expected in a logroll situation. Conversely, if the railway was rejected, the MP could have tried to approve it but was outvoted in the committee. Parliament’s standing orders, however, minimize this concern since they only required that committees reported individual votes when decisions were divided.Footnote 32 As no railway committee reported their members’ votes that implies that decisions within the committees were reached by consensus, a situation that favored MPs lobbying on behalf of colleagues sitting in other committees.Footnote 33
As a final check of the consistency of the data, we confirmed that the matrix Min Equation (1) was hollow, meaning that the Select Committee on Railway Bills Classification successfully excluded the vested interests it could observe from the subcommittees approving railway bills. Even though the committee only had to verify two pieces of information in allocating MPs to committees (which constituency they represented and whether they were among the list of subscribers submitted by the railroad companies), it is a tribute to the efficiency and reliability of the process that no mistakes were made.
SPECIFICATION AND ESTIMATION
Specification
To operationalize our social network approach to logrolling, we estimate a peer-effects model across the network of feasible trades just described.Footnote 34 We follow the econometric literature on peer effects, in particular the statistical model discussed in Bramoulle, Djebbari, and Fortin (2009). Our model takes the form:
The dependent variable is the success rate of an individual MP i, which we measure as the fraction of projects in which he has an interest, and that got approved or
![]() $${y_i} = \;approve{d_i}/interest{s_i}$$
. and
$${y_i} = \;approve{d_i}/interest{s_i}$$
. and
![]() $${y_i} = \;0\;{\rm{when}}\;interest{s_i} = 0.$$
Footnote 35 The term Λ is the matrix defined in Equation (2), which encodes which MPs could logroll with each other. In this model, the expression ρΛy represents what Manski (1993) calls the endogenous effect, with the parameter ρ capturing the propensity of an individual’s outcome to vary with the outcomes of their peers.Footnote 36 The vector X collects a set of exogenous characteristics of the MPs and their constituencies, and i is a column vector of ones. The covariates are introduced directly via βX to test for the impact of these characteristics on each MP’s success rate. They are also included via the lagged expression
$${y_i} = \;0\;{\rm{when}}\;interest{s_i} = 0.$$
Footnote 35 The term Λ is the matrix defined in Equation (2), which encodes which MPs could logroll with each other. In this model, the expression ρΛy represents what Manski (1993) calls the endogenous effect, with the parameter ρ capturing the propensity of an individual’s outcome to vary with the outcomes of their peers.Footnote 36 The vector X collects a set of exogenous characteristics of the MPs and their constituencies, and i is a column vector of ones. The covariates are introduced directly via βX to test for the impact of these characteristics on each MP’s success rate. They are also included via the lagged expression
![]() $$\delta {M'}X$$
that captures the so-called contextual effects of the exogenous characteristics of one’s peers on one’s own outcome (where M is defined in Equation (1)). If we think of the vector of covariates X as describing an MP’s “type,” then the expression
$$\delta {M'}X$$
that captures the so-called contextual effects of the exogenous characteristics of one’s peers on one’s own outcome (where M is defined in Equation (1)). If we think of the vector of covariates X as describing an MP’s “type,” then the expression
![]() $${M'}X$$
is computing the average type in the group of MPs to whom MP i is connected through the social graph Mʹ.Footnote 37 A reason to include this term is that we might imagine MPs deciding on the projects before them by considering the identity of the MPs to whom they were connected through the network of subcommittees, even if they were not able to trade votes with them. For instance, MPs of the same party might approve projects in which they knew that their colleagues had an interest while voting down projects associated with their political rivals. Thus
$${M'}X$$
is computing the average type in the group of MPs to whom MP i is connected through the social graph Mʹ.Footnote 37 A reason to include this term is that we might imagine MPs deciding on the projects before them by considering the identity of the MPs to whom they were connected through the network of subcommittees, even if they were not able to trade votes with them. For instance, MPs of the same party might approve projects in which they knew that their colleagues had an interest while voting down projects associated with their political rivals. Thus
![]() $${X_i}$$
would be a dummy for the party identification of an MP, and
$${X_i}$$
would be a dummy for the party identification of an MP, and
![]() $$M'{X_i}$$
would compute the average party identification of the MPs approving MP i’s projects. The expression
$$M'{X_i}$$
would compute the average party identification of the MPs approving MP i’s projects. The expression
![]() $$M'{X_i}$$
. is the network “lag” of the variable
$$M'{X_i}$$
. is the network “lag” of the variable
![]() $${X_i}$$
. as it computes the values lagged one step in network space.
$${X_i}$$
. as it computes the values lagged one step in network space.
Recent literature in econometrics has demonstrated that the parameters of these models can be reliably identified (Bramoulle, Djebbari, and Fortin Reference Bramoulle, Djebbari and Fortin2009; Blume et al. Reference Blume, Brock, Durlauf and Jayaraman2015) and have provided the tools to do so (Kelejian and Prucha Reference Kelejian and Prucha1998, 2010; Lee Reference Lee2003, Reference Lee2007; Lee, Liu, and Lin Reference Lee, Liu and Lin2010). Given that the matrix describing our endogenous effect A and the matrix describing the contextual effect M are not identical, Blume et al. (Reference Blume, Brock, Durlauf and Jayaraman2015) show that we should have no difficulty identifying the parameters of our model using the generalized spatial two-stage least squares (GS2SLS) estimator adopted in Bramoulle, Djebbari, and Fortin (Reference Bramoulle, Djebbari and Fortin2009).Footnote 38 Nevertheless, the estimate of ρ can still be biased if the types of MPs who obtained logrolls differ from those that did not in a way that causes their outcomes to be correlated (“homophily”). We take up this point at length in the subsequent robustness checks.
If our identification strategy is correct, then an MP’s logrolling opportunities should be increasing in the number of interests he had and the number of projects he oversaw. In consequence, we compute all our estimates controlling for the number of interests an MP had (the number
of companies he invested in and the number of lines projected for his constituency) and the number of projects overseen by the subcommittee in which he sat.
Before showing the estimation results of Equation (3), one final note about static vs. dynamic models. We estimate the model separately for the two cross-sections corresponding to the 1845 and 1846 sessions because the specifics of Parliament’s standing orders prevented MPs from striking deals across time. First, MPs sitting in the 1845 subcommittees would not know whether companies they would invest in over that year would apply to Parliament in 1846.Footnote 39 Second, and more crucial, even if they had that information, they could not know who would be selected to sit in the 1846 subcommittees.Footnote 40 Consequently, there was no opportunity for deferred logrolling agreements across the two sessions.
Results
Table 1 shows the results of the GS2SLS model with a logrolling matrix covering cycles that include up to three participants for the year 1845. In addition to controlling for the predictors of logrolling opportunities, we also control for a variety of MP social, political, and economic characteristics.Footnote 41 Among the first, we included a categorical variable for MPs who had graduated from university and who shared membership in the Athenaeum Club. Contrary to other clubs, which were divided along party lines, the Athenaeum accepted members from both sides of the aisle (Cowell Reference Cowell1975). Consequently, we introduce it to test whether club membership could have lowered the costs of brokering trades among MPs from different political parties.Footnote 42 We introduced three proxies for political affiliation: the conventional two-party classification computed by Aydelotte (Reference Aydelotte1984), as well as dummies for “Reform MP” and “Free-trade Club Membership,” which capture political divisions not entirely spanned by the party membership. In addition, we included dummies for whether the MP had a known connection to business interests, as coded by Aydelotte, and whether the MP had specific connections to canals that were reputed to be hostile to railways. All of these covariates are also included as spatial lags, allowing us to see whether having one’s project regulated by MPs who displayed these characteristics impacted an MP’s success rate. Table 2 reproduces this specification for the year 1846. The standard errors are robust to heteroskedasticity, but we follow Bramoulle, Djebbari, and Fortin (Reference Bramoulle, Djebbari and Fortin2009) in simplifying the model by assuming that the error term does not follow a spatial process. We show that this is warranted by testing for network autocorrelation in the error term by using a Monte Carlo permutation test for Moran’s I statistic. The tables report the test statistic and associated p-value. A statistically significant test statistic would imply that the model was misspecified.
Table 1 ESTIMATES OF PEER-EFFECTS MODEL FOR 1845, LOGROLLS UP TO LENGTH THREE

Notes: Dependent variable = share of each MP’s railway interests approved. Robust standard errors in parentheses. ***p < 0.001, **p < 0.01, *p < 0.05, §p < 0.1.
Sources: See text for definition of dependent variables. Estimation by GS2SLS.
The coefficient of interest, ρ, is significant and large across all specifications—averaging 0.825 in 1845 and 0.55 in 1846. Given that coefficients in these models should not exceed one (econometrically and theoretically), the magnitude of the result is substantial. The positive and significant coefficient indicates a substantial amount of vote trading in equilibrium, but since the coefficient cannot be interpreted as a partial derivative, we defer interpretation to the next section.
The estimates of the covariates behave as expected. The number of railways projected to cross an MP’s constituency is negatively associated with their success rate, although the estimated coefficient is not always significant. This is not surprising as it signals growth in the denominator of the outcome variable.Footnote 43 MPs with known business connections were more likely to get their projects approved, but other MP characteristics are not stable across years.
The differences between the coefficients on some variables in 1845 and 1846 should not be surprising, as the investment context was markedly different between these two years. During 1845, a growing bubble in railway equities lured many investors into the share market, such that the type of MPs who were involved in railways in the session of 1846 was probably more heterogenous (Campbell and Turner Reference Campbell and Turner2010).
A final consideration has to do with the capacity of MPs to coordinate trades. Even a path length of three could have been too long to arrange in practice. To investigate this, we re-estimated the model using only logrolls of length two. The corresponding tables are in the Online Appendix 3. The estimate of ρ with logrolls of length two decreases to a range of 0.42–0.68 for 1845 and a range of 0.37–0.44 for 1846. The decline in the magnitude of the coefficients in 1845 could reflect sampling variability, or it could reflect measurement error induced by failing to model connections that were acted on. Conversely, if MPs were very sophisticated, it is possible that they coordinated trades longer than length three. In the Online Appendix 3, we re-estimated the models up to logrolls of length five. As expected, the coefficients rise in magnitude as logrolls are added while the standard errors shrink. Therefore, by focusing on length-three logrolls, we may be biasing the results down relative to the true logrolling effect.
Interpretation of ρ
Observed across specifications, there is clear evidence of logrolling, insofar as the coefficient ρ is positive and statistically distinguishable from zero. The interpretation of ρ is complicated, however, by the fact that conceptually it reflects a cooperative equilibrium between MPs, and econometrically it is nested in a network model, such that any marginal effect ripples through the social network generating feedback. To understand the economic significance of the estimates, it is helpful to start by thinking about the impact of the logrolls in terms of the passage of an additional railway company.Footnote 44
Our dependent variable is the fraction of railways approved or the number approved over the total number of railways in which an MP has an interest, approved/interest. If an MP approves one additional project, that increases his trading partner success rate, on average, by
![]() $$1/\bar I$$
railways, where
$$1/\bar I$$
railways, where
![]() $$\bar I$$
is the average number of interests among MPs connected via logrolls. However, since the logrolling relationship is reciprocal, the original MP would receive
$$\bar I$$
is the average number of interests among MPs connected via logrolls. However, since the logrolling relationship is reciprocal, the original MP would receive
![]() $$\bar I \times \rho /\bar I = \rho $$
railways in return, and his partner would then receive
$$\bar I \times \rho /\bar I = \rho $$
railways in return, and his partner would then receive
![]() $$\rho \bar I\rho /\bar I = {\rho ^2}$$
railways, and so on. As the adjacency matrix A identifies who is connected to whom in a logroll, the actual direct and indirect effects have to be weighed by the elements in A where these are non-zero. The direct effect of MP i approving one additional railway on j is thus
$$\rho \bar I\rho /\bar I = {\rho ^2}$$
railways, and so on. As the adjacency matrix A identifies who is connected to whom in a logroll, the actual direct and indirect effects have to be weighed by the elements in A where these are non-zero. The direct effect of MP i approving one additional railway on j is thus
![]() $$\rho {\lambda _{ij'}}$$
where
$$\rho {\lambda _{ij'}}$$
where
![]() $${\lambda _{i,j}}$$
. is the i, jth weight in A. The immediate feedback on i is
$${\lambda _{i,j}}$$
. is the i, jth weight in A. The immediate feedback on i is
![]() $${\rho ^2}{\lambda _{i,j}}{\lambda _{j,i}}$$
and so on.Footnote 45 Thus evaluated at the mean, the effect per logroll of MPs agreeing to trade votes is given by:
$${\rho ^2}{\lambda _{i,j}}{\lambda _{j,i}}$$
and so on.Footnote 45 Thus evaluated at the mean, the effect per logroll of MPs agreeing to trade votes is given by:
 $$\Delta = \sum\limits_{n = 0}^\infty {{{(\rho \bar \lambda )}^{2n + 1}}\bar N} = {{\rho \bar \lambda \bar N} \over {1 - {{(\rho \bar \lambda )}^2}}},$$
$$\Delta = \sum\limits_{n = 0}^\infty {{{(\rho \bar \lambda )}^{2n + 1}}\bar N} = {{\rho \bar \lambda \bar N} \over {1 - {{(\rho \bar \lambda )}^2}}},$$
where
![]() $$\bar \lambda $$
is the average weight in a logroll and
$$\bar \lambda $$
is the average weight in a logroll and
![]() $$\bar N$$
is the average size of a logroll.Footnote 46 In 1845,
$$\bar N$$
is the average size of a logroll.Footnote 46 In 1845,
![]() $$\bar \lambda $$
is 0.27 and in 1846 it is 0.16.Footnote 47 Since each railway can only be approved once, we need to avoid double-counting logrolls for the same company. Therefore, we take the number of MPs who could logroll in each year and subtract the cases of joint logrolls (for the same company) to compute how many MPs had logrolls for unique companies.Footnote 48
$$\bar \lambda $$
is 0.27 and in 1846 it is 0.16.Footnote 47 Since each railway can only be approved once, we need to avoid double-counting logrolls for the same company. Therefore, we take the number of MPs who could logroll in each year and subtract the cases of joint logrolls (for the same company) to compute how many MPs had logrolls for unique companies.Footnote 48
Since our observed data represents an equilibrium of cooperative behavior, it is more intuitive to consider the overall magnitude of the effect by taking the number of observed logrolls and computing how much larger the observed number of approved railway projects seems to be conditional on the size of the coefficient ρ and the given social network. For 1845, we count 42 unique MP logrolls and if we take the average coefficient in Table 1
![]() $$\bar \rho = 0.825$$
, the average weight
$$\bar \rho = 0.825$$
, the average weight
![]() $${\bar \lambda _{1845}} = 0.27$$
, and the average number of trading partners
$${\bar \lambda _{1845}} = 0.27$$
, and the average number of trading partners
![]() $$\bar N = 3.7$$
and apply Equation (4), we obtain
$$\bar N = 3.7$$
and apply Equation (4), we obtain
![]() $${\Delta _{1845}} \approx 0.87$$
. Multiplying through by our 42 logrolls we obtain 36.5 companies. This is approximately 34 percent of all the railways approved in 1845. Repeating the exercise for 1846 (Table 2), we obtain 67 unique MP-logrolls, which, multiplied by
$${\Delta _{1845}} \approx 0.87$$
. Multiplying through by our 42 logrolls we obtain 36.5 companies. This is approximately 34 percent of all the railways approved in 1845. Repeating the exercise for 1846 (Table 2), we obtain 67 unique MP-logrolls, which, multiplied by
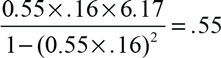 $${{0.55 \times .16 \times 6.17} \over {1 - {{(0.55 \times .\;16)}^2}}} = .55$$
, yields 36.7 additional companies, or 16 percent of all railways approved in that session. Across the two parliamentary sessions, 73 companies represent a quarter of the projects that received an act to build a line in Great Britain (excluding Ireland).
$${{0.55 \times .16 \times 6.17} \over {1 - {{(0.55 \times .\;16)}^2}}} = .55$$
, yields 36.7 additional companies, or 16 percent of all railways approved in that session. Across the two parliamentary sessions, 73 companies represent a quarter of the projects that received an act to build a line in Great Britain (excluding Ireland).
Table 2 ESTIMATES OF PEER-EFFECTS MODEL FOR 1846, LOGROLLS UP TO LENGTH THREE

Notes: Dependent variable = share of each MP’s railway interests approved. Robust standard errors in parentheses. ***p < 0.001, **p < 0.01, *p < 0.05, §p < 0.1.
Sources: See text for definition of variables. Estimation by GS2SLS.
Even though these estimates are approximate, they are clearly large and show how vote trading could be responsible for a sizable proportion of the companies approved by Parliament in the 1840s, and that persisted as an important component of the U.K. railway network well into the twentieth century. Nevertheless, the validity of interpreting these effects as a consequence of logrolling hinges on assuming that logrolling opportunities were not correlated with other unobservables that predict the outcomes of MPs—an assumption we interrogate in the next section.
ROBUSTNESS CHECKS
In this section, we consider threats to identification that stem from the difficulty of inferring the presence of logrolling from voting patterns. There are several alternative mechanisms that could lead to observation-ally equivalent estimates of ρ without involving logrolling between MPs.
First, it is possible that the reason why companies were approved depended on the characteristics of the companies more than on the characteristics of the MPs. In our specification, we can include a number of controls for MPs’ characteristics and their constituencies, but information on the merits of the projects themselves is scarce. In the first robustness check in this section, we explore the only source available on the quality of railway projects and confirm that the pattern of approved railways was not driven by this observable quality measure.
Although company quality is a missing variable, it is unlikely to be problematic unless it is correlated with patterns of connections on the network. Since our interest centers on the network autocorrelation parameter, the form of omitted variable bias that would be most likely to damage our estimates would be if linked individuals on the network were unusually similar—a problem referred to in the social networks literature as homophily. This pattern of linkage might arise if the procedural rules by which Parliament constituted the subcommittees were gamed so as to ensure that friendly MPs could trade. In the second part of this section, we test whether the voting network formed by the committees was endogenously formed, which would vitiate our identification
of the effect of logrolling. We find no evidence of endogenous network formation.
A third consideration is that the set of possible trades may not be well defined. Up to now, we have been assuming that MPs traded votes on railway projects, while they could well trade votes on different legislative processes, for instance, a vote on a railway in exchange for a vote on free trade in corn. We cannot investigate all the bills before Parliament around the time of railway approval, but we can simulate the effect of omitting ties between MPs that we cannot observe. In the third part of the section, we show that unobserved ties create an attenuation bias.
Omitted Variable Bias
As we estimate the regressions at the MP level, we do not control directly for the underlying quality of the railway projects that MPs were asked to consider. This can conceivably introduce an omitted variable bias and, under certain scenarios, lead to our method capturing spurious evidence of logrolling. If the quality of projects was publicly observable, MPs could have used that knowledge to invest only in the best companies and, if they also only approved companies above a quality threshold, it is possible that Regression (3) returned a significant estimate of p, despite the fact that no vote trading was afoot.Footnote 49 A problem with controlling for this possibility is that there is no objective measure of the viability and expected return of the railway projects that we can include in the statistical analysis. Apart from their lists of promoters and subscribers and their intended route, railway companies submitted very little information about the underlying quality of their projects. The adversarial nature of approval by a subcommittee considering competing projects together was precisely designed to allow MPs to hear opposing views on the merits of the several projects as if they were a jury in a court of law. Unlike courts, however, the railway subcommittees did not publish the reasoning behind their decisions.
Nonetheless, this lack of information can be circumvented for the 1845 session, when the railway department of the Board of Trade was called to produce an individual recommendation for each railway project, advising MPs whether to vote for or against it (Parris Reference Parris1965; Casson Reference Casson2009). The recommendations were the considered opinion of the department’s engineers, who had poured over the technical and economic evidence to judge which projects held greater promise (Parris Reference Parris1965). MPs rebelled against what they viewed as a heavy-handed intervention by the government, forcing the government to back down and admit that the recommendations from the Board of Trade were merely suggestions. A consequence of this retreat was that the railway department did not issue recommendations for the following session. Nevertheless, this is as good a measure of the quality of the projects screened in the 1845 session as we can get. This evidence can effectively be used as a placebo test for our research design. If our results were spurious, merely reflecting MPs rubber-stamping the recommendations of the Board of Trade, then we should find significant evidence of logrolling when we use the recommendations as our dependent variable. Alternatively, we include the Board of Trade recommendations as a new control variable. We implement both approaches in the Online Appendix 4 and do not find them to change the tenor of the results.Footnote 50
Endogenous Network Formation
Inferring causality from the characteristics of individuals linked via a social network is a fundamentally difficult problem due to the “generic confounding” of homophily and contagion (Shalizi and Thomas Reference Shalizi and Thomas2011). Our study is a “contagion” style model, insofar as we argue that the existence of a link on a graph (a logroll) can exert a causal impact on outcomes associated with the individuals joined through it—specifically, we suspect them of entering into unobserved compacts to aid each other. A potential confounder arises if the existence of the link itself is due to some characteristic of the MPs. A “homophily” argument would postulate that the probability of being linked is the product of some other common characteristic of the MPs that by itself may then account for the association of their outcomes. In a more familiar language, some latent variables may be generating both linkage and outcomes.
We have been interpreting the results of the peer-effects models as evidence of the strategic behavior of parliamentarians because the design of the subcommittees constituted a sort of natural experiment—assigning logrolls to MPs accidentally, such that there would not be a latent factor driving both acquiring a logroll and experiencing a favorable outcome. In this section, we interrogate that claim by considering ways in which it could be falsified and then testing to see if it can be sustained. We will consider violations of the research design in two broad categories: whether MPs could arrange to be appointed to subcommittees so as to trade with
their friends; and whether there was a filtering process whereby MPs with interests in railway companies ensured they at least got committee assignments thus suggesting that the Select Committee could be influenced by vested interests. We will take these problems in turn, beginning with the problem that would be most problematic for the research design.
The most obvious way in which the random assignment of logrolls to MPs can be violated is if MPs can maneuver to place sympathetic friends in positions to logroll with them. This might occur if MPs anticipated the benefits that could be obtained from a logroll, perceive the distribution of their colleagues’ interests, and lobby the Select Committee in charge of allocating committee assignments so as to obtain a posting that would grant them a logroll. This would be the most problematic form of endogenous logroll formation from a statistical viewpoint as it would necessarily entail the creation of logrolls between MPs who were similar in other ways—in other words, the social network would display homophily. Ex ante this seems unlikely, both because arranging to have the right people placed in the correct subcommittee would be difficult, but also because if an MP was intent on having a colleague vote in his favor, there were less complicated ways to achieve it, for instance, side payments.
Nevertheless, we will evaluate the game-ability of the committee assignment mechanism by testing whether MPs got logrolls with other MPs that were more likely to be sympathetic to them (“placing friends in the right places”). This mechanism can be evaluated with a network balance test. Given some MP characteristic
![]() $${x_i}$$
, we can test for random assignment by seeing whether the coefficient β in the regression
$${x_i}$$
, we can test for random assignment by seeing whether the coefficient β in the regression
![]() $${x_i} = \alpha + \beta \Lambda {x_i} + \varepsilon $$
is equal to zero. Since this is a simple bivariate regression we cannot employ the GS2SLS approach used in the main estimation. It is well-known that in this context the OLS estimate of β is subject to contradictory biases. On the one hand, it will be biased upwards due to reflection bias (Manski 1993). This bias comes from the fact that if i influences j, then j will have a feedback on i, generating a multiplier effect. On the other hand, the estimate of β will be biased downwards due to an “exclusion bias”: a mechanical negative correlation between an outcome and the mean of that outcome within a social network that can arise in naive OLS estimates. Caeyers and Fafchamps (Reference Caeyers and Fafchamps2016) provide a method for conducting a balance test on network data that corrects for both of these biases. Their method involves randomly permu-tating the elements in the social network in question N times, generating N random counterfactual networks, and estimating the parameter of interest in each case. This bootstrapping procedure allows characterizing the distribution of the estimator when the true network autocorrelation is zero.
$${x_i} = \alpha + \beta \Lambda {x_i} + \varepsilon $$
is equal to zero. Since this is a simple bivariate regression we cannot employ the GS2SLS approach used in the main estimation. It is well-known that in this context the OLS estimate of β is subject to contradictory biases. On the one hand, it will be biased upwards due to reflection bias (Manski 1993). This bias comes from the fact that if i influences j, then j will have a feedback on i, generating a multiplier effect. On the other hand, the estimate of β will be biased downwards due to an “exclusion bias”: a mechanical negative correlation between an outcome and the mean of that outcome within a social network that can arise in naive OLS estimates. Caeyers and Fafchamps (Reference Caeyers and Fafchamps2016) provide a method for conducting a balance test on network data that corrects for both of these biases. Their method involves randomly permu-tating the elements in the social network in question N times, generating N random counterfactual networks, and estimating the parameter of interest in each case. This bootstrapping procedure allows characterizing the distribution of the estimator when the true network autocorrelation is zero.
Table 3 shows the network autocorrelation coefficient β from bivar-iate network peer-effects regressions for each covariate in our sample, as well as the bootstrapped mean and standard deviation of the same parameter and a two-sided p-value computed using the network randomization inference procedure of Caeyers and Fafchamps (Reference Caeyers and Fafchamps2016).Footnote 51 The network autocorrelation coefficient is insignificant for all the variables. This suggests that of the things that we can measure about MPs, nothing appears to drive the correlation in outcomes estimated in the main model.
Table 3 NETWORK BALANCE TESTS OF NON-RANDOM LOGROLL ASSIGNMENT

Notes: For each variable ² is the estimate of the model ![]() $${x_i} = \alpha + \beta \;\Lambda \;{x_j} + \varepsilon .\;{\bar \beta _{mull}}$$ is the bootstrapped mean of the same coefficient from 500 random permutations of the network matrix Λ.
$${x_i} = \alpha + \beta \;\Lambda \;{x_j} + \varepsilon .\;{\bar \beta _{mull}}$$ is the bootstrapped mean of the same coefficient from 500 random permutations of the network matrix Λ.
Sources: See text for definition of variables. Authors estimations by GS2SLS and simulation.
The second potential violation of random network assignment comes from the fact that an MP could only receive a logrolling opportunity if he got to sit on a subcommittee. Not all MPs were assigned to committees, and if only MPs with vested interests in railway companies were assigned to committees, that would constitute evidence that they lobbied the Selection Committee to acquire a logrolling opportunity. We can evaluate this by simply looking at differences in the characteristics of MPs that did and did not receive committee assignments. We anticipate that there were some differences, as some members of Parliament were barely active and would not likely be tapped for membership of a subcommittee.
Table 4 MEANS AND P-VALUES FOR MPS IN AND OUT OF COMMITTEES

Sources: Authors’ calculations. See text for description of variables.
The most important variables to compare between MPs are the number of railways they invested in and the number of railways that were projected to be built in their constituency. We can see from Table 4 that there is no statistical difference in the value of these covariates for MPs that did and did not receive committee assignments. Aydelotte (Reference Aydelotte1984)’s measure of whether an MP was active in business is significant, but the mean is higher for MPs who did not obtain committee assignments. We suspect this reflects the Select Committee’s interest in screening out those with potentially conflicting interests. In addition, the MPs selected to sit on railway subcommittees had slightly higher average education, and the difference is statistically significant. It is not clear, however, how this would invalidate our identification strategy.
Taken together, our interrogation of the assignment of MPs to committees and of the similarities between MPs on committees are consistent with our identification strategy. There is no evidence of strategic maneuvering to obtain a logroll, and thus no evidence that the logrolling network itself—our matrix A—is endogenously formed. Thus it would appear that when the opportunity to trade votes presented itself, MPs availed themselves of it, but that they were not able or motivated to manipulate the system in order to acquire logrolling opportunities in the first place.
Unobserved Interests
We evaluate the measurement error problem of unobserved interests by using Monte Carlo simulations of network data for which the parameter of interest ρ is known and then estimating the value of ρ after we randomly delete interests from the social network graph.

Figure 2 DISTRIBUTION OF ![]() $${\hat \rho _{bs}}$$ AT DIFFERENT RATES OF UNOBSERVED LINKS
$${\hat \rho _{bs}}$$ AT DIFFERENT RATES OF UNOBSERVED LINKS
Source: Authors’ simulations.
We begin with a graph of 500 observations and set ρ equal to 0.7. We create a social network graph A with density 0.005 and M with density 0.01.Footnote 52 We also generate a matrix of covariates X and draw a vector of errors e from a standard normal distribution. We generate our outcome variable y from the formula
We then randomly delete a certain percentage of connections in the Λ matrix and compute ![]() $${\hat \rho _{bs}}$$, which is an estimate of the value of ρ using a GS2SLS estimator. For each percentage of links that we delete, we re-estimate
$${\hat \rho _{bs}}$$, which is an estimate of the value of ρ using a GS2SLS estimator. For each percentage of links that we delete, we re-estimate ![]() $${\hat \rho _{bs}}$$ 500 times. Figure 2 shows the distribution of our bootstrapped estimates of ρ for different percentages of randomly deleted links. It is clear that the median of the distributions shifts toward zero as the number of unobserved links increases. Nevertheless, even with significant missingness (over 30 percent), the estimate remains correctly signed. This supports the hypothesis that the impact of unobserved interests will be to induce attenuation bias of our coefficient estimates.
$${\hat \rho _{bs}}$$ 500 times. Figure 2 shows the distribution of our bootstrapped estimates of ρ for different percentages of randomly deleted links. It is clear that the median of the distributions shifts toward zero as the number of unobserved links increases. Nevertheless, even with significant missingness (over 30 percent), the estimate remains correctly signed. This supports the hypothesis that the impact of unobserved interests will be to induce attenuation bias of our coefficient estimates.
ASSESSING THE CONSEQUENCES OF LOGROLLING
In this section, we try to quantify the social consequences of logrolling. The theoretical debate has been split as to whether logrolling improves welfare (gains from trade) or harms it by allowing concentrated minority interests to push negative externalities onto the majority (Buchanan and Tullock Reference Buchanan and Tullock1965; Riker and Brams Reference Riker and Brams1973). If we recall the vigorous debate in Parliament as to whether local knowledge would improve the quality of committee decisions, it is conceivable that logrolling might allow local MPs to ensure that the best projects were approved for their constituency. However, knowing that historians have tended to disparage both the number of bills approved and the resulting network, it seems more probable that logrolling facilitated local or even personal interests while foisting the externality of a poor-quality company or an ill-designed network onto the general public.
In this section, we offer a partial test of the hypothesis that logrolling ushered into existence companies of lower social value by looking at their financial performance. Specifically, we test for a difference in the stock prices of the railway companies that were “logrollable” and their peers that were not. As we do not have direct evidence on which companies were actually approved through vote trading, we default to a binary measure, sorting the companies that were passed in the parliamentary sessions of 1845 and 1846 into two groups: those that could have been logrolled due to their connections to MPs and those that could not.Footnote 53
For instance, the Wakefield, Pontefract, and Goole extension railroad project favored the district of Viscount Pollington, who represented Pontefract. In 1846, Pollington sat on committee 16, which was charged with evaluating the Reading, Guildford, and Reigate railway project. This project had been the object of speculation by several MPs, including Ross Donnelly Mangles, who, in addition to representing Guildford, had several thousand pounds tied up in the railway. Mangles happened to sit on committee 36, which oversaw the Wakefield project. Both the Wakefield, Pontefract, and Goole extension and the Reading, Guildford, and Reigate projects were approved by their respective committees. While we cannot be certain that they were approved because of the clear opportunity for Mangles and Pollington to collude, for the purposes of this section, we will consider both railways as “treated”: these are railways whose passage could be the product of collusion. In contrast, we take projects such as the Farnham and Alton branches of the London and South Western railway company, evaluated in committee 16, or the East Riding branches of the York and North Midland railway, considered in committee 36, as untreated, because they were not included in any logrolling cycle.Footnote 54
The year 1847 coincided with a massive crash in equity prices of railways, and many of the firms did not survive, ending up insolvent or absorbed by other railways. Therefore, we expect that acquiring a listing in the stock exchange was a self-selected mechanism, only available to the best-run and most promising companies.Footnote 55 Because the selection into listing might be correlated with our classification of companies according to logrolls, we need to test first for balance between the treatment (companies with logrolling opportunities) and control groups (companies without). To this effect, we collected a number of contemporary markers about the performance (including stock market listing) of all the companies approved in the sessions of 1845 and 1846.Footnote 56 Table 5 lists balance tests for six variables between the two groups of companies, with the information pooled or split by the two parliamentary sessions.
The first variable is the proportion of companies in the two groups (logroll and non-logroll) that were listed in English exchanges.Footnote 57 Even though the percentage of non-logrolled companies that listed was higher (especially in 1846), the difference is not significant. Equally insignificant is the difference in the average number of MPs investing in the two groups of companies. This is consistent with all other evidence that the mechanism for company approval was not simply political patronage (in the form of investments by politicians) but strategic vote trading in the House of Commons. The third variable measures the percentage rate of the intended routes that were open for service by March 1848 by the companies approved in the two sessions. Understandably, completion rates were higher for companies given the go-ahead in 1845, and there appears to be moderate negative selection by logrolled companies, which, however, is not significant.Footnote 58
The next two variables are measures of inputs rather than outputs. Size is the total capital stock (measured in millions of pounds) that companies were authorized to raise from their subscribers. There is no clear size rank between logrolled and non-logrolled companies: the former were larger in 1845 and the latter in 1846, but the differences are never significant. The variable percent funds raised is the ratio between the funds raised by companies until March 1848 and the total amount they were allowed to raise by their acts. Unlike Size, this variable includes both share sales and borrowing.Footnote 59 There is, again, no significant difference between the average rate of fundraising by the two groups of companies. As expected, the ratio is lower for companies approved in 1846, as the stock market crash inevitably increased the costs of raising capital for railway companies. The Economist commented in September 1847 that it was no surprise “that we now see a general movement on the part of the railway interest to suspend, or at least curtail, their present expenditure.”Footnote 60
The final variable is a summary of the capital structure. Gearing is defined as the ratio between debt and equity actually raised by the companies. Once more, the difference in gearing ratios is not significant across company types. Notice also that the ratios are consistently below the legal maximum of one-third, which suggests that companies preferred raising capital from their shareholders to borrowing.Footnote 61 In all cases, the evidence is consistently against selection on observables for companies that could have been approved through logroll and those that could not. Based on this, we move to our test of the impact of logrolling on the subset of companies that gained listings in stock exchanges.
Table 5 TESTS OF EQUALITY OF MEANS, APPROVED COMPANIES

Notes: the p-values are from two-sided tests of equality of means with different variances. We exclude Irish railway companies. †Defined by railway group. *In million pounds.
Sources: Authors’ calculations. See text for descriptions of the data.
Table 6 SUMMARY STATISTICS: TOBIN’S Q AND COMPANY INFORMATION

Sources: Authors’ calculations. See text for descriptions of the data.
To evaluate firm performance, we collected daily share prices from the Railway Monitor, a railway price list published by the Economist, and aggregated the data up to weekly observations in order to deal with the fact that many firms were only occasionally quoted. The price data was pooled across exchanges, as certain companies were more frequently quoted in Leeds, Liverpool, or Manchester than London (Killick and Thomas Reference Killick and Thomas1970). We use as an observation window the period after the completion of the parliamentary approval process, from the end of the 1846 parliamentary session (28 August) until the end of 1847.
We define as dependent variable the Tobin’s-Q for each firm-week pair (Tobin Reference Tobin1969). In order to compute a correct Tobin’s-Q, it was necessary to convert partially paid shares into equivalent fully-paid shares, using the correction derived by Campbell (Reference Campbell2013).Footnote 62 Table 6 contains the summary statistics of the dependent variable and a number of standard controls for the liquidity and volatility of stocks, as well as for the number of MP investors in each listed company.Footnote 63
To test for a conditional effect of logrolls on firms’ market valuation, we regress the log Tobin’s Q on the dummy for logrolls and the other variables listed in Table 6. We include time-fixed effects in all specifications to control for market-wide trends. Since the logrolling variable is time-unvarying, we cannot estimate standard fixed-effects models. Table 7 lists three main specifications: pooled regressions, a random-effects model, and a hybrid model that allows estimating fixed-effects models with time-invariant covariates, such as the logroll dummy or the MP count. This method also provides separate estimates for the between and within effects of time-varying covariates (Allison Reference Allison2009).
Table 7 MODELS OF FIRMS’ STOCK MARKET PERFORMANCE

Notes: The dependent variable is the log Tobin’s Q in Columns (l)-(4) and the log market price in Column (5). Robust standard errors in parentheses, ***p < 0.01,**p < 0.05,*p < 0.1.
Source: See text for definition of variables.
The unconditional estimate of the logroll effect (Column (1)) is negative but insignificant. Adding covariates to the pooled regression increases the size of the coefficient, which becomes significant in the pooled specification (Column (2)). The impact of a logroll is not statistically distinguishable from zero in the random-effects specification (Column (3)). However, the RE model assumes that the between and within effects of the covari-ates are equal, and we can reject this hypothesis from the estimates of the coefficients in the hybrid model (Column (4)). Baltagi (Reference Baltagi2013) shows that this test is equivalent to the Hausman test of the consistency of the random effects estimator, and therefore it implies that the RE are correlated with unobservables. Consequently, our preferred results come from the hybrid model (Column (4)), where the logroll marker is significant, negative, and has a larger size than the previous estimators. If we compare the size of the estimate to the summary statistics in Table 6, we can see that companies that may have owed their existence to logrolling suffered a penalty of approximately half of the mean of the dependent variable. This is a significant quantity, especially in a period of high volatility in stock prices, as in 1846 and 1847. For comparison, we re-estimate the model using actual stock prices instead of fully-paid equivalent prices on the left-hand side. The fit of the model in Column (5) is not as good, but the logroll coefficient is significant and large, implying a 31 percent discount to the stock of companies connected through logrolling opportunities.Footnote 64
The covariates behave as expected. Stocks with higher liquidity (with more frequent prices marked in the list) had higher prices. Stocks with more volatile prices (measured by the monthly standard deviation of prices) have lower prices. We also control for the number of MP investors in each company but actually find a negative relation with stock prices in the pooled model, which is the only specification in which the effect size is significant. It appears that simple MP involvement had little impact on equity prices.
Despite the lack of evidence of selection on observables in Table 5, there are still a number of ways in which this test of company quality may be understating the true effect. If the worst logrolled firms were more likely to fail and were thus less likely to generate observable price data, this would result in us underestimating the size of the performance penalty associated with a logrolled firm. Likewise, the way we encoded treatment bias the results against finding an effect since not all firms that could have been approved by logrolling necessarily were.
In any case, the results are consistent with a pessimistic view of logrolling in this period, in that politicians’ pursuit of local or private interests generated negative externalities for the wider public. We can use simple back-of-the-envelope computations to benchmark the aggregate capital loss to investors. This computation involves three steps.
We start by assuming that 25 percent of the 393 railway projects that received a bill in 1845/46 were approved through logrolls.Footnote 65 The next step is to decide what constituted private investment in railways. The average size of the capital authorized per railway act was £0.4 million. However, as previously mentioned, subscribers to railway scrip were only required to pay a 10 percent deposit prior to the approval by Parliament of the project. Even after approval, companies did not call immediately the remaining 90 percent from the shareholders. The figures in Table 5 imply that companies raised less than 60 percent of their authorized funds up to three years after they received a bill. This figure is not useful, however, because it includes debt and also because it is reported by railway group, rather than by each new line approved in 1845/46. But if we focus on the 85 lines that were approved as self-standing companies (unconnected to an existing group) and exclude debt, the corresponding figure is 44 percent.Footnote 66 We will use this percentage as a benchmark for short-term monetary losses, but there is also a case for using the total authorized capital as the proper basis of evaluation. Even if not all capital was immediately called up, most companies that remained in business after the 1847 crisis raised their full authorized capital within five years (Campbell Reference Campbell2013). Furthermore, Campbell and Turner (Reference Campbell and Turner2010) show that the capital losses from the 1847 crisis were not reversed well into the 1850s.Footnote 67 Faced with ongoing negative capital gains, shareholders were still liable for the full amount of the remaining capital calls, which are reflected in the fully-paid equivalent share prices used in the regressions of Table 7. In other words, the full authorized capital is the proper basis to evaluate the medium-term financial losses for investors.
The third, and final step, involves determining the scale of capital losses. As just explained, because the dependent variable in Model (4) in Table 7 is based on fully-paid equivalent share prices, we should use its point estimate of the logrolling effect, -16 percent, to benchmark the scale of medium-term financial losses.Footnote 68 If, on the other hand, we are interested in quantifying the immediate monetary losses to investors from the drop in value in their partly-paid shares, we should use the point estimate of Model (5), where the left-hand side variable uses the market prices of shares (rather than their fully-paid equivalents). In this case, the price effect of logrolling is estimated to be a 31 percent price drop.
A final caveat comes from the fact that since only about one-fifth of approved companies applied for listing in the London Stock Exchange (Table 5), we miss price information on the remaining 80 percent. As mentioned previously, if acquiring a listing was a marker of quality, we expect that the scale of losses for unlisted companies was no smaller than for listed companies. We assume here, conservatively, that the stock of unlisted companies was discounted by the same proportion of the shares of listed companies.
We collect all these figures in Table 8, where we multiply them to reach a benchmark for the total losses for private investors in railway stock. We report the total amount both in money terms and as a fraction of contemporary GDP.Footnote 69
Table 8 BENCHMARK ESTIMATES OF AGGREGATE FINANCIAL LOSSES

Sources: Authors’ calculations based on assumed scenarios. The source of the numbers is given in the text.
The first line of Table 8 reports the medium-term loss scenario, which adds up to a little over 1 percent of nominal GDP. In the second line, we use the information on effective capital calls and share prices to benchmark the scale of immediate capital losses associated with logrolled companies, which stand at a fraction below the medium-term result. This is not surprising considering that the market price of partly-paid shares reacted to the option value embedded in the unpaid calls (Campbell Reference Campbell2013). In the two final rows, we consider a scenario distinguishing between listed and unlisted companies. In this, we make the extreme assumption that unlisted companies did not raise capital beyond the initial 10 percent deposit required to apply for a bill.Footnote 70 We apply this factor to the 80 percent of lines approved in 1845/46 that were not listed. Adding the result to the losses imputed to the 20 percent listed companies, we still reach a total loss equivalent to one-third of 1 percent of GDP. This is a non-trivial externality from political rent-seeking in and of itself. It appears even more significant when compared with recent estimates of the economic impact of railways in England and Wales. Social savings estimates for 1865 stand at 4.1 percent for the gains from freight traffic (Hawke Reference Hawke1970) and 5 percent for passenger traffic (Leunig Reference Leunig2006). The range of estimates for later periods, however, is very wide and dependent on a number of assumptions about alternative transportation methods, the elasticity of transportation demand, and productivity spillovers to no-transportation sectors (Leunig Reference Leunig2010).
However, there are several reasons why it is not possible to compare directly the return on private investment in railway shares with these estimates of economy-wide social savings. To begin with, the time horizon of social savings estimates is longer than the maximum of five years considered in our benchmarks. Second, unlike social savings, we do not account for the opportunity cost of capital invested in railway projects. Third, investors’ losses are not necessarily a loss to society but wealth transfers from unfortunate shareholders to company promoters, contractors, landholders, and other parties benefiting from the investment in railways. More broadly, the social costs of logrolling will not be fully reflected in the pricing of the companies’ equity over a short period. Recent work has emphasized the importance of initial endowments in pushing economies into better and worse equilibria through path-dependence (Bleakley and Lin Reference Bleakley and Lin2012). The total costs of rent-seeking behavior by parliamentarians could well involve a further impact through the inefficiency of the network that got built (Casson Reference Casson2009). Quantifying the long-term consequences of political rent-seeking, carried through path dependence, is a project in need of further exploration.
CONCLUSION
The mid-1840s saw the promotion of a large fraction of what became the British transport network and the proliferation of numerous railway lines. Parliament’s role in the creation of this network has remained puzzling, as MPs appeared inexplicably lenient in their granting of railway acts, despite occasional vocal opposition by landowners and canal companies. The conjecture that this leniency could have been explained by rent-seeking behavior by MPs is difficult to test because if there were collusion to pass railway bills, it would be tacit and not directly observable. Ironically, a set of institutional reforms precisely intended to thwart outside pressure offer opportunities for testing for the presence of logrolling. This historical context thus offers an opportunity to better understand strategic voting and to explain an enduring historical puzzle. Our findings indicate that logrolling was prevalent and significant, that it accounted for a large fraction of the railways approved by Parliament, in the region of 16 percent to one-third depending on the parliamentary session. If anything, these results are a lower bound on the true prevalence of logrolling due to unobservable trades.
Our analysis verifies not only that logrolling was prevalent, but that in this instance, it had associated costs—decreasing the quality of the approved pool of companies. The short-run costs were born by investors in these companies, who suffered a large capital loss, possibly in the order of 1 percent of GDP. The question of whether logrolling also contributed to degrading the efficiency of the railway network that emerged as a result of Parliament’s deliberations is not answered here. However, the scale of our findings gestures towards what we believe to be a fruitful path forward by exploring the long-term ramifications of collusive political behavior.
Our methodology can be replicated in other settings. As long as the set of feasible trades between politicians is restricted by an exogenous process, peer-effects models can be employed to test for logrolling in political assemblies. An advantage of this approach is that it yields a natural set-up for considering vote trading among any given number of politicians and across a potentially large number of bills. The articulation of logrolling in social network terms offers a flexible framework for thinking about complex strategic arrangements.















