Research Article
Rendezvous Search with Revealed Information: Applications to the Line
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1-15
-
- Article
-
- You have access
- Export citation
Research Papers
A Weakest Link Marked Stopping Problem
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 843-851
-
- Article
-
- You have access
- Export citation
Research Article
Stochastic Epidemic Models in Structured Populations Featuring Dynamic Vaccination and Isolation
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 571-585
-
- Article
-
- You have access
- Export citation
Heavy Tails of Discounted Aggregate Claims in the Continuous-Time Renewal Model
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 285-294
-
- Article
-
- You have access
- Export citation
Research Papers
Bounds for Owen's Multilinear Extension
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 852-864
-
- Article
-
- You have access
- Export citation
Research Article
Distribution-Invariant Risk Measures, Entropy, and Large Deviations
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 16-40
-
- Article
-
- You have access
- Export citation
A Stochastic Maximin Fixed-Point Equation Related to Game Tree Evaluation
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 586-606
-
- Article
-
- You have access
- Export citation
Convolution Equivalence and Infinite Divisibility: Corrections and Corollaries
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 295-305
-
- Article
-
- You have access
- Export citation
Tail Asymptotics for Monotone-Separable Networks
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 306-320
-
- Article
-
- You have access
- Export citation
Characterizations of Conditional Comonotonicity
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 607-617
-
- Article
-
- You have access
- Export citation
Coupling of Two SIR Epidemic Models with Variable Susceptibilities and Infectivities
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 41-57
-
- Article
-
- You have access
- Export citation
Research Papers
Robustness of Delta Hedging for Path-Dependent Options in Local Volatility Models
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 865-879
-
- Article
-
- You have access
- Export citation
Research Article
Thou Shalt not Diversify: Why ‘Two Of Every Sort’?
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 58-70
-
- Article
-
- You have access
- Export citation
A Paradox for Admission Control of Multiclass Queueing Network with Differentiated Service
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 321-331
-
- Article
-
- You have access
- Export citation
Research Papers
On Utility-Based Superreplication Prices of Contingent Claims with Unbounded Payoffs
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 880-888
-
- Article
-
- You have access
- Export citation
Research Article
Asymptotic Behavior of a Generalized TCP Congestion Avoidance Algorithm
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 618-635
-
- Article
-
- You have access
- Export citation
A Stochastic Ordering Property for Leaky Bucket Regulated Flows in Packet Networks
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 332-348
-
- Article
-
- You have access
- Export citation
On Generating Functions of Waiting Times and Numbers of Occurrences of Compound Patterns in a Sequence of Multistate Trials
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 71-81
-
- Article
-
- You have access
- Export citation
Research Papers
Precise Large Deviations for Sums of Random Variables with Consistently Varying Tails in Multi-Risk Models
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 889-900
-
- Article
-
- You have access
- Export citation
Research Article
Stability of Processor Sharing Networks with Simultaneous Resource Requirements
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 636-651
-
- Article
-
- You have access
- Export citation

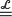 ξ max
ξ max