Research Papers
Nonzero-sum games for continuous-time Markov chains with unbounded discounted payoffs
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 303-320
-
- Article
-
- You have access
- Export citation
Improving on bold play when the gambler is restricted
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 321-333
-
- Article
-
- You have access
- Export citation
Compound Poisson limits for household epidemics
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 334-345
-
- Article
-
- You have access
- Export citation
Heterogeneous population dynamical model: a filtering problem
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 346-361
-
- Article
-
- You have access
- Export citation
Portfolio optimization with unobservable Markov-modulated drift process
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 362-378
-
- Article
-
- You have access
- Export citation
Differentiation of some functionals of risk processes, and optimal reserve allocation
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 379-392
-
- Article
-
- You have access
- Export citation
Rarity and exponentiality: an extension of Keilson's theorem, with applications
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 393-406
-
- Article
-
- You have access
- Export citation
Geometrical characteristics of Gaussian sea waves
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 407-425
-
- Article
-
- You have access
- Export citation
Multiperiod conditional distribution functions for conditionally normal GARCH(1, 1) models
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 426-445
-
- Article
-
- You have access
- Export citation
Multitype branching processes observing particles of a given type
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 446-462
-
- Article
-
- You have access
- Export citation
Asymptotic behaviour of critical controlled branching processes with random control functions
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 463-477
-
- Article
-
- You have access
- Export citation
Processor-sharing and random-service queues with semi-Markovian arrivals
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 478-490
-
- Article
-
- You have access
- Export citation
Fluid limit of generalized Jackson queueing networks with stationary and ergodic arrivals and service times
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 491-512
-
- Article
-
- You have access
- Export citation
Tails in generalized Jackson networks with subexponential service-time distributions
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 513-530
-
- Article
-
- You have access
- Export citation
Efficient algorithms for transient analysis of stochastic fluid flow models
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 531-549
-
- Article
-
- You have access
- Export citation
Burgers' turbulence problem with linear or quadratic external potential
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 550-565
-
- Article
-
- You have access
- Export citation
The lifetime of a random set
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 566-580
-
- Article
-
- You have access
- Export citation
Short Communications
B-stability
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 581-586
-
- Article
-
- You have access
- Export citation
Optimization under the PMλ,τ policy of a finite dam with both continuous and jumpwise inputs
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 587-594
-
- Article
-
- You have access
- Export citation
Front matter
JPR volume 42 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. f1-f2
-
- Article
-
- You have access
- Export citation



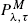 policy, where the input of water is formed by a Wiener process subject to random jumps arriving according to a Poisson process. The long-run average cost per unit time is obtained after assigning costs to the changes of release rate, a reward to each unit of output, and a penalty that is a function of the level of water in the reservoir.
policy, where the input of water is formed by a Wiener process subject to random jumps arriving according to a Poisson process. The long-run average cost per unit time is obtained after assigning costs to the changes of release rate, a reward to each unit of output, and a penalty that is a function of the level of water in the reservoir.