No CrossRef data available.
Article contents
Stochastic ordering results on the duration of the gambler’s ruin game
Published online by Cambridge University Press: 06 October 2023
Abstract
In the classical gambler’s ruin problem, the gambler plays an adversary with initial capitals z and 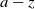 $a-z$, respectively, where
$a-z$, respectively, where 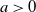 $a>0$ and
$a>0$ and 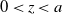 $0< z < a$ are integers. At each round, the gambler wins or loses a dollar with probabilities p and
$0< z < a$ are integers. At each round, the gambler wins or loses a dollar with probabilities p and 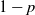 $1-p$. The game continues until one of the two players is ruined. For even a and
$1-p$. The game continues until one of the two players is ruined. For even a and 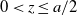 $0<z\leq {a}/{2}$, the family of distributions of the duration (total number of rounds) of the game indexed by
$0<z\leq {a}/{2}$, the family of distributions of the duration (total number of rounds) of the game indexed by 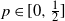 $p \in [0,{\frac{1}{2}}]$ is shown to have monotone (increasing) likelihood ratio, while for
$p \in [0,{\frac{1}{2}}]$ is shown to have monotone (increasing) likelihood ratio, while for  ${a}/{2} \leq z<a$, the family of distributions of the duration indexed by
${a}/{2} \leq z<a$, the family of distributions of the duration indexed by 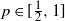 $p \in [{\frac{1}{2}}, 1]$ has monotone (decreasing) likelihood ratio. In particular, for
$p \in [{\frac{1}{2}}, 1]$ has monotone (decreasing) likelihood ratio. In particular, for 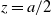 $z={a}/{2}$, in terms of the likelihood ratio order, the distribution of the duration is maximized over
$z={a}/{2}$, in terms of the likelihood ratio order, the distribution of the duration is maximized over 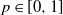 $p \in [0,1]$ by
$p \in [0,1]$ by 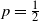 $p={\frac{1}{2}}$. The case of odd a is also considered in terms of the usual stochastic order. Furthermore, as a limit, the first exit time of Brownian motion is briefly discussed.
$p={\frac{1}{2}}$. The case of odd a is also considered in terms of the usual stochastic order. Furthermore, as a limit, the first exit time of Brownian motion is briefly discussed.
Keywords
MSC classification
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust





