Hostname: page-component-76fb5796d-r6qrq Total loading time: 0 Render date: 2024-04-28T05:31:30.088Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability and characterisation conditions in negative programming

Published online by Cambridge University Press:  14 July 2016

P. Whittle
P. Whittle*
Affiliation:
University of Cambridge
*
∗Postal address: Statistical Laboratory, 16 Mill Lane, Cambridge CB2 1SB, U.K.
Get access Rights & Permissions [Opens in a new window]

Abstract

Let F be the infinite-horizon minimal cost function, and FKS the minimal cost function for horizon s and terminal cost function K. In Section 2 we define the ‘stable domain' (the set of K for which 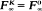), determine some of its properties, and relate these to the questions of stability of the process (whether 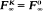) and whether a given solution of the dynamic programming equation can be identified with F These ideas are developed in Sections 3 and 5 for various strengthenings and weakenings of the hypothesis of non-negative costs. In Section 5 we derive a new sufficient condition for stability and for characterisation of F.

Keywords

DYNAMIC PROGRAMMINGNEGATIVE PROGRAMMING
Type
Research Papers
Information
Journal of Applied Probability , Volume 17 , Issue 3 , September 1980 , pp. 635 - 645
Copyright
Copyright © Applied Probability Trust 1980 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bertsekas, D. P. (1976) Dynamic Programming and Stochastic Control. Academic Press, New York.Google Scholar
Hinderer, K. (1970) Foundations of Non-Stationary Dynamic Programming with Discrete Time Parameter. Springer-Verlag, Berlin.CrossRefGoogle Scholar
Whittle, P. (1979) A simple condition for regularity in negative programming. J. Appl. Prob. 16, 305–318.Google Scholar