Research Article
QUIVERS, LONG EXACT SEQUENCES AND HORN TYPE INEQUALITIES II
-
- Published online by Cambridge University Press:
- 01 May 2009, pp. 201-217
-
- Article
-
- You have access
- Export citation
CONSTANT SCALAR CURVATURE HYPERSURFACES WITH SECOND-ORDER UMBILICITY
-
- Published online by Cambridge University Press:
- 01 May 2009, pp. 219-241
-
- Article
-
- You have access
- Export citation
ON INTEGER SEQUENCES GENERATED BY LINEAR MAPS
-
- Published online by Cambridge University Press:
- 01 May 2009, pp. 243-252
-
- Article
-
- You have access
- Export citation
GK–DIMENSION OF ALGEBRAS WITH MANY GENERIC RELATIONS*
-
- Published online by Cambridge University Press:
- 01 May 2009, pp. 253-256
-
- Article
-
- You have access
- Export citation
COMPACT TOEPLITZ OPERATORS WITH CONTINUOUS SYMBOLS
-
- Published online by Cambridge University Press:
- 01 May 2009, pp. 257-261
-
- Article
-
- You have access
- Export citation
THE GROUP OF AUTOMORPHISMS OF THE FIRST WEYL ALGEBRA IN PRIME CHARACTERISTIC AND THE RESTRICTION MAP
-
- Published online by Cambridge University Press:
- 01 May 2009, pp. 263-274
-
- Article
-
- You have access
- Export citation
ON AN INTEGRAL OPERATOR FROM THE ZYGMUND SPACE TO THE BLOCH-TYPE SPACE ON THE UNIT BALL
-
- Published online by Cambridge University Press:
- 01 May 2009, pp. 275-287
-
- Article
-
- You have access
- Export citation
GENERALISED FERMAT HYPERMAPS AND GALOIS ORBITS
-
- Published online by Cambridge University Press:
- 01 May 2009, pp. 289-299
-
- Article
-
- You have access
- Export citation
PTOLEMAIC SPACES AND CAT(0)
-
- Published online by Cambridge University Press:
- 01 May 2009, pp. 301-314
-
- Article
-
- You have access
- Export citation
A CHARACTERISATION OF BERGMAN SPACES ON THE UNIT BALL OF ℂn
-
- Published online by Cambridge University Press:
- 01 May 2009, pp. 315-330
-
- Article
-
- You have access
- Export citation
PINCHING THEOREMS FOR TOTALLY REAL MINIMAL SUBMANIFOLDS IN CPn
-
- Published online by Cambridge University Press:
- 01 May 2009, pp. 331-339
-
- Article
-
- You have access
- Export citation
GROUPS IN WHICH NORMAL CLOSURES OF ELEMENTS HAVE BOUNDEDLY FINITE RANK
-
- Published online by Cambridge University Press:
- 01 May 2009, pp. 341-345
-
- Article
-
- You have access
- Export citation
MODULES WITH FI-EXTENDING HULLS
-
- Published online by Cambridge University Press:
- 01 May 2009, pp. 347-357
-
- Article
-
- You have access
- Export citation
ON MINIMAL SUBGROUPS OF FINITE GROUPS
-
- Published online by Cambridge University Press:
- 01 May 2009, pp. 359-366
-
- Article
-
- You have access
- Export citation
EXISTENCE OF POSITIVE SOLUTION FOR A QUASI-LINEAR PROBLEM WITH CRITICAL GROWTH IN
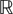 N+
N+
-
- Published online by Cambridge University Press:
- 01 May 2009, pp. 367-383
-
- Article
-
- You have access
- Export citation
A CHARACTERIZATION OF SELF-ADJOINT OPERATORS DETERMINED BY THE WEAK FORMULATION OF SECOND-ORDER SINGULAR DIFFERENTIAL EXPRESSIONS
-
- Published online by Cambridge University Press:
- 01 May 2009, pp. 385-404
-
- Article
-
- You have access
- Export citation
RADICAL FORMULA AND WEAKLY PRIME SUBMODULES
-
- Published online by Cambridge University Press:
- 01 May 2009, pp. 405-412
-
- Article
-
- You have access
- Export citation
SCALAR CURVATURE OF HYPERSURFACES WITH CONSTANT MEAN CURVATURE IN A SPHERE
-
- Published online by Cambridge University Press:
- 01 May 2009, pp. 413-423
-
- Article
-
- You have access
- Export citation
Front Cover (OFC, IFC) and matter
GMJ volume 51 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 01 May 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
GMJ volume 51 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 01 May 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

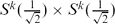 embedded in the Euclidean sphere
embedded in the Euclidean sphere  whose support contains the unit sphere
whose support contains the unit sphere  , let
, let 
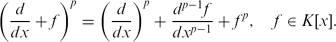
 . The boundedness and compactness of the operator from the Zygmund space to the Bloch-type space
. The boundedness and compactness of the operator from the Zygmund space to the Bloch-type space 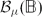 or the little Bloch-type space
or the little Bloch-type space 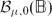 are investigated.
are investigated.
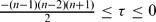 , then
, then 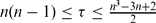 , then
, then 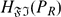 (called the absolute FI-extending hull of
(called the absolute FI-extending hull of 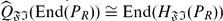 , where
, where  is the smallest right FI-extending right ring of quotients of End(
is the smallest right FI-extending right ring of quotients of End(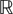
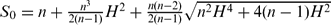 .
.