Article contents
EXISTENCE OF POSITIVE SOLUTION FOR A QUASI-LINEAR PROBLEM WITH CRITICAL GROWTH IN 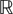
Published online by Cambridge University Press: 01 May 2009
Abstract
In this paper we show existence of positive solutions for a class of quasi-linear problems with Neumann boundary conditions defined in a half-space and involving the critical exponent.
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 2009
References
REFERENCES
- 3
- Cited by


