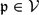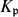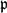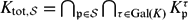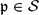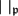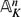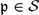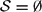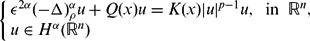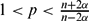Research Article
ON THE CONJUGACY PROBLEM IN CERTAIN METABELIAN GROUPS
-
- Published online by Cambridge University Press:
- 20 June 2018, pp. 251-269
-
- Article
-
- You have access
- Export citation
FREQUENTLY HYPERCYCLIC BILATERAL SHIFTS
- Part of:
-
- Published online by Cambridge University Press:
- 20 June 2018, pp. 271-286
-
- Article
-
- You have access
- Export citation
EXOTIC FINITE FUNCTORIAL SEMI-NORMS ON SINGULAR HOMOLOGY
- Part of:
-
- Published online by Cambridge University Press:
- 20 June 2018, pp. 287-295
-
- Article
-
- You have access
- Export citation
HIGGS BUNDLES OVER ELLIPTIC CURVES FOR COMPLEX REDUCTIVE GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 16 July 2018, pp. 297-320
-
- Article
-
- You have access
- Export citation
ENDOMORPHISMS OF EXOTIC MODELS
-
- Published online by Cambridge University Press:
- 20 June 2018, pp. 321-348
-
- Article
-
- You have access
- Export citation
HOMOTOPY TYPES OF GAUGE GROUPS OVER NON-SIMPLYCONNECTED CLOSED 4-MANIFOLDS
- Part of:
-
- Published online by Cambridge University Press:
- 20 June 2018, pp. 349-371
-
- Article
-
- You have access
- Export citation
STRONG APPROXIMATION THEOREM FOR ABSOLUTELY IRREDUCIBLE VARIETIES OVER THE COMPOSITUM OF ALL SYMMETRIC EXTENSIONS OF A GLOBAL FIELD
- Part of:
-
- Published online by Cambridge University Press:
- 13 July 2018, pp. 373-380
-
- Article
-
- You have access
- Export citation
A STRUCTURED DESCRIPTION OF THE GENUS SPECTRUM OF ABELIAN p-GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 10 July 2018, pp. 381-423
-
- Article
-
- You have access
- Export citation
FOCAL SURFACES OF WAVE FRONTS IN THE EUCLIDEAN 3-SPACE
- Part of:
-
- Published online by Cambridge University Press:
- 13 July 2018, pp. 425-440
-
- Article
-
- You have access
- Export citation
EXISTENCE AND CONCENTRATION OF SOLUTION FOR A NON-LOCAL REGIONAL SCHRÖDINGER EQUATION WITH COMPETING POTENTIALS
-
- Published online by Cambridge University Press:
- 25 July 2018, pp. 441-460
-
- Article
-
- You have access
- Export citation
BONGARTZ τ-COMPLEMENTS OVER SPLIT-BY-NILPOTENT EXTENSIONS
-
- Published online by Cambridge University Press:
- 30 July 2018, pp. 461-470
-
- Article
-
- You have access
- Export citation
A PERTURBATION AND GENERIC SMOOTHNESS OF THE VAFA–WITTEN MODULI SPACES ON CLOSED SYMPLECTIC FOUR-MANIFOLDS
-
- Published online by Cambridge University Press:
- 13 July 2018, pp. 471-486
-
- Article
-
- You have access
- Export citation
EXTREME POINTS FOR COMBINATORIAL BANACH SPACES
-
- Published online by Cambridge University Press:
- 27 July 2018, pp. 487-500
-
- Article
-
- You have access
- Export citation
Front Cover (OFC, IFC) and matter
GMJ volume 61 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 26 March 2019, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
GMJ volume 61 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 26 March 2019, pp. b1-b3
-
- Article
-
- You have access
- Export citation