Hostname: page-component-848d4c4894-2pzkn Total loading time: 0 Render date: 2024-04-30T11:57:02.550Z Has data issue: false hasContentIssue false
  • English
  • Français

On the monodromy groups of lifted Euler equations

Published online by Cambridge University Press:  18 May 2009

Kathryn Kuiken  and
John T. Masterson
Kathryn Kuiken
Affiliation:
Polytechnic Institute Of New York, 333 Jay Street, Brooklyn, New York 11201, U.S.A.
John T. Masterson
Affiliation:
Seton Hall University, 435 South Orange Avenue, South Orange, New Jersey 07079, U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [13], Poincaré asked the following question: Which abstract groups can appear as monodromy groups [14] of second order, linear, homogeneous differential equations with meromorphic coefficients (which might depend on one or more parameters) on ℂ? In the present paper, we initiate a classification of monodromy groups of differential equations on compact Riemann surfaces of genus 1. We proceed as follows: Let

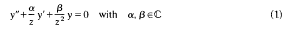
be the general Euler equation [1] which has two regular singular points at 0 and λ in the extended complex plane C. Further, let yu(z)(v – 1,2) be an arbitrary but fixed pair of linearly independent solutions to (1) valid in a neighborhood of some ordinary point. Analytic continuation of each solution along a closed loop A in C–{0, λ}, starting and ending at some fixed base point, produces a new solution yv,A (v = 1, 2) which can be expressed as

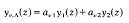
where the constants avlx (v1 ν = l,2) in C depend on the homotopy class [A] of A. Clearly, y1,A(z)/y2,A(z) = To(y1(z)/y2(z)) where the Möbius transformation T:w→ (a11W + a12)/(a21W + a22) depends on [A]. The set of all Mobius transformations T belonging to every possible closed loop A in C–{0,λ} forms a group G, called the monodromy group of the Euler equation (1). G is generated by the Mobius transformation belonging to a simple, closed loop Ao encircling 0. Hence, G is cyclic.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 25 , Issue 1 , January 1984 , pp. 47 - 57
Copyright
Copyright © Glasgow Mathematical Journal Trust 1984

References

REFERENCES

1.Boyce, W. E. and DiPrima, R. C., Elementary differential equations and boundary value problems (Wiley 1977).Google Scholar
2.Erdélyi, A. et al. , Higher transcendental functions Bateman Manuscript Project, Vol. 1 (McGraw-Hill, 1953).Google Scholar
3.Farkas, H. and Kra, I., Riemann surfaces(Springer-Verlag, 1980).CrossRefGoogle Scholar
4.Gunning, R. C., Special coordinate coverings of Riemann surfaces, Math. Annalen, 170, (1967) 67–86.Google Scholar
5.Hall, M., The theory of groups (MacMillan 1970).Google Scholar
6.Hochstadt, H., The functions of mathematical physics (Interscience, 1971).Google Scholar
7.Kuiken, K., The effect of rational substitutions on the monodromy group of the general nth order equation of the Fuchsian class, Math. Z, 163, (1978) 111–119.CrossRefGoogle Scholar
8.Lehner, J., A short course in automorphic functions (Holt, Rinehart and Winston, 1966).Google Scholar
9.Magnus, W., Karrass, A. and Solitar, D., Combinatorial group theory (Interscience, 1966).Google Scholar
10.Massey, W. S., Algebraic topology: an introduction (Harcourt, Brace and World, New York, 1967).Google Scholar
11.Masterson, J. T., Branched affine (or projective) structures on Riemann surfaces, Ph.D. Thesis, (1981) Polytechnic Institute of New York, (to appear).Google Scholar
12.Nevanlinna, R. and Paatero, V., Introduction to complex analysis (Addison-Wesley, 1962).Google Scholar
13.Poincaré, H., Sur les groupes des équations linéaires, Acta Math., 4, (1884) 201–312.CrossRefGoogle Scholar
14.Poole, E. G. C., Theory of linear differential equations(Dover, 1960).Google Scholar