Hostname: page-component-76fb5796d-r6qrq Total loading time: 0 Render date: 2024-04-27T01:19:35.924Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE LINEAR COMBINANTS OF A BINARY PENCIL

Published online by Cambridge University Press:  01 September 2009

ABDELMALEK ABDESSELAM  and
JAYDEEP CHIPALKATTI
ABDELMALEK ABDESSELAM
Affiliation:
Kerchof Hall Department of Mathematics, University of Virginia, PO Box 400137, Charlottesville, VA 22904-4137, USA e-mail: malek@virginia.edu
JAYDEEP CHIPALKATTI
Affiliation:
Machray Hall, Department of Mathematics, University of Manitoba, Winnipeg MB R3T 2N2, Canada e-mail: chipalka@cc.umanitoba.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let A, B denote binary forms of order d, and let 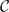2r−1 = (A, B)2r−1 be the sequence of their linear combinants for 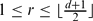. It is known that 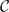1, 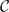3 together determine the pencil {A + λ B}λ∈P1 and hence indirectly the higher combinants 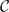2r−1. In this paper we exhibit explicit formulae for all r ≥ 3, which allow us to recover 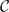2r−1 from the knowledge of 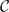1 and 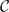3. The calculations make use of the symbolic method in classical invariant theory, as well as the quantum theory of angular momentum. Our theorem pertains to the plethysm representation ∧2Sd for the group SL2. We give an example for the group SL3 to show that such a result may hold for other categories of representations.

Keywords

13A5022E70
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 51 , Issue 3 , September 2009 , pp. 481 - 498
Copyright
Copyright © Glasgow Mathematical Journal Trust 2009

References

REFERENCES

1.Abdesselam, A. and Chipalkatti, J., The bipartite Brill–Gordan locus and angular momentum, Transform. Grp. 11 (3) (2006), 341–370.CrossRefGoogle Scholar
2.Abdesselam, A. and Chipalkatti, J., On the Wronskian combinants of binary forms, J. Pure Appl. Algebra 210 (1) (2007), 43–61.CrossRefGoogle Scholar
3.Abdesselam, A. and Chipalkatti, J., The higher transvectants are redundant. Preprint arXiv:0801.1533v1 [math.AG] (2008).Google Scholar
4.Carré, C. and Leclerc, B., Splitting the square of a Schur function into its symmetric and antisymmetric parts, J. Algebraic Combin. 4 (3) (1995), 201–231.CrossRefGoogle Scholar
5.Chipalkatti, J., On the invariant theory of the Bézoutiant, Beiträge Algebra Geom. 47 (2) (2006), 397–417.Google Scholar
6.Clebsch, A., Theorie der Binaren Algebraischen Formen (Teubner, Leipzig, Germany, 1872).Google Scholar
7.Dolgachev, I., Lectures on invariant theory, London Mathematical Society Lecture Notes No. 296 (Cambridge University Press, Cambridge, 2003).CrossRefGoogle Scholar
8.Fulton, W. and Harris, J., Representation theory: A first course, Graduate Texts in Mathematics. (Springer, New York, 1991).Google Scholar
9.Glenn, O., The theory of invariants (Ginn and Co., Boston, 1915).Google Scholar
10.Gordan, P., Ueber Combinanten, Math. Ann. 5 (1872), 95–122.CrossRefGoogle Scholar
11.Grace, J. H. and Young, A., The algebra of invariants (Chelsea, New York, 1962).Google Scholar
12.Meulien, M., Sur les invariants des pinceaux de formes quintiques binaires, Ann. Inst. Fourier (Grenoble) 54 (2004), 21–51.CrossRefGoogle Scholar
13.Newstead, P. E., Covariants of pencils of binary cubics, Proc. R. Soc. Edinburgh Sect. A, 91 (3-4) (1981–1982), 181–183.CrossRefGoogle Scholar
14.Olver, P., Classical invariant theory, London Mathematical Society Student Texts (Cambridge University Press, Cambridge, 1999).CrossRefGoogle Scholar
15.Shenton, W., Linear combinants of systems of binary forms, with the syzygies of the second degree connecting them, Am. J. Math. 37 (3) (1915), 247–271.CrossRefGoogle Scholar
16.Shepherd-Barron, N. I., The rationality of some moduli spaces of plane curves, Compositio Math. 67 (1988), 51–88.Google Scholar
17.Sturmfels, B., Algorithms in invariant theory, Texts and Monographs in Symbolic Computation (Springer, Vienna, 1993).CrossRefGoogle Scholar
18.Wall, C. T. C., Pencils of binary quartics, Rend. Sem. Mat. Univ. Padova 99 (1998), 197–217.Google Scholar