Hostname: page-component-76fb5796d-45l2p Total loading time: 0 Render date: 2024-04-27T02:32:43.795Z Has data issue: false hasContentIssue false
  • English
  • Français

On right duo p.p. rings

Published online by Cambridge University Press:  18 May 2009

A. W. Chatters  and
Weimin Xue
A. W. Chatters
Affiliation:
School of MathematicsUniversity WalkBristol BS8 1TW
Weimin Xue
Affiliation:
Department of MathematicsUniversity of Maine Orono, Maine 04469, U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Throughout the paper, rings are associative rings with identity. A ring is called right duo if every right ideal is two-sided, and it is called right p.p. if every principal right ideal is projective. A left duo (p.p.) ring is denned similarly, and a duo (p.p.) ring will mean a ring which is both right and left duo (p.p.). There is a right p.p. ring that is not left p.p. (see Chase [2[). Small [9] proved that right p.p. implies left p.p. if there are no infinite sets of orthogonal idempotents, and Endo [5, Proposition 2] has shown the same implication in the case where each idempotent in the ring is central. Since Courter [3, Theorem 1.3] noted that every idempotent in a right duo ring is central, we can simply speak of right duo p.p. rings. A typical example of a right duo ring which is not left duo is the following. Let F be a field and F(x) the field of rational functions over F. Let R = F(x)× F(x) as an additive group and define the multiplication as follows:

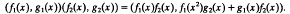
Then R is a local artinian ring with c(RR) = 2 and c(RR)= 3. Thus R is right duo but not left due.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 32 , Issue 2 , May 1990 , pp. 221 - 225
Copyright
Copyright © Glasgow Mathematical Journal Trust 1990

References

REFERENCES

1.Camillo, V. P., A note on semi-hereditary rings, Arch. Math. (Basel) 24 (1973), 142–143.CrossRefGoogle Scholar
2.Chase, S. U., A generalization of the ring of triangular matrices, Nagoya Math. J. 18 (1961), 13–25.CrossRefGoogle Scholar
3.Courter, R. C., Finite dimensional right duo algebras are duo, Proc. Amer. Math. Soc. 84 (1982), 157–161.Google Scholar
4.Dedekind, R., liber die Begriindung der Idealtheorie, Nachr. Ges. Wiss. Göttingen (1895), 106–113.Google Scholar
5.Endo, S., Note on p.p. rings, Nagoya Math. J. 17 (1960), 16–170.CrossRefGoogle Scholar
6.Jensen, C. U., On characterizations of Priifer rings, Math. Scand. 13 (1963), 90–98.CrossRefGoogle Scholar
7.Jϕndrup, S., p.p. rings and finitely generated flat ideals, Proc. Amer. Math. Soc. 28 (1971), 431–435.Google Scholar
8.Rotman, J. J., An Introduction to Homological Algebra (Academic Press, 1979).Google Scholar
9.Small, L. W., Semihereditary rings, Bull. Amer. Math. Soc. 73 (1967), 656–658.CrossRefGoogle Scholar
10.Tuganbaev, A. A., Distributive modules, Russian Math. Surveys 35(5) (1980), 275–276.CrossRefGoogle Scholar
11.Tuganvaev, A. A., Rings with flat right ideals and distributive rings, Math. Notes 38 (1985), 631–636.CrossRefGoogle Scholar
12.Tuganbaev, A. A., Hereditary rings, Math. Notes 41 (1987), 173–177.CrossRefGoogle Scholar
13.Vasconcelos, W. V., On finitely generated fiat modules, Trans. Amer. Math. Soc. 138 (1969), 505–512.CrossRefGoogle Scholar