Hostname: page-component-76fb5796d-22dnz Total loading time: 0 Render date: 2024-04-26T14:29:14.142Z Has data issue: false hasContentIssue false
  • English
  • Français

On normal derivations of Hilbert–Schmidt type

Published online by Cambridge University Press:  18 May 2009

Fuad Kittaneh
Fuad Kittaneh*
Affiliation:
Department of Mathematics, United Arab Emirates University, P.O. Box 15551, Al-Ain, U.A.E.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let H denote a separable, infinite dimensional Hilbert space. Let B(H), C2 and C1 denote the algebra of all bounded linear operators acting on H, the Hilbert–Schmidt class and the trace class in B(H) respectively. It is well known that C2 and C1 each form a two-sided-ideal in B(H) and C2 is itself a Hilbert space with the inner product

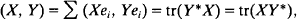
where {ei} is any orthonormal basis of H and tr(.) is the natural trace on C1. The Hilbert–Schmidt norm of X ∈ C2 is given by ⅡXⅡ2=(X, X)½.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 29 , Issue 2 , July 1987 , pp. 245 - 248
Copyright
Copyright © Glasgow Mathematical Journal Trust 1987

References

1. Anderson, J. H., On normal derivations, Proc. Amer. Math. Soc. 38 (1973), 135–140.CrossRefGoogle Scholar
2. Berger, C. A. and Shaw, B. I., Self-commutators of multicyclic hyponormal operators are always trace class, Bull. Amer. Math. Soc. 79 (1973), 1193–1199.CrossRefGoogle Scholar
3. Fuglede, B., A commutativity theorem for normal operators, Proc. Nat. Acad. Sci. U.S.A. 36 (1950), 35–40.CrossRefGoogle ScholarPubMed
4. Kittaneh, Fuad, On generalized Fuglede–Putnam theorems of Hilbert–Schmidt type, Proc. Amer. Math. Soc. 88 (1983), 293–298.CrossRefGoogle Scholar
5. Kittaneh, Fuad, Commutators of Cp type, Thesis, (Indiana University, 1982).Google Scholar
6. Weiss, G., The Fuglede commutativity theorem modulo the Hilbert–Schmidt class and generating functions for matrix operators I. Trans. Amer. Math. Soc. 246 (1978), 193–209.Google Scholar
7. Yoshino, T., Subnormal operators with a cyclic vector, Tohoku Math. J. 21 (1969), 47–55.CrossRefGoogle Scholar