Hostname: page-component-77c89778f8-m42fx Total loading time: 0 Render date: 2024-07-21T04:18:48.790Z Has data issue: false hasContentIssue false
  • English
  • Français

On entire functions with gap power series

Published online by Cambridge University Press:  18 May 2009

J. M. Anderson  and
K. G. Binmore
J. M. Anderson
Affiliation:
University College, London
K. G. Binmore
Affiliation:
London School of Economics
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this note we consider transcendental entire functions

whose power series contain gaps, i.e.

where Λ = {λk} is a suitable set of positive integers. We denote the set of all such functions f(z) by E(Λ). As usual M(r) = M(r, f) denotes the maximummodulus of f(z) on the circle |z| = r. The order p and the lower order λ of f(z) are defined by

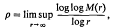
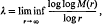
respectively.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 12 , Issue 2 , September 1971 , pp. 89 - 97
Copyright
Copyright © Glasgow Mathematical Journal Trust 1971

References

REFERENCES

1.Anderson, J. M. and Binmore, K. G., Coefficient estimates for lacunary power series and Dirichlet series I, Proc. London Math. Soc. (3) 18 (1968), 36–48.CrossRefGoogle Scholar
2.Edrei, A., Gap and density theorems for entire functions, Scripta Math. 23 (1957), 1–25.Google Scholar
3.Fuchs, W. H. J., On the closure of , Proc. Cambridge Philos. Soc. 42 (1946), 91–105.CrossRefGoogle Scholar
4.Macintyre, A. J., Asymptotic paths of integral functions with gap power series, Proc. London Math. Soc. (3) 2 (1952), 286–296.CrossRefGoogle Scholar
5.Mandelbrojt, S., Séries adhérentes, Régularisation des suites, Applications (Paris 1955).Google Scholar
6.Pólya, G., Untersuchungen über Lücken und Singularitäten von Potenzreihen, Math. Z. 29 (1929), 549–640.CrossRefGoogle Scholar