Article contents
NORM OF THE HILBERT MATRIX OPERATOR ON THE WEIGHTED BERGMAN SPACES
Published online by Cambridge University Press: 18 October 2017
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
We find the lower bound for the norm of the Hilbert matrix operator H on the weighted Bergman space Ap,α
We show that if 4 ≤ 2(α + 2) ≤ p, then ∥H∥Ap,α → Ap,α = 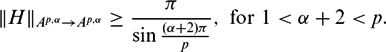 \begin{equation*}
\|H\|_{A^{p,\alpha}\rightarrow A^{p,\alpha}}\geq\frac{\pi}{\sin{\frac{(\alpha+2)\pi}{p}}}, \,\, \textnormal{for} \,\, 1<\alpha+2<p.
\end{equation*}
\begin{equation*}
\|H\|_{A^{p,\alpha}\rightarrow A^{p,\alpha}}\geq\frac{\pi}{\sin{\frac{(\alpha+2)\pi}{p}}}, \,\, \textnormal{for} \,\, 1<\alpha+2<p.
\end{equation*} $\frac{\pi}{\sin{\frac{(\alpha+2)\pi}{p}}}$, while if 2 ≤ α +2 < p < 2(α+2), upper bound for the norm ∥H∥Ap,α → Ap,α, better then known, is obtained.
$\frac{\pi}{\sin{\frac{(\alpha+2)\pi}{p}}}$, while if 2 ≤ α +2 < p < 2(α+2), upper bound for the norm ∥H∥Ap,α → Ap,α, better then known, is obtained.
MSC classification
Secondary:
30H20: Bergman spaces, Fock spaces
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 2017
References
REFERENCES
1. Diamantopoulos, E., Hilbert matrix on Bergman spaces, Illinois J. Math. 48 (3) (2004), 1067–1078.Google Scholar
2. Diamantopoulos, E. and Siskakis, A. G., Composition operators and the Hilbert matrix, Studia Math. 140 (2) (2000), 191–198.Google Scholar
3. Dostanić, M., Jevtić, M. and Vukotić, D., Norm of the Hilbert matrix on Bergman and Hardy spaces and theorem of Nehari type, J. Funct. Anal. 254 (2008), 2800–2815.Google Scholar
4. Duren, P. L. and Schuster, A. P., Bergman spaces, Math. Surveys Monogr., vol. 100 (American Mathematical Society, Providence, RI, 2004).CrossRefGoogle Scholar
5. Gogolin, A. O., Lectures on complex integration, Undergraduate Lecture Notes in Physics (Springer, Cham, Switzerland, 2014).Google Scholar
6. Jevtić, M. and Karapetrović, B., Hilbert matrix operator on Besov spaces, Publ. Math. Debrecen 90/3–4 (2017), 359–371.CrossRefGoogle Scholar
7. Jevtić, M. and Karapetrović, B., Hilbert matrix on spaces of Bergman-type, J. Math. Anal. Appl. 453 (2017), 241–254.Google Scholar
8. Jevtić, M., Vukotić, D. and Arsenović, M., Taylor coefficients and coefficient multipliers of Hardy and Bergman–type spaces, RSME Springer Series 2 (Springer, Cham, Switzerland, 2016).Google Scholar
9. Karapetrović, B., Libera and Hilbert matrix operator on logarithmically weighted Bergman, Bloch and Hardy-Bloch spaces, Czech. Math. J. (accepted for publication).Google Scholar
10. Magnus, W., On the spectrum of Hilbert's matrix, Amer. J. Math. 72 (1950), 699–704.Google Scholar
11. Pavlović, M., Function Classes on the Unit Disc. An Introduction, De Gruyter Stud. Math., vol. 52 (De Gruyter, Berlin, 2014).Google Scholar
- 7
- Cited by




