Hostname: page-component-848d4c4894-hfldf Total loading time: 0 Render date: 2024-06-08T10:45:53.567Z Has data issue: false hasContentIssue false
  • English
  • Français

Continuity and differentiability properties of the Nemitskii operator in Hölder spaces

Published online by Cambridge University Press:  18 May 2009

Rita Nugari
Rita Nugari
Affiliation:
Università dègli Studi della Calabria, Dipartimento di Matematica, 87036 Arcavacata di Rende (Cosenza), Italy
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let ℝn be the n-dimensional Euclidean space with the usual norm denoted by |·| In what follows 蒆 will denote an open bounded subset of ℝn, and 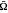its closure.

For α ∊(0,1], 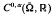is the space of all functions 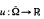such that:

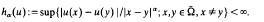
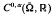is called the Holder space with exponent a and is a Banach space when endowed with the norm:

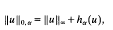
where ‖u‖∞ is, as usual, defined by:

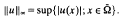
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 30 , Issue 1 , January 1988 , pp. 59 - 65
Copyright
Copyright © Glasgow Mathematical Journal Trust 1988

References

1.Berger, M. S., Nonlinearity and functional analysis, (Academic Press, 1977).Google Scholar
2.Elworthy, K. D. and Tromba, A. J., Degree theory on Banach manifolds, Proc. Symp. Pure Mathematics 18 (AMS, Providence, 1970).Google Scholar
3.Valent, T., A property of multiplication in Sobolev spaces. Some applications, Rend. Sent. Mat. Univ. Padova 74 (1985), 63–73.Google Scholar