Hostname: page-component-848d4c4894-mwx4w Total loading time: 0 Render date: 2024-06-23T08:32:46.541Z Has data issue: false hasContentIssue false
  • English
  • Français

Classification of tensor product immersions which are of 1-type

Published online by Cambridge University Press:  18 May 2009

Bang-Yen Chen
Bang-Yen Chen
Affiliation:
Department of Mathematics, Michigan State University, East Lansing, Michigan 48824-1027, U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let V and W be two vector spaces over the field of real numbers R. Then we have the notion of the tensor product V ⊗ W. If V and W are inner product spaces with their inner products given respectively by «,»v and «,» w, then V ⊗ W is also an inner product space with inner product denned by

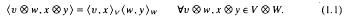
Let Em denote the m-dimensional Euclidean space with the canonical Euclidean inner product. Then, with respect to the inner product defined above, Em ⊗Em is isometric to Em. By applying this algebraic notion, we have the notion of tensor product mapf ⊗h: M→ E: M ⊗= Em; associated with any two maps f: M→Em and h:M→E of a given Riemannian manifold (M, g) defined as follows:

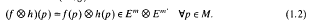
Denote by R(M) the set of all transversal immersions from an n-dimensional Riemannian manifold (M, g) into Euclidean spaces; i. e., immersions f:M→Em with f(p) ∉T*(TPM) for p ∈ M. Then ⊗ is a binary operation on R(M). Hence, if f: Mm and h: M→Em are immersions belonging to R(M), then their tensor product map f ⊗ h: M→ Em ⊗ Em ≡ Emm is an immersion in R(M), called the tensor product immersionof f and h.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 36 , Issue 2 , May 1994 , pp. 255 - 264
Copyright
Copyright © Glasgow Mathematical Journal Trust 1994

References

REFERENCES

1.Chen, B. Y., Geometry of submanifolds (M. Dekker, 1973).Google Scholar
2.Chen, B. Y., Total mean curvature and submanifolds of finite type (World Scientific, 1984).CrossRefGoogle Scholar
3.Chen, B. Y., Differential geometry of semirings of immersions, I: General theory. Bull. Inst. Math. Acad. Sinica 21 (1993), 1–34.Google Scholar
4.Dimitric, I., Quadric representation of a submanifold, Proc. Amer. Math. Soc. 114 (1992), 201–210.CrossRefGoogle Scholar
5.Ryan, P. J., Homogeneity and some curvature conditions for hypersurfaces, Tohoku Math. J. (2) 21 (1969), 363–388.CrossRefGoogle Scholar
6.Takahashi, T., Minimal immersions of Riemannian manifolds, J. Math. Soc. Japan 18 (1966), 380–385.CrossRefGoogle Scholar
7.Verstraelen, L., On submanifolds of finite Chen type and of restricted type, Results Math. 20 (1991), 744–755.CrossRefGoogle Scholar