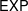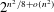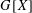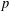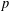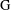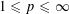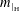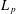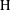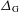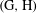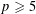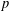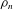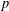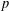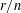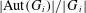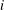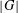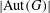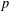Discrete Mathematics
Research Article
EIGENVALUES AND LINEAR QUASIRANDOM HYPERGRAPHS
- Part of:
-
- Published online by Cambridge University Press:
- 14 January 2015, e2
-
- Article
-
- You have access
- Open access
- Export citation
Differential Equations
Research Article
A CONTINUOUS INTERPOLATION BETWEEN CONSERVATIVE AND DISSIPATIVE SOLUTIONS FOR THE TWO-COMPONENT CAMASSA–HOLM SYSTEM
- Part of:
-
- Published online by Cambridge University Press:
- 07 January 2015, e1
-
- Article
-
- You have access
- Open access
- Export citation
Analysis
Research Article
LOCAL SET APPROXIMATION: MATTILA–VUORINEN TYPE SETS, REIFENBERG TYPE SETS, AND TANGENT SETS
- Part of:
-
- Published online by Cambridge University Press:
- 30 October 2015, e24
-
- Article
-
- You have access
- Open access
- Export citation
Number Theory
Research Article
TOPOLOGY ON COHOMOLOGY OF LOCAL FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 25 August 2015, e16
-
- Article
-
- You have access
- Open access
- Export citation
Computational Mathematics
Research Article
A THEORY OF COMPLEXITY, CONDITION, AND ROUNDOFF
- Part of:
-
- Published online by Cambridge University Press:
- 27 February 2015, e4
-
- Article
-
- You have access
- Open access
- Export citation
Discrete Mathematics
Research Article
THE TYPICAL STRUCTURE OF MAXIMAL TRIANGLE-FREE GRAPHS
- Part of:
-
- Published online by Cambridge University Press:
- 09 October 2015, e20
-
- Article
-
- You have access
- Open access
- Export citation
Number Theory
Research Article
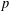 $p$-DIVISIBILITY FOR COHERENT COHOMOLOGY
$p$-DIVISIBILITY FOR COHERENT COHOMOLOGY
- Part of:
-
- Published online by Cambridge University Press:
- 13 August 2015, e15
-
- Article
-
- You have access
- Open access
- Export citation
Analysis
Research Article
NONCOMMUTATIVE DE LEEUW THEOREMS
- Part of:
-
- Published online by Cambridge University Press:
- 12 October 2015, e21
-
- Article
-
- You have access
- Open access
- Export citation
Differential Equations
Research Article
GROUP FOLIATION OF DIFFERENTIAL EQUATIONS USING MOVING FRAMES
- Part of:
-
- Published online by Cambridge University Press:
- 26 October 2015, e22
-
- Article
-
- You have access
- Open access
- Export citation
Algebra
Research Article
A REFINED WARING PROBLEM FOR FINITE SIMPLE GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 17 March 2015, e6
-
- Article
-
- You have access
- Open access
- Export citation
STABILITY PATTERNS IN REPRESENTATION THEORY
- Part of:
-
- Published online by Cambridge University Press:
- 15 June 2015, e11
-
- Article
-
- You have access
- Open access
- Export citation
THE DIMENSION OF A SUBCATEGORY OF MODULES
- Part of:
-
- Published online by Cambridge University Press:
- 09 October 2015, e19
-
- Article
-
- You have access
- Open access
- Export citation
Number Theory
Research Article
LIFTING TORSION GALOIS REPRESENTATIONS
-
- Published online by Cambridge University Press:
- 24 August 2015, e14
-
- Article
-
- You have access
- Open access
- Export citation
THE IWASAWA MAIN CONJECTURE FOR HILBERT MODULAR FORMS
- Part of:
-
- Published online by Cambridge University Press:
- 02 October 2015, e18
-
- Article
-
- You have access
- Open access
- Export citation
Algebra
Research Article
THE MOONSHINE MODULE FOR CONWAY’S GROUP
- Part of:
-
- Published online by Cambridge University Press:
- 15 June 2015, e10
-
- Article
-
- You have access
- Open access
- Export citation
Discrete Mathematics
Research Article
TRANSFERENCE FOR THE ERDŐS–KO–RADO THEOREM
- Part of:
-
- Published online by Cambridge University Press:
- 26 October 2015, e23
-
- Article
-
- You have access
- Open access
- Export citation
Algebra
Research Article
FINITE
 $p$-GROUPS WITH SMALL AUTOMORPHISM GROUP
$p$-GROUPS WITH SMALL AUTOMORPHISM GROUP
- Part of:
-
- Published online by Cambridge University Press:
- 20 April 2015, e7
-
- Article
-
- You have access
- Open access
- Export citation
Differential Equations
Research Article
UNIFORM BMO ESTIMATE OF PARABOLIC EQUATIONS AND GLOBAL WELL-POSEDNESS OF THE THERMISTOR PROBLEM
- Part of:
-
- Published online by Cambridge University Press:
- 02 December 2015, e26
-
- Article
-
- You have access
- Open access
- Export citation
Analysis
Research Article
THE MULTI-MARGINAL OPTIMAL PARTIAL TRANSPORT PROBLEM
- Part of:
-
- Published online by Cambridge University Press:
- 16 September 2015, e17
-
- Article
-
- You have access
- Open access
- Export citation
DYADIC TRIANGULAR HILBERT TRANSFORM OF TWO GENERAL FUNCTIONS AND ONE NOT TOO GENERAL FUNCTION
- Part of:
-
- Published online by Cambridge University Press:
- 13 November 2015, e25
-
- Article
-
- You have access
- Open access
- Export citation