Hostname: page-component-77c89778f8-7drxs Total loading time: 0 Render date: 2024-07-20T19:47:04.876Z Has data issue: false hasContentIssue false
  • English
  • Français

A THEORY OF COMPLEXITY, CONDITION, AND ROUNDOFF

Part of: Theory of computing

Published online by Cambridge University Press:  27 February 2015

FELIPE CUCKER
FELIPE CUCKER*
Affiliation:
Department of Mathematics, City University of Hong Kong, Hong Kong; macucker@cityu.edu.hk

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We develop a theory of complexity for numerical computations that takes into account the condition of the input data and allows for roundoff in the computations. We follow the lines of the theory developed by Blum, Shub and Smale for computations over 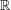$\mathbb{R}$ (which in turn followed those of the classical, discrete, complexity theory as laid down by Cook, Karp, and Levin, among others). In particular, we focus on complexity classes of decision problems and, paramount among them, on appropriate versions of the classes 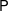$\mathsf{P}$, 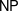$\mathsf{NP}$, and 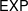$\mathsf{EXP}$ of polynomial, nondeterministic polynomial, and exponential time, respectively. We prove some basic relationships between these complexity classes, and provide natural NP-complete problems.

MSC classification

Primary: 68Q15: Complexity classes (hierarchies, relations among complexity classes, etc.)
Secondary: 68Q17: Computational difficulty of problems (lower bounds, completeness, difficulty of approximation, etc.)
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 3 , 2015 , e4
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/3.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author 2015

References

Allender, E., Bürgisser, P., Kjeldgaard-Pedersen, J. and Miltersen, P. B., ‘On the complexity of numerical analysis’, SIAM J. Comput. 38(5) (2008/09), 1987–2006.Google Scholar
Beltrán, C. and Pardo, L. M., ‘Smale’s 17th problem: average polynomial time to compute affine and projective solutions’, J. Amer. Math. Soc. 22(2) (2009), 363–385.Google Scholar
Beltrán, C. and Pardo, L. M., ‘Fast linear homotopy to find approximate zeros of polynomial systems’, Found. Comput. Math. 11(1) (2011), 95–129.Google Scholar
Blum, L., ‘Lectures on a theory of computation and complexity over the reals (or an arbitrary ring)’, in: Lectures in the Sciences of Complexity II (ed. Jen, E.) (Addison-Wesley, Redwood City, CA, 1990), 1–47.Google Scholar
Blum, L., Cucker, F., Shub, M. and Smale, S., Complexity and Real Computation (Springer, New York, 1998).Google Scholar
Blum, L., Shub, M. and Smale, S., ‘On a theory of computation and complexity over the real numbers: NP-completeness, recursive functions and universal machines’, Bull. Amer. Math. Soc. 21 (1989), 1–46.Google Scholar
Braverman, M. and Cook, S., ‘Computing over the reals: foundations for scientific computing’, Notices Amer. Math. Soc. 53(3) (2006), 318–329.Google Scholar
Bürgisser, P. and Cucker, F., ‘Exotic quantifiers, complexity classes, and complete problems’, Found. Comput. Math. 9 (2009), 135–170.Google Scholar
Bürgisser, P. and Cucker, F., ‘On a problem posed by Steve Smale’, Ann. Math. 174 (2011), 1785–1836.Google Scholar
Bürgisser, P. and Cucker, F., Condition, Grundlehren der mathematischen Wissenschaften, Vol. 349, (Springer, Berlin, 2013).Google Scholar
Bürgisser, P., Cucker, F. and Lotz, M., ‘Coverage processes on spheres and condition numbers for linear programming’, Ann. Probab. 38 (2010), 570–604.Google Scholar
Cheung, D. and Cucker, F., ‘A new condition number for linear programming’, Math. Program. 91 (2001), 163–174.Google Scholar
Cheung, D., Cucker, F. and Ye, Y., ‘Linear programming and condition numbers under the real number computation model’, in: Handbook of Numerical Analysis, Vol. XI (eds. Ciarlet, Ph. and Cucker, F.) (North-Holland, Amsterdam, 2003), 141–207.Google Scholar
Cobham, A., ‘The intrinsic computational difficulty of problems’, in: International Congress for Logic, Methodology, and the Philosophy of Science (ed. Bar-Hillel, Y.) (North-Holland, Amsterdam, 1964), 24–30.Google Scholar
Cook, S., ‘The complexity of theorem proving procedures’, in: 3rd Annual ACM Symposium on the Theory of Computing (Assoc. Comput. Mach., New York, 1971), 151–158.Google Scholar
Cook, S., ‘The P versus NP problem’, in: The Millennium Prize Problems (Clay Math. Inst., Cambridge, MA, 2006), 87–104.Google Scholar
Cucker, F., ‘Pℝ̸ = NCℝ’, J. Complexity 8 (1992), 230–238.Google Scholar
Cucker, F. and Koiran, P., ‘Computing over the reals with addition and order: higher complexity classes’, J. Complexity 11 (1995), 358–376.CrossRefGoogle Scholar
Cucker, F., Krick, T., Malajovich, G. and Wschebor, M., ‘A numerical algorithm for zero counting. I. Complexity and accuracy’, J. Complexity 24 (2008), 582–605.Google Scholar
Cucker, F., Krick, T., Malajovich, G. and Wschebor, M., ‘A numerical algorithm for zero counting. II. Distance to ill-posedness and smoothed analysis’, J. Fixed Point Theory Appl. 6 (2009), 285–294.Google Scholar
Cucker, F. and Peña, J., ‘A primal-dual algorithm for solving polyhedral conic systems with a finite-precision machine’, SIAM J. Optim. 12 (2002), 522–554.CrossRefGoogle Scholar
Cucker, F. and Smale, S., ‘Complexity estimates depending on condition and round-off error’, J. ACM 46 (1999), 113–184.Google Scholar
Cucker, F. and Torrecillas, A., ‘Two P-complete problems in the theory of the reals’, J. Complexity 8 (1992), 454–466.Google Scholar
Demmel, J., ‘On condition numbers and the distance to the nearest ill-posed problem’, Numer. Math. 51 (1987), 251–289.Google Scholar
Demmel, J. W., Applied Numerical Linear Algebra (SIAM, Philadelphia, PA, 1997).Google Scholar
Eckart, C. and Young, G., ‘The approximation of one matrix by another of lower rank’, Psychometrika 1 (1936), 211–218.Google Scholar
Edelman, A., ‘Eigenvalues and condition numbers of random matrices’, SIAM J. Matrix Anal. Appl. 9 (1988), 543–556.Google Scholar
Edmonds, J., ‘Paths, trees, and flowers’, Canad. J. Math. 17 (1965), 449–467.Google Scholar
Goffin, J.-L., ‘The relaxation method for solving systems of linear inequalities’, Math. Oper. Res. 5 (1980), 388–414.Google Scholar
Goldreich, O., Computational Complexity (Cambridge University Press, Cambridge, 2008), A conceptual perspective.Google Scholar
Hartmanis, J., Lewis, P. L. and Stearns, R. E., ‘Hierarchies of memory-limited computations’, in: 6th IEEE Symposium on Switching Circuit Theory and Logic Design (IEEE Comput. Soc., Long Beach, CA, 1965), 179–190.Google Scholar
Hartmanis, J. and Stearns, R. E., ‘On the computational complexity of algorithms’, Trans. Amer. Math. Soc. 117 (1965), 285–306.CrossRefGoogle Scholar
Heintz, J., Roy, M.-F. and Solerno, P., ‘Sur la complexité du principe de Tarski–Seidenberg’, Bull. Soc. Math. France 118 (1990), 101–126.Google Scholar
Hestenes, M. R. and Stiefel, E., ‘Methods of conjugate gradients for solving linear systems’, J. Research Nat. Bur. Standards 49(1953) (1952), 409–436.Google Scholar
Higham, N., Accuracy and Stability of Numerical Algorithms (SIAM, Philadelphia, PA, 1996).Google Scholar
Homer, S. and Selman, A. L., Computability and complexity theory, second edn, Texts in Computer Science, (Springer, New York, 2011).Google Scholar
Karp, R. M., ‘Reducibility among combinatorial problems’, in: Complexity of Computer Computations (eds. Miller, R. and Thatcher, J.) (Plenum Press, 1972), 85–103.Google Scholar
Ko, K.-I., Complexity Theory of Real Functions, Progress in Theoretical Computer Science, (Birkhäuser Boston, Inc., Boston, MA, 1991).Google Scholar
Koiran, P., ‘Computing over the reals with addition and order’, Theor. Comput. Sci. 133 (1994), 35–47.Google Scholar
Ladner, R. E., ‘The circuit value problem is log space complete for ℙ’, SIGACT News 7 (1975), 18–20.Google Scholar
Levin, L., ‘Universal sequential search problems’, Probl. Pered. Inform. IX 3 (1973), 265–266. (in Russian), (English translation in Problems of Information Trans. 9, 3; corrected translation in [58]).Google Scholar
Miller, W., ‘Computational complexity and numerical stability’, SIAM J. Comput. 4 (1975), 97–107.CrossRefGoogle Scholar
Papadimitriou, C. H., Computational Complexity (Addison-Wesley, Redwood City, CA, 1994).Google Scholar
Poizat, B., Les Petits Cailloux (Aléa, Paris, 1995).Google Scholar
Renegar, J., ‘On the computational complexity and geometry of the first-order theory of the reals. Part I’, J. Symbolic Comput. 13 (1992), 255–299.Google Scholar
Renegar, J., ‘Is it possible to know a problem instance is ill-posed?’, J. Complexity 10 (1994), 1–56.Google Scholar
Renegar, J., ‘Some perturbation theory for linear programming’, Math. Program. 65 (1994), 73–91.Google Scholar
Renegar, J., ‘Incorporating condition measures into the complexity theory of linear programming’, SIAM J. Optim. 5 (1995), 506–524.Google Scholar
Renegar, J., ‘Linear programming, complexity theory and elementary functional analysis’, Math. Program. 70 (1995), 279–351.Google Scholar
Shub, M. and Smale, S., ‘Complexity of Bézout’s Theorem I: geometric aspects’, J. Amer. Math. Soc. 6 (1993), 459–501.Google Scholar
Shub, M. and Smale, S., ‘Complexity of Bézout’s Theorem II: volumes and probabilities’, in: Computational Algebraic Geometry, (eds. Eyssette, F. and Galligo, A.) Progress in Mathematics, Vol. 109 (Birkhäuser, Basel, 1993), 267–285.Google Scholar
Shub, M. and Smale, S., ‘Complexity of Bézout’s Theorem III: condition number and packing’, J. Complexity 9 (1993), 4–14.Google Scholar
Shub, M. and Smale, S., ‘Complexity of Bézout’s Theorem IV: probability of success; extensions’, SIAM J. Numer. Anal. 33 (1996), 128–148.Google Scholar
Shub, M. and Smale, S., ‘Complexity of Bézout’s Theorem V: polynomial time’, Theor. Comput. Sci. 133 (1994), 141–164.Google Scholar
Smale, S., ‘Some remarks on the foundations of numerical analysis’, SIAM Rev. 32 (1990), 211–220.Google Scholar
Smale, S., ‘Complexity theory and numerical analysis’, in: Acta Numerica (ed. Iserles, A.) (Cambridge University Press, Cambridge, UK, 1997), 523–551.Google Scholar
Smale, S., ‘Mathematical problems for the next century’, in: Mathematics: Frontiers and Perspectives (eds. Arnold, V., Atiyah, M., Lax, P. and Mazur, B.) (American Mathematical Society, Providence, RI, 2000), 271–294.Google Scholar
Trakhtenbrot, B. A., ‘A survey of russian approaches to perebor (brute-force search) algorithms’, Ann. Hist. Comput. 6 (1984), 384–400.Google Scholar
Turing, A. M., ‘Rounding-off errors in matrix processes’, Quart. J. Mech. Appl. Math. 1 (1948), 287–308.CrossRefGoogle Scholar
von Neumann, J. and Goldstine, H. H., ‘Numerical inverting matrices of high order’, Bull. Amer. Math. Soc. 53 (1947), 1021–1099.CrossRefGoogle Scholar
von Neumann, J. and Goldstine, H. H., ‘Numerical inverting matrices of high order, II’, Proc. Amer. Math. Soc. 2 (1951), 188–202.Google Scholar
Weihrauch, K., Computable Analysis, Texts in Theoretical Computer Science. An EATCS Series, (Springer, Berlin, 2000).Google Scholar
Wilkinson, J., ‘Some comments from a numerical analyst’, J. ACM 18 (1971), 137–147.Google Scholar