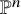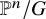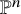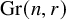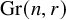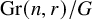Introduction
In the most famous and fundamental of examples of mirror symmetry, the Fermat hypersurface in
![]() $\mathbb {P}^{n-1}$
mirrors the Fermat hypersurface in a finite group quotient of
$\mathbb {P}^{n-1}$
mirrors the Fermat hypersurface in a finite group quotient of
![]() $\mathbb {P}^{n-1}$
. The action of the finite group on
$\mathbb {P}^{n-1}$
. The action of the finite group on
![]() $\mathbb {P}^{n-1}$
is obtained by the action of the group
$\mathbb {P}^{n-1}$
is obtained by the action of the group
which is identified with a subgroup of the diagonal matrices of
![]() $\operatorname {{\mathrm {SL}}}({\mathbb {C}}^n)$
and hence acts naturally on
$\operatorname {{\mathrm {SL}}}({\mathbb {C}}^n)$
and hence acts naturally on
![]() ${\mathbb {C}}^n$
. This descends to an action on the geometric invariant theory (GIT) quotient
${\mathbb {C}}^n$
. This descends to an action on the geometric invariant theory (GIT) quotient
![]() ${\mathbb {C}}^n/\!/{\mathbb {C}}^*=\mathbb {P}^{n-1}$
; we let
${\mathbb {C}}^n/\!/{\mathbb {C}}^*=\mathbb {P}^{n-1}$
; we let
![]() $H_{n,1}$
denote the quotient group of
$H_{n,1}$
denote the quotient group of
![]() $\tilde {H}_{n,1}$
that acts effectively on
$\tilde {H}_{n,1}$
that acts effectively on
![]() $\mathbb {P}^{n-1}$
. The Fermat hypersurface in
$\mathbb {P}^{n-1}$
. The Fermat hypersurface in
![]() $\mathbb {P}^{n-1}$
is mirror to the Fermat hypersurface in
$\mathbb {P}^{n-1}$
is mirror to the Fermat hypersurface in
![]() $\mathbb {P}^{n-1}/H_{n,1}$
. This is the first in a series of examples appearing in Greene–Plesser [Reference Greene and Plesser11].
$\mathbb {P}^{n-1}/H_{n,1}$
. This is the first in a series of examples appearing in Greene–Plesser [Reference Greene and Plesser11].
In this paper, we explore the analogue of Greene–Plesser mirror symmetry for Grassmannians. The Grassmannian of quotients can be constructed as a GIT quotient
![]() $\operatorname {{\mathrm {Mat}}}(r \times n)/\!/\operatorname {{\mathrm {GL}}}(r)$
. The group
$\operatorname {{\mathrm {Mat}}}(r \times n)/\!/\operatorname {{\mathrm {GL}}}(r)$
. The group
is identified with a subgroup of the diagonal matrices in
![]() $\operatorname {{\mathrm {GL}}}({\mathbb {C}}^n)$
, which acts on
$\operatorname {{\mathrm {GL}}}({\mathbb {C}}^n)$
, which acts on
![]() $\operatorname {{\mathrm {Mat}}}(r\times n)$
by multiplication on the right. It can also be identified with a subgroup in
$\operatorname {{\mathrm {Mat}}}(r\times n)$
by multiplication on the right. It can also be identified with a subgroup in
![]() $\operatorname {{\mathrm {SL}}}(\operatorname {{\mathrm {Mat}}}(r\times n))$
acting on
$\operatorname {{\mathrm {SL}}}(\operatorname {{\mathrm {Mat}}}(r\times n))$
acting on
![]() $\operatorname {{\mathrm {Mat}}}(r \times n)$
as a vector space—it is in this sense that the
$\operatorname {{\mathrm {Mat}}}(r \times n)$
as a vector space—it is in this sense that the
![]() $(\prod \zeta _i)^r=1$
is a determinant
$(\prod \zeta _i)^r=1$
is a determinant
![]() $1$
condition. The action of
$1$
condition. The action of
![]() $\tilde {H}_{n,r}$
descends to an action on
$\tilde {H}_{n,r}$
descends to an action on
![]() $\operatorname {{\mathrm {Gr}}}(n,r)$
; we let
$\operatorname {{\mathrm {Gr}}}(n,r)$
; we let
![]() $H_{n,r}$
denote the quotient of
$H_{n,r}$
denote the quotient of
![]() $\tilde {H}_{n,r}$
that acts effectively on
$\tilde {H}_{n,r}$
that acts effectively on
![]() $\operatorname {{\mathrm {Gr}}}(n,r)$
.
$\operatorname {{\mathrm {Gr}}}(n,r)$
.
We relate
![]() $\operatorname {{\mathrm {Gr}}}(n,r)$
and
$\operatorname {{\mathrm {Gr}}}(n,r)$
and
![]() $\operatorname {{\mathrm {Gr}}}(n,r)/{H}_{n,r}$
via mirror symmetry, although—as suits the Grassmannian—the story is richer and more complex, involving not just mirror duality but also toric degenerations, a variation of polytope duality, blow-ups and variations of GIT. In unpacking this picture, we also provide a compactification of the fibers of the Eguchi–Hori–Xiong [Reference Eguchi, Hori and Xiong9] mirror of the Grassmannian. With a bit of notation, we can state the main result.
$\operatorname {{\mathrm {Gr}}}(n,r)/{H}_{n,r}$
via mirror symmetry, although—as suits the Grassmannian—the story is richer and more complex, involving not just mirror duality but also toric degenerations, a variation of polytope duality, blow-ups and variations of GIT. In unpacking this picture, we also provide a compactification of the fibers of the Eguchi–Hori–Xiong [Reference Eguchi, Hori and Xiong9] mirror of the Grassmannian. With a bit of notation, we can state the main result.
Let P be a lattice polytope and
![]() $P^{\vee }$
its dual. The variety
$P^{\vee }$
its dual. The variety
![]() $X_P$
is the toric variety built from the spanning fan of P. Mirror pairs of Calabi–Yau hypersurfaces come from pairs of toric varieties
$X_P$
is the toric variety built from the spanning fan of P. Mirror pairs of Calabi–Yau hypersurfaces come from pairs of toric varieties
![]() $X_P, X_{P^{\vee }}$
. We define the primitive dual of a toric variety
$X_P, X_{P^{\vee }}$
. We define the primitive dual of a toric variety
![]() $X_P$
as
$X_P$
as
![]() $X_Q$
, where Q is the dual polytope of P viewed in the lattice spanned by its vertices (see Definition 1.3). The primitive dual of
$X_Q$
, where Q is the dual polytope of P viewed in the lattice spanned by its vertices (see Definition 1.3). The primitive dual of
![]() $\mathbb {P}^{n-1}$
is itself: This explains the reappearance of
$\mathbb {P}^{n-1}$
is itself: This explains the reappearance of
![]() $\mathbb {P}^{n-1}$
(albeit with a group action) under mirror duality.
$\mathbb {P}^{n-1}$
(albeit with a group action) under mirror duality.
In [Reference Gonciulea and Lakshmibai10], Gonciulea and Lakshmibai describe a toric degeneration of the Grassmannian to the toric variety associated to a Gelfand–Cetlin polytope. We call this the Gelfand–Cetlin toric degeneration.
Theorem 0.1 (Theorem 4.16)
Let
![]() $X_P$
be the special fiber of the Gelfand–Cetlin toric degeneration, and
$X_P$
be the special fiber of the Gelfand–Cetlin toric degeneration, and
![]() $X_Q$
its primitive dual. Then there is a smoothing of the Batyrev–Borisov dual
$X_Q$
its primitive dual. Then there is a smoothing of the Batyrev–Borisov dual
![]() $X_{Q^{\vee }}$
of
$X_{Q^{\vee }}$
of
![]() $X_Q$
to
$X_Q$
to
![]() $\operatorname {{\mathrm {Gr}}}(n,r)/H_{n,r}$
.
$\operatorname {{\mathrm {Gr}}}(n,r)/H_{n,r}$
.
The geometry relating
![]() $X_P$
and
$X_P$
and
![]() $X_Q$
can be further described.
$X_Q$
can be further described.
Theorem 0.2 (Theorem 3.7)
There is a toric blow-up of
![]() $X_P$
that can be obtained from
$X_P$
that can be obtained from
![]() $X_Q$
by a crepant toric variation of GIT. The reverse holds for their Batyrev–Borisov duals: There is a toric blow-up of
$X_Q$
by a crepant toric variation of GIT. The reverse holds for their Batyrev–Borisov duals: There is a toric blow-up of
![]() $X_{Q^{\vee }}$
that can be obtained from
$X_{Q^{\vee }}$
that can be obtained from
![]() $X_{P^{\vee }}$
by a crepant toric variation of GIT.
$X_{P^{\vee }}$
by a crepant toric variation of GIT.
The first proposals of mirror symmetry for Grassmannians arise in physics: Hori–Vafa [Reference Hori and Vafa13] and Eguchi–Hori–Xiong [Reference Eguchi, Hori and Xiong9]. Hori–Vafa’s proposal is rooted in the abelian/nonabelian correspondence (later further developed in [Reference Ciocan-Fontanine, Kim and Sabbah4, Reference Gu and Sharpe12]), while the Eguchi–Hori–Xiong construction can be seen to arise from the Gelfand–Cetlin toric degeneration [Reference Batyrev, Ciocan-Fontanine, Kim and van Straten3]. Another more recent proposal is the Marsh–Rietsch Plücker coordinate mirror [Reference Marsh and Rietsch18], which—very roughly speaking—is a mirror produced by combining the mirrors obtained through many toric degenerations arising from the cluster structure of the coordinate ring of the Grassmannian. These proposals focus on a Landau–Ginzburg model, or a superpotential, for the Grassmannian, where the story is much more developed, rather than on producing mirror partners for Calabi–Yau hypersurfaces in Grassmannians.
Both the abelian/nonabelian correspondence and toric degenerations essentially reduce the question of the mirror symmetry to the toric situation, where older results can be applied. The mirror constructed for Calabi–Yau hypersurfaces in Grassmannians in [Reference Batyrev, Ciocan-Fontanine, Kim and van Straten2] is of this form—they suggest a specialization of the mirror family obtained via applying the Batyrev–Borisov construction to the Gelfand–Cetlin toric degeneration. One problem, though, is that it is unclear how to reverse this process on the mirror side—how can we leave the toric context?
In this paper, we suggest a solution to this problem. The two theorems above suggest a possible mirror to the Fermat Calabi–Yau hypersurface of the Grassmannian, which we describe in equation (2) after establishing more notation. As in [Reference Batyrev, Ciocan-Fontanine, Kim and van Straten2], our proposal requires the Gelfand–Cetlin toric degeneration: We use its combinatorial structure to unwind the toric degeneration, arriving at a hypersurface in a quotient of a blow-up of the Grassmannian. The theorem below gives some evidence towards this proposal.
Theorem 0.3 (Theorem 5.4)
The fiber of the Eguchi–Hori–Xiong Laurent polynomial mirror to the Grassmannian compactifies to an anticanonical hypersurface cut out by equation (2) in a blow-up of the Grassmannian modulo the group
![]() $H_{n,r}$
.
$H_{n,r}$
.
While the construction here heavily uses the Gelfand–Cetlin toric degeneration, the final answer does not depend on the degeneration. It is therefore an intriguing question as to how this proposal fits in with the results of Marsh–Rietsch [Reference Marsh and Rietsch18] and Rietsch–Williams [Reference Rietsch and Williams21].
Overview of results
We now outline the results of the paper. The first step is a close study of the Batyrev–Borisov mirror of the Gelfand–Cetlin toric degeneration of the Grassmannian. We begin by looking at Batyrev–Borisov mirror symmetry for Fano toric varieties with high Fano index.
High index Fano varieties, lattices and Batyrev–Borisov mirror symmetry
Let P be a lattice polytope in a lattice N, and let M be the dual lattice. As before, we denote the toric variety arising from the spanning fan P as
![]() $X_P$
. If P is the polytope of projective space, that is, if
$X_P$
. If P is the polytope of projective space, that is, if
![]() $X_{P}=\mathbb {P}^n$
, then
$X_{P}=\mathbb {P}^n$
, then
![]() $X_{P^{\vee }}$
is just
$X_{P^{\vee }}$
is just
![]() $X_P/G$
, where
$X_P/G$
, where
![]() $G=(\mathbb {Z}/(n+1)\mathbb {Z})^{n-1}$
. The group action can be seen to arise from the fact that
$G=(\mathbb {Z}/(n+1)\mathbb {Z})^{n-1}$
. The group action can be seen to arise from the fact that
![]() $\mathbb {P}^n$
has Fano index
$\mathbb {P}^n$
has Fano index
![]() $n+1$
: The vertices of
$n+1$
: The vertices of
![]() $P^{\vee }$
span a sublattice
$P^{\vee }$
span a sublattice
![]() $i:\overline {M} \to M$
such that
$i:\overline {M} \to M$
such that
![]() $M /\overline {M} \cong G$
. The fact that
$M /\overline {M} \cong G$
. The fact that
![]() $X_{P^{\vee }}=\mathbb {P}^{n}/G$
is a consequence of the fact that
$X_{P^{\vee }}=\mathbb {P}^{n}/G$
is a consequence of the fact that
![]() $i^{-1}(P^{\vee }) =P$
.
$i^{-1}(P^{\vee }) =P$
.
It is a simple corollary of the Batyrev–Borisov construction that if we take intermediate lattices we recover Greene–Plesser mirror symmetry for the Calabi–Yau hypersurface in projective space. Consider a lattice inclusion
![]() $\overline {M} \subset M' \subset M$
, and set
$\overline {M} \subset M' \subset M$
, and set
![]() $(M')^{\vee }=N'$
and
$(M')^{\vee }=N'$
and
![]() $\overline {M}^{\vee }=\overline {N}$
. Then the anticanonical hypersurface in
$\overline {M}^{\vee }=\overline {N}$
. Then the anticanonical hypersurface in
![]() $\mathbb {P}^n/(N'/N)$
forms a mirror pair with the anticanonical hypersurface in
$\mathbb {P}^n/(N'/N)$
forms a mirror pair with the anticanonical hypersurface in
![]() $\mathbb {P}^n/(M'/\overline {M}).$
$\mathbb {P}^n/(M'/\overline {M}).$
We show in §1 that there is an analogous picture for any Fano toric variety of index n. Let P be a reflexive Fano polytope of Fano index k. The vertices of
![]() $P^{\vee }$
span a sublattice
$P^{\vee }$
span a sublattice
![]() $i:\overline {N} \to N$
. Set
$i:\overline {N} \to N$
. Set
![]() $G:=N/\overline {N}$
. In the projective space example above and in many other cases,
$G:=N/\overline {N}$
. In the projective space example above and in many other cases,
![]() $ G \cong (\mathbb {Z}/k\mathbb {Z})^{\dim X_P-1}$
. Let Q denote the polytope
$ G \cong (\mathbb {Z}/k\mathbb {Z})^{\dim X_P-1}$
. Let Q denote the polytope
![]() $i^{-1}(P)$
. Then mirror symmetry reverses the roles of P and Q:
$i^{-1}(P)$
. Then mirror symmetry reverses the roles of P and Q:

where the arrows are Batyrev–Borisov mirror symmetry. We call Q the primitive dual of P. For polytopes whose vertices generate the ambient lattice, this is a duality. We also obtain a series of mirror pairs via considering intermediate lattices.
Proposition 0.4. Given lattice inclusions
![]() $\overline {N} \subset N' \subset N$
, dualizing to
$\overline {N} \subset N' \subset N$
, dualizing to
![]() $M \subset M' \subset \overline {M}$
, the toric varieties
$M \subset M' \subset \overline {M}$
, the toric varieties
![]() $X_P/(N/N')$
and
$X_P/(N/N')$
and
![]() $X_Q/(M'/\overline {M})$
are a Batyrev–Borisov mirror pair.
$X_Q/(M'/\overline {M})$
are a Batyrev–Borisov mirror pair.
If
![]() $X_P$
is a sufficiently nice toric degeneration of the Grassmannian, then it is in particular a Fano variety of Fano index n. If
$X_P$
is a sufficiently nice toric degeneration of the Grassmannian, then it is in particular a Fano variety of Fano index n. If
![]() $X_P$
is the Gelfand–Cetlin toric degeneration, then its vertices can be described via a ladder diagram ([Reference Batyrev, Ciocan-Fontanine, Kim and van Straten3]; see §2). The primitive dual Q can be described via the same diagram. We give a description of Q in this case in §2.
$X_P$
is the Gelfand–Cetlin toric degeneration, then its vertices can be described via a ladder diagram ([Reference Batyrev, Ciocan-Fontanine, Kim and van Straten3]; see §2). The primitive dual Q can be described via the same diagram. We give a description of Q in this case in §2.
The series of examples of mirror pairs for projective space includes the quintic twin [Reference Doran and Morgan8], which intriguingly has the same Picard–Fuchs equations as the quintic. The perspective in this paper, allows us to generalize this ‘twin phenomenon’ to toric degenerations of the Grassmannian. See §2.4.
The Gelfand–Cetlin toric degeneration and variation of geometric invariant theory quotient
Let
![]() $P_{n,r}$
denote the reflexive Fano polytope associated to the Gelfand–Cetlin toric degeneration, and
$P_{n,r}$
denote the reflexive Fano polytope associated to the Gelfand–Cetlin toric degeneration, and
![]() $Q_{n,r}$
its primitive dual. Let
$Q_{n,r}$
its primitive dual. Let
![]() $G_{n,r}:=(\mathbb {Z}/n\mathbb {Z})^{r(n-r)-1}.$
The polytopes
$G_{n,r}:=(\mathbb {Z}/n\mathbb {Z})^{r(n-r)-1}.$
The polytopes
![]() $P_{n,r}$
and
$P_{n,r}$
and
![]() $Q_{n,r}$
are closely related via mirror symmetry, but in fact there is another relation. The main result of §3 is Theorem 0.2: There is a weak Fano toric variety
$Q_{n,r}$
are closely related via mirror symmetry, but in fact there is another relation. The main result of §3 is Theorem 0.2: There is a weak Fano toric variety
![]() $Y_{n,r}$
that fits into the diagram
$Y_{n,r}$
that fits into the diagram

Note that, under mirror symmetry, the roles of the two maps in the diagram are reversed, suggesting the relationship is analogous to a geometric transition. The variation of GIT is a toric variation of GIT. While it is not a crepant resolution, the variation of geometric invariant theory quotient (VGIT) is a K-equivalence: It preserves the anticanonical class in the sense that the polyhedron associated to the anticanonical divisor is the same for each toric variety.
Smoothing
In the first subsection of §4, we prove Theorem 0.1 above, which we can now state more precisely. There is a natural embedding of
![]() $X_{P_{n,r}}$
into
$X_{P_{n,r}}$
into
![]() $\mathbb {P}^{\binom {n}{r}-1}$
, and it is in
$\mathbb {P}^{\binom {n}{r}-1}$
, and it is in
![]() $\mathbb {P}^{\binom {n}{r}-1}$
that the Gelfand–Cetlin toric degeneration is seen. The embedding allows G to act not just on
$\mathbb {P}^{\binom {n}{r}-1}$
that the Gelfand–Cetlin toric degeneration is seen. The embedding allows G to act not just on
![]() $X_{P_{n,r}}$
but on the whole projective space. The heart of the theorem is the remarkable characterization of
$X_{P_{n,r}}$
but on the whole projective space. The heart of the theorem is the remarkable characterization of
![]() $H_{n,r}$
as precisely the maximal subgroup of G for which the Grassmannian is an equivariant subvariety (see Theorem 4.9).
$H_{n,r}$
as precisely the maximal subgroup of G for which the Grassmannian is an equivariant subvariety (see Theorem 4.9).
It is easy to construct a G-equivariant family
![]() $Z \subset \mathbb {P}^{\binom {n}{r}-1} \times {\mathbb {C}}^m$
, with coefficients
$Z \subset \mathbb {P}^{\binom {n}{r}-1} \times {\mathbb {C}}^m$
, with coefficients
![]() $c_i$
on the second factor, such that the special fiber is
$c_i$
on the second factor, such that the special fiber is
![]() $X_{P_{n,r}}$
and the general fiber is
$X_{P_{n,r}}$
and the general fiber is
![]() $\operatorname {{\mathrm {Gr}}}(n,r)$
. This is just the Gelfand–Cetlin toric degeneration, where we extend the action of G to the second factor in such a way that the varying Plücker relations are G-invariant. To obtain a smoothing of
$\operatorname {{\mathrm {Gr}}}(n,r)$
. This is just the Gelfand–Cetlin toric degeneration, where we extend the action of G to the second factor in such a way that the varying Plücker relations are G-invariant. To obtain a smoothing of
![]() $X_{P_{n,r}}/G$
, we need to take the quotient of this family by G. Fibers of the quotient family are
$X_{P_{n,r}}/G$
, we need to take the quotient of this family by G. Fibers of the quotient family are
for constants
![]() $b_i$
.
$b_i$
.
Theorem 0.5. The generic fiber of the quotient family is isomorphic to
![]() $\operatorname {{\mathrm {Gr}}}(n,r)/H_{n,r}$
.
$\operatorname {{\mathrm {Gr}}}(n,r)/H_{n,r}$
.
We call this a smoothing, as the only singularities arise from the finite group quotient.
We also describe a partial smoothing of
![]() $Y_{n,r}$
. Using the characterization of
$Y_{n,r}$
. Using the characterization of
![]() $Y_{n,r}$
as the blow-up of the Gelfand–Cetlin degeneration, one can write down binomial equations cutting
$Y_{n,r}$
as the blow-up of the Gelfand–Cetlin degeneration, one can write down binomial equations cutting
![]() $Y_{n,r}$
out of an ambient space obtained by blowing-up
$Y_{n,r}$
out of an ambient space obtained by blowing-up
![]() $\mathbb {P}^{\binom {n}{r}-1}$
multiple times. This description allows us to reverse the Gelfand–Cetlin degeneration to (partially) smooth to the proper transform of the Grassmannian in the blow-up. We call the resulting variety
$\mathbb {P}^{\binom {n}{r}-1}$
multiple times. This description allows us to reverse the Gelfand–Cetlin degeneration to (partially) smooth to the proper transform of the Grassmannian in the blow-up. We call the resulting variety
![]() $\operatorname {{\mathrm {Bl}}} \operatorname {{\mathrm {Gr}}}(n,r)$
.
$\operatorname {{\mathrm {Bl}}} \operatorname {{\mathrm {Gr}}}(n,r)$
.
Our mirror proposal
Consider the equations
 $$ \begin{align} \sum_{\lambda \in {\mathcal{A}(n,r)}} p_{\lambda}^n + \psi \prod_{p_{\mu} \text{ frozen}}p_{\mu}=0. \end{align} $$
$$ \begin{align} \sum_{\lambda \in {\mathcal{A}(n,r)}} p_{\lambda}^n + \psi \prod_{p_{\mu} \text{ frozen}}p_{\mu}=0. \end{align} $$
The product in the second term is over frozen Plücker coordinates which are indexed by partitions
![]() $\mu $
which are maximal rectangular partitions. For details and definitions, see §5. This equation defines a family of Calabi–Yau hypersurfaces in
$\mu $
which are maximal rectangular partitions. For details and definitions, see §5. This equation defines a family of Calabi–Yau hypersurfaces in
![]() $\operatorname {{\mathrm {Bl}}} \operatorname {{\mathrm {Gr}}}(n,r)/{H}$
. This is a candidate mirror to a Calabi–Yau hypersurface in
$\operatorname {{\mathrm {Bl}}} \operatorname {{\mathrm {Gr}}}(n,r)/{H}$
. This is a candidate mirror to a Calabi–Yau hypersurface in
![]() $\operatorname {{\mathrm {Gr}}}(n,r)$
. In §5, we give evidence towards this conjecture by showing Theorem 0.3 above.
$\operatorname {{\mathrm {Gr}}}(n,r)$
. In §5, we give evidence towards this conjecture by showing Theorem 0.3 above.
Plan of the paper
In §1, we explain the special behaviour exhibited by high index Fano varieties under Batyrev–Borisov mirror symmetry and introduce primitive duality. In §2, we specialize to the Gelfand–Cetlin toric degeneration and describe the combinatorics of
![]() $P_{n,r}$
and
$P_{n,r}$
and
![]() $Q_{n,r}$
. In §3, we describe the geometry relating
$Q_{n,r}$
. In §3, we describe the geometry relating
![]() $X_{P_{n,r}}$
and
$X_{P_{n,r}}$
and
![]() $X_{Q_{n,r}}$
. In §4, we describe how to ‘unwind’ the toric degenerations after mirror symmetry: We give smoothings for
$X_{Q_{n,r}}$
. In §4, we describe how to ‘unwind’ the toric degenerations after mirror symmetry: We give smoothings for
![]() $Y_{n,r}/G$
and
$Y_{n,r}/G$
and
![]() $X_{P_{n,r}}/G$
. In §5, we introduce a candidate mirror of the anticanonical Fermat Calabi–Yau in the Grassmannian.
$X_{P_{n,r}}/G$
. In §5, we introduce a candidate mirror of the anticanonical Fermat Calabi–Yau in the Grassmannian.
1 Lattices and Batyrev–Borisov mirror symmetry
In this first section, we explore Batyrev–Borisov mirror symmetry for Calabi–Yau hypersurfaces in high index Fano toric varieties. In this paper, we’ll only consider mirror symmetry for Calabi–Yau hypersurfaces rather than complete intersections, so this amounts just to duality of reflexive polytopes. We thus refer to
![]() $X_{P^{\vee }}$
as the Batyrev–Borisov dual of
$X_{P^{\vee }}$
as the Batyrev–Borisov dual of
![]() $X_P$
, where P is a reflexive polytope.
$X_P$
, where P is a reflexive polytope.
1.1 Background on toric varieties
1.1.1 Reflexive polytopes
Let P be a full-dimensional lattice polytope in a lattice M, containing the origin in its strict interior. Let
![]() $N=M^{\vee }$
be the dual lattice. The dual of P is
$N=M^{\vee }$
be the dual lattice. The dual of P is
Definition 1.1. A polytope P is reflexive if
![]() $P^{\vee }$
is also a lattice polytope.
$P^{\vee }$
is also a lattice polytope.
Vertices of reflexive polytopes are primitive lattice vectors.
Definition 1.2. A lattice polytope
![]() $P \subset M_{\mathbb {R}}$
is vertex spanning if the set of vertices of P span the lattice M.
$P \subset M_{\mathbb {R}}$
is vertex spanning if the set of vertices of P span the lattice M.
Reflexive polytopes may or may not be vertex spanning. For example, among the 4,319 three-dimensional reflexive polytopes, classified in [Reference Kreuzer and Skarke16], 4,075 are vertex spanning and 244 are not.
1.1.2 Toric varieties from reflexive polytopes
Let P be a reflexive polytope, and let F be the spanning fan of P. Then a toric variety
![]() $X_P$
can be constructed in the usual way from F. We say that this is toric variety associated to P (that is, our convention uses spanning rather than normal fans).
$X_P$
can be constructed in the usual way from F. We say that this is toric variety associated to P (that is, our convention uses spanning rather than normal fans).
1.1.3 Toric varieties from weights
In addition to polytopes and fans, toric varieties can also be constructed using GIT data. The GIT data for a toric variety is
-
1. A torus
 $K \cong ({\mathbb {C}}^*)^r$
,
$K \cong ({\mathbb {C}}^*)^r$
, -
2. Weights
 $D_1,\dots ,D_m$
of K defining an action K on
$D_1,\dots ,D_m$
of K defining an action K on
 ${\mathbb {C}}^m$
,
${\mathbb {C}}^m$
, -
3. A stability condition
 $\omega $
, which is a co-character of K.
$\omega $
, which is a co-character of K.
The toric variety
![]() $X_{\omega }$
is then the GIT quotient
$X_{\omega }$
is then the GIT quotient
![]() ${\mathbb {C}}^m/\!\!/_{\omega } K$
. For a description of how to pass between the GIT description of a toric variety and the fan construction, see, for example, [Reference Coates, Iritani and Jiang6, Section 4].
${\mathbb {C}}^m/\!\!/_{\omega } K$
. For a description of how to pass between the GIT description of a toric variety and the fan construction, see, for example, [Reference Coates, Iritani and Jiang6, Section 4].
1.1.4 Toric divisors
Let F be a fan in a lattice N, and let X denote the toric variety defined by F. A toric divisor D on X defines a polyhedron
![]() $P_D$
in
$P_D$
in
![]() $M_{\mathbb {R}}$
, where
$M_{\mathbb {R}}$
, where
![]() $M = N^{\vee }$
; see, for example, [Reference Cox, Little and Schenck7, Chapter 5]. This association between toric divisors and polyhedra has the properties that:
$M = N^{\vee }$
; see, for example, [Reference Cox, Little and Schenck7, Chapter 5]. This association between toric divisors and polyhedra has the properties that:
-
○ the polyhedron for
 $n D$
is
$n D$
is
 $n P_D$
; and
$n P_D$
; and -
○ if two divisors are linearly equivalent then their polyhedra are translates of each other.
By definition of duality, if P is a reflexive polytope, then
![]() $P_{-K_{X_P}}=P^{\vee }$
, where
$P_{-K_{X_P}}=P^{\vee }$
, where
![]() ${-K}_{X_P}$
is the anticanonical divisor given by the sum of the toric divisors on
${-K}_{X_P}$
is the anticanonical divisor given by the sum of the toric divisors on
![]() $X_P$
.
$X_P$
.
1.2 High-index Fano varieties
Throughout this section, we will fix a d-dimensional reflexive Fano polytope P giving rise (via the spanning fan) to a Fano toric variety
![]() $X_P$
. We assume that
$X_P$
. We assume that
![]() $X_P$
has Fano index n. Let N denote the ambient lattice of P and M the dual lattice.
$X_P$
has Fano index n. Let N denote the ambient lattice of P and M the dual lattice.
Let
![]() $\overline {M}$
be the sublattice of M spanned by the vertices of
$\overline {M}$
be the sublattice of M spanned by the vertices of
![]() $P_{-K_{X_P}}$
. Let Q denote the lattice polytope in
$P_{-K_{X_P}}$
. Let Q denote the lattice polytope in
![]() $\overline {M}$
given by the preimage of
$\overline {M}$
given by the preimage of
![]() $P_{-K_{X_P}}$
under the inclusion
$P_{-K_{X_P}}$
under the inclusion
![]() $\overline {M} \subset M$
.
$\overline {M} \subset M$
.
Definition 1.3. The polytope Q is the primitive dual of P.
Remark 1.4. The primitive dual of a reflexive polytope is a reflexive polytope.
Example 1.5. The polytope of projective space is self-dual under primitive duality.
Remark 1.6. The lattice-change phenomenon here is reminiscent of duality for r-Gorenstein polytopes [Reference Batyrev and Nill1] but differs from it because our polytopes are Gorenstein themselves (rather than a multiple of the polytope being Gorenstein).
The inclusion of lattices
![]() $\overline {M} \subset M$
induces an action of the finite group
$\overline {M} \subset M$
induces an action of the finite group
![]() $M/\overline {M}$
on
$M/\overline {M}$
on
![]() $X_Q$
, and
$X_Q$
, and
We can extend this description of Batyrev–Borisov mirror symmetry to a series of mirror pairs, one for each intermediate lattice. The inclusion of lattices
![]() $\overline {M} \subset M$
defines an inclusion
$\overline {M} \subset M$
defines an inclusion
![]() $N \subset \overline {M}^{\vee }$
. We denote
$N \subset \overline {M}^{\vee }$
. We denote
![]() $\overline {N}:=\overline {M}^{\vee }$
. Any intermediate lattice
$\overline {N}:=\overline {M}^{\vee }$
. Any intermediate lattice
![]() $\overline {M} \subset M_1 \subset M$
defines an intermediate dual lattice
$\overline {M} \subset M_1 \subset M$
defines an intermediate dual lattice
Proposition 1.7. Fix a lattice
![]() $\overline {M} \subset M_1 \subset M$
, and let
$\overline {M} \subset M_1 \subset M$
, and let
![]() $N_1$
be the lattice dual to
$N_1$
be the lattice dual to
![]() $M_1$
. Then
$M_1$
. Then
are a Batyrev–Borisov mirror pair.
Proof. Let
![]() $P_1$
denote the image of P in
$P_1$
denote the image of P in
![]() $N_1$
. Then we can describe
$N_1$
. Then we can describe
![]() $X_{P_1}$
as
$X_{P_1}$
as
![]() $X_P/(N_1/N)$
. The dual
$X_P/(N_1/N)$
. The dual
![]() $P_1^{\vee }$
has ambient lattice
$P_1^{\vee }$
has ambient lattice
![]() $M_1$
. The vertices of
$M_1$
. The vertices of
![]() $P_1^{\vee }$
are identified with that of Q under the inclusion
$P_1^{\vee }$
are identified with that of Q under the inclusion
![]() $\overline {M} \subset M_1$
, so
$\overline {M} \subset M_1$
, so
![]() $X_{P_1^{\vee }}$
can be constructed as
$X_{P_1^{\vee }}$
can be constructed as
![]() $X_Q/(M_1/\overline {M})$
.
$X_Q/(M_1/\overline {M})$
.
In the following proposition, we show that primitive duality is a duality, under the assumption that P is vertex spanning.
Proposition 1.8. Let P be a reflexive, vertex-spanning polytope. Let Q be the primitive dual of P. Then the primitive dual of Q is P.
Proof. The dual of the reflexive polytope Q is the image of P under the inclusion of lattice
![]() $N \subset \overline {N}$
. By assumption, P is vertex spanning, and so its vertices generate N. It follows that P is the primitive dual of Q.
$N \subset \overline {N}$
. By assumption, P is vertex spanning, and so its vertices generate N. It follows that P is the primitive dual of Q.
We can be more explicit given the following assumptions on P and
![]() $X_P$
:
$X_P$
:
-
1. There is a Cartier toric divisor
 $D_i$
for some ray i such that
$D_i$
for some ray i such that
 $n D_i$
is linearly equivalent to
$n D_i$
is linearly equivalent to
 $-K_{X_P}$
.
$-K_{X_P}$
. -
2. Both P and
 $P_{D_0}$
are vertex-spanning polytopes.
$P_{D_0}$
are vertex-spanning polytopes.
The two polyhedra
![]() $P_{n D_i}$
and
$P_{n D_i}$
and
![]() $P_{-K_{X_P}}$
are translates of each other. Suppose that
$P_{-K_{X_P}}$
are translates of each other. Suppose that
for some lattice element
![]() $h \in M$
.
$h \in M$
.
Lemma 1.9. The lattice
![]() $\overline {M}$
is generated by h and the generators of
$\overline {M}$
is generated by h and the generators of
![]() $n M$
, and
$n M$
, and
Proof. As noted,
![]() $P^{\vee }=P_{-K_{X_P}}$
. Fix a basis
$P^{\vee }=P_{-K_{X_P}}$
. Fix a basis
![]() $e_1,\dots ,e_d$
of M. The vertices of
$e_1,\dots ,e_d$
of M. The vertices of
![]() $P_{n D_0}$
span the lattice given by the basis
$P_{n D_0}$
span the lattice given by the basis
![]() $n e_j$
. It follows the lattice spanned by the vertices of
$n e_j$
. It follows the lattice spanned by the vertices of
![]() $P^{\vee }$
, that is the lattice
$P^{\vee }$
, that is the lattice
![]() $\overline {M}$
, is the lattice spanned by
$\overline {M}$
, is the lattice spanned by
![]() $n e_1,\dots ,n e_d,h$
. Note that, as
$n e_1,\dots ,n e_d,h$
. Note that, as
![]() $0$
is a vertex of
$0$
is a vertex of
![]() $P_{D_i}$
, h is a vertex of the reflexive polytope
$P_{D_i}$
, h is a vertex of the reflexive polytope
![]() $P^{\vee }$
and hence is a primitive lattice vector. It follows that
$P^{\vee }$
and hence is a primitive lattice vector. It follows that
2 The Gelfand–Cetlin toric degeneration
The goal of this section is to recall the construction of the best-known toric degeneration of the Grassmannian, first studied by Gonciulea–Lakshmibai [Reference Gonciulea and Lakshmibai10]. This is a SAGBI basis degeneration of the Grassmannian inside its Plücker embedding (see [Reference Miller and Sturmfels19] for a good exposition). The polytope giving the degenerate toric variety is a Gelfand–Cetlin polytope, so we will call this toric degeneration the Gelfand–Cetlin toric degeneration. We begin by recalling the details of the construction, including a description of both the polytope and the weight matrix of the toric variety
![]() $X_{P_{n,r}}$
that forms the central fiber. We then describe the primitive dual to the polytope
$X_{P_{n,r}}$
that forms the central fiber. We then describe the primitive dual to the polytope
![]() $P_{n,r}$
and its weight matrix.
$P_{n,r}$
and its weight matrix.
2.1 Ladder diagrams
The polytope
![]() $P_{n,r}$
can be described via a ladder diagram. Fix integers
$P_{n,r}$
can be described via a ladder diagram. Fix integers
![]() $n>r>0$
, and set
$n>r>0$
, and set
![]() $k:=n-r$
. Draw an
$k:=n-r$
. Draw an
![]() $r \times k$
grid of boxes. For example, the grid for
$r \times k$
grid of boxes. For example, the grid for
![]() $n=5$
,
$n=5$
,
![]() $r=2$
is
$r=2$
is

Draw vertices on the diagram as follows: at all internal crossing points and at the bottom-left and top-right corner. Continuing this example, we obtain

We consider paths in this diagram between vertices, where travel is always up and to the right. This describes a quiver: Vertices are given by the vertices in the ladder diagram, and there is an arrow from vertex a to b for every path in the ladder diagram which does not pass through any other vertex. In the example, the quiver is

Definition 2.1. We call this quiver the ladder quiver
![]() $\operatorname {{\mathrm {LQ}}}$
, or
$\operatorname {{\mathrm {LQ}}}$
, or
![]() $\operatorname {{\mathrm {LQ}}}(n,r)$
if n and r are not clear from context. The set of vertices of the ladder quiver is denoted by
$\operatorname {{\mathrm {LQ}}}(n,r)$
if n and r are not clear from context. The set of vertices of the ladder quiver is denoted by
![]() $\operatorname {{\mathrm {LQ}}}_0$
and the set of arrows by
$\operatorname {{\mathrm {LQ}}}_0$
and the set of arrows by
![]() $\operatorname {{\mathrm {LQ}}}_1$
. We denote the source and target maps by s,
$\operatorname {{\mathrm {LQ}}}_1$
. We denote the source and target maps by s,
![]() $t:\operatorname {{\mathrm {LQ}}}_1 \to \operatorname {{\mathrm {LQ}}}_0$
. Let
$t:\operatorname {{\mathrm {LQ}}}_1 \to \operatorname {{\mathrm {LQ}}}_0$
. Let
![]() $0 \in \operatorname {{\mathrm {LQ}}}_0$
be the source vertex. Let
$0 \in \operatorname {{\mathrm {LQ}}}_0$
be the source vertex. Let
![]() $\overline {\operatorname {{\mathrm {LQ}}}}_0$
denote the set of vertices with the source vertex omitted.
$\overline {\operatorname {{\mathrm {LQ}}}}_0$
denote the set of vertices with the source vertex omitted.
Remark 2.2. We henceforth draw the ladder quiver as a ladder diagram, leaving the directions of the arrows implicit.
A quiver moduli space is defined by assigning a vector space to each vertex of a quiver and choosing a stability condition [Reference King15]. If we assign a one-dimensional vector space to each vertex of the ladder quiver and choose a Fano stability condition, then we obtain a quiver moduli space that coincides with
![]() $X_{P_{n,r}}$
: See [Reference Kalashnikov14] for details.
$X_{P_{n,r}}$
: See [Reference Kalashnikov14] for details.
The weight matrix of
![]() $X_{P_{n,r}}$
is given by the adjacency matrix of the ladder quiver. More precisely, let
$X_{P_{n,r}}$
is given by the adjacency matrix of the ladder quiver. More precisely, let
![]() $\mathbb {Z}^{\overline {\operatorname {{\mathrm {LQ}}}}_0}$
be the lattice with basis
$\mathbb {Z}^{\overline {\operatorname {{\mathrm {LQ}}}}_0}$
be the lattice with basis
![]() $e_v, v \in \overline {\operatorname {{\mathrm {LQ}}}}_0$
. For the source vertex
$e_v, v \in \overline {\operatorname {{\mathrm {LQ}}}}_0$
. For the source vertex
![]() $0 \in \operatorname {{\mathrm {LQ}}}_0$
, set
$0 \in \operatorname {{\mathrm {LQ}}}_0$
, set
![]() $e_0=0$
. Then the weights are given by
$e_0=0$
. Then the weights are given by
![]() $d_a:=-e_{s(a)}+e_{t(a)}$
.
$d_a:=-e_{s(a)}+e_{t(a)}$
.
It is often more convenient to write the weights in a different basis. We identify a basis element
![]() $f_v$
for each
$f_v$
for each
![]() $v \in \overline {LQ}_0$
, as follows:
$v \in \overline {LQ}_0$
, as follows:
-
1. If all arrows with
 $t(a)=v$
have
$t(a)=v$
have
 $s(a)=0$
, then we set
$s(a)=0$
, then we set
 $f_v:=d_a=e_v$
.
$f_v:=d_a=e_v$
. -
2. If there is a unique arrow such that both
 $t(a)=v$
and
$t(a)=v$
and
 $s(a) \neq 0$
, then we set
$s(a) \neq 0$
, then we set
 $f_v:=d_a$
.
$f_v:=d_a$
. -
3. Otherwise, v is the top-right corner of a square of vertices. Label the other vertices of the square as shown:

then set
 $$\begin{align*}f_v:=e_{v}-e_{v_1}-e_{v_2}+e_{v_0}. \end{align*}$$
$$\begin{align*}f_v:=e_{v}-e_{v_1}-e_{v_2}+e_{v_0}. \end{align*}$$
That is,
 $f_v$
is a sum
$f_v$
is a sum
 $\sum d_a$
where a runs through the arrows drawn in the diagram:
$\sum d_a$
where a runs through the arrows drawn in the diagram:
In the basis
![]() $f_v$
,
$f_v$
,
![]() $v \in \overline {LQ}_0$
, the weight matrix
$v \in \overline {LQ}_0$
, the weight matrix
has rows indexed by
![]() $v \in \overline {\operatorname {{\mathrm {LQ}}}}_0$
, columns indexed by
$v \in \overline {\operatorname {{\mathrm {LQ}}}}_0$
, columns indexed by
![]() $a \in \operatorname {{\mathrm {LQ}}}_1$
, and all entries are either
$a \in \operatorname {{\mathrm {LQ}}}_1$
, and all entries are either
![]() $1$
or
$1$
or
![]() $0$
. There are precisely n positive entries in each row. It is easy to identify visually the set
$0$
. There are precisely n positive entries in each row. It is easy to identify visually the set
for each v. We describe it by way of example.
Example 2.3. Let
![]() $n=7$
and
$n=7$
and
![]() $r=3$
. For each nonsource vertex v, labeled in red, the arrows satisfying
$r=3$
. For each nonsource vertex v, labeled in red, the arrows satisfying
![]() $b_{v a}=1$
are the n arrows fully contained in the red part of the ladder quiver.
$b_{v a}=1$
are the n arrows fully contained in the red part of the ladder quiver.


As one can see from the example, for a nonsource vertex v,
![]() $b_{v a}=1$
if a is an arrow that either
$b_{v a}=1$
if a is an arrow that either
-
○ has a horizontal step above and in the same column as the horizontal arrow with target v or
-
○ has a vertical step to the right and in the same row as the vertical arrow with target v.
In particular, every path from the bottom-left to top-right corner contains exactly one of the arrows in
for each v.
A great deal of the geometry of the special fiber
![]() $X_{P_{n,r}}$
can be read off the ladder quiver. For example, collections of arrows give divisors. The toric variety
$X_{P_{n,r}}$
can be read off the ladder quiver. For example, collections of arrows give divisors. The toric variety
![]() $X_{P_{n,r}}$
has Picard rank 1, and the Picard lattice is generated by a divisor corresponding to a path from the bottom-left vertex to the top right; each such path is linearly equivalent to the ample generator for the Picard lattice. This generator is the ample line bundle that gives the embedding of
$X_{P_{n,r}}$
has Picard rank 1, and the Picard lattice is generated by a divisor corresponding to a path from the bottom-left vertex to the top right; each such path is linearly equivalent to the ample generator for the Picard lattice. This generator is the ample line bundle that gives the embedding of
![]() $X_{P_{n,r}}$
into
$X_{P_{n,r}}$
into
![]() $\mathbb {P}^{\binom {n}{r}-1}$
, where it is the special fiber of the Gelfand–Cetlin degeneration. As such, we label it
$\mathbb {P}^{\binom {n}{r}-1}$
, where it is the special fiber of the Gelfand–Cetlin degeneration. As such, we label it
![]() $\mathcal {O}(1)$
. The space of sections of
$\mathcal {O}(1)$
. The space of sections of
![]() $\mathcal {O}(1)$
has dimension
$\mathcal {O}(1)$
has dimension
![]() $\binom {n}{r}$
and basis indexed by paths from the bottom-left vertex to the top right. Fixing such a path p, we can consider the area above p: This gives a partition
$\binom {n}{r}$
and basis indexed by paths from the bottom-left vertex to the top right. Fixing such a path p, we can consider the area above p: This gives a partition
![]() $\lambda $
which fits into an
$\lambda $
which fits into an
![]() $r \times k$
box. We label the corresponding section of
$r \times k$
box. We label the corresponding section of
![]() $\mathcal {O}(1)$
by
$\mathcal {O}(1)$
by
![]() $s_{\lambda }$
. The Cox ring is a polynomial ring
$s_{\lambda }$
. The Cox ring is a polynomial ring
![]() ${\mathbb {C}}[y_a: a \in \operatorname {{\mathrm {LQ}}}_1]$
, and
${\mathbb {C}}[y_a: a \in \operatorname {{\mathrm {LQ}}}_1]$
, and
![]() $s_{\lambda } = \prod _{a \in p} y_a$
.
$s_{\lambda } = \prod _{a \in p} y_a$
.
Partitions fitting into an
![]() $r \times k$
box also index Plücker coordinates. Given a partition
$r \times k$
box also index Plücker coordinates. Given a partition
![]() $\lambda $
, there are n horizontal and vertical steps in the corresponding path p, and the location of the vertical steps gives a size-r subset of
$\lambda $
, there are n horizontal and vertical steps in the corresponding path p, and the location of the vertical steps gives a size-r subset of
![]() $\{1,\dots ,n\}$
.
$\{1,\dots ,n\}$
.
Definition 2.4. We denote by
![]() ${\mathcal {P}(n,r)}$
the set of partitions
${\mathcal {P}(n,r)}$
the set of partitions
![]() $\lambda $
that fit into an
$\lambda $
that fit into an
![]() $r \times k$
box. If
$r \times k$
box. If
![]() $\lambda \in {\mathcal {P}(n,r)}$
, we define
$\lambda \in {\mathcal {P}(n,r)}$
, we define
![]() $I_{\lambda }$
to be the corresponding size-r subset of
$I_{\lambda }$
to be the corresponding size-r subset of
![]() $\{1,\dots ,n\}$
.
$\{1,\dots ,n\}$
.
Example 2.5. The ladder diagram for
![]() $Gr(7,3)$
is below. The path in blue describes the partition
$Gr(7,3)$
is below. The path in blue describes the partition
![]() $(2,1)$
. This indexes the Plücker coordinate
$(2,1)$
. This indexes the Plücker coordinate
![]() $p_{\{1,3,5\}}$
.
$p_{\{1,3,5\}}$
.

2.2 The polytope
 $P_{n,r}$
and its primitive dual
$P_{n,r}$
and its primitive dual
To describe the Gelfand–Cetlin toric degeneration via a polytope, we draw another quiver dual to the ladder quiver (this is the quiver that gives the head-over-tails mirror [Reference Eguchi, Hori and Xiong9]). There is a vertex for the dual quiver in each square of the ladder diagram, as well as two external vertices above and to the right of the ladder diagram. Arrows move down and to the left, so we obtain:

Each arrow in the ladder quiver is crossed by precisely one arrow in the dual quiver.
Notice that there are
![]() $k r$
interior vertices. Let M be an
$k r$
interior vertices. Let M be an
![]() $k r$
-dimensional lattice, where we index the basis
$k r$
-dimensional lattice, where we index the basis
![]() $e^{\prime }_v$
by interior vertices v in the dual quiver. Set
$e^{\prime }_v$
by interior vertices v in the dual quiver. Set
![]() $e^{\prime }_v=0$
for external vertices v.
$e^{\prime }_v=0$
for external vertices v.
Definition 2.6. The polytope
![]() $P_{n,r}$
has a vertex for each arrow in the dual quiver. The vertex for arrow a is
$P_{n,r}$
has a vertex for each arrow in the dual quiver. The vertex for arrow a is
![]() $w_{a}:=-e^{\prime }_{s(a)}+e^{\prime }_{t(a)} \in M$
.
$w_{a}:=-e^{\prime }_{s(a)}+e^{\prime }_{t(a)} \in M$
.
Sometimes, instead of the basis
![]() $e^{\prime }_v$
it is convenient to use another basis, given by arrows. For each internal vertex v in the dual quiver, we assign an arrow
$e^{\prime }_v$
it is convenient to use another basis, given by arrows. For each internal vertex v in the dual quiver, we assign an arrow
![]() $a_v$
. If there is a horizontal arrow out of vertex v, then this is
$a_v$
. If there is a horizontal arrow out of vertex v, then this is
![]() $a_v$
; otherwise,
$a_v$
; otherwise,
![]() $a_v$
is the vertical arrow out of v. Then we set
$a_v$
is the vertical arrow out of v. Then we set
![]() $b_v:=w_{a_v}$
. In the diagram below, we highlight the arrows
$b_v:=w_{a_v}$
. In the diagram below, we highlight the arrows
![]() $a_v$
in red for
$a_v$
in red for
![]() $n=7, r=3$
.
$n=7, r=3$
.

Let N be the lattice dual to M, with dual bases
![]() ${e'}_v^{\vee }$
and
${e'}_v^{\vee }$
and
![]() $b_v^{\vee }$
. We now construct the primitive dual of
$b_v^{\vee }$
. We now construct the primitive dual of
![]() $P_{n,r}$
, which we call
$P_{n,r}$
, which we call
![]() $Q_{n,r}$
. By definition, this is the pullback of the anticanonical polytope of
$Q_{n,r}$
. By definition, this is the pullback of the anticanonical polytope of
![]() $X_{P_{n,r}}$
to the lattice spanned by its vertices. We construct it in three stages:
$X_{P_{n,r}}$
to the lattice spanned by its vertices. We construct it in three stages:
-
1. Construct the polytope for the divisor given by the path corresponding to the empty partition.
-
2. Compare the n-th dilate of this polytope with anticanonical polytope of
 $X_{P_{n,r}}$
.
$X_{P_{n,r}}$
. -
3. Compute the sublattice generated by the vertices of the polytope.
Let
![]() $D_{\varnothing }$
denote the divisor corresponding to the empty partition. The path corresponding to the empty set consists of exactly one arrow, which we denote
$D_{\varnothing }$
denote the divisor corresponding to the empty partition. The path corresponding to the empty set consists of exactly one arrow, which we denote
![]() $a_{\varnothing } $
. Set
$a_{\varnothing } $
. Set
Lemma 2.7. Let a be an arrow in the dual quiver that is not
![]() $a_{\varnothing } $
and
$a_{\varnothing } $
and
![]() $\lambda $
a path that does not correspond to
$\lambda $
a path that does not correspond to
![]() $\varnothing $
. Then
$\varnothing $
. Then
if
![]() $\lambda $
crosses a and is
$\lambda $
crosses a and is
![]() $0$
otherwise.
$0$
otherwise.
Proof. To compute, we consider both vectors written in the
![]() $b_{v}$
or
$b_{v}$
or
![]() $b_v^{\vee }$
basis. The statement is obvious if
$b_v^{\vee }$
basis. The statement is obvious if
![]() $a=a_v$
for some v. Otherwise, we can assume that a is a vertical arrow with both source and target internal vertices. The vector
$a=a_v$
for some v. Otherwise, we can assume that a is a vertical arrow with both source and target internal vertices. The vector
![]() $w_a$
is expanded in the
$w_a$
is expanded in the
![]() $b_v$
by following the path starting at
$b_v$
by following the path starting at
![]() $s(a)$
, going all the way to the right, then down, and then going in reverse back to
$s(a)$
, going all the way to the right, then down, and then going in reverse back to
![]() $t(a)$
. Then
$t(a)$
. Then
![]() $w_a$
is the sum of these
$w_a$
is the sum of these
![]() $b_v$
, where
$b_v$
, where
![]() $b_v$
has coefficient
$b_v$
has coefficient
![]() $\pm 1$
, depending on whether it followed in the positive direction or in reverse. Note that the number of arrows followed in the positive direction is one more than the number of arrows in the reverse direction.
$\pm 1$
, depending on whether it followed in the positive direction or in reverse. Note that the number of arrows followed in the positive direction is one more than the number of arrows in the reverse direction.
Suppose
![]() $\lambda $
crosses a. After crossing a, it must cross exactly one of the arrows going in the positive direction, so
$\lambda $
crosses a. After crossing a, it must cross exactly one of the arrows going in the positive direction, so
![]() $\langle m_{\lambda },w_a\rangle =1$
. If
$\langle m_{\lambda },w_a\rangle =1$
. If
![]() $\lambda $
does not cross a, it either avoids the arrows used in the expansion of
$\lambda $
does not cross a, it either avoids the arrows used in the expansion of
![]() $w_a$
entirely, or it crosses one arrow in the reverse direction and one arrow in the positive, so
$w_a$
entirely, or it crosses one arrow in the reverse direction and one arrow in the positive, so
For an illustration, consider the following example:

Corollary 2.8. The polytope
![]() $P_{D_{\varnothing }}$
corresponding to the divisor
$P_{D_{\varnothing }}$
corresponding to the divisor
![]() $D_{\varnothing } $
is the convex hull of the points
$D_{\varnothing } $
is the convex hull of the points
 $$\begin{align*}\left\{m_{\lambda}:=\sum_{\lambda \text{ crosses } a_v} b^{\vee}_v \Bigg| \lambda \in {\mathcal{P}(n,r)} \right\}. \end{align*}$$
$$\begin{align*}\left\{m_{\lambda}:=\sum_{\lambda \text{ crosses } a_v} b^{\vee}_v \Bigg| \lambda \in {\mathcal{P}(n,r)} \right\}. \end{align*}$$
Proof. One easy way to see the claim is to check that points in this polytope homogenize to sections of
![]() $D_{\varnothing }$
. This is the case if
$D_{\varnothing }$
. This is the case if
![]() $m_{\varnothing }$
is the origin and for all other partitions
$m_{\varnothing }$
is the origin and for all other partitions
![]() $\lambda $
:
$\lambda $
:
-
○
 $\langle m_{\lambda }, w_{a_{\varnothing } } \rangle = -1$
,
$\langle m_{\lambda }, w_{a_{\varnothing } } \rangle = -1$
, -
○
 $\langle m_{\lambda }, w_a \rangle =1$
if a is in the path
$\langle m_{\lambda }, w_a \rangle =1$
if a is in the path
 $\lambda $
and
$\lambda $
and
 $\langle m_{\lambda }, w_a \rangle =0$
otherwise.
$\langle m_{\lambda }, w_a \rangle =0$
otherwise.
The first condition is easy to check visually, and the second is precisely Lemma 2.7.
To compute
![]() $P_{n,r}^{\vee }$
, one must dilate the polyhedron
$P_{n,r}^{\vee }$
, one must dilate the polyhedron
![]() $P_{D_{\varnothing } }$
by a factor of n and then perform a linear shift. That is,
$P_{D_{\varnothing } }$
by a factor of n and then perform a linear shift. That is,
where
![]() $h=\sum _{v} b_v$
. This can be seen by comparing the homogenization procedure of
$h=\sum _{v} b_v$
. This can be seen by comparing the homogenization procedure of
![]() $P_{n D_{\varnothing } }$
and
$P_{n D_{\varnothing } }$
and
![]() $P_{-\sum D_a}=P_{n,r}^{\vee }$
. It follows that the vertices of
$P_{-\sum D_a}=P_{n,r}^{\vee }$
. It follows that the vertices of
![]() $P_{n,r}^{\vee }$
are
$P_{n,r}^{\vee }$
are
Finally, we note that the lattice
![]() $\overline {M}$
generated by
$\overline {M}$
generated by
![]() $h, \{n b_v: v \text { an interior vertex}\}$
is the lattice generated by the vertices of
$h, \{n b_v: v \text { an interior vertex}\}$
is the lattice generated by the vertices of
![]() $P_{n,r}^{\vee }$
. The preimage of
$P_{n,r}^{\vee }$
. The preimage of
![]() $P_{n,r}^{\vee }$
under the inclusion of lattice
$P_{n,r}^{\vee }$
under the inclusion of lattice
![]() $\overline {M} \subset M$
is by definition the primitive dual
$\overline {M} \subset M$
is by definition the primitive dual
![]() $Q_{n,r}$
. This is a Fano reflexive polytope with
$Q_{n,r}$
. This is a Fano reflexive polytope with
![]() $\binom {n}{r}$
vertices, labeled by partitions
$\binom {n}{r}$
vertices, labeled by partitions
![]() $\lambda \in {\mathcal {P}(n,r)}.$
We denote the vertices of
$\lambda \in {\mathcal {P}(n,r)}.$
We denote the vertices of
![]() $Q_{n,r}$
as
$Q_{n,r}$
as
![]() $v_{\lambda }$
,
$v_{\lambda }$
,
![]() $\lambda \in {\mathcal {P}(n,r)}$
.
$\lambda \in {\mathcal {P}(n,r)}$
.
2.3 Weights of
 $X_{Q_{n,r}}$
$X_{Q_{n,r}}$
As
![]() $Q_{n,r}$
is a Fano reflexive polytope, we can consider the Fano toric variety
$Q_{n,r}$
is a Fano reflexive polytope, we can consider the Fano toric variety
![]() $X_{Q_n,r}$
. We will describe a spanning set of the kernel of the ray sequence (a basis for the kernel would give the rows of a weight matrix). There is a relation for each m-covering of the ladder quiver
$X_{Q_n,r}$
. We will describe a spanning set of the kernel of the ray sequence (a basis for the kernel would give the rows of a weight matrix). There is a relation for each m-covering of the ladder quiver
![]() $\operatorname {{\mathrm {LQ}}}$
.
$\operatorname {{\mathrm {LQ}}}$
.
Definition 2.9. An m-covering of the ladder quiver
![]() $\operatorname {{\mathrm {LQ}}}$
is a collection of partitions such that the collection of associated paths in the ladder quiver contains each arrow precisely m times.
$\operatorname {{\mathrm {LQ}}}$
is a collection of partitions such that the collection of associated paths in the ladder quiver contains each arrow precisely m times.
The
![]() $1$
-coverings are given by crossing diagrams.
$1$
-coverings are given by crossing diagrams.
Definition 2.10. A crossing diagram of
![]() $\operatorname {{\mathrm {LQ}}}_{n,r}$
is an assignment of X or O to each internal vertex of
$\operatorname {{\mathrm {LQ}}}_{n,r}$
is an assignment of X or O to each internal vertex of
![]() $\operatorname {{\mathrm {LQ}}}_{n,r}$
.
$\operatorname {{\mathrm {LQ}}}_{n,r}$
.
For example, the following is a crossing diagram for
![]() $\operatorname {{\mathrm {LQ}}}_{5,2}$
.
$\operatorname {{\mathrm {LQ}}}_{5,2}$
.

A crossing diagram defines a set of n partitions in
![]() ${\mathcal {P}(n,r)}$
. Each partition corresponds to a path in the ladder quiver. A path
${\mathcal {P}(n,r)}$
. Each partition corresponds to a path in the ladder quiver. A path
![]() $\lambda $
is a path for a given crossing diagram if
$\lambda $
is a path for a given crossing diagram if
-
○ For every vertex labeled X, if the path
 $\lambda $
contains this vertex, it goes straight through this vertex.
$\lambda $
contains this vertex, it goes straight through this vertex. -
○ For every vertex labeled O, if the path
 $\lambda $
contains this vertex, it makes a
$\lambda $
contains this vertex, it makes a
 $90^{\circ }$
turn at this vertex.
$90^{\circ }$
turn at this vertex.
If we continue the same example as above, the paths are
. Notice that the empty partition and the maximal partition
![]() $(k^r)$
are paths for every crossing diagram. Together, the paths of a fixed crossing diagram cover every arrow in the ladder quiver precisely once, so they are a
$(k^r)$
are paths for every crossing diagram. Together, the paths of a fixed crossing diagram cover every arrow in the ladder quiver precisely once, so they are a
![]() $1$
-covering.
$1$
-covering.
Proposition 2.11. Let
![]() $\{\lambda _i\}$
be the
$\{\lambda _i\}$
be the
![]() $m n$
paths of an m-covering of a ladder quiver. Then
$m n$
paths of an m-covering of a ladder quiver. Then
![]() $\sum _{i=1}^{mn} v_{\lambda _i}=0.$
These relations span all relations amongst the
$\sum _{i=1}^{mn} v_{\lambda _i}=0.$
These relations span all relations amongst the
![]() $v_{\lambda }$
.
$v_{\lambda }$
.
Proof. To show the first part of the proposition, note that, though the
![]() $v_{\lambda }$
are vectors in the sublattice
$v_{\lambda }$
are vectors in the sublattice
![]() $\overline {M}$
spanned by the vertices of
$\overline {M}$
spanned by the vertices of
![]() $Q_{n,r}$
, it is equivalent to show that
$Q_{n,r}$
, it is equivalent to show that
 $$\begin{align*}\sum_{i=1}^{mn} i(v_{\lambda_i})=0, \qquad \text{that is,} \qquad \sum_{i=1}^{mn} (n m_{\lambda_i}-h) = 0. \end{align*}$$
$$\begin{align*}\sum_{i=1}^{mn} i(v_{\lambda_i})=0, \qquad \text{that is,} \qquad \sum_{i=1}^{mn} (n m_{\lambda_i}-h) = 0. \end{align*}$$
Here, i is the inclusion
![]() $i:\overline {M} \to M$
.
$i:\overline {M} \to M$
.
Recall that
![]() $m_{\lambda }:=\sum _{\lambda \text { crosses } a_v} b^{\vee }_v$
. Since the collection of paths
$m_{\lambda }:=\sum _{\lambda \text { crosses } a_v} b^{\vee }_v$
. Since the collection of paths
![]() $\{\lambda _i\}$
together cover each arrow in
$\{\lambda _i\}$
together cover each arrow in
![]() $\operatorname {{\mathrm {LQ}}}$
exactly m times, it follows that
$\operatorname {{\mathrm {LQ}}}$
exactly m times, it follows that
 $$\begin{align*}\sum_{i=1}^{mn} m_{\lambda_i}=\sum_{v} b_v^{\vee}= m h, \end{align*}$$
$$\begin{align*}\sum_{i=1}^{mn} m_{\lambda_i}=\sum_{v} b_v^{\vee}= m h, \end{align*}$$
which is equivalent to the desired equality.
For the second part of the proposition, suppose there is some collection
![]() $\{\mu _1,\dots ,\mu _k\}$
and coefficients
$\{\mu _1,\dots ,\mu _k\}$
and coefficients
![]() $a_i$
satisfying
$a_i$
satisfying
 $$\begin{align*}\sum_{i=1}^k a_i v_{\mu_i}=0. \end{align*}$$
$$\begin{align*}\sum_{i=1}^k a_i v_{\mu_i}=0. \end{align*}$$
Note that we can assume, by adding multiples of the relations obtained from the crossing diagrams if necessary, that all the
![]() $a_i$
are nonnegative. In fact, if we allow partitions to appear multiple times, we can assume that the
$a_i$
are nonnegative. In fact, if we allow partitions to appear multiple times, we can assume that the
![]() $a_i=1$
.
$a_i=1$
.
As above, we convert this to an equality in N, where we see that
 $$\begin{align*}\sum_{i=1}^k (n m_{\mu_i}-h)=0. \end{align*}$$
$$\begin{align*}\sum_{i=1}^k (n m_{\mu_i}-h)=0. \end{align*}$$
It follows that k is a multiple of n and
 $$\begin{align*}\sum_{i=1}^k m_{\mu_i}=\frac{k}{n} h. \end{align*}$$
$$\begin{align*}\sum_{i=1}^k m_{\mu_i}=\frac{k}{n} h. \end{align*}$$
If we reinterpret this as a statement about ladder diagrams, it says that, for each basis arrow
![]() $a_v$
in the dual quiver, precisely
$a_v$
in the dual quiver, precisely
![]() $k/n$
of the paths
$k/n$
of the paths
![]() $\mu _i$
cross
$\mu _i$
cross
![]() $a_v$
.
$a_v$
.
In fact, this is enough to show that precisely
![]() $k/n$
of the paths
$k/n$
of the paths
![]() $\mu _i$
cross any arrow in the dual quiver. To see this, first consider a nonbasis arrow a,
$\mu _i$
cross any arrow in the dual quiver. To see this, first consider a nonbasis arrow a,
![]() $a \neq a_{\varnothing } $
. It is a vertical arrow with internal source and target (in the dual quiver). There is a rectangle of arrows in the dual diagram, with vertical arrow a on the left side, and all other arrows (on the boundary) basis arrows. For example, this is such a rectangle (where a is the green arrow and the red arrows are—as before—the
$a \neq a_{\varnothing } $
. It is a vertical arrow with internal source and target (in the dual quiver). There is a rectangle of arrows in the dual diagram, with vertical arrow a on the left side, and all other arrows (on the boundary) basis arrows. For example, this is such a rectangle (where a is the green arrow and the red arrows are—as before—the
![]() $a_v$
):
$a_v$
):

In general, there will be zero or more black vertical arrows in between the green vertical arrow and the red vertical arrow. Each of the red arrows is crossed
![]() $k/n$
times, and suppose a is crossed s times. If the width of the rectangle is t arrows, this means there are
$k/n$
times, and suppose a is crossed s times. If the width of the rectangle is t arrows, this means there are
![]() $s+t k/n$
paths
$s+t k/n$
paths
![]() $\mu _i$
entering the rectangle, and
$\mu _i$
entering the rectangle, and
![]() $(t+1)k/n$
paths exiting the rectangle. So we can conclude that
$(t+1)k/n$
paths exiting the rectangle. So we can conclude that
![]() $s=k/n$
. Therefore, the collection of arrows
$s=k/n$
. Therefore, the collection of arrows
![]() $\mu _i$
cover the ladder diagram, omitting the arrow dual to
$\mu _i$
cover the ladder diagram, omitting the arrow dual to
![]() $a_{\varnothing } $
, exactly
$a_{\varnothing } $
, exactly
![]() $k/n$
times.
$k/n$
times.
Finally, now suppose that
![]() $a_{\varnothing } $
is crossed r times by the paths— that is, r of the
$a_{\varnothing } $
is crossed r times by the paths— that is, r of the
![]() $\mu _i$
are the path corresponding to the empty set. The remaining arrows do not cross
$\mu _i$
are the path corresponding to the empty set. The remaining arrows do not cross
![]() $a_{\varnothing } $
, but they cover the rest of the diagram
$a_{\varnothing } $
, but they cover the rest of the diagram
![]() $k/n$
times so that means that there are
$k/n$
times so that means that there are
![]() $(n-1)k/n$
of them. Since
$(n-1)k/n$
of them. Since
![]() $r+(n-1)k/n=k$
, we conclude that
$r+(n-1)k/n=k$
, we conclude that
![]() $r=k/n$
as required. So the set
$r=k/n$
as required. So the set
![]() $\{\mu _i\}$
is a
$\{\mu _i\}$
is a
![]() $k/n$
-covering.
$k/n$
-covering.
This proposition characterizes a (redundant form of) the weight matrix.
Remark 2.12. We expect that the relations from
![]() $1$
-coverings span all of the relations but did not manage to prove this and do not require it in what follows.
$1$
-coverings span all of the relations but did not manage to prove this and do not require it in what follows.
2.4 Grassmannian twins
One of the more interesting examples of Batyrev–Borisov mirror pairs obtained from lattice inclusions is the quintic twin [Reference Doran and Morgan8]. This is a hypersurface in a quotient of projective space whose Picard–Fuchs equations are identical to that of the quintic. The quotient is obtained by taking the action on
![]() $\mathbb {P}^4$
of the group
$\mathbb {P}^4$
of the group
![]() $\mu _5$
of fifth roots of unity given by
$\mu _5$
of fifth roots of unity given by
Let
![]() $\tilde {P}$
denote the polytope of the quotient, a lattice polytope in
$\tilde {P}$
denote the polytope of the quotient, a lattice polytope in
![]() $\tilde {M}$
, and P the polytope of projective space, a lattice polytope in M. Then the group action corresponds to a lattice inclusion
$\tilde {M}$
, and P the polytope of projective space, a lattice polytope in M. Then the group action corresponds to a lattice inclusion
![]() $i:M \subset \tilde {M}$
. The fact that the Picard–Fuchs equations are identical follows from the fact that
$i:M \subset \tilde {M}$
. The fact that the Picard–Fuchs equations are identical follows from the fact that
![]() $i^{-1}(\tilde {P})$
is isomorphic to P.
$i^{-1}(\tilde {P})$
is isomorphic to P.
The perspective on mirror symmetry for high-index Fano varieties described in this paper also suggests that the quintic twin can be generalized to Grassmannians, as in the following example.
Example 2.13. Consider the action of the group
![]() $\mu _5$
on
$\mu _5$
on
![]() $\operatorname {{\mathrm {Mat}}}(2 \times 5)$
given by multiplication on the right by diagonal matrices with entries
$\operatorname {{\mathrm {Mat}}}(2 \times 5)$
given by multiplication on the right by diagonal matrices with entries
![]() $(1,\zeta ,\dots , \zeta ^4)$
. This extends to an action on the ambient space of the Plücker embedding, and hence also on the Gelfand–Cetlin degeneration. Let
$(1,\zeta ,\dots , \zeta ^4)$
. This extends to an action on the ambient space of the Plücker embedding, and hence also on the Gelfand–Cetlin degeneration. Let
![]() $\tilde {P}_{2,5}$
denote the lattice polytope corresponding to the quotient by K of the Gelfand–Cetlin degeneration. Denote the ambient lattice of
$\tilde {P}_{2,5}$
denote the lattice polytope corresponding to the quotient by K of the Gelfand–Cetlin degeneration. Denote the ambient lattice of
![]() $P_{2,5}$
as M and the ambient lattice of
$P_{2,5}$
as M and the ambient lattice of
![]() $\tilde {P}_{2,5}$
as
$\tilde {P}_{2,5}$
as
![]() $\tilde {M}$
. As for projective space, there is an inclusion of lattices
$\tilde {M}$
. As for projective space, there is an inclusion of lattices
![]() $i:M \subset \tilde {M}$
and
$i:M \subset \tilde {M}$
and
![]() $i^{-1}(\tilde {P}_{2,5}) \cong P_{2,5}$
. The toric variety associated to
$i^{-1}(\tilde {P}_{2,5}) \cong P_{2,5}$
. The toric variety associated to
![]() $\tilde {P}_{2,5}$
is a toric degeneration of
$\tilde {P}_{2,5}$
is a toric degeneration of
![]() $\operatorname {{\mathrm {Gr}}}(2,5)/K$
.
$\operatorname {{\mathrm {Gr}}}(2,5)/K$
.
Conjectures that form part of the Corti–Golyshev Fanosearch program [Reference Coates, Corti, Galkin, Golyshev and Kasprzyk5] would imply that the quantum periods of
![]() $\operatorname {{\mathrm {Gr}}}(2,5)$
and
$\operatorname {{\mathrm {Gr}}}(2,5)$
and
![]() $\operatorname {{\mathrm {Gr}}}(2,5)/K$
—which are generating functions for the genus-zero Gromov–Witten invariants of the two spaces—can be computed as classical periods of Laurent polynomials f and
$\operatorname {{\mathrm {Gr}}}(2,5)/K$
—which are generating functions for the genus-zero Gromov–Witten invariants of the two spaces—can be computed as classical periods of Laurent polynomials f and
![]() $\tilde {f}$
with Newton polytopes
$\tilde {f}$
with Newton polytopes
![]() $P_{2,5}$
and
$P_{2,5}$
and
![]() $\tilde {P}_{2,5}$
, respectively. (The statement about
$\tilde {P}_{2,5}$
, respectively. (The statement about
![]() $\operatorname {{\mathrm {Gr}}}(2,5)$
has been proven by Marsh–Rietsch [Reference Marsh and Rietsch18].) Since f and
$\operatorname {{\mathrm {Gr}}}(2,5)$
has been proven by Marsh–Rietsch [Reference Marsh and Rietsch18].) Since f and
![]() $\tilde {f}$
differ only by changing the lattice of exponents, they have the same classical period. Thus, we expect that the quantum periods of
$\tilde {f}$
differ only by changing the lattice of exponents, they have the same classical period. Thus, we expect that the quantum periods of
![]() $\operatorname {{\mathrm {Gr}}}(2,5)$
and
$\operatorname {{\mathrm {Gr}}}(2,5)$
and
![]() $\operatorname {{\mathrm {Gr}}}(2,5)/K$
should coincide. In other words, their anticanonical Calabi–Yau sections exhibit a ‘twin phenomenon’.
$\operatorname {{\mathrm {Gr}}}(2,5)/K$
should coincide. In other words, their anticanonical Calabi–Yau sections exhibit a ‘twin phenomenon’.
3 The Gelfand–Cetlin degeneration and variation of GIT
The Grassmannian degenerates to the toric variety
![]() $X_{P_{n,r}}$
, to which Batyrev–Borisov duality can be applied. The primitive dual
$X_{P_{n,r}}$
, to which Batyrev–Borisov duality can be applied. The primitive dual
![]() $Q_{n,r}$
of
$Q_{n,r}$
of
![]() $P_{n,r}$
has been defined and constructed in the previous section. The Batyrev–Borisov mirror of
$P_{n,r}$
has been defined and constructed in the previous section. The Batyrev–Borisov mirror of
![]() $X_{P_{n,r}}$
is
$X_{P_{n,r}}$
is
![]() $X_{Q_{n,r}}/G$
, and the Batyrev–Borisov mirror of
$X_{Q_{n,r}}/G$
, and the Batyrev–Borisov mirror of
![]() $X_{Q_{n,r}}$
is
$X_{Q_{n,r}}$
is
![]() $X_{P_{n,r}}/G$
, where
$X_{P_{n,r}}/G$
, where
![]() $G \cong (\mathbb {Z}/n \mathbb {Z})^{r(n-r)-1}.$
The action of the group is determined by the lattice inclusions that define the primitive dual. In this section, we will explore the relationship between
$G \cong (\mathbb {Z}/n \mathbb {Z})^{r(n-r)-1}.$
The action of the group is determined by the lattice inclusions that define the primitive dual. In this section, we will explore the relationship between
![]() $P_{n,r}$
and
$P_{n,r}$
and
![]() $Q_{n,r}$
in more detail. We will see that there is a weak Fano toric variety
$Q_{n,r}$
in more detail. We will see that there is a weak Fano toric variety
![]() $Y_{n,r}$
that fits into the diagrams
$Y_{n,r}$
that fits into the diagrams

Remark 3.1. The VGITs here are K-equivalences, and so
![]() $X_{P_{n,r}}$
and
$X_{P_{n,r}}$
and
![]() $X_{Q_{n,r}}$
are related by (a natural generalization of) a geometric transition. In the Calabi–Yau threefold case, if X and Y are related by a geometric transition, then it is expected that their mirrors
$X_{Q_{n,r}}$
are related by (a natural generalization of) a geometric transition. In the Calabi–Yau threefold case, if X and Y are related by a geometric transition, then it is expected that their mirrors
![]() $X^{\vee }$
and
$X^{\vee }$
and
![]() $Y^{\vee }$
are also related by a geometric transition, with the roles of the birational contraction and the smoothing reversed. We see the same phenomenon here.
$Y^{\vee }$
are also related by a geometric transition, with the roles of the birational contraction and the smoothing reversed. We see the same phenomenon here.
Recall that the vertices of
![]() $P_{n,r}$
are indexed by arrows in the ladder quiver. The vertices of
$P_{n,r}$
are indexed by arrows in the ladder quiver. The vertices of
![]() $Q_{n,r}$
are indexed by partitions
$Q_{n,r}$
are indexed by partitions
![]() $\lambda \in {\mathcal {P}(n,r)}.$
As before, set
$\lambda \in {\mathcal {P}(n,r)}.$
As before, set
![]() $k:=n-r$
. We will need to consider a set of special partitions in
$k:=n-r$
. We will need to consider a set of special partitions in
![]() ${\mathcal {P}(n,r)}$
. Define:
${\mathcal {P}(n,r)}$
. Define:
-
1.
 $\mu _{a,b}=(\underbrace {k,\dots ,k}_{a \text { times}},b)$
, where
$\mu _{a,b}=(\underbrace {k,\dots ,k}_{a \text { times}},b)$
, where
 $0 \leq a \leq r$
and
$0 \leq a \leq r$
and
 $0 \leq b \leq k$
.
$0 \leq b \leq k$
. -
2.
 $\nu _{a,b}$
to be the partition such that its transpose is
$\nu _{a,b}$
to be the partition such that its transpose is
 $\nu _{a,b}^t=(\underbrace {r,\dots ,r}_{a \text { times}},b)$
, where
$\nu _{a,b}^t=(\underbrace {r,\dots ,r}_{a \text { times}},b)$
, where
 $0 \leq a \leq k$
and
$0 \leq a \leq k$
and
 $0 \leq b \leq r$
.
$0 \leq b \leq r$
.
We will assign a partition
![]() $\mu _{a,b}$
or
$\mu _{a,b}$
or
![]() $\nu _{a,b}$
to each arrow in the dual quiver. This is equivalent to assigning such a partition to each arrow in the ladder quiver since each arrow in the dual quiver crosses precisely one arrow in the ladder quiver. It is easiest to see how the arrows are assigned in an example—see Figure 1.
$\nu _{a,b}$
to each arrow in the dual quiver. This is equivalent to assigning such a partition to each arrow in the ladder quiver since each arrow in the dual quiver crosses precisely one arrow in the ladder quiver. It is easiest to see how the arrows are assigned in an example—see Figure 1.

Figure 1 The labeling for
![]() $n=7$
,
$n=7$
,
![]() $r=3$
.
$r=3$
.
The following rules describe the assignment in general:
-
○ To the arrow with source an external vertex, we assign the maximal partition
 $(k^r)$
. To the arrow with target an external vertex, we assign
$(k^r)$
. To the arrow with target an external vertex, we assign
 $\varnothing $
.
$\varnothing $
. -
○ There are r rows of horizontal arrows with internal vertices, with each row containing
 $k-1$
arrows. To the
$k-1$
arrows. To the
 $a^{th}$
arrow (from the right) in the
$a^{th}$
arrow (from the right) in the
 $b^{th}$
row (from the bottom) of horizontal arrows, we assign
$b^{th}$
row (from the bottom) of horizontal arrows, we assign
 $\nu _{a,b-1}$
.
$\nu _{a,b-1}$
. -
○ There are k columns of vertical arrows, with each row containing
 $r-1$
arrows. To the
$r-1$
arrows. To the
 $a^{th}$
arrow (from the bottom) in the
$a^{th}$
arrow (from the bottom) in the
 $b^{th}$
column (from the right) of vertical arrows, we assign
$b^{th}$
column (from the right) of vertical arrows, we assign
 $\mu _{a-1,b}$
.
$\mu _{a-1,b}$
.
This defines a map from the arrows of the ladder quiver to
![]() ${\mathcal {P}(n,r)}$
, which we call
${\mathcal {P}(n,r)}$
, which we call
![]() $\phi :\operatorname {{\mathrm {LQ}}}_1 \to {\mathcal {P}(n,r)}$
.
$\phi :\operatorname {{\mathrm {LQ}}}_1 \to {\mathcal {P}(n,r)}$
.
Definition 3.2. A partition
![]() $\lambda \in {\mathcal {P}(n,r)}$
is an arrow partition if it is in the image of
$\lambda \in {\mathcal {P}(n,r)}$
is an arrow partition if it is in the image of
![]() $\phi : \operatorname {{\mathrm {LQ}}}_1 \to {\mathcal {P}(n,r)}$
, that is, if it is of the form:
$\phi : \operatorname {{\mathrm {LQ}}}_1 \to {\mathcal {P}(n,r)}$
, that is, if it is of the form:
-
1.
 $\nu _{a,b-1}$
, for
$\nu _{a,b-1}$
, for
 $1 \leq a \leq k$
and
$1 \leq a \leq k$
and
 $1 \leq b \leq r-1$
.
$1 \leq b \leq r-1$
. -
2.
 $\mu _{a-1,b}$
for
$\mu _{a-1,b}$
for
 $1 \leq a \leq r$
and
$1 \leq a \leq r$
and
 $1 \leq b \leq k-1$
.
$1 \leq b \leq k-1$
.
The set of arrow partitions is denoted
![]() ${\mathcal {A}(n,r)}$
. Its complement in
${\mathcal {A}(n,r)}$
. Its complement in
![]() ${\mathcal {P}(n,r)}$
is labeled
${\mathcal {P}(n,r)}$
is labeled
![]() ${\mathcal {B}(n,r)}$
; partitions in
${\mathcal {B}(n,r)}$
; partitions in
![]() ${\mathcal {B}(n,r)}$
are called excess partitions.
${\mathcal {B}(n,r)}$
are called excess partitions.
There are
![]() $2(r-1)(n-r-1)+n$
arrow partitions.
$2(r-1)(n-r-1)+n$
arrow partitions.
Example 3.3. Let
![]() $r=3$
,
$r=3$
,
![]() $n=6$
. Then
$n=6$
. Then
Lemma 3.4. Consider a path in the dual quiver between the two external vertices. The set of partitions given by the labels of the arrows in the path are the set of partitions associated to some crossing diagram.
Proof. We say that two partitions are crossing-diagram compatible if they can both appear in the same crossing diagram. Fix a dual arrow a, and consider all arrows in the dual quiver strictly to the right and below a (i.e., all arrows that could appear after a in a path on the dual quiver). Suppose a is vertical so that
![]() $\phi (a)$
is of the form
$\phi (a)$
is of the form

The two outgoing dual arrows from
![]() $t(a)$
have the labels drawn in orange and yellow below and hence are each crossing-diagram compatible with
$t(a)$
have the labels drawn in orange and yellow below and hence are each crossing-diagram compatible with
![]() $\phi (a)$
.
$\phi (a)$
.

Since all other arrows below and to the right of a have labels obtained by iteratively removing single boxes and complete rows or columns from these two, they are all also crossing-diagram compatible with
![]() $\phi (a)$
. The same analysis shows the same statement for a horizontal. If we now take a path between the two external vertices of the dual quiver, it is clear that all of the labels along the path are contained in the same crossing diagram, and since there are n of them, they are precisely the set of partitions associated to this crossing diagram.
$\phi (a)$
. The same analysis shows the same statement for a horizontal. If we now take a path between the two external vertices of the dual quiver, it is clear that all of the labels along the path are contained in the same crossing diagram, and since there are n of them, they are precisely the set of partitions associated to this crossing diagram.
The polytopes
![]() $P_{n,r}$
and
$P_{n,r}$
and
![]() $Q_{n,r}$
are closely related. Recall that the vertices of
$Q_{n,r}$
are closely related. Recall that the vertices of
![]() $Q_{n,r}$
are given by
$Q_{n,r}$
are given by
![]() $v_{\lambda }$
,
$v_{\lambda }$
,
![]() $\lambda \in {\mathcal {P}(n,r)}$
.
$\lambda \in {\mathcal {P}(n,r)}$
.
Theorem 3.5. Let
![]() $\overline {Q}_{n,r}$
be the polytope obtained by deleting the vertices of
$\overline {Q}_{n,r}$
be the polytope obtained by deleting the vertices of
![]() $Q_{n,r}$
associated to the excess partitions, that is,
$Q_{n,r}$
associated to the excess partitions, that is,
![]() $\overline {Q}_{n,r}$
is the convex hull of
$\overline {Q}_{n,r}$
is the convex hull of
![]() $\{v_{\lambda } : \lambda \in {\mathcal {A}(n,r)}\}$
. Then
$\{v_{\lambda } : \lambda \in {\mathcal {A}(n,r)}\}$
. Then
![]() $P_{n,r}$
and
$P_{n,r}$
and
![]() $\overline {Q}_{n,r}$
are isomorphic as lattice polytopes.
$\overline {Q}_{n,r}$
are isomorphic as lattice polytopes.
Proof. To prove the statement, it suffices to show
-
1. that
 $\overline {Q}_{n,r}$
is a Fano polytope (that is, it has primitive vertices and the origin is in its strict interior);
$\overline {Q}_{n,r}$
is a Fano polytope (that is, it has primitive vertices and the origin is in its strict interior); -
2. that both polytopes have vertices that span the ambient lattice;
-
3. that the associated toric varieties
 $X_{P_{n,r}}$
and
$X_{P_{n,r}}$
and
 $X_{\overline {Q}_{n,r}}$
have the same weight matrix.
$X_{\overline {Q}_{n,r}}$
have the same weight matrix.
We will first show a claim that will help with all three statements.
Since
![]() $\overline {Q}_{n,r}$
is obtained from
$\overline {Q}_{n,r}$
is obtained from
![]() $Q_{n,r}$
by forgetting some vertices, relations between vertices in the former are just given by relations between vertices in the latter that do not involve any of the forgotten vertices. We will describe a crossing diagram—which in particular is a relation between the vertices of
$Q_{n,r}$
by forgetting some vertices, relations between vertices in the former are just given by relations between vertices in the latter that do not involve any of the forgotten vertices. We will describe a crossing diagram—which in particular is a relation between the vertices of
![]() $Q_{n,r}$
—for each nonsource vertex in the ladder quiver, such that all associated paths are in
$Q_{n,r}$
—for each nonsource vertex in the ladder quiver, such that all associated paths are in
![]() ${\mathcal {A}(n,r)}$
.
${\mathcal {A}(n,r)}$
.
Claim 3.6. Fix a nonsource vertex v. Then the set
![]() $\{\phi (a): b_{va}=1\}$
is precisely the set of paths for some crossing diagram.
$\{\phi (a): b_{va}=1\}$
is precisely the set of paths for some crossing diagram.
Proof of claim
We have described the set
![]() $\{\phi (a): b_{va}=1\}$
in Example 2.3. It will be more convenient if we dualize the picture given there: The highlighted vertex (if internal) becomes a square in the dual quiver, and the highlighted arrows correspond to highlighted dual arrows. In the case of the external vertex, no square is highlighted. The diagrams then become
$\{\phi (a): b_{va}=1\}$
in Example 2.3. It will be more convenient if we dualize the picture given there: The highlighted vertex (if internal) becomes a square in the dual quiver, and the highlighted arrows correspond to highlighted dual arrows. In the case of the external vertex, no square is highlighted. The diagrams then become


and this generalizes easily to arbitrary n and r. The important thing to see from this picture is that the collection of dual arrows satisfying
![]() $b_{va}=1$
forms a path between the external vertices of the dual quiver. Therefore, by Lemma 3.4, the set of labels are the partitions for a crossing diagram.
$b_{va}=1$
forms a path between the external vertices of the dual quiver. Therefore, by Lemma 3.4, the set of labels are the partitions for a crossing diagram.
Claim 3.6 implies that the weight matrix of
![]() $X_{\overline {Q}_{n,r}}$
contains all of the rows of the weight matrix
$X_{\overline {Q}_{n,r}}$
contains all of the rows of the weight matrix
![]() $X_{P_{n,r}}$
, although there may be additional rows (such as those covering from k-coverings for
$X_{P_{n,r}}$
, although there may be additional rows (such as those covering from k-coverings for
![]() $k \geq 2$
).
$k \geq 2$
).
We need now to show that
![]() $\overline {Q}_{n,r}$
is a Fano polytope with vertices that span the lattice: We already know that this holds for
$\overline {Q}_{n,r}$
is a Fano polytope with vertices that span the lattice: We already know that this holds for
![]() $P_{n,r}$
. Note that the vertices of
$P_{n,r}$
. Note that the vertices of
![]() $\overline {Q}_{n,r}$
are primitive lattice vectors, as they are also vertices of the reflexive polytope
$\overline {Q}_{n,r}$
are primitive lattice vectors, as they are also vertices of the reflexive polytope
![]() $Q_{n,r}$
. For every vertex
$Q_{n,r}$
. For every vertex
![]() $v_{\lambda }$
of
$v_{\lambda }$
of
![]() $\overline {Q}_{n,r}$
, there is at least one crossing diagram of the form in Claim 3.6 which has
$\overline {Q}_{n,r}$
, there is at least one crossing diagram of the form in Claim 3.6 which has
![]() $\lambda $
as a path, and this implies that there exist positive
$\lambda $
as a path, and this implies that there exist positive
![]() $c_{\lambda }$
such that
$c_{\lambda }$
such that
Thus,
![]() $0$
lies in the strict interior of
$0$
lies in the strict interior of
![]() $\overline {Q}_{n,r}$
. To see that the vertices span the lattice, note that it suffices to check that the
$\overline {Q}_{n,r}$
. To see that the vertices span the lattice, note that it suffices to check that the
![]() $m_{\lambda }$
,
$m_{\lambda }$
,
![]() $\lambda \in {\mathcal {A}(n,r)}$
span the lattice N: This follows from the explicit description of the
$\lambda \in {\mathcal {A}(n,r)}$
span the lattice N: This follows from the explicit description of the
![]() $m_{\lambda }$
in equation (4). We leave the details here to the reader. It follows that
$m_{\lambda }$
in equation (4). We leave the details here to the reader. It follows that
![]() $\overline {Q}_{n,r}$
is an
$\overline {Q}_{n,r}$
is an
![]() $r(n-r)$
-dimensional Fano polytope, with the same number of vertices as
$r(n-r)$
-dimensional Fano polytope, with the same number of vertices as
![]() $P_{n,r}$
. Therefore, there can be no more relations between the vertices then those already found—we have already found
$P_{n,r}$
. Therefore, there can be no more relations between the vertices then those already found—we have already found
![]() $V - r(n-r)$
relations, where V is the number of vertices of
$V - r(n-r)$
relations, where V is the number of vertices of
![]() $\overline {Q}_{n,r}$
, and we know these relations are linearly independent because they are also relations for
$\overline {Q}_{n,r}$
, and we know these relations are linearly independent because they are also relations for
![]() $P_{n,r}$
—so the weight matrices are the same.
$P_{n,r}$
—so the weight matrices are the same.
Since we are only interested in studying
![]() $P_{n,r}$
up to isomorphism, we can replace
$P_{n,r}$
up to isomorphism, we can replace
![]() $P_{n,r}$
with
$P_{n,r}$
with
![]() $\overline {Q}_{n,r}$
and view
$\overline {Q}_{n,r}$
and view
![]() $P_{n,r}$
as a polytope in N with vertices indexed by
$P_{n,r}$
as a polytope in N with vertices indexed by
![]() $\lambda \in {\mathcal {A}(n,r)}$
.
$\lambda \in {\mathcal {A}(n,r)}$
.
Theorem 3.5 tells us that
![]() $Q_{n,r}$
is obtained from
$Q_{n,r}$
is obtained from
![]() $P_{n,r}$
by adding vertices. This has the effect of blowing up the spanning fan
$P_{n,r}$
by adding vertices. This has the effect of blowing up the spanning fan
![]() $F_{P_{n,r}}$
of
$F_{P_{n,r}}$
of
![]() $P_{n,r}$
along the missing rays (in some order). Label the partitions in
$P_{n,r}$
along the missing rays (in some order). Label the partitions in
![]() ${\mathcal {B}(n,r)}$
as
${\mathcal {B}(n,r)}$
as
![]() $\lambda _1,\dots ,\lambda _m$
, and set
$\lambda _1,\dots ,\lambda _m$
, and set
![]() $v_i:=v_{\lambda _i}\in N$
. Blowing up the spanning fan of
$v_i:=v_{\lambda _i}\in N$
. Blowing up the spanning fan of
![]() $P_{n,r}$
(viewed as a polytope in
$P_{n,r}$
(viewed as a polytope in
![]() $N_{\mathbb {R}}$
) repeatedly at
$N_{\mathbb {R}}$
) repeatedly at
![]() $v_1,\dots ,v_m$
, we obtain a new fan, and hence a new toric variety, which was called
$v_1,\dots ,v_m$
, we obtain a new fan, and hence a new toric variety, which was called
![]() $Y_{n,r}$
in the introduction.
$Y_{n,r}$
in the introduction.
Theorem 3.7. There is a variation of GIT from the weak Fano variety
![]() $Y_{n,r}$
to
$Y_{n,r}$
to
![]() $X_{Q_{n,r}}$
. The anticanonical polytope of these two toric varieties are equal, and they have isomorphic Cox rings. In particular,
$X_{Q_{n,r}}$
. The anticanonical polytope of these two toric varieties are equal, and they have isomorphic Cox rings. In particular,
![]() $\Gamma (\mathcal {O}_{-K_{Y_{n,r}}})=\Gamma (\mathcal {O}_{-K_{X_{Q_{n,r}}}}).$
$\Gamma (\mathcal {O}_{-K_{Y_{n,r}}})=\Gamma (\mathcal {O}_{-K_{X_{Q_{n,r}}}}).$
Proof. It follows from Theorem 3.5 that the GIT description of
![]() $Y_{n,r}$
and
$Y_{n,r}$
and
![]() $X_{Q_{n,r}}$
has the same weight matrix—that is, the fans have the same rays. The difference lies entirely in the choice of stability condition, which gives the different fan structure. The dual of the anticanonical polytope is the polytope spanned by primitive generators of the rays of the fan, so the anticanonical polytope of both toric varieties agree. In particular since this polyhedron is convex, we have that the anticanonical bundle of
$X_{Q_{n,r}}$
has the same weight matrix—that is, the fans have the same rays. The difference lies entirely in the choice of stability condition, which gives the different fan structure. The dual of the anticanonical polytope is the polytope spanned by primitive generators of the rays of the fan, so the anticanonical polytope of both toric varieties agree. In particular since this polyhedron is convex, we have that the anticanonical bundle of
![]() $Y_{n,r}$
is nef; that is,
$Y_{n,r}$
is nef; that is,
![]() $Y_{n,r}$
is weak Fano. The Cox ring of a toric variety depends only on the rays of the fan, so the last two claims follow immediately.
$Y_{n,r}$
is weak Fano. The Cox ring of a toric variety depends only on the rays of the fan, so the last two claims follow immediately.
4 Smoothing
In this section, we will discuss (partial) smoothings of
![]() $X_{P_{n,r}}/G$
and of
$X_{P_{n,r}}/G$
and of
![]() $Y_{n,r}/G$
.
$Y_{n,r}/G$
.
4.1 Smoothing
 $X_{P_{n,r}}/G$
$X_{P_{n,r}}/G$
Although the group action of G on
![]() $X_{P_{n,r}}$
looks very toric and unconnected to the Grassmannian, remarkably, when smoothing, we obtain a very natural group action on
$X_{P_{n,r}}$
looks very toric and unconnected to the Grassmannian, remarkably, when smoothing, we obtain a very natural group action on
![]() $\operatorname {{\mathrm {Gr}}}(n,r)$
, which generalizes the Greene–Plesser group action for projective space. Recall that
$\operatorname {{\mathrm {Gr}}}(n,r)$
, which generalizes the Greene–Plesser group action for projective space. Recall that
acts naturally on
![]() $\operatorname {{\mathrm {Mat}}}(r \times n)$
and descends to an effective action of
$\operatorname {{\mathrm {Mat}}}(r \times n)$
and descends to an effective action of
![]() $H_{n,r}$
on
$H_{n,r}$
on
![]() $\operatorname {{\mathrm {Gr}}}(n,r)$
. The group
$\operatorname {{\mathrm {Gr}}}(n,r)$
. The group
![]() $H_{n,r}$
is the quotient
$H_{n,r}$
is the quotient
4.1.1 The action of G on
 $X_{P_{n,r}}$
$X_{P_{n,r}}$
It follows from Lemma 1.9 that
![]() $G \cong (\mathbb {Z}/n\mathbb {Z})^{rk-1}$
, where, as before,
$G \cong (\mathbb {Z}/n\mathbb {Z})^{rk-1}$
, where, as before,
![]() $k=n-r$
. The group action of G on
$k=n-r$
. The group action of G on
![]() $X_{P_{n,r}}$
can be described as a quotient of a larger group action on
$X_{P_{n,r}}$
can be described as a quotient of a larger group action on
![]() ${\mathbb {C}}^{|\operatorname {{\mathrm {LQ}}}_1|}$
, recalling that
${\mathbb {C}}^{|\operatorname {{\mathrm {LQ}}}_1|}$
, recalling that
![]() $X_{P_{n,r}}={\mathbb {C}}^{|LQ_1|}/\!/ T$
,
$X_{P_{n,r}}={\mathbb {C}}^{|LQ_1|}/\!/ T$
,
![]() $T=({\mathbb {C}}^*)^{|\overline {\operatorname {{\mathrm {LQ}}}}_0|}$
. The group
$T=({\mathbb {C}}^*)^{|\overline {\operatorname {{\mathrm {LQ}}}}_0|}$
. The group
acts naturally via
![]() $\operatorname {{\mathrm {SL}}}(|\operatorname {{\mathrm {LQ}}}_1|)$
on
$\operatorname {{\mathrm {SL}}}(|\operatorname {{\mathrm {LQ}}}_1|)$
on
![]() ${\mathbb {C}}^{|\operatorname {{\mathrm {LQ}}}_1|}$
. The action descends to give an effective action of the quotient
${\mathbb {C}}^{|\operatorname {{\mathrm {LQ}}}_1|}$
. The action descends to give an effective action of the quotient
on the toric variety
![]() $X_{P_{n,r}}$
. To compute the intersection, we view both T and
$X_{P_{n,r}}$
. To compute the intersection, we view both T and
![]() $\tilde {G}$
as diagonal subgroups of
$\tilde {G}$
as diagonal subgroups of
![]() $\operatorname {{\mathrm {GL}}}(|\operatorname {{\mathrm {LQ}}}_1|)$
. Recall from equation (3) that the weight matrix of the toric variety is
$\operatorname {{\mathrm {GL}}}(|\operatorname {{\mathrm {LQ}}}_1|)$
. Recall from equation (3) that the weight matrix of the toric variety is
![]() $B:=[b_{va}]_{v \in \overline {\operatorname {{\mathrm {LQ}}}}_0, a \in \operatorname {{\mathrm {LQ}}}_1}$
. The intersection
$B:=[b_{va}]_{v \in \overline {\operatorname {{\mathrm {LQ}}}}_0, a \in \operatorname {{\mathrm {LQ}}}_1}$
. The intersection
![]() $T \cap \tilde {G}$
is generated by
$T \cap \tilde {G}$
is generated by
Remark 4.1. One way to see that this group action agrees with the action described in Lemma 1.9 is to convert the fan description of
![]() $X_{Q_{n,r}^{\vee }}$
to a GIT description. Recall that the vertices of
$X_{Q_{n,r}^{\vee }}$
to a GIT description. Recall that the vertices of
![]() $X_{Q_{n,r}^{\vee }}$
are indexed by arrows of the ladder diagram and that
$X_{Q_{n,r}^{\vee }}$
are indexed by arrows of the ladder diagram and that
![]() $Q_{n,r}^{\vee }$
can be obtained from the polytope of a divisor of
$Q_{n,r}^{\vee }$
can be obtained from the polytope of a divisor of
![]() $X_{Q_{n,r}}$
, namely the divisor associated to the empty partition. Let
$X_{Q_{n,r}}$
, namely the divisor associated to the empty partition. Let
![]() $m_a$
,
$m_a$
,
![]() $a \in \operatorname {{\mathrm {LQ}}}_1$
, denote the vertices of the polytope of this divisor. Then the vertices of
$a \in \operatorname {{\mathrm {LQ}}}_1$
, denote the vertices of the polytope of this divisor. Then the vertices of
![]() $Q_{n,r}^{\vee }$
are given by
$Q_{n,r}^{\vee }$
are given by
![]() $w_a:=n m_a-h$
, where h is a (fixed) primitive lattice vector and
$w_a:=n m_a-h$
, where h is a (fixed) primitive lattice vector and
![]() $a \in \operatorname {{\mathrm {LQ}}}_1$
.
$a \in \operatorname {{\mathrm {LQ}}}_1$
.
The rays of the fan of
![]() $X_{Q_{n,r}^{\vee }}$
do not generate the ambient lattice. To convert to the GIT description, we must add virtual rays—rays that appear in no cones of the fan—so that all the rays together generate the lattice. It suffices to add all of the
$X_{Q_{n,r}^{\vee }}$
do not generate the ambient lattice. To convert to the GIT description, we must add virtual rays—rays that appear in no cones of the fan—so that all the rays together generate the lattice. It suffices to add all of the
![]() $m_a$
as virtual rays. Then in addition to the weights of
$m_a$
as virtual rays. Then in addition to the weights of
![]() $X_{P_{n,r}}$
, we also obtain gradings coming from the relations
$X_{P_{n,r}}$
, we also obtain gradings coming from the relations
Choosing an appropriate stability condition allows us to translate these gradings into quotient gradings, which exactly give the action of
![]() $\tilde {G}$
on
$\tilde {G}$
on
![]() ${\mathbb {C}}^{|\operatorname {{\mathrm {LQ}}}_1|}$
.
${\mathbb {C}}^{|\operatorname {{\mathrm {LQ}}}_1|}$
.
4.1.2 The action of G on
 $\mathbb {P}^{\binom {n}{r}-1}$
$\mathbb {P}^{\binom {n}{r}-1}$
The embedding of
![]() $X_{P_{n,r}}$
into
$X_{P_{n,r}}$
into
![]() $\mathbb {P}^{\binom {n}{r}-1}$
allows us to extend the action of G to
$\mathbb {P}^{\binom {n}{r}-1}$
allows us to extend the action of G to
![]() $\mathbb {P}^{\binom {n}{r}-1}$
. Label the coordinates of
$\mathbb {P}^{\binom {n}{r}-1}$
. Label the coordinates of
![]() $\mathbb {P}^{\binom {n}{r}-1}$
by
$\mathbb {P}^{\binom {n}{r}-1}$
by
![]() $p_{\lambda }$
,
$p_{\lambda }$
,
![]() $\lambda \in {\mathcal {P}(n,r)}$
. These are of course the Plücker coordinates—recall that they can be indexed either by partitions in
$\lambda \in {\mathcal {P}(n,r)}$
. These are of course the Plücker coordinates—recall that they can be indexed either by partitions in
![]() ${\mathcal {P}(n,r)}$
or by size-r subsets of
${\mathcal {P}(n,r)}$
or by size-r subsets of
![]() $\{1,\dots ,n\}$
(Definition 2.4). For a partition
$\{1,\dots ,n\}$
(Definition 2.4). For a partition
![]() $\lambda \in {\mathcal {P}(n,r)}$
,
$\lambda \in {\mathcal {P}(n,r)}$
,
![]() $I_{\lambda }$
denotes the corresponding subset.
$I_{\lambda }$
denotes the corresponding subset.
The embedding is given by the
![]() $\binom {n}{r}$
sections of
$\binom {n}{r}$
sections of
![]() $\mathcal {O}(1)$
on
$\mathcal {O}(1)$
on
![]() $X_{P_{n,r}}$
, that is,
$X_{P_{n,r}}$
, that is,
The group
![]() $\tilde {G}$
acts on the coordinate
$\tilde {G}$
acts on the coordinate
![]() $p_{\lambda }$
by multiplication by
$p_{\lambda }$
by multiplication by
![]() $\prod _{a \in \lambda } \psi _a.$
Either by observing that it is true by construction of the embedding or by explicitly checking, it is easy to see that the action of
$\prod _{a \in \lambda } \psi _a.$
Either by observing that it is true by construction of the embedding or by explicitly checking, it is easy to see that the action of
![]() $\tilde {G}$
descends to an action of G on
$\tilde {G}$
descends to an action of G on
![]() $\mathbb {P}^{\binom {n}{r}-1}$
. That is, elements of intersection
$\mathbb {P}^{\binom {n}{r}-1}$
. That is, elements of intersection
![]() $T \cap \tilde {G}$
act by scaling.
$T \cap \tilde {G}$
act by scaling.
4.1.3 Degenerate Plücker relations
The toric variety
![]() $X_{P_{n,r}}$
is cut out of
$X_{P_{n,r}}$
is cut out of
![]() $\mathbb {P}^{\binom {n}{r}-1}$
by degenerate Plücker relations [Reference Batyrev, Ciocan-Fontanine, Kim and van Straten3].
$\mathbb {P}^{\binom {n}{r}-1}$
by degenerate Plücker relations [Reference Batyrev, Ciocan-Fontanine, Kim and van Straten3].
Definition 4.2. Let
![]() $\prec $
be the usual partial order on partitions/Plücker coordinates: for
$\prec $
be the usual partial order on partitions/Plücker coordinates: for
![]() $\lambda $
,
$\lambda $
,
![]() $\sigma \in {\mathcal {P}(n,r)}$
,
$\sigma \in {\mathcal {P}(n,r)}$
,
![]() $\lambda \prec \sigma $
if
$\lambda \prec \sigma $
if
![]() $\lambda _i \leq \sigma _i$
for all i. Here, we use zeroes to extend any partition in
$\lambda _i \leq \sigma _i$
for all i. Here, we use zeroes to extend any partition in
![]() ${\mathcal {P}(n,r)}$
to a length-r partition.
${\mathcal {P}(n,r)}$
to a length-r partition.
Following [Reference Batyrev, Ciocan-Fontanine, Kim and van Straten3], there is a relation for every incomparable pair of partitions
![]() $\lambda $
,
$\lambda $
,
![]() $\sigma $
:
$\sigma $
:
Here,
![]() $\sigma \wedge \lambda $
is the minimal partition
$\sigma \wedge \lambda $
is the minimal partition
![]() $\mu $
satisfying
$\mu $
satisfying
![]() $\lambda , \sigma \prec \mu $
and
$\lambda , \sigma \prec \mu $
and
![]() $\sigma \vee \lambda $
is the maximal partition
$\sigma \vee \lambda $
is the maximal partition
![]() $\nu $
satisfying
$\nu $
satisfying
![]() $\nu \prec \lambda ,\sigma .$
$\nu \prec \lambda ,\sigma .$
Example 4.3. We give an example for
![]() $Gr(7,3)$
. The partitions
$Gr(7,3)$
. The partitions
![]() $\sigma =(1,1,1)$
and
$\sigma =(1,1,1)$
and
![]() $\lambda =(4,2)$
are incomparable. We draw them in blue and green, respectively, below.
$\lambda =(4,2)$
are incomparable. We draw them in blue and green, respectively, below.

The partition
![]() $\sigma \vee \lambda $
is drawn in red and
$\sigma \vee \lambda $
is drawn in red and
![]() $\sigma \wedge \lambda $
in yellow.
$\sigma \wedge \lambda $
in yellow.

Lemma 4.4. The degenerate Plücker relations are homogeneous with respect to the induced action of G on
![]() $\mathbb {P}^{\binom {n}{r}-1}$
.
$\mathbb {P}^{\binom {n}{r}-1}$
.
Proof. Let
![]() $\sigma $
,
$\sigma $
,
![]() $\lambda $
be an incomparable pair. The set of arrows contained in the union of
$\lambda $
be an incomparable pair. The set of arrows contained in the union of
![]() $\sigma $
and
$\sigma $
and
![]() $\lambda $
is the same as the set of arrows contained in the union of
$\lambda $
is the same as the set of arrows contained in the union of
![]() $\sigma \vee \lambda $
and
$\sigma \vee \lambda $
and
![]() $\sigma \wedge \lambda $
. Therefore, G acts with the same weights on
$\sigma \wedge \lambda $
. Therefore, G acts with the same weights on
![]() $p_{\sigma } p_{\lambda }$
and
$p_{\sigma } p_{\lambda }$
and
![]() $p_{\sigma \wedge \lambda } p_{\sigma \vee \lambda }.$
$p_{\sigma \wedge \lambda } p_{\sigma \vee \lambda }.$
4.1.4 The group preserving the Plücker relations
Consider the Plücker relation for
![]() $\operatorname {{\mathrm {Gr}}}(4,2)$
:
$\operatorname {{\mathrm {Gr}}}(4,2)$
:
which degenerates to
The second equation is homogeneous under the action of G, but the first is not. However, it is homogeneous with respect to a subgroup of G.
Definition 4.5. Let
![]() $G_h$
be the subgroup of G that preserves the Grassmannian, that is,
$G_h$
be the subgroup of G that preserves the Grassmannian, that is,
![]() $G_h$
is the largest subgroup of G such that all Plücker relations are homogeneous with respect to this action.
$G_h$
is the largest subgroup of G such that all Plücker relations are homogeneous with respect to this action.
Before describing
![]() $G_h$
precisely, let’s describe it heuristically. Binomial Plücker relations are of the form:
$G_h$
precisely, let’s describe it heuristically. Binomial Plücker relations are of the form:
For a complete description of these relations, see [Reference Miller and Sturmfels19]. A term
![]() $p_{\alpha } p_{\beta }$
appears with nonzero coefficient only if the multisets
$p_{\alpha } p_{\beta }$
appears with nonzero coefficient only if the multisets
![]() $I_{\sigma } \cup I_{\lambda }$
and
$I_{\sigma } \cup I_{\lambda }$
and
![]() $I_{\alpha } \cup I_{\beta }$
agree. In other words, the terms that appear in the sum must just be rearrangements of the indices of
$I_{\alpha } \cup I_{\beta }$
agree. In other words, the terms that appear in the sum must just be rearrangements of the indices of
![]() $I_{\sigma }$
and
$I_{\sigma }$
and
![]() $I_{\lambda }$
. The Plücker relations are not homogeneous with respect to the action of G because this action feels the paths of the partitions, which is more precise than the location of the vertical steps (which gives the underlying subset). We are looking for a subgroup
$I_{\lambda }$
. The Plücker relations are not homogeneous with respect to the action of G because this action feels the paths of the partitions, which is more precise than the location of the vertical steps (which gives the underlying subset). We are looking for a subgroup
![]() $G_h$
whose action depends only on the indices. We will show that
$G_h$
whose action depends only on the indices. We will show that
![]() $G_h$
is isomorphic to
$G_h$
is isomorphic to
![]() $H_{n,r}$
. The first step is to define a map from
$H_{n,r}$
. The first step is to define a map from
![]() $H_{n,r}$
to G.
$H_{n,r}$
to G.
Consider the following labeling of the vertical steps of a ladder diagram:

The labeling allows assigning a subset of
![]() $\{1,\dots ,n\}$
to an arrow or path in the ladder diagram by recording the labels along the arrow or path. For example, the path corresponding to the partition
$\{1,\dots ,n\}$
to an arrow or path in the ladder diagram by recording the labels along the arrow or path. For example, the path corresponding to the partition
in the
![]() $\operatorname {{\mathrm {Gr}}}(2,5)$
diagram has labeling
$\operatorname {{\mathrm {Gr}}}(2,5)$
diagram has labeling
![]() $\{1,3\}$
. Some arrows are associated to the empty set—in this example, the internal horizontal arrow has no labels.
$\{1,3\}$
. Some arrows are associated to the empty set—in this example, the internal horizontal arrow has no labels.
The following remark is key to establishing the next two lemmas.
Remark 4.6. The labeling of a path
![]() $\lambda $
is
$\lambda $
is
![]() $I_{\lambda }$
.
$I_{\lambda }$
.
Use the labeling to define a morphism
 $$\begin{align*}\tilde{\Psi}: \tilde{H}_{n,r} \to \tilde{G}, \:\: (\zeta_i)_{i=1}^n \mapsto \left(\prod_{\substack{j \text{ a label} \\ \text{of } a}} \zeta_j\right)_{a \in \operatorname{{\mathrm{LQ}}}_1}. \end{align*}$$
$$\begin{align*}\tilde{\Psi}: \tilde{H}_{n,r} \to \tilde{G}, \:\: (\zeta_i)_{i=1}^n \mapsto \left(\prod_{\substack{j \text{ a label} \\ \text{of } a}} \zeta_j\right)_{a \in \operatorname{{\mathrm{LQ}}}_1}. \end{align*}$$
Lemma 4.7. The map
![]() $\tilde {\Psi }$
descends to an injective map
$\tilde {\Psi }$
descends to an injective map
![]() $\psi : H_{n,r} \to G.$
$\psi : H_{n,r} \to G.$
Proof. Recall that G acts on
![]() $\mathbb {P}^{\binom {n}{r}-1}$
. We know that
$\mathbb {P}^{\binom {n}{r}-1}$
. We know that
![]() $T \cap \tilde {G}$
acts on
$T \cap \tilde {G}$
acts on
![]() $\mathbb {P}^{\binom {n}{r}-1}$
by scaling, so it suffices to show that, for
$\mathbb {P}^{\binom {n}{r}-1}$
by scaling, so it suffices to show that, for
![]() $h \in \tilde {H}_{n,r}$
,
$h \in \tilde {H}_{n,r}$
,
Note that
 $$\begin{align*}\tilde{\Psi}((\zeta_i)_{i=1}^n)\cdot \left[p_{\lambda}: \lambda \in {\mathcal{P}(n,r)}\right]=\left[\left(\prod_{j \in I_{\lambda}} \zeta_j\right) p_{\lambda}: \lambda \in {\mathcal{P}(n,r)}\right]. \end{align*}$$
$$\begin{align*}\tilde{\Psi}((\zeta_i)_{i=1}^n)\cdot \left[p_{\lambda}: \lambda \in {\mathcal{P}(n,r)}\right]=\left[\left(\prod_{j \in I_{\lambda}} \zeta_j\right) p_{\lambda}: \lambda \in {\mathcal{P}(n,r)}\right]. \end{align*}$$
Since
![]() $I_{\lambda }$
runs over all size r subsets of
$I_{\lambda }$
runs over all size r subsets of
![]() $\{1,\dots ,n\}$
, the only way to ensure that
$\{1,\dots ,n\}$
, the only way to ensure that
 $$\begin{align*}\prod_{j \in I_{\lambda}} \zeta_j =\prod_{j \in I_{\mu}} \zeta_j \end{align*}$$
$$\begin{align*}\prod_{j \in I_{\lambda}} \zeta_j =\prod_{j \in I_{\mu}} \zeta_j \end{align*}$$
for all
![]() $\lambda $
,
$\lambda $
,
![]() $\mu $
is for
$\mu $
is for
![]() $\zeta _i=\zeta _j$
for all i, j.
$\zeta _i=\zeta _j$
for all i, j.
Lemma 4.8. The image of
![]() $H_{n,r}$
under
$H_{n,r}$
under
![]() $\Psi $
preserves the Grassmannian, that is,
$\Psi $
preserves the Grassmannian, that is,
Proof. Consider a binomial Plücker relation:
where the term
![]() $p_{\alpha } p_{\beta }$
appears with nonzero coefficient only if the multisets
$p_{\alpha } p_{\beta }$
appears with nonzero coefficient only if the multisets
![]() $I_{\sigma } \cup I_{\lambda }$
and
$I_{\sigma } \cup I_{\lambda }$
and
![]() $I_{\alpha } \cup I_{\beta }$
are equal. A group element
$I_{\alpha } \cup I_{\beta }$
are equal. A group element
![]() $\tilde {\Psi }((\zeta _i))$
acts on
$\tilde {\Psi }((\zeta _i))$
acts on
![]() $p_{\alpha } p_{\beta }$
by multiplication by
$p_{\alpha } p_{\beta }$
by multiplication by
 $$\begin{align*}\prod_{j \in I_{\alpha}} \zeta_j \prod_{j \in I_{\beta}} \zeta_j \end{align*}$$
$$\begin{align*}\prod_{j \in I_{\alpha}} \zeta_j \prod_{j \in I_{\beta}} \zeta_j \end{align*}$$
which is equal to
 $$\begin{align*}\prod_{j \in I_{\lambda}} \zeta_j \prod_{j \in I_{\sigma}} \zeta_j. \end{align*}$$
$$\begin{align*}\prod_{j \in I_{\lambda}} \zeta_j \prod_{j \in I_{\sigma}} \zeta_j. \end{align*}$$
Therefore, the relation is homogeneous with respect to the
![]() $\tilde {\Psi }(\tilde {G})$
action, and hence the
$\tilde {\Psi }(\tilde {G})$
action, and hence the
![]() $\Psi (G)$
action.
$\Psi (G)$
action.
The main combinatorial result of this section is the next theorem.
Theorem 4.9. There is an isomorphism
![]() $G_h \cong H_{n,r}$
.
$G_h \cong H_{n,r}$
.
Proof. The map
![]() $\Psi $
defines an isomorphism
$\Psi $
defines an isomorphism
![]() $H_{n,r} \to \Psi (H_{n,r})$
. We will show that
$H_{n,r} \to \Psi (H_{n,r})$
. We will show that
![]() $\Psi (H_{n,r})=G_h$
; by Lemma 4.8,
$\Psi (H_{n,r})=G_h$
; by Lemma 4.8,
![]() $\Psi (H_{n,r}) \subseteq G_h$
. We will show the other direction by demonstrating that, for every
$\Psi (H_{n,r}) \subseteq G_h$
. We will show the other direction by demonstrating that, for every
![]() $[g] \in G_h$
with lift
$[g] \in G_h$
with lift
![]() $g \in \tilde {G}$
, the
$g \in \tilde {G}$
, the
![]() $\tilde {G} \cap T$
-orbit of g has nonempty intersection with
$\tilde {G} \cap T$
-orbit of g has nonempty intersection with
![]() $\tilde {\Psi }(\tilde {H}_{n,r})$
. We will use two collections of arrows in the proof. The first collection
$\tilde {\Psi }(\tilde {H}_{n,r})$
. We will use two collections of arrows in the proof. The first collection
![]() $C_1$
is described via the following example: It is the set of
$C_1$
is described via the following example: It is the set of
![]() $n=9$
arrows that are fully contained in the blue part of the diagram.
$n=9$
arrows that are fully contained in the blue part of the diagram.

In general, there are n arrows in
![]() $C_1$
. We label them, starting at the bottom-left corner, by
$C_1$
. We label them, starting at the bottom-left corner, by
![]() $a^1_1,\dots ,a^1_n.$
This collection is chosen so that if
$a^1_1,\dots ,a^1_n.$
This collection is chosen so that if
![]() $(\psi _a) \in \tilde {\Psi }(\tilde {H}_{n,r})$
, then the
$(\psi _a) \in \tilde {\Psi }(\tilde {H}_{n,r})$
, then the
![]() $\psi _a$
,
$\psi _a$
,
![]() $a \not \in C_1$
are determined by the
$a \not \in C_1$
are determined by the
![]() $\psi _a$
,
$\psi _a$
,
![]() $a \in C_1$
. This is because the
$a \in C_1$
. This is because the
![]() $\psi _a$
,
$\psi _a$
,
![]() $a \in C_1$
, are
$a \in C_1$
, are
so that the exponent matrix of the map
![]() $\Psi $
composed with the projection
$\Psi $
composed with the projection
![]() $\pi :(\psi _a)_{a \in \operatorname {{\mathrm {LQ}}}_1} \mapsto (\psi _a)_{a \in C_1}$
is an invertible matrix in
$\pi :(\psi _a)_{a \in \operatorname {{\mathrm {LQ}}}_1} \mapsto (\psi _a)_{a \in C_1}$
is an invertible matrix in
![]() $\operatorname {{\mathrm {GL}}}(n,\mathbb {Z})$
. This means that, for
$\operatorname {{\mathrm {GL}}}(n,\mathbb {Z})$
. This means that, for
![]() $(\psi _a)_{a} \in \tilde {\Psi }(\tilde {H}_n,r)$
, we can express each
$(\psi _a)_{a} \in \tilde {\Psi }(\tilde {H}_n,r)$
, we can express each
![]() $\psi _a$
,
$\psi _a$
,
![]() $a \in \operatorname {{\mathrm {LQ}}}_1$
, as a function of the
$a \in \operatorname {{\mathrm {LQ}}}_1$
, as a function of the
![]() $\psi _a$
,
$\psi _a$
,
![]() $a \in C_1$
. Denote this function by
$a \in C_1$
. Denote this function by
![]() $\xi _a$
, which we view as a function on
$\xi _a$
, which we view as a function on
![]() $\tilde {G}$
that depends only on the
$\tilde {G}$
that depends only on the
![]() $\psi _a$
for
$\psi _a$
for
![]() $a \in C_1$
. Then the maps
$a \in C_1$
. Then the maps
![]() $\xi _a$
provide a way of measuring how far away an element of
$\xi _a$
provide a way of measuring how far away an element of
![]() $\tilde {G}$
is from being in the image of
$\tilde {G}$
is from being in the image of
![]() $\tilde {\Psi }(\tilde {H}_{n,r})$
:
$\tilde {\Psi }(\tilde {H}_{n,r})$
:
The second collection of arrows
![]() $C_2$
is drawn in green in the example below. It is disjoint from
$C_2$
is drawn in green in the example below. It is disjoint from
![]() $C_1$
.
$C_1$
.

Taking the target map from
![]() $C_2 \to \operatorname {{\mathrm {LQ}}}_0$
gives an injection.
$C_2 \to \operatorname {{\mathrm {LQ}}}_0$
gives an injection.
Claim 4.10. The
![]() $T \cap \tilde {G}$
orbit of any
$T \cap \tilde {G}$
orbit of any
![]() $g \in \tilde {G}$
contains another group element
$g \in \tilde {G}$
contains another group element
![]() $h=(\psi _a)_{a \in \operatorname {{\mathrm {LQ}}}_1}$
satisfying, for
$h=(\psi _a)_{a \in \operatorname {{\mathrm {LQ}}}_1}$
satisfying, for
![]() $a \in C_2$
:
$a \in C_2$
:
In other words, along
![]() $a \in C_2$
, the relations we need for h to be an element of
$a \in C_2$
, the relations we need for h to be an element of
![]() $\tilde {\Psi }(\tilde {H}_{n,r})$
are satisfied.
$\tilde {\Psi }(\tilde {H}_{n,r})$
are satisfied.
Proof of claim
There are two types of arrows in
![]() $C_2$
: horizontal arrows and arrows containing a vertical step, which we call vertical for simplicity. Each of the arrows in
$C_2$
: horizontal arrows and arrows containing a vertical step, which we call vertical for simplicity. Each of the arrows in
![]() $C_2$
picks out a column in the weight matrix
$C_2$
picks out a column in the weight matrix
![]() $[b_{va}]$
of
$[b_{va}]$
of
![]() $X_{{P_{n,r}}}$
. If we order the arrows in
$X_{{P_{n,r}}}$
. If we order the arrows in
![]() $C_1$
from left to right and top to bottom, the resulting submatrix of
$C_1$
from left to right and top to bottom, the resulting submatrix of
![]() $[b_{va}]$
is the identity matrix along the vertical arrows and then upper triangular for the rest with
$[b_{va}]$
is the identity matrix along the vertical arrows and then upper triangular for the rest with
![]() $1$
s on the diagonal.
$1$
s on the diagonal.
If a is horizontal, then the equation that h must satisfy is
Recall that the generators of
![]() $T \cap \tilde {G}$
are given by the rows of the weight matrix of the ladder quiver—there is a row for each vertex, and the entries are the
$T \cap \tilde {G}$
are given by the rows of the weight matrix of the ladder quiver—there is a row for each vertex, and the entries are the
![]() $b_{va}$
; see equation (6). Since the submatrix is upper triangular, we can use the generators of
$b_{va}$
; see equation (6). Since the submatrix is upper triangular, we can use the generators of
![]() $T \cap \tilde {G}$
corresponding to the vertices
$T \cap \tilde {G}$
corresponding to the vertices
![]() $t(a)$
, a horizontal, to move g within its orbit to a group element satisfying the equations we need for horizontal
$t(a)$
, a horizontal, to move g within its orbit to a group element satisfying the equations we need for horizontal
![]() $a \in C_2$
. Call this element
$a \in C_2$
. Call this element
![]() $g'=(\psi ^{\prime }_a)$
.
$g'=(\psi ^{\prime }_a)$
.
We now focus on the vertical arrows. Note that none of the generators of
![]() $T \cap \tilde {G}$
associated to the vertical arrows act nontrivially on the
$T \cap \tilde {G}$
associated to the vertical arrows act nontrivially on the
![]() $\psi _a$
,
$\psi _a$
,
![]() $a \in C_2$
, a horizontal. Label the vertical arrows of
$a \in C_2$
, a horizontal. Label the vertical arrows of
![]() $C_2$
from bottom to top as
$C_2$
from bottom to top as
![]() $a^2_1,\dots ,a^2_{r-1}$
. Then the equations that
$a^2_1,\dots ,a^2_{r-1}$
. Then the equations that
![]() $g'$
must satisfy are
$g'$
must satisfy are
To move g within its orbit so that it satisfies these equations, we start with the last vertical arrow,
![]() $a^2_{r-1}$
. If we act with the generator associated to
$a^2_{r-1}$
. If we act with the generator associated to
![]() $t(a^2_{r-1})$
, we can set the
$t(a^2_{r-1})$
, we can set the
![]() ${a^2_{r-1}}$
-th coordinate to
${a^2_{r-1}}$
-th coordinate to
Note that that generator acts nontrivially on the
![]() $a^1_{r}$
and
$a^1_{r}$
and
![]() $a^1_{r-1}$
coordinates—however, it acts on the same weight with each, so we now have a group element which satisfies the
$a^1_{r-1}$
coordinates—however, it acts on the same weight with each, so we now have a group element which satisfies the
![]() $a^2_{r_1}$
equation and the horizontal equations. If we move one step lower, the same thing happens: Our group element acts trivially on the ratios
$a^2_{r_1}$
equation and the horizontal equations. If we move one step lower, the same thing happens: Our group element acts trivially on the ratios
![]() $\psi ^{\prime }_{a^1_{r}}/\psi ^{\prime }_{a^1_{r-1}}$
and
$\psi ^{\prime }_{a^1_{r}}/\psi ^{\prime }_{a^1_{r-1}}$
and
![]() $\psi ^{\prime }_{a^1_{r-1}}/\psi ^{\prime }_{a^1_{r-2}}$
. Continuing downwards, eventually we find h as required.
$\psi ^{\prime }_{a^1_{r-1}}/\psi ^{\prime }_{a^1_{r-2}}$
. Continuing downwards, eventually we find h as required.
Let’s rephrase what we’ve done so far: For every
![]() $[g] \in G$
, we have identified a particular lift
$[g] \in G$
, we have identified a particular lift
![]() $g \in \tilde {G}$
satisfying
$g \in \tilde {G}$
satisfying
To complete the proof, it is enough to show that if
![]() $[g] \in G_h$
, then the special lift g constructed above is in
$[g] \in G_h$
, then the special lift g constructed above is in
![]() $\tilde {\Psi }(\tilde {H}_{n,r})$
. Since
$\tilde {\Psi }(\tilde {H}_{n,r})$
. Since
![]() $\tilde {G} \cap T$
acts trivially on the Plücker coordinates, both g and
$\tilde {G} \cap T$
acts trivially on the Plücker coordinates, both g and
![]() $[g]$
preserve the Plücker relations. In particular, g preserves certain three-term Plücker relations: We will define such a relation for every internal vertex in the ladder quiver.
$[g]$
preserve the Plücker relations. In particular, g preserves certain three-term Plücker relations: We will define such a relation for every internal vertex in the ladder quiver.
For every internal vertex
![]() $v \in \operatorname {{\mathrm {LQ}}}_0$
, fix an incomparable pair
$v \in \operatorname {{\mathrm {LQ}}}_0$
, fix an incomparable pair
![]() $\lambda _v$
,
$\lambda _v$
,
![]() $\sigma _v$
which crosses at v and agrees outside of the
$\sigma _v$
which crosses at v and agrees outside of the
![]() $2\times 2$
box centered at v. (The argument will not depend on what happens outside the
$2\times 2$
box centered at v. (The argument will not depend on what happens outside the
![]() $2 \times 2$
box centered at v.) For example, here are some pairs with v highlighted in red and the box shaded in gray.
$2 \times 2$
box centered at v.) For example, here are some pairs with v highlighted in red and the box shaded in gray.

Fix an interior vertex v. Locally about vertex v,
![]() $\lambda _v$
and
$\lambda _v$
and
![]() $\sigma _v$
look like:
$\sigma _v$
look like:

By definition,
![]() $\sigma _v \wedge \lambda _v$
and
$\sigma _v \wedge \lambda _v$
and
![]() $\sigma _v \vee \lambda _v$
agree with
$\sigma _v \vee \lambda _v$
agree with
![]() $\lambda _v, \sigma _v$
outside of the box centered at v, and locally at v they look like
$\lambda _v, \sigma _v$
outside of the box centered at v, and locally at v they look like

The incomparable pair
![]() $\sigma _v, \lambda _v$
gives rise to a three-term Plücker relation:
$\sigma _v, \lambda _v$
gives rise to a three-term Plücker relation:
The partitions
![]() $\alpha _v$
,
$\alpha _v$
,
![]() $\beta _v$
are characterized by agreeing with
$\beta _v$
are characterized by agreeing with
![]() $\sigma $
,
$\sigma $
,
![]() $\lambda $
outside of the box centered at v, and locally at v they look like
$\lambda $
outside of the box centered at v, and locally at v they look like

One can easily read off from this picture that this relation is homogeneous with respect to the
![]() $\Psi (H_{n,r})$
-action. Let
$\Psi (H_{n,r})$
-action. Let
![]() $S_{v}$
be the collection of arrows of
$S_{v}$
be the collection of arrows of
![]() $\operatorname {{\mathrm {LQ}}}$
whose intersection with the
$\operatorname {{\mathrm {LQ}}}$
whose intersection with the
![]() $2\times 2$
box in equation (9) is contained in the blue or green highlighted paths in equation (9). Let
$2\times 2$
box in equation (9) is contained in the blue or green highlighted paths in equation (9). Let
![]() $T_v$
be the collection of arrows of
$T_v$
be the collection of arrows of
![]() $\operatorname {{\mathrm {LQ}}}$
whose intersection with the
$\operatorname {{\mathrm {LQ}}}$
whose intersection with the
![]() $2 \times 2$
box in equation (10) is contained in the blue or green highlighted paths in equation (10). If
$2 \times 2$
box in equation (10) is contained in the blue or green highlighted paths in equation (10). If
![]() $g=(\psi _a) \in \tilde {G}$
preserves this relationship, then
$g=(\psi _a) \in \tilde {G}$
preserves this relationship, then
Now, fix some
![]() $[g] \in G_h$
with lift
$[g] \in G_h$
with lift
![]() $g \in \tilde {G} $
constructed as in equation (8). The Plücker relation constructed for any v is homogeneous for
$g \in \tilde {G} $
constructed as in equation (8). The Plücker relation constructed for any v is homogeneous for
![]() $g=(\psi _a)$
, so equation (11) holds for all v.
$g=(\psi _a)$
, so equation (11) holds for all v.
Consider the following diagram, which highlights both
![]() $C_1$
and
$C_1$
and
![]() $C_2$
.
$C_2$
.

Consider the top-left interior vertex
![]() $v_0$
. Note that there is precisely one arrow
$v_0$
. Note that there is precisely one arrow
![]() $a_0$
in
$a_0$
in
![]() $S_{v_0} \cup T_{v_0}$
that is not contained in
$S_{v_0} \cup T_{v_0}$
that is not contained in
![]() $C:=C_1 \cup C_2$
. Using equation (11) for
$C:=C_1 \cup C_2$
. Using equation (11) for
![]() $v_0$
one can see that
$v_0$
one can see that
![]() $\psi ^{\prime }_{a_0}$
is determined by the
$\psi ^{\prime }_{a_0}$
is determined by the
![]() $\psi _a$
,
$\psi _a$
,
![]() $a \in C$
—and so, in fact, is determined by the
$a \in C$
—and so, in fact, is determined by the
![]() $\psi _a$
,
$\psi _a$
,
![]() $a \in C_1$
. Abusing notation, replace C by
$a \in C_1$
. Abusing notation, replace C by
![]() $C \cup \{a_0\}$
. Now, consider the vertex
$C \cup \{a_0\}$
. Now, consider the vertex
![]() $v_1$
directly below
$v_1$
directly below
![]() $v_0$
, and note that there is precisely one arrow
$v_0$
, and note that there is precisely one arrow
![]() $a_1$
in
$a_1$
in
![]() $S_{v_1} \cup T_{v_1}$
that is not contained in (the new) C. Applying equation (11) for
$S_{v_1} \cup T_{v_1}$
that is not contained in (the new) C. Applying equation (11) for
![]() $v_1$
, we see that
$v_1$
, we see that
![]() $\psi ^{\prime }_{a_1}$
is determined by the
$\psi ^{\prime }_{a_1}$
is determined by the
![]() $\psi _a$
,
$\psi _a$
,
![]() $a \in C$
, and hence by
$a \in C$
, and hence by
![]() $\psi _a'$
,
$\psi _a'$
,
![]() $a \in C_1$
. Applying this argument repeatedly, moving down columns from left to right, we conclude that g is uniquely characterized by:
$a \in C_1$
. Applying this argument repeatedly, moving down columns from left to right, we conclude that g is uniquely characterized by:
-
○ the values
 $(\psi _a)_{a \in C_1}$
$(\psi _a)_{a \in C_1}$
-
○ equation (8)
-
○ preserving the Plücker relations.
We now use the
![]() $\psi _a$
,
$\psi _a$
,
![]() $a \in C_1$
, to define an element of
$a \in C_1$
, to define an element of
![]() $\tilde {\Psi }(\tilde {H}_{n,r})$
and deduce that this element agrees with g. Writing the relation
$\tilde {\Psi }(\tilde {H}_{n,r})$
and deduce that this element agrees with g. Writing the relation
![]() $\prod _{a \in \operatorname {{\mathrm {LQ}}}_1} \psi _a=1$
in terms of
$\prod _{a \in \operatorname {{\mathrm {LQ}}}_1} \psi _a=1$
in terms of
![]() $\psi _a$
,
$\psi _a$
,
![]() $a \in C_1$
, we see that
$a \in C_1$
, we see that
 $$\begin{align*}\prod_{i=1}^r \left(\frac{\psi_{a^2_{i}}}{\psi_{a^2_{i-1}}}\right)^r \prod_{i=r+1}^n \psi_{a^2_{i}}^r=1. \end{align*}$$
$$\begin{align*}\prod_{i=1}^r \left(\frac{\psi_{a^2_{i}}}{\psi_{a^2_{i-1}}}\right)^r \prod_{i=r+1}^n \psi_{a^2_{i}}^r=1. \end{align*}$$
So
![]() $(\xi _a((\psi _a)_{a \in C_1}))$
defines an element of
$(\xi _a((\psi _a)_{a \in C_1}))$
defines an element of
![]() $\tilde {\Psi }(\tilde {H}_{n,r}) \subset \tilde {G}$
which agrees with g along
$\tilde {\Psi }(\tilde {H}_{n,r}) \subset \tilde {G}$
which agrees with g along
![]() $a \in C_1$
and satisfies the other two conditions. It follows that
$a \in C_1$
and satisfies the other two conditions. It follows that
![]() $g=\xi ((\psi _a)_{a \in C_1})$
, and in particular
$g=\xi ((\psi _a)_{a \in C_1})$
, and in particular
![]() $g \in \tilde {\Psi }(\tilde {H}_{n,r})$
. Finally, we conclude that
$g \in \tilde {\Psi }(\tilde {H}_{n,r})$
. Finally, we conclude that
![]() $[g] \in \Psi (H_{n,r})$
as claimed.
$[g] \in \Psi (H_{n,r})$
as claimed.
To translate this combinatorial statement to geometry, we extend the G-action from
![]() $X_P$
to the family which gives the toric degeneration. The degeneration is given by the Plücker relations. To illustrate, we describe the
$X_P$
to the family which gives the toric degeneration. The degeneration is given by the Plücker relations. To illustrate, we describe the
![]() $\operatorname {{\mathrm {Gr}}}(5,2)$
example:
$\operatorname {{\mathrm {Gr}}}(5,2)$
example:
Example 4.11. When
![]() $n=5$
,
$n=5$
,
![]() $r=2$
, the family is given by the five polynomials
$r=2$
, the family is given by the five polynomials
that is, this is a family in
![]() $\mathbb {P}^{9} \times {\mathbb {C}}$
, where the coordinate on the second factor is c. The fiber over
$\mathbb {P}^{9} \times {\mathbb {C}}$
, where the coordinate on the second factor is c. The fiber over
![]() $c=0$
is the degenerate toric variety
$c=0$
is the degenerate toric variety
![]() $X_{P_{5,2}}$
, and the generic fiber is isomorphic to the Grassmannian
$X_{P_{5,2}}$
, and the generic fiber is isomorphic to the Grassmannian
![]() $\operatorname {{\mathrm {Gr}}}(5,2)$
. To make this family G-equivariant, we need to extend the action of G to the coefficient c. Label the vertices of the ladder diagram as shown:
$\operatorname {{\mathrm {Gr}}}(5,2)$
. To make this family G-equivariant, we need to extend the action of G to the coefficient c. Label the vertices of the ladder diagram as shown:

There are nine arrows in the ladder quiver, which we label
where
![]() $a_{i,j}$
is an arrow from
$a_{i,j}$
is an arrow from
![]() $i \to j$
, and we add a
$i \to j$
, and we add a
![]() $'$
to the lower arrow if there are two such arrows. Consider the first equation above. The weight of the first monomial is
$'$
to the lower arrow if there are two such arrows. Consider the first equation above. The weight of the first monomial is
![]() $\psi _{a_{0,3}} \psi _{a_{0,2}} \psi _{a_{2,3}}$
; the weight of both the second and third monomial is
$\psi _{a_{0,3}} \psi _{a_{0,2}} \psi _{a_{2,3}}$
; the weight of both the second and third monomial is
![]() $\psi _{a_{0,1}} \psi _{a_{1,3}} \psi _{a_{0,1}'} \psi _{a_{1,2}} \psi _{a_{2,3}}$
, so for c to be equivariant in this equation, it should have weight
$\psi _{a_{0,1}} \psi _{a_{1,3}} \psi _{a_{0,1}'} \psi _{a_{1,2}} \psi _{a_{2,3}}$
, so for c to be equivariant in this equation, it should have weight
However, as we go through the remaining five relations, the required weight for c changes, so we are forced to introduce multiple coefficients. Consider the polynomials
We view the toric degeneration as a family in
![]() $Z\subset \mathbb {P}^{9} \times {\mathbb {C}}^5$
, where the second factor has coordinates
$Z\subset \mathbb {P}^{9} \times {\mathbb {C}}^5$
, where the second factor has coordinates
![]() $(c_i)$
, and the equations cutting out Z are above. Computing the required weights of
$(c_i)$
, and the equations cutting out Z are above. Computing the required weights of
![]() $c_1,\dots ,c_5$
, we note that
$c_1,\dots ,c_5$
, we note that
![]() $c_1$
has the same weight as
$c_1$
has the same weight as
![]() $c_2$
and
$c_2$
and
![]() $c_4$
has the same weight as
$c_4$
has the same weight as
![]() $c_5$
. The variable
$c_5$
. The variable
![]() $c_3$
has the weight of the monomial
$c_3$
has the weight of the monomial
![]() $c_1 c_4$
. To get rid of the excess variables, we add the equations
$c_1 c_4$
. To get rid of the excess variables, we add the equations
Consider the quotient
![]() $Z/G$
. The special fiber—when
$Z/G$
. The special fiber—when
![]() $c_i=0$
—is
$c_i=0$
—is
![]() $X_{P_{n,r}}/G$
. Now, consider a generic fiber of Z. The equation
$X_{P_{n,r}}/G$
. Now, consider a generic fiber of Z. The equation
![]() $c_i=1$
is not homogeneous for the G-action; however, we can consider the disconnected subvariety
$c_i=1$
is not homogeneous for the G-action; however, we can consider the disconnected subvariety
![]() $Z_{1}$
cut out of Z by the equations
$Z_{1}$
cut out of Z by the equations
![]() $c_i^5=1$
,
$c_i^5=1$
,
![]() $i \in \{1,\ldots ,5\}$
. The subgroup of G that preserves a given component of
$i \in \{1,\ldots ,5\}$
. The subgroup of G that preserves a given component of
![]() $Z_{1}$
is precisely
$Z_{1}$
is precisely
![]() $H_{5,2}$
. The number of components of
$H_{5,2}$
. The number of components of
![]() $Z_1$
is 25. The group
$Z_1$
is 25. The group
![]() $G/H_{5,2}$
has order
$G/H_{5,2}$
has order
![]() $25$
. Comparing group sizes, it follows that
$25$
. Comparing group sizes, it follows that
![]() $Z_{1}/G=\operatorname {{\mathrm {Gr}}}(5,2)/H_{5,2}$
.
$Z_{1}/G=\operatorname {{\mathrm {Gr}}}(5,2)/H_{5,2}$
.
The situation is slightly more complicated in the general case. As in the example,
![]() $X_P$
is the special fiber of a family of varieties
$X_P$
is the special fiber of a family of varieties
We denote points in
![]() ${\mathbb {C}}^m$
as
${\mathbb {C}}^m$
as
![]() $\underline {c}$
. The coordinates of
$\underline {c}$
. The coordinates of
![]() $\underline {c}$
give coefficients for all monomials in the Plücker relations that disappear under the degeneration, and
$\underline {c}$
give coefficients for all monomials in the Plücker relations that disappear under the degeneration, and
![]() $\tilde {Z}_{\underline {c}}$
is
$\tilde {Z}_{\underline {c}}$
is
![]() $\tilde {Z} \cap \pi ^{-1}(\underline {c})$
. If
$\tilde {Z} \cap \pi ^{-1}(\underline {c})$
. If
![]() $\underline {c}_1:=(1,\dots ,1)$
and
$\underline {c}_1:=(1,\dots ,1)$
and
![]() $\underline {c}_0:=(0,\dots ,0)$
, then
$\underline {c}_0:=(0,\dots ,0)$
, then
![]() $\tilde {Z}_{\underline {c}_1}=\operatorname {{\mathrm {Gr}}}(n,r)$
and
$\tilde {Z}_{\underline {c}_1}=\operatorname {{\mathrm {Gr}}}(n,r)$
and
![]() $\tilde {Z}_{\underline {c}_0}=X_{P_{n,r}}$
. The generic fiber is isomorphic to
$\tilde {Z}_{\underline {c}_0}=X_{P_{n,r}}$
. The generic fiber is isomorphic to
![]() $\operatorname {{\mathrm {Gr}}}(n,r)$
.
$\operatorname {{\mathrm {Gr}}}(n,r)$
.
We can extend the action of G to
![]() $\mathbb {P}^{\binom {n}{r}-1} \times {\mathbb {C}}^m \to {\mathbb {C}}^m$
by defining the action on
$\mathbb {P}^{\binom {n}{r}-1} \times {\mathbb {C}}^m \to {\mathbb {C}}^m$
by defining the action on
![]() ${\mathbb {C}}^m$
to be the one that ensures
${\mathbb {C}}^m$
to be the one that ensures
![]() $\tilde {Z}$
is preserved by G. Note that
$\tilde {Z}$
is preserved by G. Note that
![]() $G_h$
is the subgroup of G that acts trivially on
$G_h$
is the subgroup of G that acts trivially on
![]() ${\mathbb {C}}^m$
. As in Example 4.11, in general some of these variables are redundant. In fact, the proof of Theorem 4.9 shows that we need only the special
${\mathbb {C}}^m$
. As in Example 4.11, in general some of these variables are redundant. In fact, the proof of Theorem 4.9 shows that we need only the special
![]() $2 \times 2$
three-term Plücker relations associated to each internal vertex in the ladder quiver. More precisely, the proof shows that if
$2 \times 2$
three-term Plücker relations associated to each internal vertex in the ladder quiver. More precisely, the proof shows that if
![]() $g \in G$
preserves these relations, then it in fact preserves all Plücker relations. Let
$g \in G$
preserves these relations, then it in fact preserves all Plücker relations. Let
![]() $d_v$
, where v is an internal vertex, denote the these coefficients. Then for any other coefficient c, the weight of c under the G-action can be expressed as a ratio of the
$d_v$
, where v is an internal vertex, denote the these coefficients. Then for any other coefficient c, the weight of c under the G-action can be expressed as a ratio of the
![]() $d_v$
. Whatever these ratios are, they give a collection of polynomial equations between the
$d_v$
. Whatever these ratios are, they give a collection of polynomial equations between the
![]() $c_i$
, which we call
$c_i$
, which we call
Before we can define the family we want, we need to cut down by one last equation, which is nontrivial when
![]() $\gcd (n,r)>1$
. (It did not occur in our earlier example because
$\gcd (n,r)>1$
. (It did not occur in our earlier example because
![]() $5$
and
$5$
and
![]() $2$
are coprime.) This will be a G-equivariant equation, of course, and will take some time to describe.
$2$
are coprime.) This will be a G-equivariant equation, of course, and will take some time to describe.
Definition 4.12. Fix integers
![]() $n>r>0$
, and set
$n>r>0$
, and set
![]() $k=n-r$
and
$k=n-r$
and
![]() $d=\gcd (n,r)$
. Then there exist s, t such that
$d=\gcd (n,r)$
. Then there exist s, t such that
![]() $r=s d$
and
$r=s d$
and
![]() $k=t d$
. The ladder diagram
$k=t d$
. The ladder diagram
![]() $\operatorname {{\mathrm {LQ}}}_{n,r}$
can be subdivided into an
$\operatorname {{\mathrm {LQ}}}_{n,r}$
can be subdivided into an
![]() $s \times t$
grid of
$s \times t$
grid of
![]() $d \times d$
squares. The set of d-diagonal vertices in
$d \times d$
squares. The set of d-diagonal vertices in
![]() $\operatorname {{\mathrm {LQ}}}_0$
is the set of
$\operatorname {{\mathrm {LQ}}}_0$
is the set of
![]() $v \in \operatorname {{\mathrm {LQ}}}_0$
such that v lies on the diagonal of one of the
$v \in \operatorname {{\mathrm {LQ}}}_0$
such that v lies on the diagonal of one of the
![]() $d \times d$
squares. To a d-diagonal vertex v lying in a
$d \times d$
squares. To a d-diagonal vertex v lying in a
![]() $d \times d$
square B, we associate an incomparable pair of partitions
$d \times d$
square B, we associate an incomparable pair of partitions
![]() $\sigma _{B,v}$
,
$\sigma _{B,v}$
,
![]() $\mu _{B,v}$
. As before, we only specify these partitions locally, insisting that they agree outside of B. The partitions are specified by the statement that their union contains both the vertical and horizontal line (contained in B) passing through the vertex v and that both partitions pass through the bottom-left and top-right vertices of B. We draw the two partitions below.
$\mu _{B,v}$
. As before, we only specify these partitions locally, insisting that they agree outside of B. The partitions are specified by the statement that their union contains both the vertical and horizontal line (contained in B) passing through the vertex v and that both partitions pass through the bottom-left and top-right vertices of B. We draw the two partitions below.

We denote by
![]() $\sigma _B$
and
$\sigma _B$
and
![]() $\mu _B$
the two partitions that agree with
$\mu _B$
the two partitions that agree with
![]() $\sigma _{B,v}$
and
$\sigma _{B,v}$
and
![]() $\mu _{B,v}$
away from B and follow the border of B:
$\mu _{B,v}$
away from B and follow the border of B:

Lemma 4.13. Let v be a d-diagonal vertex in the ladder diagram
![]() $\operatorname {{\mathrm {LQ}}}_{n,r}$
. Then there is a Plücker relation that contains both
$\operatorname {{\mathrm {LQ}}}_{n,r}$
. Then there is a Plücker relation that contains both
![]() $p_{\sigma _B} p_{\mu _B}$
and
$p_{\sigma _B} p_{\mu _B}$
and
![]() $p_{\sigma _{B,v}} p_{\mu _{B,v}}$
.
$p_{\sigma _{B,v}} p_{\mu _{B,v}}$
.
Proof. Suppose that v is the ath d-diagonal vertex in the box B, and suppose that the label on the bottom-left vertical step of B is i. Then
![]() $I(\sigma _{B,v})$
differs from
$I(\sigma _{B,v})$
differs from
![]() $I(\mu _{B,v})$
only in the range
$I(\mu _{B,v})$
only in the range
![]() $M:=\{ j \mid i \leq j \leq i+2d-1\}$
. It is easy to see that
$M:=\{ j \mid i \leq j \leq i+2d-1\}$
. It is easy to see that
and
If
![]() $I(\sigma _{B,v})=\{s_1 < \cdots <s_r\}$
and
$I(\sigma _{B,v})=\{s_1 < \cdots <s_r\}$
and
![]() $I(\mu _{B,v})=\{t_1<\cdots < t_r\}$
, then choose p such that
$I(\mu _{B,v})=\{t_1<\cdots < t_r\}$
, then choose p such that
![]() $s_p=i+a-1$
. So we can obtain
$s_p=i+a-1$
. So we can obtain
![]() $I(\sigma _B)$
and
$I(\sigma _B)$
and
![]() $I(\mu _B)$
from
$I(\mu _B)$
from
![]() $I(\sigma _{B,v})$
and
$I(\sigma _{B,v})$
and
![]() $I(\mu _{B,v})$
by swapping
$I(\mu _{B,v})$
by swapping
![]() $s_{p+1}<\cdots <s_{d-a+p}$
with
$s_{p+1}<\cdots <s_{d-a+p}$
with
![]() $t_{p+1}<\dots <t_{d-a+p}$
. This implies that there is a Plücker relation where both terms appear. For completeness, we construct a relation using [Reference Manivel17, equation 3.1.3] in the case when
$t_{p+1}<\dots <t_{d-a+p}$
. This implies that there is a Plücker relation where both terms appear. For completeness, we construct a relation using [Reference Manivel17, equation 3.1.3] in the case when
![]() $2a \geq d$
and in the case where
$2a \geq d$
and in the case where
![]() $2a<d$
.
$2a<d$
.
In each case, we will identify subsets of indices
![]() $J_s=\{s_{i_1},\dots ,s_{i_l}\}$
and
$J_s=\{s_{i_1},\dots ,s_{i_l}\}$
and
![]() $J_{t}=\{t_{j_1},\dots ,t_{j_{r-l}}\}$
. Let S be the symmetric group permuting the symbols in the union
$J_{t}=\{t_{j_1},\dots ,t_{j_{r-l}}\}$
. Let S be the symmetric group permuting the symbols in the union
![]() $J_s \cup J_t$
, and
$J_s \cup J_t$
, and
![]() $S_1 \times S_2$
the subgroup of S that preserves
$S_1 \times S_2$
the subgroup of S that preserves
![]() $I(\sigma _{B,v})$
and
$I(\sigma _{B,v})$
and
![]() $I(\mu _{B,v})$
. For
$I(\mu _{B,v})$
. For
![]() $\omega \in S/(S_1 \times S_2)$
, set
$\omega \in S/(S_1 \times S_2)$
, set
and
Then for any choice of
![]() $J_s$
and
$J_s$
and
![]() $J_t$
, the following equation is a Plücker relation:
$J_t$
, the following equation is a Plücker relation:
When
![]() $2a \geq d$
, we choose
$2a \geq d$
, we choose
When
![]() $2a < d$
, we choose
$2a < d$
, we choose
Note that for each choice the terms
![]() $p_{\sigma _{B,v}} p_{\mu _{B,v}}$
and
$p_{\sigma _{B,v}} p_{\mu _{B,v}}$
and
![]() $p_{\sigma _{B}} p_{\mu _{B}}$
appear with nonzero coefficient as claimed.
$p_{\sigma _{B}} p_{\mu _{B}}$
appear with nonzero coefficient as claimed.
From the proof of Theorem 4.9, the weight of the ratio
![]() $p_{\sigma _{B,v}} p_{\mu _{B,v}}/(p_{\sigma _{B}} p_{\mu _{B}})$
can be expressed as a ratio of the weights of
$p_{\sigma _{B,v}} p_{\mu _{B,v}}/(p_{\sigma _{B}} p_{\mu _{B}})$
can be expressed as a ratio of the weights of
![]() $d_w$
, where w ranges over the internal vertices. Let
$d_w$
, where w ranges over the internal vertices. Let
![]() $f_{B,v}(d_w)$
be this ratio.
$f_{B,v}(d_w)$
be this ratio.
Lemma 4.14. The group G acts trivially on the product
![]() $(\prod _{(B,v)} f_{B,v})^{\frac {n}{d}}$
, where
$(\prod _{(B,v)} f_{B,v})^{\frac {n}{d}}$
, where
![]() $(B,v)$
ranges over internal diagonal vertices in the
$(B,v)$
ranges over internal diagonal vertices in the
![]() $d \times d$
boxes B of the ladder diagram.
$d \times d$
boxes B of the ladder diagram.
Proof. When
![]() $d=1$
, the statement is trivial. To prove the lemma, we will show that the weight of
$d=1$
, the statement is trivial. To prove the lemma, we will show that the weight of
![]() $\prod _{(B,v)} f_{B,v}$
is an order
$\prod _{(B,v)} f_{B,v}$
is an order
![]() $n/d$
element of G. We will describe this element precisely. Let
$n/d$
element of G. We will describe this element precisely. Let
![]() $r=sd$
and
$r=sd$
and
![]() $n-r=td$
. We have divided the ladder diagram into a
$n-r=td$
. We have divided the ladder diagram into a
![]() $s \times t$
grid of
$s \times t$
grid of
![]() $d\times d$
boxes. Consider the collection C of arrows entirely contained in the border of the
$d\times d$
boxes. Consider the collection C of arrows entirely contained in the border of the
![]() $d \times d$
boxes. Then we will show that the weight of
$d \times d$
boxes. Then we will show that the weight of
![]() $\prod _{(B,v)} f_{B,v}$
is
$\prod _{(B,v)} f_{B,v}$
is
This is an order
![]() $n/d$
element of G as desired. The easiest way to see that this weight is correct is to visualize the weights using paths in the ladder diagram. We will indicate a weight by drawing paths in the ladder diagram, possibly in reverse, and allowing multiple arrows. Each arrow appearing contributes a weight of
$n/d$
element of G as desired. The easiest way to see that this weight is correct is to visualize the weights using paths in the ladder diagram. We will indicate a weight by drawing paths in the ladder diagram, possibly in reverse, and allowing multiple arrows. Each arrow appearing contributes a weight of
![]() $\zeta _a^{b^+-b^-}$
, where
$\zeta _a^{b^+-b^-}$
, where
![]() $b^+$
is the number of times a appears in the correct direction and
$b^+$
is the number of times a appears in the correct direction and
![]() $b^-$
is the number of times it appears in the reverse direction. For example, the weight of
$b^-$
is the number of times it appears in the reverse direction. For example, the weight of
![]() $f_{B,v}$
is pictured as
$f_{B,v}$
is pictured as

Now, consider the weight of the product of
![]() $f_{B,v}$
where B is fixed:
$f_{B,v}$
where B is fixed:
![]() $\prod _{v} f_{B,v}$
. Pictorially, this corresponds to overlaying the diagrams for each of internal vertices v. Note that the arrows going in a positive direction have no intersection except on the border, and every such arrow is covered exactly once. Depending on where B is located in the ladder diagram, there could be vertices along the borders of B or not, which changes how many times each arrow appears. If there are no vertices on a particular edge, then there are
$\prod _{v} f_{B,v}$
. Pictorially, this corresponds to overlaying the diagrams for each of internal vertices v. Note that the arrows going in a positive direction have no intersection except on the border, and every such arrow is covered exactly once. Depending on where B is located in the ladder diagram, there could be vertices along the borders of B or not, which changes how many times each arrow appears. If there are no vertices on a particular edge, then there are
![]() $d-1$
arrows in the reverse direction along that edge (one for each internal vertex). If there are border vertices, then the number of arrows follows a pattern as below (where
$d-1$
arrows in the reverse direction along that edge (one for each internal vertex). If there are border vertices, then the number of arrows follows a pattern as below (where
![]() $-k$
indicates k arrows in the reverse direction of the arrow directly below the label):
$-k$
indicates k arrows in the reverse direction of the arrow directly below the label):

The weight of the product over all boxes B—that is, the weight of
![]() $\prod _{(B,v)} f_{B,v}$
—is read off by combining all of the
$\prod _{(B,v)} f_{B,v}$
—is read off by combining all of the
![]() $d \times d$
boxes to cover the ladder diagram. It is immediate from the above diagram that this gives us the weight
$d \times d$
boxes to cover the ladder diagram. It is immediate from the above diagram that this gives us the weight
Since
![]() $\prod _{a} \zeta _a=1$
, this shows that the weight is equation (14) as desired.
$\prod _{a} \zeta _a=1$
, this shows that the weight is equation (14) as desired.
The lemma states that the action of G on
![]() $(\prod _{(B,v)} f_{B,v})^{\frac {n}{d}}$
is trivial, so the equation
$(\prod _{(B,v)} f_{B,v})^{\frac {n}{d}}$
is trivial, so the equation
![]() $(\prod _{(B,v)} f_{B,v})^{\frac {n}{d}}=1$
is homogeneous. If we wish, since the left-hand side is a monomial, we can clear the denominator to get a polynomial equation. We call the set containing this single polynomial equation
$(\prod _{(B,v)} f_{B,v})^{\frac {n}{d}}=1$
is homogeneous. If we wish, since the left-hand side is a monomial, we can clear the denominator to get a polynomial equation. We call the set containing this single polynomial equation
This is the last equation we need to define our family.
Definition 4.15. Let
![]() $Z \subset \mathbb {P}^{\binom {n}{r}-1} \times B \xrightarrow {\pi } B$
denote the family cut out by the following three types of the equations:
$Z \subset \mathbb {P}^{\binom {n}{r}-1} \times B \xrightarrow {\pi } B$
denote the family cut out by the following three types of the equations:
-
1. the Plücker relations,
-
2. the polynomial equations
 $\mathcal {P}_1$
from equation (13),
$\mathcal {P}_1$
from equation (13), -
3. the polynomial equation
 $\mathcal {P}_2$
from equation (15).
$\mathcal {P}_2$
from equation (15).
The last two equations cut out
![]() $B \subset {\mathbb {C}}^m$
.
$B \subset {\mathbb {C}}^m$
.
By construction, Z is a G-invariant algebraic variety. We use notation as for the family
![]() $\tilde {Z}$
in equation (12). Note that the fiber
$\tilde {Z}$
in equation (12). Note that the fiber
![]() $Z_{\underline {c}_0}$
is invariant under the G action, but
$Z_{\underline {c}_0}$
is invariant under the G action, but
![]() $Z_{\underline {c}_1}$
is not. However, since the action of G on on
$Z_{\underline {c}_1}$
is not. However, since the action of G on on
![]() ${\mathbb {C}}^m$
is of order n, the disconnected variety
${\mathbb {C}}^m$
is of order n, the disconnected variety
![]() $\hat {Z}_{\underline {b}}:=Z \cap \pi ^{-1}(\{(c_1,\dots ,c_m) \in B: c_i^n=b_i\})$
is G-invariant for any
$\hat {Z}_{\underline {b}}:=Z \cap \pi ^{-1}(\{(c_1,\dots ,c_m) \in B: c_i^n=b_i\})$
is G-invariant for any
![]() $\underline {b} \in {\mathbb {C}}^m$
. We will consider the quotient family
$\underline {b} \in {\mathbb {C}}^m$
. We will consider the quotient family
![]() $Z/G \to B/G$
.
$Z/G \to B/G$
.
The next result gives the precise sense in which
![]() $\operatorname {{\mathrm {Gr}}}(n,r)/H_{n,r}$
is a smoothing of
$\operatorname {{\mathrm {Gr}}}(n,r)/H_{n,r}$
is a smoothing of
![]() $X_{P_{n,r}}/G$
.
$X_{P_{n,r}}/G$
.
Theorem 4.16. Suppose b is generic (i.e.,
![]() $b_i \neq 0$
for all i). Then
$b_i \neq 0$
for all i). Then
![]() $\hat {Z}_{\underline {b}}/G$
is a fiber of the quotient family
$\hat {Z}_{\underline {b}}/G$
is a fiber of the quotient family
![]() $Z/G \to B/G$
, and
$Z/G \to B/G$
, and
![]() $\hat {Z}_{\underline {b}}/G \cong \operatorname {{\mathrm {Gr}}}(n,r)/H_{n,r}$
.
$\hat {Z}_{\underline {b}}/G \cong \operatorname {{\mathrm {Gr}}}(n,r)/H_{n,r}$
.
Proof. For simplicity, we will set
![]() $b_i=1$
for all i and denote
$b_i=1$
for all i and denote
![]() $\hat {Z}_{\underline {b}}/G$
by
$\hat {Z}_{\underline {b}}/G$
by
![]() $\hat {Z}_1/G$
. The variety
$\hat {Z}_1/G$
. The variety
![]() $\hat {Z}_1$
is disconnected, with components we can label
$\hat {Z}_1$
is disconnected, with components we can label
![]() $A_1 \sqcup \cdots \sqcup A_s$
. One component, which we label
$A_1 \sqcup \cdots \sqcup A_s$
. One component, which we label
![]() $A_1$
, is the Grassmannian
$A_1$
, is the Grassmannian
![]() $\operatorname {{\mathrm {Gr}}}(n,r)$
. The quotient can be studied in two steps:
$\operatorname {{\mathrm {Gr}}}(n,r)$
. The quotient can be studied in two steps:
Note that the stabilizer of any element of
![]() $\bigsqcup A_i/G_h$
under the
$\bigsqcup A_i/G_h$
under the
![]() $G/G_h$
-action is trivial, as only
$G/G_h$
-action is trivial, as only
![]() $G_h$
preserves the components. Thus, the size of an orbit of a point in
$G_h$
preserves the components. Thus, the size of an orbit of a point in
![]() $\bigsqcup A_i/G_h$
is
$\bigsqcup A_i/G_h$
is
In particular, the number of components s is at least
![]() $n^{(r-1)(n-r-1)-1} n/d$
. On first glance, it may appear that
$n^{(r-1)(n-r-1)-1} n/d$
. On first glance, it may appear that
![]() $\hat {Z}_1$
has
$\hat {Z}_1$
has
![]() $n^m$
components, but in fact, the equations from
$n^m$
components, but in fact, the equations from
![]() $\mathcal {P}_1$
and
$\mathcal {P}_1$
and
![]() $\mathcal {P}_2$
cut this down considerably. The equations from
$\mathcal {P}_2$
cut this down considerably. The equations from
![]() $\mathcal {P}_1$
mean that we can regard all coefficients
$\mathcal {P}_1$
mean that we can regard all coefficients
![]() $c_i$
as a function of the coefficients
$c_i$
as a function of the coefficients
![]() $d_v$
, where v is an internal vertex of the ladder quiver, so there are at most
$d_v$
, where v is an internal vertex of the ladder quiver, so there are at most
![]() $n^{(r-1)(n-r-1)}$
components. The single equation in
$n^{(r-1)(n-r-1)}$
components. The single equation in
![]() $\mathcal {P}_2$
is of the form
$\mathcal {P}_2$
is of the form
![]() $f^{n/d},$
which means that in fact the largest possible number of components is
$f^{n/d},$
which means that in fact the largest possible number of components is
![]() $n^{(r-1)(n-r-1)-1} n/d$
. So
$n^{(r-1)(n-r-1)-1} n/d$
. So
This means that the residual
![]() $G/G_h$
action identifies each of the components
$G/G_h$
action identifies each of the components
![]() $A_i/G_h$
, so
$A_i/G_h$
, so
This also shows that the orbit of a point in the base of the family Z is precisely the set
![]() $\{(c_1,\dots ,c_m) \in B: c_i^n=b_i\}$
.
$\{(c_1,\dots ,c_m) \in B: c_i^n=b_i\}$
.
4.2 Smoothing
 $Y_{n,r}$
and
$Y_{n,r}$
and
 $Y_{n,r}/G$
$Y_{n,r}/G$
Recall from Theorem 3.7 that there is a toric variety
![]() $Y_{n,r}$
characterized as a blow-up of
$Y_{n,r}$
characterized as a blow-up of
![]() $X_{P_{n,r}}$
obtained by adding the rays required to take
$X_{P_{n,r}}$
obtained by adding the rays required to take
![]() $P_{n,r}$
to
$P_{n,r}$
to
![]() $Q_{n,r}$
. The variety
$Q_{n,r}$
. The variety
![]() $Y_{n,r}$
is of interest as it fits into the following diagrams:
$Y_{n,r}$
is of interest as it fits into the following diagrams:

![]() $Y_{n,r}$
is the toric variety associated to the fan obtained from the spanning fan of
$Y_{n,r}$
is the toric variety associated to the fan obtained from the spanning fan of
![]() $P_{n,r}$
by blowing up at the rays
$P_{n,r}$
by blowing up at the rays
![]() $v_{\lambda } \in N$
, for
$v_{\lambda } \in N$
, for
![]() $\lambda \in {\mathcal {B}(n,r)}$
a redundant partition. This depends on the order in which the blow-up is completed.
$\lambda \in {\mathcal {B}(n,r)}$
a redundant partition. This depends on the order in which the blow-up is completed.
Each
![]() $v_{\lambda }$
lies in the interior of an intersection of maximal cones of the spanning fan of
$v_{\lambda }$
lies in the interior of an intersection of maximal cones of the spanning fan of
![]() $P_{n,r}$
. Maximal cones of this fan are also indexed by partitions, but not just those in
$P_{n,r}$
. Maximal cones of this fan are also indexed by partitions, but not just those in
![]() ${\mathcal {B}(n,r)}$
: There is a maximal cone
${\mathcal {B}(n,r)}$
: There is a maximal cone
![]() $C_{\mu }$
for each
$C_{\mu }$
for each
![]() $\mu \in {\mathcal {P}(n,r)}$
corresponding to the section of
$\mu \in {\mathcal {P}(n,r)}$
corresponding to the section of
![]() $\mathcal {O}(1)$
indexed by
$\mathcal {O}(1)$
indexed by
![]() $\mu $
.
$\mu $
.
Definition 4.17. For each
![]() $\lambda \in {\mathcal {B}(n,r)}$
, let
$\lambda \in {\mathcal {B}(n,r)}$
, let
![]() $\operatorname {{\mathrm {Cones}}}(\lambda ):=\{\mu \in {\mathcal {P}(n,r)}: v_{\lambda } \in C_{\mu }\},$
the collection of all maximal cones of the spanning fan of
$\operatorname {{\mathrm {Cones}}}(\lambda ):=\{\mu \in {\mathcal {P}(n,r)}: v_{\lambda } \in C_{\mu }\},$
the collection of all maximal cones of the spanning fan of
![]() $P_{n,r}$
that contain
$P_{n,r}$
that contain
![]() $v_{\lambda }$
. Fix an order on
$v_{\lambda }$
. Fix an order on
![]() ${\mathcal {B}(n,r)}$
. Let
${\mathcal {B}(n,r)}$
. Let
![]() $\operatorname {{\mathrm {Bl}}} \mathbb {P}$
denote the iterated blow-up of
$\operatorname {{\mathrm {Bl}}} \mathbb {P}$
denote the iterated blow-up of
![]() $\mathbb {P}^{\binom {n}{r}-1}$
at the linear subspaces
$\mathbb {P}^{\binom {n}{r}-1}$
at the linear subspaces
where we iterate over
![]() $\lambda \in {\mathcal {B}(n,r)}$
. We define
$\lambda \in {\mathcal {B}(n,r)}$
. We define
![]() $\operatorname {{\mathrm {Bl}}} \operatorname {{\mathrm {Gr}}}(n,r)$
to be the iterated blow-up of
$\operatorname {{\mathrm {Bl}}} \operatorname {{\mathrm {Gr}}}(n,r)$
to be the iterated blow-up of
![]() $\operatorname {{\mathrm {Gr}}}(n,r)$
at these same subspaces.
$\operatorname {{\mathrm {Gr}}}(n,r)$
at these same subspaces.
Consider the Cox ring of of
![]() $\operatorname {{\mathrm {Bl}}} \mathbb {P}$
. In addition to the
$\operatorname {{\mathrm {Bl}}} \mathbb {P}$
. In addition to the
![]() $p_{\mu }$
,
$p_{\mu }$
,
![]() $\mu \in {\mathcal {P}(n,r)}$
, there is a generator
$\mu \in {\mathcal {P}(n,r)}$
, there is a generator
![]() $x_{\lambda }$
for each
$x_{\lambda }$
for each
![]() $\lambda \in {\mathcal {B}(n,r)}$
graded by the Cartier divisor corresponding to the ray added when blowing up at the
$\lambda \in {\mathcal {B}(n,r)}$
graded by the Cartier divisor corresponding to the ray added when blowing up at the
![]() $\lambda $
th step. Now, instead of blowing up
$\lambda $
th step. Now, instead of blowing up
![]() $X_{P_{n,r}}$
using toric geometry, we can view it as a subvariety of
$X_{P_{n,r}}$
using toric geometry, we can view it as a subvariety of
![]() $\mathbb {P}^{\binom {n}{r}-1}$
, then compute the blow-up of
$\mathbb {P}^{\binom {n}{r}-1}$
, then compute the blow-up of
![]() $X_{P_{n,r}}$
as the main component of its proper transform in the ambient blow-up.
$X_{P_{n,r}}$
as the main component of its proper transform in the ambient blow-up.
To write down the binomial equations, we adjust the binomial equations cutting
![]() $X_{P_{n,r}}$
out of
$X_{P_{n,r}}$
out of
![]() $\mathbb {P}^{\binom {n}{r}-1}$
. Let
$\mathbb {P}^{\binom {n}{r}-1}$
. Let
![]() $\sigma _1$
and
$\sigma _1$
and
![]() $\sigma _2$
be an incomparable pair, giving rise to the binomial equation
$\sigma _2$
be an incomparable pair, giving rise to the binomial equation
Although this homogeneous for
![]() $\mathbb {P}^{\binom {n}{r}-1}$
, it is not when considered as an equation in the Cox ring of
$\mathbb {P}^{\binom {n}{r}-1}$
, it is not when considered as an equation in the Cox ring of
![]() $\operatorname {{\mathrm {Bl}}} \mathbb {P}$
. However, there is a natural minimal way to homogenize this equation by multiplying each factor by some combination of generators
$\operatorname {{\mathrm {Bl}}} \mathbb {P}$
. However, there is a natural minimal way to homogenize this equation by multiplying each factor by some combination of generators
![]() $x_{\lambda }$
,
$x_{\lambda }$
,
![]() $\lambda \in {\mathcal {B}(n,r)}$
. Call the subvariety cut out of
$\lambda \in {\mathcal {B}(n,r)}$
. Call the subvariety cut out of
![]() $\operatorname {{\mathrm {Bl}}} \mathbb {P}$
by these adjusted equations
$\operatorname {{\mathrm {Bl}}} \mathbb {P}$
by these adjusted equations
![]() $\operatorname {{\mathrm {Bl}}} X_{P_{n,r}}$
.
$\operatorname {{\mathrm {Bl}}} X_{P_{n,r}}$
.
Lemma 4.18. The subvariety
![]() $\operatorname {{\mathrm {Bl}}} X_{P_{n,r}}$
is the image of
$\operatorname {{\mathrm {Bl}}} X_{P_{n,r}}$
is the image of
![]() $Y_{n,r}$
under the natural embedding
$Y_{n,r}$
under the natural embedding
![]() $Y_{n,r} \to \operatorname {{\mathrm {Bl}}} \mathbb {P}$
.
$Y_{n,r} \to \operatorname {{\mathrm {Bl}}} \mathbb {P}$
.
Note that we can lift the action of G on
![]() $\operatorname {{\mathrm {Gr}}}(n,r)$
and
$\operatorname {{\mathrm {Gr}}}(n,r)$
and
![]() $X_{P_{n,r}}$
to their blow-ups.
$X_{P_{n,r}}$
to their blow-ups.
Theorem 4.19. There is a degeneration of
![]() $\operatorname {{\mathrm {Bl}}} \operatorname {{\mathrm {Gr}}}(n,r)$
to a possibly disconnected variety whose main component is
$\operatorname {{\mathrm {Bl}}} \operatorname {{\mathrm {Gr}}}(n,r)$
to a possibly disconnected variety whose main component is
![]() $Y_{n,r}$
. There is a degeneration of
$Y_{n,r}$
. There is a degeneration of
![]() $\operatorname {{\mathrm {Bl}}} \operatorname {{\mathrm {Gr}}}(n,r)/H_{n,r}$
to a possibly disconnected variety whose main component is
$\operatorname {{\mathrm {Bl}}} \operatorname {{\mathrm {Gr}}}(n,r)/H_{n,r}$
to a possibly disconnected variety whose main component is
![]() $Y_{n,r}/G$
.
$Y_{n,r}/G$
.
Proof. The process of homogenization can also be applied to
![]() $\operatorname {{\mathrm {Gr}}}(n,r)$
viewed as a subvariety of
$\operatorname {{\mathrm {Gr}}}(n,r)$
viewed as a subvariety of
![]() $\mathbb {P}^{\binom {n}{r}-1}$
under the Plücker embedding. We can degenerate the homogenized Plücker equations to binomials just as in the Gelfand–Cetlin degeneration: These are the homogenized degenerate Plücker relations cutting out
$\mathbb {P}^{\binom {n}{r}-1}$
under the Plücker embedding. We can degenerate the homogenized Plücker equations to binomials just as in the Gelfand–Cetlin degeneration: These are the homogenized degenerate Plücker relations cutting out
![]() $Y_{n,r}$
, except possibly with extra factors
$Y_{n,r}$
, except possibly with extra factors
![]() $x_{\lambda }$
. This proves the first statement. The proof of the second statement is the same as that of Theorem 4.16, as G acts trivially on the
$x_{\lambda }$
. This proves the first statement. The proof of the second statement is the same as that of Theorem 4.16, as G acts trivially on the
![]() $x_{\lambda }$
,
$x_{\lambda }$
,
![]() $\lambda \in {\mathcal {B}(n,r)}$
.
$\lambda \in {\mathcal {B}(n,r)}$
.
5 A compactification of the Eguchi–Hori–Xiong superpotential
In the final section, we give a tentative proposal for a Calabi–Yau mirror to the Fermat Calabi–Yau hypersurface in the Grassmannian. Eguchi–Hori–Xiong constructed a Laurent polynomial that is a mirror partner to the Grassmannian
![]() $\operatorname {{\mathrm {Gr}}}(n,r)$
[Reference Eguchi, Hori and Xiong9]. It is essentially the toric Hori–Vafa mirror of
$\operatorname {{\mathrm {Gr}}}(n,r)$
[Reference Eguchi, Hori and Xiong9]. It is essentially the toric Hori–Vafa mirror of
![]() $X_{P_{n,r}}$
. If
$X_{P_{n,r}}$
. If
![]() $y_a$
,
$y_a$
,
![]() $a \in \operatorname {{\mathrm {LQ}}}_1$
, are Cox coordinates on
$a \in \operatorname {{\mathrm {LQ}}}_1$
, are Cox coordinates on
![]() $X_{P_{n,r}}$
, then the EHX mirror is
$X_{P_{n,r}}$
, then the EHX mirror is
where
![]() $q=(q_1,\dots ,q_{|\overline {\operatorname {{\mathrm {LQ}}}_0}|})$
are coordinates on the base of the family
$q=(q_1,\dots ,q_{|\overline {\operatorname {{\mathrm {LQ}}}_0}|})$
are coordinates on the base of the family
![]() $\pi :({\mathbb {C}}^*)^{|\operatorname {{\mathrm {LQ}}}_1|} \to ({\mathbb {C}}^*)^{|\overline {\operatorname {{\mathrm {LQ}}}_0}|}$
. By the fiber of W we mean
$\pi :({\mathbb {C}}^*)^{|\operatorname {{\mathrm {LQ}}}_1|} \to ({\mathbb {C}}^*)^{|\overline {\operatorname {{\mathrm {LQ}}}_0}|}$
. By the fiber of W we mean
![]() $W_q^{-1}(c)$
for some c and q.
$W_q^{-1}(c)$
for some c and q.
Marsh–Rietsch [Reference Marsh and Rietsch18] have shown that the classical period of W, after setting
![]() $q_i = 1$
for all i, equals the regularized quantum period of the Grassmannian; for definitions here, see [Reference Coates, Corti, Galkin, Golyshev and Kasprzyk5]. This implies that it is a very weak mirror of the Grassmannian in the sense of [Reference Przyjalkowski20]. There are stronger notions of mirror symmetry. One important one is the following, due to Przyjalkowski [Reference Przyjalkowski20]:
$q_i = 1$
for all i, equals the regularized quantum period of the Grassmannian; for definitions here, see [Reference Coates, Corti, Galkin, Golyshev and Kasprzyk5]. This implies that it is a very weak mirror of the Grassmannian in the sense of [Reference Przyjalkowski20]. There are stronger notions of mirror symmetry. One important one is the following, due to Przyjalkowski [Reference Przyjalkowski20]:
Definition 5.1. Let
![]() $f: ({\mathbb {C}}^*)^n \to {\mathbb {C}}$
be a Laurent polynomial which is a very weak mirror of a Fano variety X. Then f is a weak mirror if the fibers of f can be compactified to Calabi–Yau varieties
$f: ({\mathbb {C}}^*)^n \to {\mathbb {C}}$
be a Laurent polynomial which is a very weak mirror of a Fano variety X. Then f is a weak mirror if the fibers of f can be compactified to Calabi–Yau varieties
![]() $Z^{\vee }$
.
$Z^{\vee }$
.
It is expected that if Z is an anticanonical Calabi–Yau hypersurface in X, then
![]() $(Z,Z^{\vee })$
form a Calabi–Yau mirror pair. This is how Fano and Calabi–Yau mirror symmetry are related when X is a toric variety.
$(Z,Z^{\vee })$
form a Calabi–Yau mirror pair. This is how Fano and Calabi–Yau mirror symmetry are related when X is a toric variety.
For our proposed mirror of the Fermat Calabi–Yau hypersurface in the Grassmannian, we do not check mirror equality of Hodge numbers (given the group action and the blow-up, the computation of Hodge numbers did not seem straightforward to the authors). However, we show that our mirror is a compactification and smoothing of the EHX superpotential, as one would expect.
Definition 5.2. Fix n and r, and let
![]() $\lambda \in {\mathcal {P}(n,r)}$
be a partition. We say that
$\lambda \in {\mathcal {P}(n,r)}$
be a partition. We say that
![]() $\lambda $
is a maximal rectangle if it is rectangular and either maximally wide or maximally tall.
$\lambda $
is a maximal rectangle if it is rectangular and either maximally wide or maximally tall.
Remark 5.3. The variables
![]() $p_{\lambda }$
, where
$p_{\lambda }$
, where
![]() $\lambda $
is maximal rectangular, are the frozen variables for the cluster algebra of the Grassmannian (they appear in every cluster chart).
$\lambda $
is maximal rectangular, are the frozen variables for the cluster algebra of the Grassmannian (they appear in every cluster chart).
Let
![]() $Z_{n,r}^{\vee }$
be the family of hypersurfaces cut out of
$Z_{n,r}^{\vee }$
be the family of hypersurfaces cut out of
![]() $\operatorname {{\mathrm {Bl}}} \operatorname {{\mathrm {Gr}}}(n,r)/H_{n,r}$
by the equation
$\operatorname {{\mathrm {Bl}}} \operatorname {{\mathrm {Gr}}}(n,r)/H_{n,r}$
by the equation
 $$ \begin{align} \sum_{\lambda \in {\mathcal{A}(n,r)}} p_{\lambda}^n + \psi \prod_{p_{\mu} \text{ frozen}} p_{\mu}=0. \end{align} $$
$$ \begin{align} \sum_{\lambda \in {\mathcal{A}(n,r)}} p_{\lambda}^n + \psi \prod_{p_{\mu} \text{ frozen}} p_{\mu}=0. \end{align} $$
Note that this a
![]() $H_{n,r}$
-equivariant equation, so
$H_{n,r}$
-equivariant equation, so
![]() $Z_{n,r}^{\vee }$
is well-defined.
$Z_{n,r}^{\vee }$
is well-defined.
Theorem 5.4.
![]() $Z_{n,r}$
has trivial anticanonical class, so is Calabi–Yau in this sense. It is a compactification of the fibers of the Eguchi–Hori–Xiong mirror.
$Z_{n,r}$
has trivial anticanonical class, so is Calabi–Yau in this sense. It is a compactification of the fibers of the Eguchi–Hori–Xiong mirror.
Proof. We will first show the second part of the statement, and then that equation (16) is a section of the anticanonical line bundle. The adjunction formula then implies that the anticanonical class of the hypersurface is trivial. Let
![]() $A_P$
denote the
$A_P$
denote the
![]() $r(n-r) \times |\operatorname {{\mathrm {LQ}}}_1|$
matrix with integer entries whose columns are given by the rays of the spanning fan of
$r(n-r) \times |\operatorname {{\mathrm {LQ}}}_1|$
matrix with integer entries whose columns are given by the rays of the spanning fan of
![]() ${P_{n,r}}$
written in the basis
${P_{n,r}}$
written in the basis
![]() $\{b_v\}$
. Let
$\{b_v\}$
. Let
![]() $A_{P^{\vee }}$
denote the
$A_{P^{\vee }}$
denote the
![]() $r(n-r) \times \binom {n}{r}$
matrix with integer entries whose columns are given by the rays of the spanning fan of
$r(n-r) \times \binom {n}{r}$
matrix with integer entries whose columns are given by the rays of the spanning fan of
![]() $P_{n,r}^{\vee }$
written in the basis
$P_{n,r}^{\vee }$
written in the basis
![]() $\{b_v^{\vee }\}$
. The
$\{b_v^{\vee }\}$
. The
![]() $|\operatorname {{\mathrm {LQ}}}_1| \times \binom {n}{r}$
matrix
$|\operatorname {{\mathrm {LQ}}}_1| \times \binom {n}{r}$
matrix
defines a map
by exponentiating.
This descends to a map between the dense tori in
![]() $X_{P_{n,r}}$
and
$X_{P_{n,r}}$
and
![]() $X_{P_{n,r}^{\vee }}$
. If we write coordinates on the former as
$X_{P_{n,r}^{\vee }}$
. If we write coordinates on the former as
![]() $y_a$
,
$y_a$
,
![]() $a \in \operatorname {{\mathrm {LQ}}}_1$
, and coordinates on the latter as
$a \in \operatorname {{\mathrm {LQ}}}_1$
, and coordinates on the latter as
![]() $z_{\lambda }$
,
$z_{\lambda }$
,
![]() $\lambda \in {\mathcal {P}(n,r)}$
, then this map is
$\lambda \in {\mathcal {P}(n,r)}$
, then this map is
 $$\begin{align*}(z_{\lambda})_{\lambda \in {\mathcal{P}(n,r)}} \mapsto \left(\frac{\prod_{a \in \mu }z_{\mu}^n}{\prod_{\mu\in {\mathcal{P}(n,r)} }z_{\mu}}\right)_{a \in \operatorname{{\mathrm{LQ}}}_1}. \end{align*}$$
$$\begin{align*}(z_{\lambda})_{\lambda \in {\mathcal{P}(n,r)}} \mapsto \left(\frac{\prod_{a \in \mu }z_{\mu}^n}{\prod_{\mu\in {\mathcal{P}(n,r)} }z_{\mu}}\right)_{a \in \operatorname{{\mathrm{LQ}}}_1}. \end{align*}$$
This takes the locus
![]() $W=-\psi $
to the locus
$W=-\psi $
to the locus
 $$\begin{align*}\sum_{a \in \operatorname{{\mathrm{LQ}}}_1} \prod_{a \in \mu }z_{\mu}^n+\psi \prod_{\mu\in {\mathcal{P}(n,r)} }z_{\mu}=0,\end{align*}$$
$$\begin{align*}\sum_{a \in \operatorname{{\mathrm{LQ}}}_1} \prod_{a \in \mu }z_{\mu}^n+\psi \prod_{\mu\in {\mathcal{P}(n,r)} }z_{\mu}=0,\end{align*}$$
which is a Calabi–Yau hypersurface in
![]() $X_{P_{n,r}^{\vee }}=X_{Q_{n,r}}/G$
. Note that this equation is G-invariant.
$X_{P_{n,r}^{\vee }}=X_{Q_{n,r}}/G$
. Note that this equation is G-invariant.
We now apply Theorem 3.7 and obtain a Calabi–Yau hypersurface in
![]() $Y_{n,r}/G$
. Viewing
$Y_{n,r}/G$
. Viewing
![]() $Y_{n,r}$
as a subvariety of
$Y_{n,r}$
as a subvariety of
![]() $\operatorname {{\mathrm {Bl}}} \mathbb {P}$
, we can choose an identification of Cox rings so that this hypersurface is cut out by the equation
$\operatorname {{\mathrm {Bl}}} \mathbb {P}$
, we can choose an identification of Cox rings so that this hypersurface is cut out by the equation
 $$\begin{align*}\sum_{\lambda \in {\mathcal{A}(n,r)}} p_{\lambda}^n+\psi \prod_{\mu \text{ frozen}}p_{\mu}=0. \end{align*}$$
$$\begin{align*}\sum_{\lambda \in {\mathcal{A}(n,r)}} p_{\lambda}^n+\psi \prod_{\mu \text{ frozen}}p_{\mu}=0. \end{align*}$$
It remains Calabi–Yau even as we deform the equations cutting out
![]() $Y_{n,r}$
, so we get a Calabi–Yau hypersurface in
$Y_{n,r}$
, so we get a Calabi–Yau hypersurface in
![]() $\operatorname {{\mathrm {Bl}}} \operatorname {{\mathrm {Gr}}}(n,r)/H_{n,r}$
.
$\operatorname {{\mathrm {Bl}}} \operatorname {{\mathrm {Gr}}}(n,r)/H_{n,r}$
.
Acknowledgments
The second and third authors thank the Center Of Mathematical Sciences And Applications at Harvard University, where the project started.
Conflict of Interest
The authors have no conflict of interest to declare.
Data availability statement
There are no data associated with this submission.
Ethical standards
The research meets all ethical guidelines.
Funding statement
Tom Coates was supported by ERC Consolidator Grant 682603 and EPSRC Programme Grant EP/N03189X/1. Charles Doran and Elana Kalashnikov were supported by NSERC Discovery grants.
Supplementary material
There is no supplementary material associated with this submission.