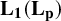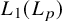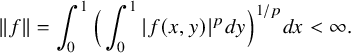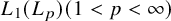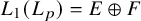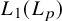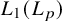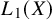1 Introduction
The decomposition of normed linear spaces into direct sums and the analysis of the associated projection operators is central to important chapters in the theory of modern and classical Banach spaces. In a seminal paper, Lindenstrauss [Reference Lindenstrauss23] set forth an influential research program aiming at detailed investigations of complemented subspaces and operators on Banach spaces.
The main question addressed by Lindenstrauss was this: Which are the spaces X that cannot be further decomposed into two `essentially different, infinite-dimensional subspaces'? That is to say, which are the Banach spaces X that are not isomorphic to the direct sum of two infinite-dimensional spaces Y and Z, where neither Y nor Z is isomorphic to X? This condition would be satisfied if X were indecomposable: that is, for any decomposition of X into two spaces, one of them has to be finite-dimensional. Separately, such a space could be primary, meaning that for any decomposition of X into two spaces, one of them has to be isomorphic to
![]() $X.$
The first example of an indecomposable Banach space was constructed by Gowers and Maurey [Reference Gowers and Maurey18], who also showed that their space
$X.$
The first example of an indecomposable Banach space was constructed by Gowers and Maurey [Reference Gowers and Maurey18], who also showed that their space
![]() $X_{\mathrm {GM}} $
is not primary – the infinite-dimensional component of
$X_{\mathrm {GM}} $
is not primary – the infinite-dimensional component of
![]() $X_{\mathrm {GM}} \sim X\oplus Y $
is not isomorphic to the whole space.
$X_{\mathrm {GM}} \sim X\oplus Y $
is not isomorphic to the whole space.
While indecomposable spaces play a tremendous role [Reference Argyros and Haydon3, Reference Gowers and Maurey18, Reference Maurey27] in the present-day study of nonclassical Banach spaces, a wide variety of Banach function spaces may usually be decomposed, for instance, by restriction to subsets, by taking conditional expectations, and so on. This provides the background for the program set forth by Lindenstrauss to determine the ‘classical’ spaces that are primary.
1.1 Background and history
The term ‘classical Banach space’ – while not formally defined – certainly applies to the space
![]() $C[0,1]$
and to scalar and vector-valued Lebesgue spaces. The space of continuous functions was shown to be primary by Lindenstrauss and Pełczyński [Reference Lindenstrauss and Pełczyński24], who posed the corresponding problem for scalar-valued
$C[0,1]$
and to scalar and vector-valued Lebesgue spaces. The space of continuous functions was shown to be primary by Lindenstrauss and Pełczyński [Reference Lindenstrauss and Pełczyński24], who posed the corresponding problem for scalar-valued
![]() $L_p$
spaces. Its elegant solution by Enflo via Maurey [Reference Maurey26] introduced a ground-breaking method of proof that applies equally well to each of the
$L_p$
spaces. Its elegant solution by Enflo via Maurey [Reference Maurey26] introduced a ground-breaking method of proof that applies equally well to each of the
![]() $L_ p $
spaces
$L_ p $
spaces
![]() $ (1 \le p < \infty )$
. Later alternative proofs were given by Alspach, Enflo and Odell [Reference Alspach, Enflo and Odell1] for
$ (1 \le p < \infty )$
. Later alternative proofs were given by Alspach, Enflo and Odell [Reference Alspach, Enflo and Odell1] for
![]() $L_p $
in the reflexive range
$L_p $
in the reflexive range
![]() $1<p<\infty $
and by Enflo and Starbird [Reference Enflo and Starbird16] for
$1<p<\infty $
and by Enflo and Starbird [Reference Enflo and Starbird16] for
![]() $L_1$
.
$L_1$
.
Exceptionally deep results on the decomposition of Bochner-Lebesgue spaces
![]() $L_p(X)$
are due to Capon [Reference Capon12, Reference Capon11], who obtained that those spaces are primary in the following cases:
$L_p(X)$
are due to Capon [Reference Capon12, Reference Capon11], who obtained that those spaces are primary in the following cases:
-
- X is a Banach space with a symmetric basis, and
 $1 \le p < \infty $
.
$1 \le p < \infty $
. -
-
 $ X = L_ q $
, where
$ X = L_ q $
, where
 $ 1< q < \infty $
and
$ 1< q < \infty $
and
 $ 1< p < \infty $
.
$ 1< p < \infty $
.
This leaves the spaces
![]() $ L_1(L_p) $
and
$ L_1(L_p) $
and
![]() $ L_p(L_1) $
among the most prominent examples of classical Banach spaces for which primariness is open.
$ L_p(L_1) $
among the most prominent examples of classical Banach spaces for which primariness is open.
After Capon’s paper [Reference Capon12], the focus was concentrated mostly on nonseparable Banach spaces, where Bourgain [Reference Bourgain7] developed a very flexible method based on localisation to a sequence of quantitative finite-dimensional factorisation problems. This method led to results like the primariness of
![]() $\mathcal {L}(\ell _2)$
[Reference Blower6] and the primariness of
$\mathcal {L}(\ell _2)$
[Reference Blower6] and the primariness of
![]() $\mathrm {BMO}$
and its predual
$\mathrm {BMO}$
and its predual
![]() $H_1$
by the third author [Reference Müller29].
$H_1$
by the third author [Reference Müller29].
The purpose of the present paper is to prove that
![]() $ L_1(L_p) $
is primary. Our proof works equally well for real and complex-valued functions. Before we describe our work, we review in some detail the development of methods pertaining to the spaces
$ L_1(L_p) $
is primary. Our proof works equally well for real and complex-valued functions. Before we describe our work, we review in some detail the development of methods pertaining to the spaces
![]() $L_p$
and, more broadly, to rearrangement-invariant spaces.
$L_p$
and, more broadly, to rearrangement-invariant spaces.
Projections on those spaces are studied effectively alongside the Haar system and the reproducing properties of its block bases. The methods developed for proving that a particular Lebesgue space
![]() $L_p$
is primary may be divided into two basic classes, depending on whether the Haar system is an unconditional Schauder basis.
$L_p$
is primary may be divided into two basic classes, depending on whether the Haar system is an unconditional Schauder basis.
In case of unconditionality, the most flexible method goes back to the work of Alspach, Enflo and Odell [Reference Alspach, Enflo and Odell1]. For a linear operator T on
![]() $L_p $
, it yields a block basis of the Haar system
$L_p $
, it yields a block basis of the Haar system
![]() $\widetilde {h}_I $
and a bounded sequence of scalars
$\widetilde {h}_I $
and a bounded sequence of scalars
![]() $a_I $
forming an approximate eigensystem of T such that
$a_I $
forming an approximate eigensystem of T such that
and
![]() $\widetilde {h}_I$
spans a complemented copy of the space
$\widetilde {h}_I$
spans a complemented copy of the space
![]() $L_p $
. Thus, when restricted to
$L_p $
. Thus, when restricted to
![]() $ span \widetilde {h}_I$
, the operator T acts as a bounded Haar multiplier. Since the Haar basis is unconditional, the Haar multiplier is invertible if
$ span \widetilde {h}_I$
, the operator T acts as a bounded Haar multiplier. Since the Haar basis is unconditional, the Haar multiplier is invertible if
![]() $ |a_I |> \delta $
for some
$ |a_I |> \delta $
for some
![]() $\delta> 0. $
$\delta> 0. $
Alspach, Enflo and Odell [Reference Alspach, Enflo and Odell1] arrive at equation (1) by ensuring that for
![]() $\varepsilon _{I, J }> 0 $
sufficiently small, the following linearly ordered set of constraints holds true
$\varepsilon _{I, J }> 0 $
sufficiently small, the following linearly ordered set of constraints holds true
where the relation
![]() $\prec $
refers to the lexicographic order on the collection of dyadic intervals. Utilising that the independent
$\prec $
refers to the lexicographic order on the collection of dyadic intervals. Utilising that the independent
![]() $\{-1,+1\}$
-valued Rademacher system
$\{-1,+1\}$
-valued Rademacher system
![]() $\{r_n\}$
is a weak null sequence in
$\{r_n\}$
is a weak null sequence in
![]() $L_p$
,
$L_p$
,
![]() $(1 \le p < \infty )$
, Alspach, Enflo and Odell [Reference Alspach, Enflo and Odell1] obtain, by induction along
$(1 \le p < \infty )$
, Alspach, Enflo and Odell [Reference Alspach, Enflo and Odell1] obtain, by induction along
![]() $\prec $
, the block basis
$\prec $
, the block basis
![]() $ \widetilde {h}_I$
satisfying equation (2).
$ \widetilde {h}_I$
satisfying equation (2).
The Alspach-Enflo-Odell method provides the basic model for the study of operators on function spaces in which the Haar system is unconditional; this applies in particular to rearrangement of invariant spaces in [Reference Johnson, Maurey, Schechtman and Tzafriri20] and [Reference Dosev, Johnson and Schechtman15].
In
![]() $L_1 $
, the Haar system is a Schauder basis but fails to be unconditional. The basic methods for proving that
$L_1 $
, the Haar system is a Schauder basis but fails to be unconditional. The basic methods for proving that
![]() $L_1 $
is primary are due to Enflo via Maurey [Reference Maurey26] on the one hand and Enflo and Starbird [Reference Enflo and Starbird16] on the other hand. For operators T on
$L_1 $
is primary are due to Enflo via Maurey [Reference Maurey26] on the one hand and Enflo and Starbird [Reference Enflo and Starbird16] on the other hand. For operators T on
![]() $L_1 $
, the Enflo-Maurey method yields a block basis of the Haar basis
$L_1 $
, the Enflo-Maurey method yields a block basis of the Haar basis
![]() $\widetilde {h}_I $
and a bounded measurable function g, such that
$\widetilde {h}_I $
and a bounded measurable function g, such that
for
![]() $ f \in \mathrm {span}\{ \widetilde {h}_I\}$
, and
$ f \in \mathrm {span}\{ \widetilde {h}_I\}$
, and
![]() $\widetilde {h}_I$
spans a copy of
$\widetilde {h}_I$
spans a copy of
![]() $L_1 $
. Thus the restricted operator T acts as a bounded multiplication operator and is invertible if
$L_1 $
. Thus the restricted operator T acts as a bounded multiplication operator and is invertible if
![]() $ |g |> \delta $
for some
$ |g |> \delta $
for some
![]() $\delta> 0. $
The full strength of the proof by Enflo-Maurey is applied to show that the representation in equation (3) holds true.
$\delta> 0. $
The full strength of the proof by Enflo-Maurey is applied to show that the representation in equation (3) holds true.
Enflo-Maurey [Reference Maurey26] exhibit in their proof of equation (3) a sequence of bounded scalars
![]() $a_I $
such that
$a_I $
such that
Since the Rademacher system
![]() $\{r_n\}$
is a weakly null sequence in
$\{r_n\}$
is a weakly null sequence in
![]() $L_1$
, equation (4) may be obtained directly by choosing a block basis for which the constraints in equation (2) and
$L_1$
, equation (4) may be obtained directly by choosing a block basis for which the constraints in equation (2) and
hold true. Remarkably, until very recently [Reference Lechner, Motakis, Müller and Schlumprecht22], eigensystem representations such as equation (4) were not exploited in the context of
![]() $L ^1 $
, where the Haar system is not unconditional.
$L ^1 $
, where the Haar system is not unconditional.
The powerful precision of
![]() $L_1$
-constructions with dyadic martingales and block basis of the Haar system is in full display in [Reference Johnson, Maurey and Schechtman19] and [Reference Talagrand36]. Johnson, Maurey and Schechtman [Reference Johnson, Maurey and Schechtman19] determined a normalised weakly null sequence in
$L_1$
-constructions with dyadic martingales and block basis of the Haar system is in full display in [Reference Johnson, Maurey and Schechtman19] and [Reference Talagrand36]. Johnson, Maurey and Schechtman [Reference Johnson, Maurey and Schechtman19] determined a normalised weakly null sequence in
![]() $L_1 $
such that each of its infinite subsequences contains in its span a block basis of the Haar system
$L_1 $
such that each of its infinite subsequences contains in its span a block basis of the Haar system
![]() $\widetilde {h}_I$
, spanning a copy of
$\widetilde {h}_I$
, spanning a copy of
![]() $L_1. $
Thus
$L_1. $
Thus
![]() $L_1 $
fails to satisfy the unconditional subsequence property, a problem posed by Maurey and Rosenthal [Reference Maurey and Rosenthal28]. By contrast, Talagrand [Reference Talagrand36] constructed a dyadic martingale difference sequence
$L_1 $
fails to satisfy the unconditional subsequence property, a problem posed by Maurey and Rosenthal [Reference Maurey and Rosenthal28]. By contrast, Talagrand [Reference Talagrand36] constructed a dyadic martingale difference sequence
![]() $g_{n,k} $
such that neither
$g_{n,k} $
such that neither
![]() $X = \overline {\mathrm {span}\, }^{L_1} \{ g_{n,k} \}$
nor
$X = \overline {\mathrm {span}\, }^{L_1} \{ g_{n,k} \}$
nor
![]() $L_1/X$
contains a copy of
$L_1/X$
contains a copy of
![]() $L_1$
.
$L_1$
.
The investigation of complemented subspaces in Bochner Lebesgue spaces was initiated by Capon [Reference Capon12, Reference Capon11] who pushed hard to further the development of the scalar methods and proved that
![]() $L_p(X) (1\le p < \infty )$
is primary when X is a Banach space with a symmetric basis, say
$L_p(X) (1\le p < \infty )$
is primary when X is a Banach space with a symmetric basis, say
![]() $(x_{k}) .$
Specifically, Capon [Reference Capon12] showed that for an operator T on
$(x_{k}) .$
Specifically, Capon [Reference Capon12] showed that for an operator T on
![]() $L_p(X)$
, there exists a block basis of the Haar basis
$L_p(X)$
, there exists a block basis of the Haar basis
![]() $\widetilde {h}_I $
, a subsequence of the symmetric basis
$\widetilde {h}_I $
, a subsequence of the symmetric basis
![]() $(x_{k_n}) $
and a bounded measurable g such that
$(x_{k_n}) $
and a bounded measurable g such that
for
![]() $ f \in \mathrm {span} \{\widetilde {h}_I \}$
. Thus on
$ f \in \mathrm {span} \{\widetilde {h}_I \}$
. Thus on
![]() $ \mathrm {span} \{\widetilde {h}_I \} \otimes \mathrm {span} \{x_{k_n}\}$
the operator T acts like
$ \mathrm {span} \{\widetilde {h}_I \} \otimes \mathrm {span} \{x_{k_n}\}$
the operator T acts like
![]() $M_g \otimes Id $
, where
$M_g \otimes Id $
, where
![]() $M_g $
is the multiplication operator induced by
$M_g $
is the multiplication operator induced by
![]() $g. $
Simultaneously, Capon shows that the tensor products form an approximate eigensystem,
$g. $
Simultaneously, Capon shows that the tensor products form an approximate eigensystem,
where
![]() $ a_{I }$
is a bounded sequence of scalars and
$ a_{I }$
is a bounded sequence of scalars and
![]() $\widetilde {h}_I$
spans a copy of
$\widetilde {h}_I$
spans a copy of
![]() $L_p $
.
$L_p $
.
In the mixed norm space
![]() $L_p (L_ q) $
where
$L_p (L_ q) $
where
![]() $ 1< q < \infty $
and
$ 1< q < \infty $
and
![]() $ 1< p < \infty $
, the biparameter Haar system forms an unconditional basis. Displaying extraordinary combinatorial strength, Capon [Reference Capon11] exhibited a so-called local product block basis
$ 1< p < \infty $
, the biparameter Haar system forms an unconditional basis. Displaying extraordinary combinatorial strength, Capon [Reference Capon11] exhibited a so-called local product block basis
![]() $ k_{I \times J }$
spanning a complemented copy of
$ k_{I \times J }$
spanning a complemented copy of
![]() $L_p (L_q ) $
such that
$L_p (L_q ) $
such that
1.2 The present paper
Now we describe the main ideas in the approach of the present paper.
Introducing a transitive relation between operators
![]() $S,T$
on a Banach space X, we say that T is a projectional factor of S if there exist transfer operators
$S,T$
on a Banach space X, we say that T is a projectional factor of S if there exist transfer operators
![]() $ A, B \colon X \to X $
such that
$ A, B \colon X \to X $
such that
If merely
![]() $S = ATB$
, without the additional constraint
$S = ATB$
, without the additional constraint
![]() $BA =Id_X$
, we say that T is a factor of S, or equivalently that S factors through T.
$BA =Id_X$
, we say that T is a factor of S, or equivalently that S factors through T.
Clearly, if T is a projectional factor of S and S one of R, then T is a projectional factor of R: that is, being a projectional factor is a transitive relation. Given any operator
![]() $T : L_1(L_p) \to L_1(L_p)$
, the goal is to show that either T or
$T : L_1(L_p) \to L_1(L_p)$
, the goal is to show that either T or
![]() $Id -T$
is a factor of the identity
$Id -T$
is a factor of the identity
![]() $Id : L_1(L_p) \to L_1(L_p)$
. In section 2.1, we expand on the quantitative aspects of the transitive relation in equation (6) and the role it plays in providing a step-by-step reduction of the problem, allowing for the replacement of a given operator with a simpler one that is easier to work with.
$Id : L_1(L_p) \to L_1(L_p)$
. In section 2.1, we expand on the quantitative aspects of the transitive relation in equation (6) and the role it plays in providing a step-by-step reduction of the problem, allowing for the replacement of a given operator with a simpler one that is easier to work with.
Let
![]() $T : L_1(L_p) \to L_1(L_p)$
be a bounded linear operator. It is represented by a matrix
$T : L_1(L_p) \to L_1(L_p)$
be a bounded linear operator. It is represented by a matrix
![]() $T = ( T^{I,J})$
of operators
$T = ( T^{I,J})$
of operators
![]() $ T^{I,J} : L_1 \to L_1 $
, indexed by pairs of dyadic intervals
$ T^{I,J} : L_1 \to L_1 $
, indexed by pairs of dyadic intervals
![]() $(I,J)$
: that is, on
$(I,J)$
: that is, on
![]() $f \in L_1(L_p)$
with Haar expansion
$f \in L_1(L_p)$
with Haar expansion
the operator T acts by
Theorem 6.1, the main result of this paper, asserts that there exists a bounded operator
![]() $ T^{0} :L_1 \to L_1 $
such that
$ T^{0} :L_1 \to L_1 $
such that
meaning there exist bounded transfer operators
![]() $A, B : L_1(L_p) \to L_1(L_p) $
such that
$A, B : L_1(L_p) \to L_1(L_p) $
such that
![]() $ B A = Id _{L_1(L_p)} $
and
$ B A = Id _{L_1(L_p)} $
and

The ideas involved in the proof of Theorem 6.1 are based on the interplay of topological, geometric and probabilistic principles. Specifically, we build on compact families of
![]() $L_1 $
-operators, extracted from
$L_1 $
-operators, extracted from
![]() $ span \{ T^{I,J} \} $
, and large deviation estimates for empirical processes:
$ span \{ T^{I,J} \} $
, and large deviation estimates for empirical processes:
-
(a) (Compactness.) We utilise the Semenov-Uksusov characterisation [Reference Semenov and Uksusov34, Reference Semenov and Uksusov35] of Haar multipliers on
 $L_1 $
and uncover compactness properties of the operators
$L_1 $
and uncover compactness properties of the operators
 $ T^{I,J} : L_1 \to L_1 $
. See Theorem 3.2 and Theorem 3.4.
$ T^{I,J} : L_1 \to L_1 $
. See Theorem 3.2 and Theorem 3.4. -
(b) (Stabilisation.) Large deviation estimates for the empirical distribution method gave rise to a novel connection between factorisation problems on
 $L_ 1 (L_p) $
and the concentration of measure phenomenon. See Lemma 5.3 and Lemma 5.4.
$L_ 1 (L_p) $
and the concentration of measure phenomenon. See Lemma 5.3 and Lemma 5.4.
Step 1. We say that T is a diagonal operator if
![]() $ T^{I,J} = 0$
for
$ T^{I,J} = 0$
for
![]() $ I \neq J , $
in which case we put
$ I \neq J , $
in which case we put
![]() $ T^{L} =T^{L,L}$
. The first step provides the reduction to diagonal operators. Specifically, Theorem 4.1 asserts that for any operator
$ T^{L} =T^{L,L}$
. The first step provides the reduction to diagonal operators. Specifically, Theorem 4.1 asserts that for any operator
![]() $T = ( T^{I,J})$
, there exists a diagonal operator
$T = ( T^{I,J})$
, there exists a diagonal operator
![]() $T_{\mathrm {diag}} =( T^{L} )$
such that
$T_{\mathrm {diag}} =( T^{L} )$
such that
The reduction in equation (10) results from compactness properties for the family of
![]() $L_1 $
operators
$L_1 $
operators
![]() $ T^{I,J}$
established in Theorem 3.2 and Theorem 3.4. Specifically, if
$ T^{I,J}$
established in Theorem 3.2 and Theorem 3.4. Specifically, if
![]() $ f \in L_1$
, then the set
$ f \in L_1$
, then the set
if, moreover,
![]() $T^{I,J}$
satisfies uniform off-diagonal estimates
$T^{I,J}$
satisfies uniform off-diagonal estimates
then, for
![]() $ \eta> 0 ,$
there exists a stopping time collection of dyadic intervals
$ \eta> 0 ,$
there exists a stopping time collection of dyadic intervals
![]() $ \mathcal {A}$
satisfying
$ \mathcal {A}$
satisfying
![]() $|\limsup \mathcal {A}|> 1 -\eta $
such that the set of operators
$|\limsup \mathcal {A}|> 1 -\eta $
such that the set of operators
Recall that
![]() $ \mathcal {A} \subseteq \mathcal {D}$
is a stopping time collection if for
$ \mathcal {A} \subseteq \mathcal {D}$
is a stopping time collection if for
![]() $K, L \in \mathcal {A} $
and
$K, L \in \mathcal {A} $
and
![]() $ J \in \mathcal {D} $
, the assumption
$ J \in \mathcal {D} $
, the assumption
![]() $ K \subset J \subset L $
implies that
$ K \subset J \subset L $
implies that
![]() $ J \in \mathcal {A} .$
By Theorem 2.6, the orthogonal projection
$ J \in \mathcal {A} .$
By Theorem 2.6, the orthogonal projection
is bounded on
![]() $L_1 $
when
$L_1 $
when
![]() $ \mathcal {A} $
is a stopping time collection of dyadic intervals.
$ \mathcal {A} $
is a stopping time collection of dyadic intervals.
Step 2. Next we show that it suffices to prove the factorisation in equation (9) for diagonal operators satisfying uniform off-diagonal estimates. We say that
![]() $ T = (R^{L}) $
is a reduced diagonal operator if the
$ T = (R^{L}) $
is a reduced diagonal operator if the
![]() $R^L : L_1 \to L_1 $
satisfy
$R^L : L_1 \to L_1 $
satisfy
Proposition 5.6 asserts that there exists a reduced diagonal operator
![]() $ T^{\mathrm {red}}_{\mathrm {diag}} = (R^{L}) $
satisfying equation (14), such that
$ T^{\mathrm {red}}_{\mathrm {diag}} = (R^{L}) $
satisfying equation (14), such that
To prove equation (15), we use the compactness properties of
![]() $T_{\mathrm {diag}} = (T^{L}) $
together with measure concentration estimates [Reference Bourgain, Lindenstrauss and Milman8, Reference Schechtman33] associated to the empirical distribution method. See Lemma 5.3 and Lemma 5.4.
$T_{\mathrm {diag}} = (T^{L}) $
together with measure concentration estimates [Reference Bourgain, Lindenstrauss and Milman8, Reference Schechtman33] associated to the empirical distribution method. See Lemma 5.3 and Lemma 5.4.
Step 3. Next we show that we may replace reduced diagonal operators by stable diagonal operators. We say that
![]() $ T^{\mathrm {stbl}}_{\mathrm {diag}} = (S^{L}) $
is a stable diagonal operator if
$ T^{\mathrm {stbl}}_{\mathrm {diag}} = (S^{L}) $
is a stable diagonal operator if
for dyadic intervals
![]() $M, L $
satisfying
$M, L $
satisfying
![]() $ L \subseteq M$
, we obtain in Proposition 5.2 that for any reduced diagonal operator
$ L \subseteq M$
, we obtain in Proposition 5.2 that for any reduced diagonal operator
![]() $ T^{\mathrm {red}}_{\mathrm {diag}} $
, there exists a stable diagonal operator
$ T^{\mathrm {red}}_{\mathrm {diag}} $
, there exists a stable diagonal operator
![]() $ T^{\mathrm {stbl}}_{\mathrm {diag}} $
such that
$ T^{\mathrm {stbl}}_{\mathrm {diag}} $
such that
We verify equation (17), exploiting again the compactness properties of
![]() $T^{\mathrm {red}}_{\mathrm {diag}} = (R^{L}) $
in tandem with the probabilistic estimates of Lemma 5.3 and Lemma 5.4.
$T^{\mathrm {red}}_{\mathrm {diag}} = (R^{L}) $
in tandem with the probabilistic estimates of Lemma 5.3 and Lemma 5.4.
Step 4. Proposition 6.2 provides the final step of the argument. It asserts that for any stable diagonal operator
![]() $ T^{\mathrm {stbl}}_{\mathrm {diag}} =(S^L)$
, there exists a bounded operator
$ T^{\mathrm {stbl}}_{\mathrm {diag}} =(S^L)$
, there exists a bounded operator
![]() $ T^{0} :L_1 \to L_1 $
such that
$ T^{0} :L_1 \to L_1 $
such that
To prove equation (18), we set up a telescoping chain of operators connecting any of the
![]() $ S^L $
to
$ S^L $
to
![]() $S^{[0,1]} $
and invoke the stability estimates in equation (16) available for the operators
$S^{[0,1]} $
and invoke the stability estimates in equation (16) available for the operators
![]() $S^I $
when
$S^I $
when
![]() $ L \subset I \subset [0,1]. $
Thus we may finally take
$ L \subset I \subset [0,1]. $
Thus we may finally take
![]() $T^0 = S^{[0,1]} .$
$T^0 = S^{[0,1]} .$
Step 5. Retracing our steps, taking into account that the notion of projectional factors forms a transitive relation, yields equation (9).
2 Preliminaries
2.1 Factors and projectional factors up to approximation
A common strategy in proving the primariness of spaces such as
![]() $L_p$
is to study the behaviour of a bounded linear operator on a
$L_p$
is to study the behaviour of a bounded linear operator on a
![]() $\sigma $
-subalgebra on a subset of
$\sigma $
-subalgebra on a subset of
![]() $[0,1)$
of positive measure. This process may have to be repeated several times. We introduce some language that will make this process notationally easier.
$[0,1)$
of positive measure. This process may have to be repeated several times. We introduce some language that will make this process notationally easier.
Definition 2.1. Let X be a Banach space,
![]() $T,S:X\to X$
be bounded linear operators and
$T,S:X\to X$
be bounded linear operators and
![]() $C\geq 1$
,
$C\geq 1$
,
![]() $\varepsilon \geq 0$
.
$\varepsilon \geq 0$
.
-
(a) We say that T is a C-factor of S with error
 $\varepsilon $
if there exist
$\varepsilon $
if there exist
 $A,B:X\to X$
with
$A,B:X\to X$
with
 $\|BTA-S\| \leq \varepsilon $
and
$\|BTA-S\| \leq \varepsilon $
and
 $\|A\|\|B\|\leq C$
. We may also say that
$\|A\|\|B\|\leq C$
. We may also say that
 $S C$
-factors through Twith error
$S C$
-factors through Twith error
 $\varepsilon $
.
$\varepsilon $
. -
(b) We say that T is a C-projectional factor of S with error
 $\varepsilon $
if there exists a complemented subspace Y of X that is isomorphic to X with associated projection and isomorphism
$\varepsilon $
if there exists a complemented subspace Y of X that is isomorphic to X with associated projection and isomorphism
 $P,A:X\to Y$
(i.e.,
$P,A:X\to Y$
(i.e.,
 $A^{-1} P A$
is the identity on X), so that
$A^{-1} P A$
is the identity on X), so that
 $\|A^{-1}PTA - S\| \leq \varepsilon $
and
$\|A^{-1}PTA - S\| \leq \varepsilon $
and
 $\|A\|\|A^{-1}P\|\leq C$
. We may also say that
$\|A\|\|A^{-1}P\|\leq C$
. We may also say that
 $S C$
-projectionally factors through Twith error
$S C$
-projectionally factors through Twith error
 $\varepsilon $
.
$\varepsilon $
.
When the error is
![]() $\varepsilon = 0$
, we will simply say that T is a C-factor or C-projectional factor of S.
$\varepsilon = 0$
, we will simply say that T is a C-factor or C-projectional factor of S.
Remark 2.2. If T is a C-projectional factor of S with error
![]() $\varepsilon $
, then
$\varepsilon $
, then
![]() $I-T$
is a C-projectional factor of
$I-T$
is a C-projectional factor of
![]() $I-S$
with error
$I-S$
with error
![]() $\varepsilon $
. Indeed, if P and A are as in Definition (b), then
$\varepsilon $
. Indeed, if P and A are as in Definition (b), then
![]() $PA = A$
and therefore
$PA = A$
and therefore
![]() $A^{-1}P(I-T)A = I - A^{-1}PTA$
: that is,
$A^{-1}P(I-T)A = I - A^{-1}PTA$
: that is,
![]() $\|A^{-1}P(I-T)A - (I-S)\| \leq \varepsilon $
.
$\|A^{-1}P(I-T)A - (I-S)\| \leq \varepsilon $
.
In a certain sense, being an approximate factor or projectional factor is a transitive property.
Proposition 2.3. Let X be a Banach space and
![]() $R,S,T:X\to X$
be bounded linear operators.
$R,S,T:X\to X$
be bounded linear operators.
-
(a) If T is a C-factor of S with error
 $\varepsilon $
and S is a D-factor of R with error
$\varepsilon $
and S is a D-factor of R with error
 $\delta $
, then T is a
$\delta $
, then T is a
 $CD$
-factor of R with error
$CD$
-factor of R with error
 $D\varepsilon +\delta $
.
$D\varepsilon +\delta $
. -
(b) If T is a C-projectional factor of S with error
 $\varepsilon $
and S is a D-projectional factor of R with error
$\varepsilon $
and S is a D-projectional factor of R with error
 $\delta $
, then T is a
$\delta $
, then T is a
 $CD$
-projectional factor or R with error
$CD$
-projectional factor or R with error
 $D\varepsilon +\delta $
.
$D\varepsilon +\delta $
.
Proof. The first statement is straightforward, and thus we only provide a proof of the second one. Let Y and Z be complemented subspaces of X, which are isomorphic to X. Let
![]() $P:X\to Y$
and
$P:X\to Y$
and
![]() $Q:X\to Z$
be the associated projections, and
$Q:X\to Z$
be the associated projections, and
![]() $A:X\to Y$
and
$A:X\to Y$
and
![]() $B:X\to Z$
the associated isomorphisms satisfying
$B:X\to Z$
the associated isomorphisms satisfying
![]() $\|A\|\|A^{-1}P\| \leq C$
,
$\|A\|\|A^{-1}P\| \leq C$
,
![]() $\|B\|\|B^{-1}Q\|\leq D$
.
$\|B\|\|B^{-1}Q\|\leq D$
.
![]() $\|A^{-1}PT - S\| \leq \varepsilon $
and
$\|A^{-1}PT - S\| \leq \varepsilon $
and
![]() $\|B^{-1}QSB - R\| \leq \delta $
.
$\|B^{-1}QSB - R\| \leq \delta $
.
We define
![]() $\tilde P = AQA^{-1}P$
and
$\tilde P = AQA^{-1}P$
and
![]() $\tilde A = AB$
. Then
$\tilde A = AB$
. Then
![]() $\tilde P$
is a projection onto
$\tilde P$
is a projection onto
![]() $\tilde A[X]$
and
$\tilde A[X]$
and
![]() $\|\tilde P\|\|\tilde A^{-1}P\| \leq CD$
. We obtain
$\|\tilde P\|\|\tilde A^{-1}P\| \leq CD$
. We obtain
and thus
![]() $\|B^{-1}QA^{-1}PTAB - R\| \leq D\varepsilon +\delta $
. Finally, observe that
$\|B^{-1}QA^{-1}PTAB - R\| \leq D\varepsilon +\delta $
. Finally, observe that
and thus
![]() $\|\tilde A^{-1}\tilde PT\tilde A - R\|\leq D\varepsilon + \delta $
.
$\|\tilde A^{-1}\tilde PT\tilde A - R\|\leq D\varepsilon + \delta $
.
The following explains the relation between primariness and approximate projectional factors.
Proposition 2.4. Let X be a Banach space that satisfies Pełczyński’s accordion property: that is, for some
![]() $1\leq p\leq \infty $
, we have that
$1\leq p\leq \infty $
, we have that
![]() $X\simeq \ell _p(X)$
. Assume that there exist
$X\simeq \ell _p(X)$
. Assume that there exist
![]() $C\geq 1$
and
$C\geq 1$
and
![]() $0<\varepsilon <1/2$
so that every bounded linear operator
$0<\varepsilon <1/2$
so that every bounded linear operator
![]() $T:X\to X$
is a C-projectional factor with error
$T:X\to X$
is a C-projectional factor with error
![]() $\varepsilon $
of a scalar operator: that is, a scalar multiple of the identity. Then for every bounded linear operator
$\varepsilon $
of a scalar operator: that is, a scalar multiple of the identity. Then for every bounded linear operator
![]() $T:X\to X$
, the identity
$T:X\to X$
, the identity
![]() $2C/(1-2\varepsilon )$
factors through either T or
$2C/(1-2\varepsilon )$
factors through either T or
![]() $I-T$
. In particular, X is primary.
$I-T$
. In particular, X is primary.
Proof. Let Y be a subspace of X that is isomorphic to X and complemented in X, with associated projection and isomorphism
![]() $P,A:X\to Y$
, so that
$P,A:X\to Y$
, so that
![]() $\|A^{-1}P\|\|A\|\leq C$
and so that there exists a scalar
$\|A^{-1}P\|\|A\|\leq C$
and so that there exists a scalar
![]() $\lambda $
with
$\lambda $
with
![]() $\|(A^{-1}P)TA - \lambda I\| \leq \varepsilon $
. If
$\|(A^{-1}P)TA - \lambda I\| \leq \varepsilon $
. If
![]() $|\lambda | \geq 1/2$
, then
$|\lambda | \geq 1/2$
, then
 $$\begin{align*}\big\|\underbrace{\lambda^{-1}A^{-1}PTA}_{=:B} - I\big\| \leq 2\varepsilon <1\end{align*}$$
$$\begin{align*}\big\|\underbrace{\lambda^{-1}A^{-1}PTA}_{=:B} - I\big\| \leq 2\varepsilon <1\end{align*}$$
and thus
![]() $B^{-1}$
exists with
$B^{-1}$
exists with
![]() $\|B^{-1}\| \leq 1/(1-2\varepsilon )$
. We obtain that if
$\|B^{-1}\| \leq 1/(1-2\varepsilon )$
. We obtain that if
![]() $S = B^{-1}\lambda ^{-1}A^{-1}P$
, then
$S = B^{-1}\lambda ^{-1}A^{-1}P$
, then
![]() $STA = I$
and
$STA = I$
and
![]() $\|S\|\|A\| \leq 2C/(1-2\varepsilon )$
. If, on the other hand
$\|S\|\|A\| \leq 2C/(1-2\varepsilon )$
. If, on the other hand
![]() $|\lambda | <1/2$
, then, because
$|\lambda | <1/2$
, then, because
![]() $\|A^{-1}P(I-T)A - (1-\lambda )I\|\leq \varepsilon $
, we achieve the same conclusion for
$\|A^{-1}P(I-T)A - (1-\lambda )I\|\leq \varepsilon $
, we achieve the same conclusion for
![]() $I-T$
instead of T.
$I-T$
instead of T.
If
![]() $X = Y\oplus Z$
and
$X = Y\oplus Z$
and
![]() $Q:X\to Y$
is a projection, then we deduce that either Y or Z contains a complemented subspace isomorphic to X. To see that we can assume that for some scalar
$Q:X\to Y$
is a projection, then we deduce that either Y or Z contains a complemented subspace isomorphic to X. To see that we can assume that for some scalar
![]() $\lambda $
, with
$\lambda $
, with
![]() $|\lambda |\ge 1/2$
, Q is a C-projectional factor with error
$|\lambda |\ge 1/2$
, Q is a C-projectional factor with error
![]() $\varepsilon \in (0,1/2)$
of
$\varepsilon \in (0,1/2)$
of
![]() $\lambda I$
. Otherwise, we replace Q by
$\lambda I$
. Otherwise, we replace Q by
![]() $I-Q$
. From what we have proved so far, we deduce that there are operators
$I-Q$
. From what we have proved so far, we deduce that there are operators
![]() $S,A :X\to X$
so that
$S,A :X\to X$
so that
![]() $SQA = I$
. Then
$SQA = I$
. Then
![]() $W = QA(X)$
is a subspace of Y that is isomorphic to X. It is also complemented via the projection
$W = QA(X)$
is a subspace of Y that is isomorphic to X. It is also complemented via the projection
![]() $R = (S|_W)^{-1}S:X\to W$
. So we obtain that Y is a complemented subspace of X and X is isomorphic to complemented subspace of Y. Since in addition X satisfies the accordion property, it follows from Pełczyński’s famous classical argument from [Reference Pełczyński30] that
$R = (S|_W)^{-1}S:X\to W$
. So we obtain that Y is a complemented subspace of X and X is isomorphic to complemented subspace of Y. Since in addition X satisfies the accordion property, it follows from Pełczyński’s famous classical argument from [Reference Pełczyński30] that
![]() $X\simeq Y$
. Similarly, if
$X\simeq Y$
. Similarly, if
![]() $(I-Q)$
is a factor of the identity, we deduce
$(I-Q)$
is a factor of the identity, we deduce
![]() $X\simeq Z$
.
$X\simeq Z$
.
At this point, it is appropriate to point out that the above proposition applies to the space
![]() $L_1(X)$
for any Banach space X. Indeed,
$L_1(X)$
for any Banach space X. Indeed,
![]() $L_1(X)$
is isomorphic to an
$L_1(X)$
is isomorphic to an
![]() $\ell _1$
sum of infinitely many copies of itself (see, e.g., [Reference Wojtaszczyk41, Example 22(a), page 44]).
$\ell _1$
sum of infinitely many copies of itself (see, e.g., [Reference Wojtaszczyk41, Example 22(a), page 44]).
2.2 The Haar system in
 $L_1$
$L_1$
We denote by
![]() $L_1$
the space of all (equivalence classes of) integrable scalar functions f with domain
$L_1$
the space of all (equivalence classes of) integrable scalar functions f with domain
![]() $[0,1)$
endowed with the norm
$[0,1)$
endowed with the norm
![]() $\|f\|_1 = \int _0^1|f(s)| ds$
. We will denote the Lebesgue measure of a measurable subset A of
$\|f\|_1 = \int _0^1|f(s)| ds$
. We will denote the Lebesgue measure of a measurable subset A of
![]() $[0,1)$
by
$[0,1)$
by
![]() $|A|$
.
$|A|$
.
We denote by
![]() $\mathcal {D}$
the collection of all dyadic intervals in
$\mathcal {D}$
the collection of all dyadic intervals in
![]() $[0,1)$
, namely
$[0,1)$
, namely
We define the bijective function
![]() $\iota : \mathcal {D}\to \{2,3,\ldots \}$
by
$\iota : \mathcal {D}\to \{2,3,\ldots \}$
by
The function
![]() $\iota $
defines a linear order on
$\iota $
defines a linear order on
![]() $\mathcal {D}$
. We recall the definition of the Haar system
$\mathcal {D}$
. We recall the definition of the Haar system
![]() $(h_I)_{I\in \mathcal {D}}$
. For
$(h_I)_{I\in \mathcal {D}}$
. For
![]() $I = [(i-1)/2^j,i/2^j)\in \mathcal {D}$
, we define
$I = [(i-1)/2^j,i/2^j)\in \mathcal {D}$
, we define
![]() $I^+, I^-\in \mathcal {D}$
as follows:
$I^+, I^-\in \mathcal {D}$
as follows:
![]() $I^+ = [(i-1)/2^j,(2i-1)/2^{j+1})$
,
$I^+ = [(i-1)/2^j,(2i-1)/2^{j+1})$
,
![]() $I^- = [(2i-1)/2^{j+1},i/2^j)$
, and
$I^- = [(2i-1)/2^{j+1},i/2^j)$
, and
We additionally define
![]() $h_\emptyset = \chi _{[0,1)}$
and
$h_\emptyset = \chi _{[0,1)}$
and
![]() $\mathcal {D}^+ = \mathcal {D}\cup \{\emptyset \}$
. We also define
$\mathcal {D}^+ = \mathcal {D}\cup \{\emptyset \}$
. We also define
![]() $\iota (\emptyset ) = 1$
. Then
$\iota (\emptyset ) = 1$
. Then
![]() $(h_I)_{I\in \mathcal {D}^+}$
is a monotone Schauder basis of
$(h_I)_{I\in \mathcal {D}^+}$
is a monotone Schauder basis of
![]() $L_1$
, with the linear order induced by
$L_1$
, with the linear order induced by
![]() $\iota $
. Henceforth, whenever we write
$\iota $
. Henceforth, whenever we write
![]() $\sum _{I\in \mathcal {D}^+}$
, we will always mean the sum is taken with this linear order
$\sum _{I\in \mathcal {D}^+}$
, we will always mean the sum is taken with this linear order
![]() $\iota $
.
$\iota $
.
For each
![]() $n\in \mathbb {N}\cup \{0\}$
, we define
$n\in \mathbb {N}\cup \{0\}$
, we define
An important realisation that will be used multiple times in the sequel is the following. Let
![]() $I\in \mathcal {D}$
. Then there exist a unique
$I\in \mathcal {D}$
. Then there exist a unique
![]() $k_0 \in \mathbb {N}$
and a unique decreasing sequence of intervals
$k_0 \in \mathbb {N}$
and a unique decreasing sequence of intervals
![]() $(I_k)_{k=0}^{k_0}$
in
$(I_k)_{k=0}^{k_0}$
in
![]() $(\mathcal {D}^+)$
so that
$(\mathcal {D}^+)$
so that
![]() $I_0 = \emptyset $
,
$I_0 = \emptyset $
,
![]() $I_1 = [0,1)$
and
$I_1 = [0,1)$
and
![]() $I_{k_0}=I$
; and for
$I_{k_0}=I$
; and for
![]() $k=1,2, \ldots , k_{0-1}$
,
$k=1,2, \ldots , k_{0-1}$
,
![]() $I_{k+1}=I^+_k$
or
$I_{k+1}=I^+_k$
or
![]() $I_{k+1}=I^-_k$
. In other words,
$I_{k+1}=I^-_k$
. In other words,
![]() $(I_k)_{k=1}^{k_0}$
consists of all elements of
$(I_k)_{k=1}^{k_0}$
consists of all elements of
![]() $\mathcal D^+$
that contain I, decreasingly ordered. For
$\mathcal D^+$
that contain I, decreasingly ordered. For
![]() $k=1,2, \ldots , k_0-1$
, put
$k=1,2, \ldots , k_0-1$
, put
![]() $\theta _k = 1$
, if
$\theta _k = 1$
, if
![]() $I_{k+1} = I_k^+$
and
$I_{k+1} = I_k^+$
and
![]() $\theta _k = -1$
if
$\theta _k = -1$
if
![]() $I_{k+1} = I_k^-$
. We then have the following formula, already discovered by Haar:
$I_{k+1} = I_k^-$
. We then have the following formula, already discovered by Haar:
 $$ \begin{align} |I|^{-1}\chi_I = |I_{k_0}|^{-1}\chi_{I_{k_0}} = h_{I_0} + \sum_{k=1}^{k_0-1}\theta_k|I_k|^{-1}h_{I_k}. \end{align} $$
$$ \begin{align} |I|^{-1}\chi_I = |I_{k_0}|^{-1}\chi_{I_{k_0}} = h_{I_0} + \sum_{k=1}^{k_0-1}\theta_k|I_k|^{-1}h_{I_k}. \end{align} $$
Note that in the above representation, if we define
![]() $I_{k_0} = I$
, then
$I_{k_0} = I$
, then
![]() $I_k = I_{k-1}^-$
or
$I_k = I_{k-1}^-$
or
![]() $I_k = I_{k-1}^+$
for
$I_k = I_{k-1}^+$
for
![]() $k=2,\ldots ,k_0$
. To simplify notation, we will henceforth make the convention
$k=2,\ldots ,k_0$
. To simplify notation, we will henceforth make the convention
![]() $\theta _0 = 1$
and
$\theta _0 = 1$
and
![]() $|I_0|^{-1} = |\emptyset |^{-1} = 1$
to be able to write
$|I_0|^{-1} = |\emptyset |^{-1} = 1$
to be able to write
 $$ \begin{align} |I_{k_0}|^{-1}\chi_{I_{k_0}} = \sum_{k=0}^{k_0-1}\theta_k|I_k|^{-1}h_{I_k}. \end{align} $$
$$ \begin{align} |I_{k_0}|^{-1}\chi_{I_{k_0}} = \sum_{k=0}^{k_0-1}\theta_k|I_k|^{-1}h_{I_k}. \end{align} $$
This representation will be used multiple times in this paper.
A relevant definition is that of
![]() $[\mathcal {D}^+]$
, the collection of all sequences
$[\mathcal {D}^+]$
, the collection of all sequences
![]() $(I_k)_{k=0}^\infty $
in
$(I_k)_{k=0}^\infty $
in
![]() $\mathcal {D}^+$
so that
$\mathcal {D}^+$
so that
![]() $I_0 = \emptyset $
,
$I_0 = \emptyset $
,
![]() $I_1 = [0,1)$
, and for each
$I_1 = [0,1)$
, and for each
![]() $k\in \mathbb {N}$
,
$k\in \mathbb {N}$
,
![]() $I_{k+1} = I_k^+$
or
$I_{k+1} = I_k^+$
or
![]() $I_{k+1} = I_k^-$
. Note that for
$I_{k+1} = I_k^-$
. Note that for
![]() $(I_k)_{k=0}^\infty \in [\mathcal {D}^+]$
and
$(I_k)_{k=0}^\infty \in [\mathcal {D}^+]$
and
![]() $k\in \mathbb {N}$
,
$k\in \mathbb {N}$
,
![]() $I_k\in \mathcal {D}_{k-1}$
. Each
$I_k\in \mathcal {D}_{k-1}$
. Each
![]() $(I_k)_{k=0}^\infty $
defines a sequence
$(I_k)_{k=0}^\infty $
defines a sequence
![]() $(\theta _k)_{k=1}^\infty $
as described in the paragraph above. This yields a bijection between
$(\theta _k)_{k=1}^\infty $
as described in the paragraph above. This yields a bijection between
![]() $[\mathcal {D}^+]$
and
$[\mathcal {D}^+]$
and
![]() $\{-1,1\}^{\mathbb {N}}$
. This fact will be used more than once. On
$\{-1,1\}^{\mathbb {N}}$
. This fact will be used more than once. On
![]() $\{-1,1\}^{\mathbb {N}}$
, we will consider the product of the uniform distribution on
$\{-1,1\}^{\mathbb {N}}$
, we will consider the product of the uniform distribution on
![]() $\{-1,1\}$
, which via this bijection generates a probability on
$\{-1,1\}$
, which via this bijection generates a probability on
![]() $[\mathcal {D}^+]$
, which we will also denote by
$[\mathcal {D}^+]$
, which we will also denote by
![]() $|\cdot |$
. Also, we consider on
$|\cdot |$
. Also, we consider on
![]() $[\mathcal D^+] $
the image topology of the product of the discrete topology on
$[\mathcal D^+] $
the image topology of the product of the discrete topology on
![]() $\{-1,1\}$
via that bijection.
$\{-1,1\}$
via that bijection.
2.3 Haar multipliers on
 $L_1$
$L_1$
A Haar multiplier is a linear map D, defined on the linear span of the Haar system, for which every Haar vector
![]() $h_I$
is an eigenvector with eigenvalue
$h_I$
is an eigenvector with eigenvalue
![]() $a_I$
. We denote the space of bounded Haar multipliers
$a_I$
. We denote the space of bounded Haar multipliers
![]() $D:L_1\to L_1$
by
$D:L_1\to L_1$
by
![]() $\mathcal {L}_{HM}(L_1)$
. In this subsection, we recall a formula for the norm of a Haar multiplier that was observed by Semenov and Uksusov in [Reference Semenov and Uksusov34, Reference Semenov and Uksusov35]. We then use Haar multipliers to sketch a proof of the fact that every bounded linear operator on
$\mathcal {L}_{HM}(L_1)$
. In this subsection, we recall a formula for the norm of a Haar multiplier that was observed by Semenov and Uksusov in [Reference Semenov and Uksusov34, Reference Semenov and Uksusov35]. We then use Haar multipliers to sketch a proof of the fact that every bounded linear operator on
![]() $L_1$
is an approximate 1-projectional factor of a scalar operator.
$L_1$
is an approximate 1-projectional factor of a scalar operator.
This recent formula of Semenov and Uksusov is a very elegant characterisation of boundedness on Haar multipliers on
![]() $L_1$
. In that spirit, Girardi studied related operators on
$L_1$
. In that spirit, Girardi studied related operators on
![]() $L_p$
and
$L_p$
and
![]() $L_p(X)$
of a multiplier type [Reference Girardi17]. Wark has since simplified the proof of Semenov-Uksusov [Reference Wark38] as well as extended the formula to the vector-valued case [Reference Wark39, Reference Wark40].
$L_p(X)$
of a multiplier type [Reference Girardi17]. Wark has since simplified the proof of Semenov-Uksusov [Reference Wark38] as well as extended the formula to the vector-valued case [Reference Wark39, Reference Wark40].
Proposition 2.5. Let
![]() $(I_k)_{k=0}^\infty \in [\mathcal {D}^+]$
be associated to
$(I_k)_{k=0}^\infty \in [\mathcal {D}^+]$
be associated to
![]() $(\theta _k)_{k=1}^\infty \in \{-1,1\}^{\mathbb {N}}$
. For
$(\theta _k)_{k=1}^\infty \in \{-1,1\}^{\mathbb {N}}$
. For
![]() $k\in \mathbb {N}$
define
$k\in \mathbb {N}$
define
![]() $B_k = I_k\setminus I_{k+1}$
, and let
$B_k = I_k\setminus I_{k+1}$
, and let
![]() $(a_k)_{k=0}^n$
be a sequence of scalars.
$(a_k)_{k=0}^n$
be a sequence of scalars.
Then we have
 $$ \begin{align} \frac{1}{3}\Big(\sum_{k=1}^n|a_k - a_{k-1}| + |a_n|\Big) \leq \left\|\sum_{k=0}^na_k\theta_k|I_k|^{-1} h_{I_k}\right\|_{L_1} \leq \sum_{k=1}^n|a_k - a_{k-1}| + |a_n|, \end{align} $$
$$ \begin{align} \frac{1}{3}\Big(\sum_{k=1}^n|a_k - a_{k-1}| + |a_n|\Big) \leq \left\|\sum_{k=0}^na_k\theta_k|I_k|^{-1} h_{I_k}\right\|_{L_1} \leq \sum_{k=1}^n|a_k - a_{k-1}| + |a_n|, \end{align} $$
and for any
![]() $1\le m< n$
,
$1\le m< n$
,
 $$ \begin{align} & \left\|\Big(\sum_{k=0}^na_k\theta_k|I_k|^{-1} h_{I_k}\Big)\big|_{\bigcup_{j=m}^n B_j}\right\|_{L_1}\ge \frac{1}{3}\Big(\sum_{k=m+1}^n|a_k - a_{k-1}|+|a_n|\Big). \end{align} $$
$$ \begin{align} & \left\|\Big(\sum_{k=0}^na_k\theta_k|I_k|^{-1} h_{I_k}\Big)\big|_{\bigcup_{j=m}^n B_j}\right\|_{L_1}\ge \frac{1}{3}\Big(\sum_{k=m+1}^n|a_k - a_{k-1}|+|a_n|\Big). \end{align} $$
Proof. Note that the sequence
![]() $(B_k)_{k=1}^\infty $
is a partition of
$(B_k)_{k=1}^\infty $
is a partition of
![]() $[0,1)$
, and for
$[0,1)$
, and for
![]() $k\in \mathbb {N}$
,
$k\in \mathbb {N}$
,
![]() $B_k$
is the set in
$B_k$
is the set in
![]() $[0,1]$
of measure
$[0,1]$
of measure
![]() $2^{-k}$
on which
$2^{-k}$
on which
![]() $\theta _k h_{I_k}$
takes the value
$\theta _k h_{I_k}$
takes the value
![]() $-1$
. Let
$-1$
. Let
![]() $f = a_0 h_\emptyset + \sum _{k=1}^n \theta _ka_k|I_k|^{-1}h_{I_k}$
. For
$f = a_0 h_\emptyset + \sum _{k=1}^n \theta _ka_k|I_k|^{-1}h_{I_k}$
. For
![]() $k\in \mathbb {N}$
, put
$k\in \mathbb {N}$
, put
![]() $b_k = a_k$
if
$b_k = a_k$
if
![]() $k\leq n$
and
$k\leq n$
and
![]() $b_k = 0$
otherwise. For each
$b_k = 0$
otherwise. For each
![]() $k\in \mathbb {N}$
, the function f is constant on
$k\in \mathbb {N}$
, the function f is constant on
![]() $B_k$
and in fact for
$B_k$
and in fact for
![]() $s\in B_k$
, we have
$s\in B_k$
, we have
 $$ \begin{align*} f(s) =b_0 + \sum_{j=1}^{k-1}|I_j|^{-1}b_j - |I_k|^{-1}b_k = b_0 + \sum_{j=1}^{k-1}2^{j-1}b_j - 2^{k-1}b_k =: c_k. \end{align*} $$
$$ \begin{align*} f(s) =b_0 + \sum_{j=1}^{k-1}|I_j|^{-1}b_j - |I_k|^{-1}b_k = b_0 + \sum_{j=1}^{k-1}2^{j-1}b_j - 2^{k-1}b_k =: c_k. \end{align*} $$
Therefore, for any
![]() $m=1,2,\ldots n$
,
$m=1,2,\ldots n$
,
 $$ \begin{align} \left\|f \chi_{\bigcup_{j=m}^n B_j} \right\|_{L_1} = \sum_{k=m}^\infty |X_k|, \end{align} $$
$$ \begin{align} \left\|f \chi_{\bigcup_{j=m}^n B_j} \right\|_{L_1} = \sum_{k=m}^\infty |X_k|, \end{align} $$
where for each
![]() $k\in \mathbb {N}$
,
$k\in \mathbb {N}$
,
 $$\begin{align*}X_k = \frac{c_k}{2^{k}} = \frac{1}{2^{k}}b_{0} + \sum_{j=1}^{k-1}\frac{2^{j-1}}{2^{k}}b_j - \frac{1}{2}b_k.\end{align*}$$
$$\begin{align*}X_k = \frac{c_k}{2^{k}} = \frac{1}{2^{k}}b_{0} + \sum_{j=1}^{k-1}\frac{2^{j-1}}{2^{k}}b_j - \frac{1}{2}b_k.\end{align*}$$
Putting
![]() $X_0 = 0$
, a calculation yields that for all
$X_0 = 0$
, a calculation yields that for all
![]() $k\in \mathbb {N}$
,
$k\in \mathbb {N}$
,
Applying the triangle inequality to equations (23) and (24), we conclude
 $$ \begin{align*} \| f\|_{L_1}&=\sum_{k=m}^\infty |X_k|=\sum_{k=1}^\infty 2|X_k|-|X_{k-1}|\\ &\le \sum_{k=1}^\infty |2X_k -X_{k-1}|=\sum_{k=1}^\infty|b_k-b_{k-1}|, \end{align*} $$
$$ \begin{align*} \| f\|_{L_1}&=\sum_{k=m}^\infty |X_k|=\sum_{k=1}^\infty 2|X_k|-|X_{k-1}|\\ &\le \sum_{k=1}^\infty |2X_k -X_{k-1}|=\sum_{k=1}^\infty|b_k-b_{k-1}|, \end{align*} $$
which yields the upper bound of equation (21). The lower bound is proved with a similar computation. To obtain equation (22), we deduce from equation (24)
 $$ \begin{align*} &\sum_{k=m+1}^\infty |X_k| \ge\frac12 \sum_{k=m+1}^\infty |b_k-b_{k-1}|-\frac12\sum_{k=m} |X_k| \end{align*} $$
$$ \begin{align*} &\sum_{k=m+1}^\infty |X_k| \ge\frac12 \sum_{k=m+1}^\infty |b_k-b_{k-1}|-\frac12\sum_{k=m} |X_k| \end{align*} $$
and therefore
 $$ \begin{align*} & \frac32 \sum_{k=m+1}^\infty |X_k| +\frac12 |X_{m}| \ge \frac12 \sum_{k=m+1}^\infty |b_k-b_{k-1}|, \end{align*} $$
$$ \begin{align*} & \frac32 \sum_{k=m+1}^\infty |X_k| +\frac12 |X_{m}| \ge \frac12 \sum_{k=m+1}^\infty |b_k-b_{k-1}|, \end{align*} $$
which yields
 $$ \begin{align*} & \| f \chi_{\bigcup_{j=m}^n B_j}\|_{L_1} = \sum_{k=m}^\infty |X_k| \ge \sum_{k=m+1}^\infty |X_k| +\frac13|X_m| \ge \frac13 \sum_{k=m+1}^\infty |b_k-b_{k-1}| \end{align*} $$
$$ \begin{align*} & \| f \chi_{\bigcup_{j=m}^n B_j}\|_{L_1} = \sum_{k=m}^\infty |X_k| \ge \sum_{k=m+1}^\infty |X_k| +\frac13|X_m| \ge \frac13 \sum_{k=m+1}^\infty |b_k-b_{k-1}| \end{align*} $$
and proves equation (22).
Theorem 2.6 Semenov-Uksusov, [Reference Semenov and Uksusov34, Reference Semenov and Uksusov35]
Let
![]() $(a_I)_{I\in \mathcal {D}^+}$
be a collection of scalars and D be the associated Haar multiplier. Define
$(a_I)_{I\in \mathcal {D}^+}$
be a collection of scalars and D be the associated Haar multiplier. Define
 $$ \begin{align} {\left\vert\kern-0.25ex\left\vert\kern-0.25ex\left\vert D \right\vert\kern-0.25ex\right\vert\kern-0.25ex\right\vert} = \sup\Big(\sum_{k=1}^\infty\big |a_{I_k} - a_{I_{k-1}}\big|+\lim_k\big|a_{I_k}\big|\Big), \end{align} $$
$$ \begin{align} {\left\vert\kern-0.25ex\left\vert\kern-0.25ex\left\vert D \right\vert\kern-0.25ex\right\vert\kern-0.25ex\right\vert} = \sup\Big(\sum_{k=1}^\infty\big |a_{I_k} - a_{I_{k-1}}\big|+\lim_k\big|a_{I_k}\big|\Big), \end{align} $$
where the supremum is taken over all
![]() $(I_k)_{k=0}^\infty \in [\mathcal {D}^+]$
. Then D is bounded (and thus extends to a bounded linear operator on
$(I_k)_{k=0}^\infty \in [\mathcal {D}^+]$
. Then D is bounded (and thus extends to a bounded linear operator on
![]() $L_1(X)$
) if and only if
$L_1(X)$
) if and only if
![]() ${\left \vert \kern -0.25ex\left \vert \kern -0.25ex\left \vert D \right \vert \kern -0.25ex\right \vert \kern -0.25ex\right \vert }<\infty $
. More precisely,
${\left \vert \kern -0.25ex\left \vert \kern -0.25ex\left \vert D \right \vert \kern -0.25ex\right \vert \kern -0.25ex\right \vert }<\infty $
. More precisely,
Proof. By equation (19), D is always well defined on the linear span of the set
![]() $\mathcal {X} = \{|I|^{-1}\chi _I:I\in \mathcal {D}\}$
. In fact, the closed convex symmetric hull of
$\mathcal {X} = \{|I|^{-1}\chi _I:I\in \mathcal {D}\}$
. In fact, the closed convex symmetric hull of
![]() $\mathcal {X}$
is the unit ball of
$\mathcal {X}$
is the unit ball of
![]() $L_1$
. We deduce that
$L_1$
. We deduce that
![]() $\|D\| = \sup \{\|Df\|:f\in \mathcal {X}\}$
, under the convention that
$\|D\| = \sup \{\|Df\|:f\in \mathcal {X}\}$
, under the convention that
![]() $\|D\| = \infty $
if and only if D is unbounded. Fix
$\|D\| = \infty $
if and only if D is unbounded. Fix
![]() $f = |I|^{-1}\chi _I\in \mathcal {X}$
. Use equation (19) to write
$f = |I|^{-1}\chi _I\in \mathcal {X}$
. Use equation (19) to write
 $$\begin{align*}f = |I_{k_0}|^{-1}\chi_{I_{k_0}} = \sum_{k=0}^{k_0-1}\theta_k|I_k|^{-1}h_{I_k},\ that is,\ Df = \sum_{k=0}^{k_0-1}a_k\theta_k|I_k|^{-1}h_{I_k}.\end{align*}$$
$$\begin{align*}f = |I_{k_0}|^{-1}\chi_{I_{k_0}} = \sum_{k=0}^{k_0-1}\theta_k|I_k|^{-1}h_{I_k},\ that is,\ Df = \sum_{k=0}^{k_0-1}a_k\theta_k|I_k|^{-1}h_{I_k}.\end{align*}$$
Extend
![]() $(I_k)_{k=0}^{k_0}$
to a branch
$(I_k)_{k=0}^{k_0}$
to a branch
![]() $(I_k)_{k=0}^\infty $
. By equation (21), we have
$(I_k)_{k=0}^\infty $
. By equation (21), we have
 $$ \begin{align} \frac{1}{3}\big(\sum_{k=1}^{k_0-1}|a_{I_k} - a_{I_{k-1}}| + |a_{I_{k_0-1}}|\big) \leq \|Df\|_{L_1} \leq \sum_{k=1}^{k_0-1}|a_{I_k} - a_{I_{k-1}}| + |a_{I_{k_0-1}}|. \end{align} $$
$$ \begin{align} \frac{1}{3}\big(\sum_{k=1}^{k_0-1}|a_{I_k} - a_{I_{k-1}}| + |a_{I_{k_0-1}}|\big) \leq \|Df\|_{L_1} \leq \sum_{k=1}^{k_0-1}|a_{I_k} - a_{I_{k-1}}| + |a_{I_{k_0-1}}|. \end{align} $$
By the triangle inequality,
![]() $\|Df\|_{L_1} \leq \sum _{k=1}^{\infty }|a_{I_k} - a_{I_{k-1}}| + \lim _k|a_{I_{k}}| \leq {\left \vert \kern -0.25ex\left \vert \kern -0.25ex\left \vert D \right \vert \kern -0.25ex\right \vert \kern -0.25ex\right \vert }$
. The lower bound is achieved by taking in equation (27) all
$\|Df\|_{L_1} \leq \sum _{k=1}^{\infty }|a_{I_k} - a_{I_{k-1}}| + \lim _k|a_{I_{k}}| \leq {\left \vert \kern -0.25ex\left \vert \kern -0.25ex\left \vert D \right \vert \kern -0.25ex\right \vert \kern -0.25ex\right \vert }$
. The lower bound is achieved by taking in equation (27) all
![]() $f\in \mathcal {X}$
.
$f\in \mathcal {X}$
.
The following special type of Haar multiplier will appear in the sequel.
Example 2.7. Let
![]() $\mathscr {A}\subset [\mathcal {D}^+]$
be a nonempty set, and define the set
$\mathscr {A}\subset [\mathcal {D}^+]$
be a nonempty set, and define the set
![]() $\mathcal {A} = \cup _{k_0=0}^\infty \{I_{k_0}:(I_k)_{k=0}^\infty \in \mathscr {A}\}\subset \mathcal {D}^+$
. Let
$\mathcal {A} = \cup _{k_0=0}^\infty \{I_{k_0}:(I_k)_{k=0}^\infty \in \mathscr {A}\}\subset \mathcal {D}^+$
. Let
![]() $P_{\mathscr {A}}$
denote the Haar multiplier that has entries
$P_{\mathscr {A}}$
denote the Haar multiplier that has entries
![]() $a_I = 1$
for
$a_I = 1$
for
![]() $I\in \mathcal {A}$
and
$I\in \mathcal {A}$
and
![]() $a_I = 0$
otherwise. Then by Theorem 2.6,
$a_I = 0$
otherwise. Then by Theorem 2.6,
![]() $\|P_{\mathscr {A}}\|\leq {\left \vert \kern -0.25ex\left \vert \kern -0.25ex\left \vert P_{\mathscr {A}} \right \vert \kern -0.25ex\right \vert \kern -0.25ex\right \vert } = 1$
, and therefore
$\|P_{\mathscr {A}}\|\leq {\left \vert \kern -0.25ex\left \vert \kern -0.25ex\left \vert P_{\mathscr {A}} \right \vert \kern -0.25ex\right \vert \kern -0.25ex\right \vert } = 1$
, and therefore
![]() $P_{\mathscr {A}}$
defines a norm-one projection onto
$P_{\mathscr {A}}$
defines a norm-one projection onto
![]() $Y_{\mathscr {A}} = \overline {\langle \{h_I:I\in \mathcal {A}\}\rangle }$
.
$Y_{\mathscr {A}} = \overline {\langle \{h_I:I\in \mathcal {A}\}\rangle }$
.
The following elementary remark will be useful eventually.
Remark 2.8. Let
![]() $\mathscr {A}$
be a nonempty closed subset of
$\mathscr {A}$
be a nonempty closed subset of
![]() $[\mathcal {D}^+]$
and
$[\mathcal {D}^+]$
and
![]() $\mathcal {A} = \cup _{k_0=0}^\infty \{I_{k_0}:(I_k)_{k=0}^\infty \in \mathscr {A}\}$
. Let D be a Haar multiplier with entries that are zero outside
$\mathcal {A} = \cup _{k_0=0}^\infty \{I_{k_0}:(I_k)_{k=0}^\infty \in \mathscr {A}\}$
. Let D be a Haar multiplier with entries that are zero outside
![]() $\mathcal {A}$
. Then
$\mathcal {A}$
. Then
 $$\begin{align*}{\left\vert\kern-0.25ex\left\vert\kern-0.25ex\left\vert D \right\vert\kern-0.25ex\right\vert\kern-0.25ex\right\vert} = \sup_{(I_k)_{k=0}^\infty\in\mathscr{A}}(\sum_{k=1}^\infty|a_{I_k}-a_{k-1}| + \lim_k|a_{I_k}|).\end{align*}$$
$$\begin{align*}{\left\vert\kern-0.25ex\left\vert\kern-0.25ex\left\vert D \right\vert\kern-0.25ex\right\vert\kern-0.25ex\right\vert} = \sup_{(I_k)_{k=0}^\infty\in\mathscr{A}}(\sum_{k=1}^\infty|a_{I_k}-a_{k-1}| + \lim_k|a_{I_k}|).\end{align*}$$
Haar multipliers provide a short path to a proof of the fact that every operator on
![]() $L_1$
is an approximate 1-projectional factor of a scalar operator, which in turn yields Enflo’s theorem [Reference Maurey26] that
$L_1$
is an approximate 1-projectional factor of a scalar operator, which in turn yields Enflo’s theorem [Reference Maurey26] that
![]() $L_1$
is primary.
$L_1$
is primary.
Theorem 2.9. The following are true in the space
![]() $L_1$
.
$L_1$
.
-
(i) Let
 $D:L_1\to L_1$
be a bounded Haar multiplier. For every
$D:L_1\to L_1$
be a bounded Haar multiplier. For every
 $\varepsilon>0$
, D is a 1-projectional factor with error
$\varepsilon>0$
, D is a 1-projectional factor with error
 $\varepsilon $
of a scalar operator.
$\varepsilon $
of a scalar operator. -
(ii) Let
 $T:L_1\to L_1$
be a bounded linear operator. For every
$T:L_1\to L_1$
be a bounded linear operator. For every
 $\varepsilon>0$
, T is a 1-projectional factor with error
$\varepsilon>0$
, T is a 1-projectional factor with error
 $\varepsilon $
of a bounded Haar multiplier
$\varepsilon $
of a bounded Haar multiplier
 $D:L_1\to L_1$
.
$D:L_1\to L_1$
.
In particular, for every
![]() $\varepsilon>0$
, every bounded linear operator
$\varepsilon>0$
, every bounded linear operator
![]() $T:L_1\to L_1$
is a 1-projectional factor with error
$T:L_1\to L_1$
is a 1-projectional factor with error
![]() $\varepsilon $
of a scalar operator.
$\varepsilon $
of a scalar operator.
We wish to provide a sketch of the proof of the above. First, we will use it at the end of the paper; and second, it provides an introduction to the basis of the methods used in the paper. Now, and numerous times in the sequel, we require the following notation and definition.
Notation. For every disjoint collection
![]() $\Delta $
of
$\Delta $
of
![]() $\mathcal {D}^+$
and
$\mathcal {D}^+$
and
![]() $\theta \in \{-1,1\}^\Delta $
, we denote
$\theta \in \{-1,1\}^\Delta $
, we denote
![]() $h_\Delta ^\theta = \sum _{J\in \Delta }\theta _Jh_J$
. If
$h_\Delta ^\theta = \sum _{J\in \Delta }\theta _Jh_J$
. If
![]() $\theta _J = 1$
for all
$\theta _J = 1$
for all
![]() $J\in \Delta $
, we write
$J\in \Delta $
, we write
![]() $h_\Delta = \sum _{j\in \Delta }h_J$
. For a finite disjoint collection
$h_\Delta = \sum _{j\in \Delta }h_J$
. For a finite disjoint collection
![]() $\Delta $
of
$\Delta $
of
![]() $\mathcal {D}$
, we denote
$\mathcal {D}$
, we denote
![]() $\Delta ^* = \cup \{I:I\in \Delta \}$
.
$\Delta ^* = \cup \{I:I\in \Delta \}$
.
Definition 2.10. A faithful Haar system is a collection
![]() $(\tilde h_I)_{I\in \mathcal {D}^+}$
so that for each
$(\tilde h_I)_{I\in \mathcal {D}^+}$
so that for each
![]() $I\in \mathcal {D}^+$
, the function
$I\in \mathcal {D}^+$
, the function
![]() $\tilde h_I$
is of the form
$\tilde h_I$
is of the form
![]() $\tilde h_I = h_{\Delta _I}^{\theta _I}$
, for some finite disjoint collection
$\tilde h_I = h_{\Delta _I}^{\theta _I}$
, for some finite disjoint collection
![]() $\Delta _I$
of
$\Delta _I$
of
![]() $\mathcal {D}$
, and so that
$\mathcal {D}$
, and so that
-
(i)
 $\Delta _\emptyset ^* = \Delta _{[0,1)}^* = [0,1)$
, and for each
$\Delta _\emptyset ^* = \Delta _{[0,1)}^* = [0,1)$
, and for each
 $I\in \mathcal {D}$
, we have
$I\in \mathcal {D}$
, we have
 $|\Delta _I| = |I|$
,
$|\Delta _I| = |I|$
, -
(ii) for every
 $I\in \mathcal {D}$
, we have that
$I\in \mathcal {D}$
, we have that
 $\Delta _{I^+}^* = [\tilde h_\emptyset \tilde h_I = 1]$
and
$\Delta _{I^+}^* = [\tilde h_\emptyset \tilde h_I = 1]$
and
 $\Delta _{I^-}^* = [\tilde h_\emptyset \tilde h_I = -1]$
.
$\Delta _{I^-}^* = [\tilde h_\emptyset \tilde h_I = -1]$
.
Remark 2.11. It is immediate that
![]() $(\tilde h_\emptyset \tilde h_I)_{I\in \mathcal {D}^+}$
is distributionally equivalent to
$(\tilde h_\emptyset \tilde h_I)_{I\in \mathcal {D}^+}$
is distributionally equivalent to
![]() $(h_I)_{I\in \mathcal {D}^+}$
. Therefore,
$(h_I)_{I\in \mathcal {D}^+}$
. Therefore,
![]() $(\tilde h_I)_{I\in \mathcal {D}^+}$
is isometrically equivalent to
$(\tilde h_I)_{I\in \mathcal {D}^+}$
is isometrically equivalent to
![]() $(h_I)_{I\in \mathcal {D}^+}$
, both in
$(h_I)_{I\in \mathcal {D}^+}$
, both in
![]() $L_1$
and in
$L_1$
and in
![]() $L_\infty $
. In particular,
$L_\infty $
. In particular,
defines a norm-one projection onto a subspace Z of
![]() $L_1$
that is isometrically isomorphic to
$L_1$
that is isometrically isomorphic to
![]() $L_1$
. Note that unless
$L_1$
. Note that unless
![]() $h_\emptyset = 1$
, P is not a conditional expectation as
$h_\emptyset = 1$
, P is not a conditional expectation as
![]() $P\chi _{[0,1)} = 0$
. Instead, it is of the form
$P\chi _{[0,1)} = 0$
. Instead, it is of the form
![]() $Pf = \tilde h_\emptyset E(\tilde h_\emptyset f|\Sigma )$
, where
$Pf = \tilde h_\emptyset E(\tilde h_\emptyset f|\Sigma )$
, where
![]() $\Sigma = \sigma (\tilde h_\emptyset \tilde h_I)_{I\in \mathcal {D}^+}$
. Since
$\Sigma = \sigma (\tilde h_\emptyset \tilde h_I)_{I\in \mathcal {D}^+}$
. Since
![]() $\tilde h_\emptyset $
is not
$\tilde h_\emptyset $
is not
![]() $\Sigma $
-measurable, it cannot be eliminated. The advantage of the notion of a faithful Haar system is that one can be constructed in every tail of the Haar system. The drawback is that it causes a slight notational burden when having to adjust for the initial function
$\Sigma $
-measurable, it cannot be eliminated. The advantage of the notion of a faithful Haar system is that one can be constructed in every tail of the Haar system. The drawback is that it causes a slight notational burden when having to adjust for the initial function
![]() $\tilde h_\emptyset $
in several situations.
$\tilde h_\emptyset $
in several situations.
We will several times recursively construct faithful Haar systems
![]() $(\tilde h_I)_{I\in \mathcal {D}^+}$
, which means we first choose
$(\tilde h_I)_{I\in \mathcal {D}^+}$
, which means we first choose
![]() $\tilde h_\emptyset $
, second
$\tilde h_\emptyset $
, second
![]() $\tilde h_{[0,1)}$
and then
$\tilde h_{[0,1)}$
and then
![]() $\tilde h_I$
,
$\tilde h_I$
,
![]() $I\in \mathcal D$
, assuming that
$I\in \mathcal D$
, assuming that
![]() $\tilde h_J$
was chosen for all
$\tilde h_J$
was chosen for all
![]() $J\in \mathcal D ^+$
with
$J\in \mathcal D ^+$
with
![]() $\iota (J) < \iota (I)$
.
$\iota (J) < \iota (I)$
.
Proof of Theorem 2.9
Let us sketch the proof of the first statement. Let
![]() $(a_I)_{I\in \mathcal {D}^+}$
be the entries of D. For every
$(a_I)_{I\in \mathcal {D}^+}$
be the entries of D. For every
![]() $I\in \mathcal {D}$
, denote by
$I\in \mathcal {D}$
, denote by
![]() $Q_I$
the Haar multiplier that has entries 1 for all
$Q_I$
the Haar multiplier that has entries 1 for all
![]() $J\subset I$
and zero for all others. Then
$J\subset I$
and zero for all others. Then
![]() ${\left \vert \kern -0.25ex\left \vert \kern -0.25ex\left \vert Q_I \right \vert \kern -0.25ex\right \vert \kern -0.25ex\right \vert } = 1$
. First, note that for every
${\left \vert \kern -0.25ex\left \vert \kern -0.25ex\left \vert Q_I \right \vert \kern -0.25ex\right \vert \kern -0.25ex\right \vert } = 1$
. First, note that for every
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $I_0\in \mathcal {D}^+$
so that
$I_0\in \mathcal {D}^+$
so that
![]() ${\left \vert \kern -0.25ex\left \vert \kern -0.25ex\left \vert DQ_{I_0} - a_{I_0}Q_{I_0} \right \vert \kern -0.25ex\right \vert \kern -0.25ex\right \vert }\leq \varepsilon $
. Otherwise, we could easily deduce
${\left \vert \kern -0.25ex\left \vert \kern -0.25ex\left \vert DQ_{I_0} - a_{I_0}Q_{I_0} \right \vert \kern -0.25ex\right \vert \kern -0.25ex\right \vert }\leq \varepsilon $
. Otherwise, we could easily deduce
![]() ${\left \vert \kern -0.25ex\left \vert \kern -0.25ex\left \vert D \right \vert \kern -0.25ex\right \vert \kern -0.25ex\right \vert } = \infty $
. Construct a dilated and renormalised faithful Haar system
${\left \vert \kern -0.25ex\left \vert \kern -0.25ex\left \vert D \right \vert \kern -0.25ex\right \vert \kern -0.25ex\right \vert } = \infty $
. Construct a dilated and renormalised faithful Haar system
![]() $(\tilde h_I)_{I\in \mathcal {D}^+}$
with closed linear span Z in the range of
$(\tilde h_I)_{I\in \mathcal {D}^+}$
with closed linear span Z in the range of
![]() $Q_{I_0}$
, and let
$Q_{I_0}$
, and let
![]() $P:L_1\to Z$
be the corresponding norm-one projection and
$P:L_1\to Z$
be the corresponding norm-one projection and
![]() $A:L_1\to Z$
be an onto isometry. Then
$A:L_1\to Z$
be an onto isometry. Then
![]() $\|A^{-1}PDA - a_{I_0}I\| \leq \varepsilon $
.
$\|A^{-1}PDA - a_{I_0}I\| \leq \varepsilon $
.
For the second part, we will use that the Rademacher sequence
![]() $(r_n)_n$
(i.e.,
$(r_n)_n$
(i.e.,
![]() $r_n = \sum _{L\in \mathcal {D}_n}h_L$
, for
$r_n = \sum _{L\in \mathcal {D}_n}h_L$
, for
![]() $n\in \mathbb {N}$
)) is weakly null in
$n\in \mathbb {N}$
)) is weakly null in
![]() $L_1$
and
$L_1$
and
![]() $w^*$
-null in
$w^*$
-null in
![]() $(L_1)^* \equiv L_\infty $
. Using this fact, we inductively construct a faithful Haar system
$(L_1)^* \equiv L_\infty $
. Using this fact, we inductively construct a faithful Haar system
![]() $(\tilde h_I)_{I\in \mathcal {D}^+}$
so that for each
$(\tilde h_I)_{I\in \mathcal {D}^+}$
so that for each
![]() $I\neq J$
, we have
$I\neq J$
, we have
where
![]() $(\varepsilon _{(I,J)})_{(I,J)\in \mathcal {D}^+}$
is a prechosen collection of positive real numbers with
$(\varepsilon _{(I,J)})_{(I,J)\in \mathcal {D}^+}$
is a prechosen collection of positive real numbers with
![]() $\sum \varepsilon _{(I,J)} \leq \varepsilon $
. This is done as follows. If we have chosen
$\sum \varepsilon _{(I,J)} \leq \varepsilon $
. This is done as follows. If we have chosen
![]() $\tilde h_I$
for
$\tilde h_I$
for
![]() $\iota (I) = 1,\ldots ,k-1$
. Let
$\iota (I) = 1,\ldots ,k-1$
. Let
![]() $I\in \mathcal {D}^+$
with
$I\in \mathcal {D}^+$
with
![]() $\iota (I) = k$
, and let
$\iota (I) = k$
, and let
![]() $I_0$
be the predecessor of I: that is, either
$I_0$
be the predecessor of I: that is, either
![]() $I = I_0^+$
or
$I = I_0^+$
or
![]() $I = I_0^-$
. Let us assume
$I = I_0^-$
. Let us assume
![]() $I = I_0^+$
. We then choose the next function
$I = I_0^+$
. We then choose the next function
![]() $\tilde h_I$
among the terms of a Rademacher sequence with support
$\tilde h_I$
among the terms of a Rademacher sequence with support
![]() $[\tilde h_\emptyset \tilde h_{I_0} = 1]$
. Denote by Z the closed linear span of
$[\tilde h_\emptyset \tilde h_{I_0} = 1]$
. Denote by Z the closed linear span of
![]() $(\tilde h_I)_{I\in \mathcal {D}^+}$
, and take the canonical projection
$(\tilde h_I)_{I\in \mathcal {D}^+}$
, and take the canonical projection
![]() $P:L_1\to Z$
as well as the onto isometry
$P:L_1\to Z$
as well as the onto isometry
![]() $A:L_1\to Z$
given by
$A:L_1\to Z$
given by
![]() $A h_I = \tilde h_I$
. Consider the operator
$A h_I = \tilde h_I$
. Consider the operator
![]() $S=A^{-1}PTA:L_1\to L_1$
, and note that for all
$S=A^{-1}PTA:L_1\to L_1$
, and note that for all
![]() $I\neq J$
, we have
$I\neq J$
, we have
![]() $|\langle h_I, S(|J|^{-1}h_J) \rangle | = |\langle \tilde h_I, T(|J|^{-1}\tilde h_J )\rangle | \leq \varepsilon _{(I,J)}$
. It follows that the entries
$|\langle h_I, S(|J|^{-1}h_J) \rangle | = |\langle \tilde h_I, T(|J|^{-1}\tilde h_J )\rangle | \leq \varepsilon _{(I,J)}$
. It follows that the entries
![]() $a_I = \langle h_I, S(|I|^{-1}h_I )\rangle $
define a bounded Haar multiplier D and
$a_I = \langle h_I, S(|I|^{-1}h_I )\rangle $
define a bounded Haar multiplier D and
![]() $\|S - D\| \leq \varepsilon $
: that is, T is a 1-projectional factor with error
$\|S - D\| \leq \varepsilon $
: that is, T is a 1-projectional factor with error
![]() $\varepsilon $
of D.
$\varepsilon $
of D.
2.4 Haar system spaces
We define Haar system spaces. These are Banach spaces of scalar function generated by the Haar system in which two functions with the same distribution have the same norm. This abstraction does not impose any notational burden on the proof of the main result. The only difference to the case
![]() $X= L_p$
is the normalisation of the Haar basis. Properties such as unconditionality of the Haar system and reflexivity of
$X= L_p$
is the normalisation of the Haar basis. Properties such as unconditionality of the Haar system and reflexivity of
![]() $L_p$
are never deployed.
$L_p$
are never deployed.
Definition 2.12. A Haar system space X is the completion of
![]() $Z = \langle \{ h_L:L\in \mathcal {D}^+\}\rangle = \langle \{\chi _I:I\in \mathcal {D}\}\rangle $
under a norm
$Z = \langle \{ h_L:L\in \mathcal {D}^+\}\rangle = \langle \{\chi _I:I\in \mathcal {D}\}\rangle $
under a norm
![]() $\|\cdot \|$
that satisfies the following properties:
$\|\cdot \|$
that satisfies the following properties:
-
(i) If f, g are in Z and
 $|f|$
,
$|f|$
,
 $|g|$
have the same distribution, then
$|g|$
have the same distribution, then
 $\|f\| = \|g\|$
.
$\|f\| = \|g\|$
. -
(ii)
 $\|\chi _{[0,1)}\| = 1$
.
$\|\chi _{[0,1)}\| = 1$
.
We denote the class of Haar system spaces by
![]() $\mathcal H$
.
$\mathcal H$
.
Obviously, property (ii) may be achieved by scaling the norm of a space that satisfies (i). We include it anyway for notational convenience.
An important class of spaces that satisfy Definition 2.12, according to [Reference Lindenstrauss and Tzafriri25, Proposition 2.c.1], are separable rearrangement-invariant function spaces on
![]() $[0,1]$
. Recall that a (nonzero) Banach space Y of measurable scalar functions on
$[0,1]$
. Recall that a (nonzero) Banach space Y of measurable scalar functions on
![]() $[0,1)$
is called rearrangement invariant (or, as in [Reference Rodin and Semyonov31], symmetric) if the following conditions hold true. First, whenever
$[0,1)$
is called rearrangement invariant (or, as in [Reference Rodin and Semyonov31], symmetric) if the following conditions hold true. First, whenever
![]() $f\in Y$
and g is a measurable function with
$f\in Y$
and g is a measurable function with
![]() $|g|\leq |f|$
a.e., then
$|g|\leq |f|$
a.e., then
![]() $g\in Y$
and
$g\in Y$
and
![]() $\|g\|_Y \leq \|f\|_Y$
. Second, if
$\|g\|_Y \leq \|f\|_Y$
. Second, if
![]() $u,v$
are in Y and they have the same distribution, then
$u,v$
are in Y and they have the same distribution, then
![]() $\|u\|_Y = \|v\|_Y$
.
$\|u\|_Y = \|v\|_Y$
.
The following properties of a Haar system space X follow from elementary arguments. For completeness, we provide the proofs.
Proposition 2.13. Let X be a Haar system space.
-
(a) For every
 $f\in Z = \langle \{\chi _I:I\in \mathcal {D}\}\rangle $
, we have
$f\in Z = \langle \{\chi _I:I\in \mathcal {D}\}\rangle $
, we have
 $\|f\|_{L_1}\leq \|f\|\leq \|f\|_{L_\infty }$
. Therefore, X can be naturally identified with a space of measurable scalar functions on
$\|f\|_{L_1}\leq \|f\|\leq \|f\|_{L_\infty }$
. Therefore, X can be naturally identified with a space of measurable scalar functions on
 $[0,1)$
and
$[0,1)$
and
 ${\overline Z^{\|\cdot \|_{L_\infty }}} \subset X \subset {L_1}$
.
${\overline Z^{\|\cdot \|_{L_\infty }}} \subset X \subset {L_1}$
. -
(b)
 $Z = \langle \{\chi _I:I\in \mathcal {D}\}\rangle $
naturally coincides with a subspace of
$Z = \langle \{\chi _I:I\in \mathcal {D}\}\rangle $
naturally coincides with a subspace of
 $X^*$
, and its closure
$X^*$
, and its closure
 $\overline Z$
in
$\overline Z$
in
 $X^*$
is also a Haar system space.
$X^*$
is also a Haar system space. -
(c) The Haar system, in the usual linear order, is a monotone Schauder basis of X.
-
(d) For a finite union A of elements of
 $\mathcal {D}$
, we put
$\mathcal {D}$
, we put
 $\mu _A = \|\chi _A\|^{-1}_X$
and
$\mu _A = \|\chi _A\|^{-1}_X$
and
 $\nu _A = \|\chi _A\|^{-1}_{X^*}$
. Then
$\nu _A = \|\chi _A\|^{-1}_{X^*}$
. Then
 $\mu _A\nu _A = |A|^{-1}$
. In particular,
$\mu _A\nu _A = |A|^{-1}$
. In particular,
 $(\nu _Lh_L,\mu _Lh_L)_{L\in \mathcal {D}^+}$
is a biorthogonal system in
$(\nu _Lh_L,\mu _Lh_L)_{L\in \mathcal {D}^+}$
is a biorthogonal system in
 $X^*\times X$
.
$X^*\times X$
. -
(e) A faithful Haar system
 $(\widehat h_L)_{L\in \mathcal {D}^+}$
is isometrically equivalent to
$(\widehat h_L)_{L\in \mathcal {D}^+}$
is isometrically equivalent to
 $(h_L)_{L\in \mathcal {D}^+}$
. In particular,
$(h_L)_{L\in \mathcal {D}^+}$
. In particular,
 $Pf = \sum _{L\in \mathcal {D}^+}\langle \nu _L\widehat h_L,f \rangle \mu _L\widehat h_L$
defines a norm-one projection onto a subspace of X that is isometrically isomorphic to X.
$Pf = \sum _{L\in \mathcal {D}^+}\langle \nu _L\widehat h_L,f \rangle \mu _L\widehat h_L$
defines a norm-one projection onto a subspace of X that is isometrically isomorphic to X.
Proof. By the first condition in Definition 2.12, we have
for all
![]() $n\in \mathbb {N}$
, all permutations
$n\in \mathbb {N}$
, all permutations
![]() $\pi $
on
$\pi $
on
![]() $\mathcal D_n$
and all scalar families
$\mathcal D_n$
and all scalar families
![]() $(a_I:I\in \mathcal D_n)$
.
$(a_I:I\in \mathcal D_n)$
.
To show the first inequality in (a), let
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
![]() $f=\sum _{I\in \mathcal D_n} a_I \chi _I\in Z$
, and let
$f=\sum _{I\in \mathcal D_n} a_I \chi _I\in Z$
, and let
![]() $\pi :\mathcal D_n\to \mathcal D_n $
, be cyclic (i.e.,
$\pi :\mathcal D_n\to \mathcal D_n $
, be cyclic (i.e.,
![]() $\{\pi ^r(I):r=1,2\ldots ,2^n\}=\mathcal D_n$
for
$\{\pi ^r(I):r=1,2\ldots ,2^n\}=\mathcal D_n$
for
![]() $I\in \mathcal D_n$
). Then
$I\in \mathcal D_n$
). Then
 $$ \begin{align*}\|f\|=\big\| |f|\big\| \ge \frac1{2^n} \Big\|\sum_{r=1}^{2^n} \sum_{I\in \mathcal D_n} |a_I| \chi_{\pi^r(I)}\Big\|=\frac1{2^n}\Big|\sum_{I\in \mathcal D_n} |a_I|\Big|=\|f\|_{L_1}.\end{align*} $$
$$ \begin{align*}\|f\|=\big\| |f|\big\| \ge \frac1{2^n} \Big\|\sum_{r=1}^{2^n} \sum_{I\in \mathcal D_n} |a_I| \chi_{\pi^r(I)}\Big\|=\frac1{2^n}\Big|\sum_{I\in \mathcal D_n} |a_I|\Big|=\|f\|_{L_1}.\end{align*} $$
The second inequality in (a) follows from the observation that for each
![]() $n\in \mathbb {N}$
, the family
$n\in \mathbb {N}$
, the family
![]() $(\chi _I: I \in \mathcal D_n)$
is
$(\chi _I: I \in \mathcal D_n)$
is
![]() $1$
-unconditional.
$1$
-unconditional.
We identify each
![]() $g\in Z$
with the bounded functional
$g\in Z$
with the bounded functional
![]() $x^*_g$
, defined by
$x^*_g$
, defined by
![]() $x^*_g(f)=\int _0^1 f g$
, and we denote the dual norm by
$x^*_g(f)=\int _0^1 f g$
, and we denote the dual norm by
![]() $\|\cdot \|_{*}$
. From this representation it is clear that
$\|\cdot \|_{*}$
. From this representation it is clear that
![]() $\|\cdot \|_*$
also satisfies the first condition in Definition 2.12. Since
$\|\cdot \|_*$
also satisfies the first condition in Definition 2.12. Since
![]() $\|1_{[0,1)]}\|=1$
, and since for all
$\|1_{[0,1)]}\|=1$
, and since for all
![]() $f\in Z$
,
$f\in Z$
,
![]() $ \int f \le \|f\|_1\le \|f\|$
, we deduce that the second condition in Definition 2.12 holds true for the norm
$ \int f \le \|f\|_1\le \|f\|$
, we deduce that the second condition in Definition 2.12 holds true for the norm
![]() $\|\cdot \|_*$
.
$\|\cdot \|_*$
.
Let
![]() $(h_n)$
be the Haar basis linearly ordered in the usual way, meaning that if
$(h_n)$
be the Haar basis linearly ordered in the usual way, meaning that if
![]() $m<n$
, then either
$m<n$
, then either
![]() $\mathrm {supp}(h_n)\subset \mathrm {supp}(h_m)$
or
$\mathrm {supp}(h_n)\subset \mathrm {supp}(h_m)$
or
![]() $\mathrm {supp}(h_n)\cap \mathrm {supp}(h_m)=\emptyset $
. The claim of condition (c) follows from the fact that if
$\mathrm {supp}(h_n)\cap \mathrm {supp}(h_m)=\emptyset $
. The claim of condition (c) follows from the fact that if
![]() $f=\sum _{j=1}^n a_j h_j\in Z$
, then for any scalar
$f=\sum _{j=1}^n a_j h_j\in Z$
, then for any scalar
![]() $a_{n+1}$
, the absolute values of the functions
$a_{n+1}$
, the absolute values of the functions
![]() $f+a_{n+1} h_{n+1}$
and
$f+a_{n+1} h_{n+1}$
and
![]() $f-a_{n+1} h_{n+1}$
have the same distribution and their average is f.
$f-a_{n+1} h_{n+1}$
have the same distribution and their average is f.
Let
![]() $n\!\in \!\mathbb {N}$
and
$n\!\in \!\mathbb {N}$
and
![]() $I\!\in \!\mathcal D_n$
using for
$I\!\in \!\mathcal D_n$
using for
![]() $k\!>\!n$
cyclic permutations on
$k\!>\!n$
cyclic permutations on
![]() $\{ J\!\in \!\mathcal D_k, J\!\subset \!I\}$
. We deduce that
$\{ J\!\in \!\mathcal D_k, J\!\subset \!I\}$
. We deduce that
![]() $\sup _{f\in Z,\|f\|\le 1} \int _I f$
is attained for
$\sup _{f\in Z,\|f\|\le 1} \int _I f$
is attained for
![]() $f=\chi _I/\|\chi _I\|$
and thus
$f=\chi _I/\|\chi _I\|$
and thus
![]() $\|\chi _I\|\cdot \|\chi _I\|_*=2^{-n}$
. Since, second, for each n,
$\|\chi _I\|\cdot \|\chi _I\|_*=2^{-n}$
. Since, second, for each n,
![]() $(\chi _I: I \in \mathcal D_n)$
is an orthogonal family, we deduce (d).
$(\chi _I: I \in \mathcal D_n)$
is an orthogonal family, we deduce (d).
Since faithful Haar systems have the same joint distribution, we deduce the first part of (e). Since by (b), this is also true with respect to the dual norm, we deduce the second part of (e).
In different parts of the proof, we will require additional properties of Haar system spaces. The following class of Haar system spaces is the one for which we prove our main theorem.
Definition 2.14. We define
![]() $\mathcal H^*$
as the class of all Banach spaces X in
$\mathcal H^*$
as the class of all Banach spaces X in
![]() $\mathcal H$
satisfying
$\mathcal H$
satisfying
-
(II) the Rademacher sequence
 $(r_n)_n$
is not equivalent to the
$(r_n)_n$
is not equivalent to the
 $\ell _1$
-unit vector basis.
$\ell _1$
-unit vector basis.
We define
![]() $\mathcal H^{**}$
as the class of all Banach spaces X in
$\mathcal H^{**}$
as the class of all Banach spaces X in
![]() $\mathcal H$
satisfying
$\mathcal H$
satisfying
-
(II) no subsequence of the X-normalised Haar system
 $(\mu _Lh_L)_{L\in \mathcal {D}^+}$
is equivalent to the
$(\mu _Lh_L)_{L\in \mathcal {D}^+}$
is equivalent to the
 $\ell _1$
-unit vector basis.
$\ell _1$
-unit vector basis.
Remark 2.15. Examples of Haar system spaces that satisfy (
![]() $\star $
) and (
$\star $
) and (
![]() $\star \star $
) are separable reflexive r.i. spaces.
$\star \star $
) are separable reflexive r.i. spaces.
We note and will use several times that (
![]() $\star $
) for Haar system spaces is equivalent, with the condition that the Rademacher sequence
$\star $
) for Haar system spaces is equivalent, with the condition that the Rademacher sequence
![]() $(r_n)$
is weakly null. To see this, first note that for any
$(r_n)$
is weakly null. To see this, first note that for any
![]() $(a_n)\in c_{00}$
, any
$(a_n)\in c_{00}$
, any
![]() $\sigma =(\sigma _n)\subset \{\pm 1\}$
and permutation
$\sigma =(\sigma _n)\subset \{\pm 1\}$
and permutation
![]() $\pi $
on
$\pi $
on
![]() $\mathbb {N}$
, the distribution of
$\mathbb {N}$
, the distribution of
![]() $\sum _{n\in \mathbb {N}} a_n\sigma _n r_{\pi (n)}$
, does not depend on
$\sum _{n\in \mathbb {N}} a_n\sigma _n r_{\pi (n)}$
, does not depend on
![]() $\sigma $
on
$\sigma $
on
![]() $\pi $
. It follows that
$\pi $
. It follows that
![]() $(r_n)$
is a symmetric basic sequence in X. This implies that either
$(r_n)$
is a symmetric basic sequence in X. This implies that either
![]() $r_n$
is equivalent to the
$r_n$
is equivalent to the
![]() $\ell _1$
unit vector basis or it is weakly null in X. Indeed, if it is not equivalent to the unit vector basis of
$\ell _1$
unit vector basis or it is weakly null in X. Indeed, if it is not equivalent to the unit vector basis of
![]() $\ell _1$
, and by symmetry no subsequence is equivalent to the
$\ell _1$
, and by symmetry no subsequence is equivalent to the
![]() $\ell _1$
unit vector basis, it must by Rosenthal’s
$\ell _1$
unit vector basis, it must by Rosenthal’s
![]() $\ell _1$
Theorem have weakly Cauchy subsequence; and thus, for some subsequence
$\ell _1$
Theorem have weakly Cauchy subsequence; and thus, for some subsequence
![]() $(n_k)\subset \mathbb {N}$
, the sequence
$(n_k)\subset \mathbb {N}$
, the sequence
![]() $(r_{n_{2k}}- r_{n_{2k-1}}:k\in \mathbb {N})$
is weakly null. But then the sequence
$(r_{n_{2k}}- r_{n_{2k-1}}:k\in \mathbb {N})$
is weakly null. But then the sequence
![]() $(r_{n_{2k}}+ r_{n_{2k-1}}:k\in \mathbb {N})$
is also weakly null, and thus
$(r_{n_{2k}}+ r_{n_{2k-1}}:k\in \mathbb {N})$
is also weakly null, and thus
![]() $r_{n_{2k}}$
is weakly null and by symmetry
$r_{n_{2k}}$
is weakly null and by symmetry
![]() $(r_n)$
is weakly null.
$(r_n)$
is weakly null.
2.5 Complemented subspaces of
 ${L_1(X)}$
isomorphic to
${L_1(X)}$
isomorphic to
 $L_1(X)$
$L_1(X)$
Let E, F be Banach spaces. The projective tensor product of E and F is the completion of the algebraic tensor product
![]() $E\otimes F$
under the norm
$E\otimes F$
under the norm
 $$ \begin{align} \|u\| = \inf\Big\{\sum_{n=1}^N\|e_n\|\|f_n\|: u = \sum_{n=1}^Ne_n\otimes f_n\Big\}. \end{align} $$
$$ \begin{align} \|u\| = \inf\Big\{\sum_{n=1}^N\|e_n\|\|f_n\|: u = \sum_{n=1}^Ne_n\otimes f_n\Big\}. \end{align} $$
It is well known and follows from the definition of Bochner-Lebesque spaces that for any Banach space X,
![]() $L_1\otimes _\pi X\equiv L_1(X)$
via the identification
$L_1\otimes _\pi X\equiv L_1(X)$
via the identification
![]() $(f\otimes x)(s) = f(s)x$
. Then
$(f\otimes x)(s) = f(s)x$
. Then
![]() $L_\infty (X^*)$
canonically embeds into
$L_\infty (X^*)$
canonically embeds into
![]() $(L_1(X))^*$
via the identification
$(L_1(X))^*$
via the identification
![]() $\langle u,v\rangle = \int _0^1 \langle u(s),v(s)\rangle ds$
. Recall that by the definition of tensor norms, the projective tensor norm satisfies the following property we will use.
$\langle u,v\rangle = \int _0^1 \langle u(s),v(s)\rangle ds$
. Recall that by the definition of tensor norms, the projective tensor norm satisfies the following property we will use.
-
(•) For any pair of bounded linear operators
 $T:E\to E$
and
$T:E\to E$
and
 $S:F\to F$
, there exists a unique bounded linear operator
$S:F\to F$
, there exists a unique bounded linear operator
 $T\otimes S:E\otimes _\pi F\to E\otimes _\pi F$
with
$T\otimes S:E\otimes _\pi F\to E\otimes _\pi F$
with
 $(T\otimes S)(e\otimes f) = (Te)\otimes (Sf)$
and
$(T\otimes S)(e\otimes f) = (Te)\otimes (Sf)$
and
 $\|T\otimes S\| = \|T\|\|S\|$
.
$\|T\otimes S\| = \|T\|\|S\|$
.
The next standard statement explains one of the main features of the projective tensor product. For the sake of completeness, and because it is essential in this paper, we include the proof.
Proposition 2.16. Let Z be a subspace of
![]() $L_1$
that is isometrically isomorphic to
$L_1$
that is isometrically isomorphic to
![]() $L_1$
via
$L_1$
via
![]() $A:L_1\to Z$
and 1-complemented in
$A:L_1\to Z$
and 1-complemented in
![]() $L_1$
via
$L_1$
via
![]() $P:L_1\to Z$
. Let X be a Banach space, and let W be a subspace of X that is isometrically isomorphic to X via
$P:L_1\to Z$
. Let X be a Banach space, and let W be a subspace of X that is isometrically isomorphic to X via
![]() $B:X\to W$
and
$B:X\to W$
and
![]() $1$
-complemented in X via
$1$
-complemented in X via
![]() $Q:X\to W$
.
$Q:X\to W$
.
Then the space
![]() $Z(W) =\overline {Z\otimes W}^{L_1(X)}$
coincides with
$Z(W) =\overline {Z\otimes W}^{L_1(X)}$
coincides with
![]() $Z\otimes _\pi W$
and is isometrically isomorphic to
$Z\otimes _\pi W$
and is isometrically isomorphic to
![]() $L_1(X)$
via
$L_1(X)$
via
![]() $A\otimes B:L_1(X)\to Z(W)$
and 1-complemented in
$A\otimes B:L_1(X)\to Z(W)$
and 1-complemented in
![]() $L_1(X)$
via
$L_1(X)$
via
![]() $P\otimes Q:L_1(X)\to Z(W)$
.
$P\otimes Q:L_1(X)\to Z(W)$
.
Proof. It is immediate that
![]() $P\otimes Q$
is a norm-one projection onto
$P\otimes Q$
is a norm-one projection onto
![]() $Z(W)$
and that
$Z(W)$
and that
![]() $A\otimes B$
is a norm-one map with dense image. It also follows that
$A\otimes B$
is a norm-one map with dense image. It also follows that
![]() $A\otimes B$
is 1-1 on
$A\otimes B$
is 1-1 on
![]() $L_1\otimes X$
. One way to see this is to identify
$L_1\otimes X$
. One way to see this is to identify
![]() $L_1\otimes X$
and
$L_1\otimes X$
and
![]() $Z\otimes W$
with spaces of bilinear forms on
$Z\otimes W$
with spaces of bilinear forms on
![]() $(L_1)^*\times X^*$
and
$(L_1)^*\times X^*$
and
![]() $Z^*\times W^*$
, respectively. To conclude that
$Z^*\times W^*$
, respectively. To conclude that
![]() $A\otimes B$
is an isometry and that
$A\otimes B$
is an isometry and that
![]() $Z(W)=Z\otimes _{\pi } W$
, take u in
$Z(W)=Z\otimes _{\pi } W$
, take u in
![]() $L_1\otimes X$
. Note that
$L_1\otimes X$
. Note that
![]() $v:=(A\otimes B)(u)$
is in
$v:=(A\otimes B)(u)$
is in
![]() $Z\otimes W\subset L_1\otimes X$
, and write
$Z\otimes W\subset L_1\otimes X$
, and write
![]() $v = \sum _{i=1}^nf_i\otimes x_i$
, where
$v = \sum _{i=1}^nf_i\otimes x_i$
, where
![]() $f_1,\ldots ,f_n\in L_1$
and
$f_1,\ldots ,f_n\in L_1$
and
![]() $x_1,\ldots ,x_n\in X$
. We will see that
$x_1,\ldots ,x_n\in X$
. We will see that
![]() $\sum _{i=1}^n\|f_i\|\|x_i\| \geq \|u\|$
, which will imply the conclusion by the definition of
$\sum _{i=1}^n\|f_i\|\|x_i\| \geq \|u\|$
, which will imply the conclusion by the definition of
![]() $\|v\|$
. Indeed,
$\|v\|$
. Indeed,
![]() $v = (P\otimes Q)(v) = \sum _{i=1}^n(Pf_i)\otimes (Qx_i)$
and
$v = (P\otimes Q)(v) = \sum _{i=1}^n(Pf_i)\otimes (Qx_i)$
and
 $$ \begin{align*} \|v\| &\geq \sum_{i=1}^n\|Pf_i\|\|Qx_i\| = \sum_{i=1}^n\|A^{-1}Pf_i\|\|B^{-1}Qx_i\|\\ & \geq \big\|\underbrace{\sum_{i=1}^n\big(A^{-1}Pf_i\big)\otimes\big(B^{-1}Qx_i\big)}_{=:y}\big\|. \end{align*} $$
$$ \begin{align*} \|v\| &\geq \sum_{i=1}^n\|Pf_i\|\|Qx_i\| = \sum_{i=1}^n\|A^{-1}Pf_i\|\|B^{-1}Qx_i\|\\ & \geq \big\|\underbrace{\sum_{i=1}^n\big(A^{-1}Pf_i\big)\otimes\big(B^{-1}Qx_i\big)}_{=:y}\big\|. \end{align*} $$
It is immediate that
![]() $(A\otimes B)(y) = v$
and thus
$(A\otimes B)(y) = v$
and thus
![]() $y = u$
.
$y = u$
.
The following standard example will be used often to define projectional factors of an operator
![]() $T:L_1(X)\to L_1(X)$
.
$T:L_1(X)\to L_1(X)$
.
Example 2.17. Let
![]() $(\widetilde h_I)_{I\in \mathcal {D}^+}$
,
$(\widetilde h_I)_{I\in \mathcal {D}^+}$
,
![]() $(\widehat h_L)_{L\in \mathcal {D}^+}$
be a faithful Haar systems, and let X be a Haar system space. Take
$(\widehat h_L)_{L\in \mathcal {D}^+}$
be a faithful Haar systems, and let X be a Haar system space. Take
Then the map
![]() $P:L_1(X)\to L_1(X)$
given by
$P:L_1(X)\to L_1(X)$
given by
(recall that
![]() $\mu _I=\|\chi _I\|^{-1}_X$
and
$\mu _I=\|\chi _I\|^{-1}_X$
and
![]() $\nu _L=\|\chi _L\|_{X^*}^{-1}$
) is a norm-one projection onto
$\nu _L=\|\chi _L\|_{X^*}^{-1}$
) is a norm-one projection onto
![]() $Z(X) = \overline {\langle \widetilde h_I\otimes \widehat h_L: I,L\in \mathcal {D}^+ \rangle }$
, and the map
$Z(X) = \overline {\langle \widetilde h_I\otimes \widehat h_L: I,L\in \mathcal {D}^+ \rangle }$
, and the map
is a linear isometry onto
![]() $Z(X)$
. Then any bounded linear operator
$Z(X)$
. Then any bounded linear operator
![]() $T:L_1(X)\to L_1(X)$
is a 1-projectional factor of
$T:L_1(X)\to L_1(X)$
is a 1-projectional factor of
![]() $S = A^{-1}PTA:L_1(X)\to L_1(X)$
, so that for all
$S = A^{-1}PTA:L_1(X)\to L_1(X)$
, so that for all
![]() $I,J,L,M\in \mathcal {D}^+$
, we have
$I,J,L,M\in \mathcal {D}^+$
, we have
Proposition 2.18. Let
![]() $\mathscr {A}\subset [\mathcal {D}^+]$
be a subset that has positive measure. Denote by
$\mathscr {A}\subset [\mathcal {D}^+]$
be a subset that has positive measure. Denote by
![]() $\mathcal {A} = \cup _{k_0=0}^\infty \{I_{k_0}:(I_k)_{k=0}^\infty \in \mathscr {A}\}$
and
$\mathcal {A} = \cup _{k_0=0}^\infty \{I_{k_0}:(I_k)_{k=0}^\infty \in \mathscr {A}\}$
and
![]() $Y_{\mathscr {A}} = \overline {\langle \{h_I:I\in \mathcal {A}\}\rangle }$
. Then there exists a subspace Z of
$Y_{\mathscr {A}} = \overline {\langle \{h_I:I\in \mathcal {A}\}\rangle }$
. Then there exists a subspace Z of
![]() $Y_{\mathscr {A}}$
, which is isometrically isomorphic to
$Y_{\mathscr {A}}$
, which is isometrically isomorphic to
![]() $L_1$
and
$L_1$
and
![]() $1$
-complemented in
$1$
-complemented in
![]() $L_1$
.
$L_1$
.
Proof. By approximating
![]() $\mathscr {A}$
in measure by closed sets from the inside, we can assume that
$\mathscr {A}$
in measure by closed sets from the inside, we can assume that
![]() $\mathscr {A}$
is closed. For
$\mathscr {A}$
is closed. For
![]() $k\in \mathbb {N}$
, let
$k\in \mathbb {N}$
, let
![]() $A_k = \cup \{I:I\in \mathcal {A}\cap \mathcal {D}_k\}$
and
$A_k = \cup \{I:I\in \mathcal {A}\cap \mathcal {D}_k\}$
and
that is,
![]() $\mathscr {A}_k$
is the set of all sequences
$\mathscr {A}_k$
is the set of all sequences
![]() $(I_n)_{n=0}^\infty $
in
$(I_n)_{n=0}^\infty $
in
![]() $[\mathcal D^+]$
such that the k’th entry
$[\mathcal D^+]$
such that the k’th entry
![]() $I_k$
is a subset of
$I_k$
is a subset of
![]() $A_k$
. Then it follows that
$A_k$
. Then it follows that
![]() $\mathscr {A}=\bigcap _k \mathscr {A}_k$
, and letting
$\mathscr {A}=\bigcap _k \mathscr {A}_k$
, and letting
![]() $A = \cap _k A_k$
, we deduce that
$A = \cap _k A_k$
, we deduce that
But also, for any
![]() $J\notin \mathcal {A}$
, we have
$J\notin \mathcal {A}$
, we have
![]() $J\cap A=\emptyset $
. It follows that for any
$J\cap A=\emptyset $
. It follows that for any
![]() $f\in L_1$
with
$f\in L_1$
with
![]() $f|_{A^c} = 0$
and
$f|_{A^c} = 0$
and
![]() $J\notin \mathcal {A}$
, we have
$J\notin \mathcal {A}$
, we have
![]() $\langle h_J, f\rangle = 0$
and thus
$\langle h_J, f\rangle = 0$
and thus
![]() $f\in Y_{\mathscr {A}}$
. In particular, the restriction operator
$f\in Y_{\mathscr {A}}$
. In particular, the restriction operator
![]() $R_A:L_1\to L_1$
is a 1-projection onto a subspace that is isometrically isomorphic to
$R_A:L_1\to L_1$
is a 1-projection onto a subspace that is isometrically isomorphic to
![]() $L_1$
.
$L_1$
.
The above proposition leads to the following example, which will be useful in the sequel.
Example 2.19. Let
![]() $\mathscr {A}\subset [\mathcal {D}^+]$
be a subset that has positive measure, and let X be a Banach space. Then there exists a subspace Z of
$\mathscr {A}\subset [\mathcal {D}^+]$
be a subset that has positive measure, and let X be a Banach space. Then there exists a subspace Z of
![]() $Y_{\mathscr {A}}$
that is isometrically isomorphic to
$Y_{\mathscr {A}}$
that is isometrically isomorphic to
![]() $L_1$
via
$L_1$
via
![]() $A:L_1\to Z$
and 1-complemented in
$A:L_1\to Z$
and 1-complemented in
![]() $L_1$
via
$L_1$
via
![]() $P:L_1\to Z$
. In particular, for any Banach space X, the space
$P:L_1\to Z$
. In particular, for any Banach space X, the space
is isometrically isomorphic to
![]() $L_1(X)$
via
$L_1(X)$
via
![]() $A\otimes I:L_1(X)\to Z(X)$
and 1-complemented in
$A\otimes I:L_1(X)\to Z(X)$
and 1-complemented in
![]() $L_1(X)$
via
$L_1(X)$
via
![]() $P\otimes I$
.
$P\otimes I$
.
2.6 Decompositions of operators on
 $L_1(X)$
$L_1(X)$
We begin by listing further standard facts about projective tensor products. We then use these facts to associate to each bounded linear operator
![]() $T\!:\!L_1(X)\to L_1(X)$
a family of bounded linear operators on
$T\!:\!L_1(X)\to L_1(X)$
a family of bounded linear operators on
![]() $L_1$
. In the next section, we will study the compactness properties of this family. In later sections, we use these properties to extract information about projectional factors of the operator T.
$L_1$
. In the next section, we will study the compactness properties of this family. In later sections, we use these properties to extract information about projectional factors of the operator T.
Let E, F be Banach spaces.
-
(a) For every
 $e_0^*\in E^*$
and
$e_0^*\in E^*$
and
 $f_0^*\in F^*$
, we may define the bounded linear maps
$f_0^*\in F^*$
, we may define the bounded linear maps
 $q_{(e_0^*)}:E\otimes _\pi F\to F$
and
$q_{(e_0^*)}:E\otimes _\pi F\to F$
and
 $q^{(f_0^*)}:E\otimes _\pi F\to E$
given by
$q^{(f_0^*)}:E\otimes _\pi F\to E$
given by
 $q_{(e_0^*)}(e\otimes f) = e_0^*(e)f$
and
$q_{(e_0^*)}(e\otimes f) = e_0^*(e)f$
and
 $q^{(f_0^*)}(e\otimes f) = f_0^*(f)e$
. Then
$q^{(f_0^*)}(e\otimes f) = f_0^*(f)e$
. Then
 $\|q_{(e_0^*)}\| = \|e_0^*\|$
and
$\|q_{(e_0^*)}\| = \|e_0^*\|$
and
 $\|q^{(f_0^*)}\| = \|f_0^*\|$
.
$\|q^{(f_0^*)}\| = \|f_0^*\|$
. -
(b) For every
 $e_0\in E$
and
$e_0\in E$
and
 $f_0\in F$
, we may define the maps
$f_0\in F$
, we may define the maps
 $j_{(e_0)}:F\to E\otimes _\pi F$
and
$j_{(e_0)}:F\to E\otimes _\pi F$
and
 $j^{(f_0)}:E\to E\otimes _\pi F$
given by
$j^{(f_0)}:E\to E\otimes _\pi F$
given by
 $j_{(e_0)}f = e_0\otimes f$
and
$j_{(e_0)}f = e_0\otimes f$
and
 $j^{(f_0)}e = e\otimes f_0$
. Then
$j^{(f_0)}e = e\otimes f_0$
. Then
 $\|j_{(e_0)}\| = \|e_0\|$
and
$\|j_{(e_0)}\| = \|e_0\|$
and
 $\|j^{(f_0)}\| = \|f_0\|$
.
$\|j^{(f_0)}\| = \|f_0\|$
. -
(c) For every bounded linear operator
 $T:E\otimes _\pi F\to E\otimes _\pi F$
,
$T:E\otimes _\pi F\to E\otimes _\pi F$
,
 $f_0^*\in F^*$
, and
$f_0^*\in F^*$
, and
 $f_0\in F$
, the map
$f_0\in F$
, the map
 $T^{(f_0^*,f_0)}:=q^{(f_0^*)}Tj^{(f_0)}:E\to E$
is the unique bounded linear map so that for all
$T^{(f_0^*,f_0)}:=q^{(f_0^*)}Tj^{(f_0)}:E\to E$
is the unique bounded linear map so that for all
 $e^*\in E^*$
and
$e^*\in E^*$
and
 $e\in E$
, we have
$e\in E$
, we have
 $\langle e^*, T^{(f_0^*,f_0)}e\rangle = \langle e^*\otimes f_0^*, T(e\otimes f_0)\rangle $
.
$\langle e^*, T^{(f_0^*,f_0)}e\rangle = \langle e^*\otimes f_0^*, T(e\otimes f_0)\rangle $
. -
(d) For every bounded linear operator
 $T:E\otimes _\pi F\to E\otimes _\pi F$
,
$T:E\otimes _\pi F\to E\otimes _\pi F$
,
 $e_0^*\in E^*$
and
$e_0^*\in E^*$
and
 $e_0\in E$
, the map
$e_0\in E$
, the map
 $T_{(e_0^*,e_0)}:=q_{(e_0^*)}Tj_{(e_0)}:F\to F$
is the unique bounded linear map so that for all
$T_{(e_0^*,e_0)}:=q_{(e_0^*)}Tj_{(e_0)}:F\to F$
is the unique bounded linear map so that for all
 $f^*\in F^*$
and
$f^*\in F^*$
and
 $f\in F$
, we have
$f\in F$
, we have
 $\langle f^*, T_{(e_0^*,e_0)}f\rangle = \langle e_0^*\otimes f^*, T(e_0\otimes f)\rangle $
.
$\langle f^*, T_{(e_0^*,e_0)}f\rangle = \langle e_0^*\otimes f^*, T(e_0\otimes f)\rangle $
.
Notation. Let X be a Haar system space. For
![]() $L\in \mathcal {D}^+$
, we denote
$L\in \mathcal {D}^+$
, we denote
-
(i)
 $q^L = q^{(\nu _Lh_L)}:L_1(X)\to L_1$
,
$q^L = q^{(\nu _Lh_L)}:L_1(X)\to L_1$
, -
(ii)
 $j^L = j^{(\mu _Lh_L)}:L_1\to L_1(X)$
, and
$j^L = j^{(\mu _Lh_L)}:L_1\to L_1(X)$
, and -
(iii)
 $P^L = j^Lq^L:L_1(X)\to L_1(X)$
.
$P^L = j^Lq^L:L_1(X)\to L_1(X)$
.
Note that for any
![]() $k\in \mathbb {N}$
,
$k\in \mathbb {N}$
,
![]() $\|\sum _{\{L:\iota (L)\leq k\}}P^L\| = 1$
. This is because this operator coincides with
$\|\sum _{\{L:\iota (L)\leq k\}}P^L\| = 1$
. This is because this operator coincides with
![]() $I\otimes P^{[\iota \leq k]}$
, where
$I\otimes P^{[\iota \leq k]}$
, where
![]() $P^{[\iota \leq k]}:X\to X$
is the basis projection onto
$P^{[\iota \leq k]}:X\to X$
is the basis projection onto
![]() $(\mu _Lh_L)_{\iota (L)\leq k}$
(this is easy to verify on vectors of the form
$(\mu _Lh_L)_{\iota (L)\leq k}$
(this is easy to verify on vectors of the form
![]() $u =h_I\otimes h_L$
whose linear span is dense in
$u =h_I\otimes h_L$
whose linear span is dense in
![]() $L_1(X)$
). We may therefore state the following.
$L_1(X)$
). We may therefore state the following.
Remark 2.20. Let X be a Haar system space.
-
(i) For each
 $L\in \mathcal {D}^+$
,
$L\in \mathcal {D}^+$
,
 $P^L$
is a projection with image that is isometrically isomorphic to
$P^L$
is a projection with image that is isometrically isomorphic to $$\begin{align*}Y^L = \{f\otimes (\mu_Lh_L): f\in L_1\}\end{align*}$$
$$\begin{align*}Y^L = \{f\otimes (\mu_Lh_L): f\in L_1\}\end{align*}$$
 $L_1$
.
$L_1$
.
-
(ii)
 $(Y^L)_{L\in \mathcal {D}^+}$
forms a monotone Schauder decomposition of
$(Y^L)_{L\in \mathcal {D}^+}$
forms a monotone Schauder decomposition of
 $L_1(X)$
. In particular, for every
$L_1(X)$
. In particular, for every
 $u\in L_1(X)$
, Thus, u admits a unique representation
$u\in L_1(X)$
, Thus, u admits a unique representation $$\begin{align*}u = \sum_{L\in\mathcal{D}^+} P^Lu =\sum_{L\in\mathcal{D}^+} (q^Lu)\otimes (\mu_Lh_L).\end{align*}$$
$$\begin{align*}u = \sum_{L\in\mathcal{D}^+} P^Lu =\sum_{L\in\mathcal{D}^+} (q^Lu)\otimes (\mu_Lh_L).\end{align*}$$
 $u = \sum _{L\in \mathcal {D}^+}f_L\otimes (\mu _Lh_L)$
.
$u = \sum _{L\in \mathcal {D}^+}f_L\otimes (\mu _Lh_L)$
.
2.7 Operators on
 $L_1$
associated to an operator on
$L_1$
associated to an operator on
 $L_1(X)$
$L_1(X)$
For a Haar system space X, we represent every bounded linear operator
![]() $T:L_1(X)\to L_1(X)$
as a matrix of operators
$T:L_1(X)\to L_1(X)$
as a matrix of operators
![]() $(T^{(L,M)})_{(L,M)\in \mathcal {D}^+}$
, each of which is defined on
$(T^{(L,M)})_{(L,M)\in \mathcal {D}^+}$
, each of which is defined on
![]() $L_1$
.
$L_1$
.
Notation. Let X be a Haar system space, and let
![]() $T:L_1(X)\to L_1(X)$
be a bounded linear operator. For
$T:L_1(X)\to L_1(X)$
be a bounded linear operator. For
![]() $L,M\in \mathcal {D}^+$
, we denote
$L,M\in \mathcal {D}^+$
, we denote
![]() $T^{(L,M)} = T^{(\nu _Lh_L,\mu _Mh_M)}$
(recall from Proposition 2.13 that the scalars
$T^{(L,M)} = T^{(\nu _Lh_L,\mu _Mh_M)}$
(recall from Proposition 2.13 that the scalars
![]() $\mu _M$
and
$\mu _M$
and
![]() $\nu _L$
are positive and chosen so that
$\nu _L$
are positive and chosen so that
![]() $\mu _Mh_M$
is normalised in
$\mu _Mh_M$
is normalised in
![]() $X^*$
and
$X^*$
and
![]() $\nu _L h_L$
is normalised in X), so that for every
$\nu _L h_L$
is normalised in X), so that for every
![]() $u\in L_1(X)$
, we have
$u\in L_1(X)$
, we have
 $$ \begin{align} Tu &= \sum_{L\in\mathcal{D}^+}P^LT\Big(\sum_{M\in\mathcal{D}^+}P^Mu\Big) = \sum_{L\in\mathcal{D}^+}\sum_{M\in\mathcal{D}^+}j^LT^{(L,M)}q^Mu\nonumber\\ &= \sum_{L\in\mathcal{D}^+}\sum_{M\in\mathcal{D}^+}\Big(T^{(L,M)}(q^Mu)\Big)\otimes(\mu_Lh_L). \end{align} $$
$$ \begin{align} Tu &= \sum_{L\in\mathcal{D}^+}P^LT\Big(\sum_{M\in\mathcal{D}^+}P^Mu\Big) = \sum_{L\in\mathcal{D}^+}\sum_{M\in\mathcal{D}^+}j^LT^{(L,M)}q^Mu\nonumber\\ &= \sum_{L\in\mathcal{D}^+}\sum_{M\in\mathcal{D}^+}\Big(T^{(L,M)}(q^Mu)\Big)\otimes(\mu_Lh_L). \end{align} $$
For
![]() $L\in \mathcal {D}^+$
, we denote
$L\in \mathcal {D}^+$
, we denote
![]() $T^L = T^{(L,L)}$
.
$T^L = T^{(L,L)}$
.
The following type of operator is essential as it is easier to work with. A significant part of the paper shows that within the constraints of the problem under consideration, every operator
![]() $T:L_1(X)\to L_1(X)$
is a 1-projectional factor with error
$T:L_1(X)\to L_1(X)$
is a 1-projectional factor with error
![]() $\varepsilon $
of an X-diagonal operator.
$\varepsilon $
of an X-diagonal operator.
Definition 2.21. Let X be a Haar system space. A bounded linear operator
![]() $T:L_1(X)\to L_1(X)$
is called X-diagonal if for all
$T:L_1(X)\to L_1(X)$
is called X-diagonal if for all
![]() $L\neq M\in \mathcal {D}^+$
,
$L\neq M\in \mathcal {D}^+$
,
![]() $T^{(L,M)} = 0$
. We then call
$T^{(L,M)} = 0$
. We then call
![]() $(T^L)_{L\in \mathcal {D}^+}$
the entries of T.
$(T^L)_{L\in \mathcal {D}^+}$
the entries of T.
Note that T is X-diagonal if and only if for all
![]() $f\in L_1$
and
$f\in L_1$
and
![]() $L\in \mathcal {D}^+$
, we have
$L\in \mathcal {D}^+$
, we have
![]() $T(f\otimes (\mu _Lh_L)) = (T^Lf)\otimes (\mu _Lh_L)$
if and only if for all
$T(f\otimes (\mu _Lh_L)) = (T^Lf)\otimes (\mu _Lh_L)$
if and only if for all
![]() $L\in \mathcal {D}^+$
, the space
$L\in \mathcal {D}^+$
, the space
![]() $Y^L$
is T-invariant.
$Y^L$
is T-invariant.
Remark 2.22. If X is a Haar system space and
![]() $T:L_1(X)\to L_1(X)$
is a bounded linear operator so that
$T:L_1(X)\to L_1(X)$
is a bounded linear operator so that
![]() $\sum _{L\neq M}\|T^{(L,M)}\| = \varepsilon <\infty $
, then equation (29) yields that there exists an X-diagonal operator
$\sum _{L\neq M}\|T^{(L,M)}\| = \varepsilon <\infty $
, then equation (29) yields that there exists an X-diagonal operator
![]() $\bar {T}:L_1(X)\to L_1(X)$
with entries
$\bar {T}:L_1(X)\to L_1(X)$
with entries
![]() $(T^L)_{L\in \mathcal {D}^+}$
so that
$(T^L)_{L\in \mathcal {D}^+}$
so that
![]() $\|T - \bar {T}\| \leq \varepsilon $
.
$\|T - \bar {T}\| \leq \varepsilon $
.
3 Compactness properties of families of operators
In this section, we extract compactness properties of families of operators associated to a
![]() $T:L_1(X)\to L_1(X)$
. These results will eventually be applied to families that resemble ones of the form
$T:L_1(X)\to L_1(X)$
. These results will eventually be applied to families that resemble ones of the form
![]() $(T^{(L,M)})_{(L,M)\in \mathcal {D}^+}$
. The achieved compactness will be used later in a regularisation process that will allow us to extract ‘nicer’ operators that projectionally factor through T. We have chosen to present this section in a more abstract setting that permits more elegant statements and proofs.
$(T^{(L,M)})_{(L,M)\in \mathcal {D}^+}$
. The achieved compactness will be used later in a regularisation process that will allow us to extract ‘nicer’ operators that projectionally factor through T. We have chosen to present this section in a more abstract setting that permits more elegant statements and proofs.
3.1 WOT-sequentially compact families
Taking WOT-limits of certain sequences of operators of the form
![]() $T^{(x^*,x)}$
is an important component of the proof. This element was already present in the approach of Capon [Reference Capon11, Reference Capon12].
$T^{(x^*,x)}$
is an important component of the proof. This element was already present in the approach of Capon [Reference Capon11, Reference Capon12].
This essential Lemma due to Rosenthal is necessary in this subsection as well as the next one. A proof can be given, for example, by induction on j for
![]() $\varepsilon = 2^{-j}\sup _n\|\xi _n\|_1$
.
$\varepsilon = 2^{-j}\sup _n\|\xi _n\|_1$
.
Lemma 3.1 [Reference Rosenthal32, Lemma 1.1]
Let
![]() $(\xi _n)_n$
be a bounded sequence of elements of
$(\xi _n)_n$
be a bounded sequence of elements of
![]() $\ell _1$
and
$\ell _1$
and
![]() $\varepsilon>0$
. Then there exists an infinite set
$\varepsilon>0$
. Then there exists an infinite set
![]() $N = \{n_j:j\in \mathbb {N}\}\in [\mathbb {N}]^\infty $
so that for every
$N = \{n_j:j\in \mathbb {N}\}\in [\mathbb {N}]^\infty $
so that for every
![]() $j_0\in \mathbb {N}$
, we have
$j_0\in \mathbb {N}$
, we have
![]() $\sum _{j\neq j_0}|\xi _{n_{j_0}}(n_j)| \leq \varepsilon $
.
$\sum _{j\neq j_0}|\xi _{n_{j_0}}(n_j)| \leq \varepsilon $
.
Here, WOT stands for the weak operator topology in
![]() $L_1(X)$
.
$L_1(X)$
.
Theorem 3.2. Let X be a Banach space,
![]() $T:L_1(X)\to L_1(X)$
be a bounded linear operator and A, B be bounded subsets of
$T:L_1(X)\to L_1(X)$
be a bounded linear operator and A, B be bounded subsets of
![]() $X^*$
and X, respectively. Assume that B contains no sequence that is equivalent to the unit vector basis of
$X^*$
and X, respectively. Assume that B contains no sequence that is equivalent to the unit vector basis of
![]() $\ell _1$
. Then for every
$\ell _1$
. Then for every
![]() $f\in L_1$
, the set
$f\in L_1$
, the set
is a uniformly integrable (and thus weakly relatively compact) subset of
![]() $L_1$
. In particular, every sequence in
$L_1$
. In particular, every sequence in
![]() $\{T^{(x^*,x)}: (x^*,x)\in A\times B\}$
has a WOT-convergent subsequence.
$\{T^{(x^*,x)}: (x^*,x)\in A\times B\}$
has a WOT-convergent subsequence.
Proof. The ‘in particular’ part follows from the separability of
![]() $L_1$
and the fact that the set in question if bounded by
$L_1$
and the fact that the set in question if bounded by
![]() $\|T\|\sup _{(x^*,x)\in A\times B}\|x^*\|\|x\|$
.
$\|T\|\sup _{(x^*,x)\in A\times B}\|x^*\|\|x\|$
.
Fix a sequence
![]() $(x_n^*,x_n)\in A\times B$
. Assume that
$(x_n^*,x_n)\in A\times B$
. Assume that
![]() $(T^{(x_n^*,x_n)}f)_n$
is not uniformly integrable. Then after passing to a subsequence, there exist
$(T^{(x_n^*,x_n)}f)_n$
is not uniformly integrable. Then after passing to a subsequence, there exist
![]() $\delta>0$
and a sequence of disjoint measurable subsets
$\delta>0$
and a sequence of disjoint measurable subsets
![]() $(A_n)_n$
of
$(A_n)_n$
of
![]() $[0,1)$
so that for all
$[0,1)$
so that for all
![]() $n\in \mathbb {N}$
, we have
$n\in \mathbb {N}$
, we have
For every
![]() $n\in \mathbb {N}$
, define the scalar sequence
$n\in \mathbb {N}$
, define the scalar sequence
![]() $\xi _n = (\xi _n(m))_m$
given by
$\xi _n = (\xi _n(m))_m$
given by
![]() $\xi _n(m) = \langle \chi _{A_m}\otimes x_m^*,T(f\otimes x_n)\rangle $
. Then for every
$\xi _n(m) = \langle \chi _{A_m}\otimes x_m^*,T(f\otimes x_n)\rangle $
. Then for every
![]() $m_0\in \mathbb {N}$
, we have that for appropriate scalars
$m_0\in \mathbb {N}$
, we have that for appropriate scalars
![]() $(\zeta _m)_{m=1}^N$
of modulus one,
$(\zeta _m)_{m=1}^N$
of modulus one,
 $$ \begin{align} \sum_{m=1}^{m_0}|\xi_n(m)| &= \Big|\big\langle\sum_{m=1}^{m_0}\chi_{A_m}\otimes \zeta_mx_m^*,T(f\otimes x_n)\big\rangle\Big|\\\nonumber & \leq \underbrace{\Big\|\sum_{m=1}^{m_0}\chi_{A_{m}}\otimes (\zeta_m x^*_{m})\Big\|}_{= \max_{1\leq m\leq m_0}\|x^*_{m}\|}\|T\|\|f\| \|x_n\|\nonumber\\ &\leq \|T\|\|f\|\sup_{(x^*,x)\in A\times B}\|x^*\|\|x\|.\nonumber \end{align} $$
$$ \begin{align} \sum_{m=1}^{m_0}|\xi_n(m)| &= \Big|\big\langle\sum_{m=1}^{m_0}\chi_{A_m}\otimes \zeta_mx_m^*,T(f\otimes x_n)\big\rangle\Big|\\\nonumber & \leq \underbrace{\Big\|\sum_{m=1}^{m_0}\chi_{A_{m}}\otimes (\zeta_m x^*_{m})\Big\|}_{= \max_{1\leq m\leq m_0}\|x^*_{m}\|}\|T\|\|f\| \|x_n\|\nonumber\\ &\leq \|T\|\|f\|\sup_{(x^*,x)\in A\times B}\|x^*\|\|x\|.\nonumber \end{align} $$
By Rosenthal’s Lemma 3.1, there exists an infinite subset
![]() $N = \{n_j:j\in \mathbb {N}\}$
of
$N = \{n_j:j\in \mathbb {N}\}$
of
![]() $\mathbb {N}$
so that for all
$\mathbb {N}$
so that for all
![]() $i_0\in \mathbb {N}$
, we have
$i_0\in \mathbb {N}$
, we have
![]() $\sum _{j\neq i_0}|\xi _{n_{i_0}}(n_j)| \leq \delta /2$
. After relabelling, for all
$\sum _{j\neq i_0}|\xi _{n_{i_0}}(n_j)| \leq \delta /2$
. After relabelling, for all
![]() $n_0\in \mathbb {N}$
, we have
$n_0\in \mathbb {N}$
, we have
We now show that
![]() $(x_n)_n$
is equivalent to the unit vector basis of
$(x_n)_n$
is equivalent to the unit vector basis of
![]() $\ell _1$
. Fix scalars
$\ell _1$
. Fix scalars
![]() $a_1,\ldots ,a_N$
. For appropriate scalars
$a_1,\ldots ,a_N$
. For appropriate scalars
![]() $\theta _1,\ldots ,\theta _N$
of modulus 1, we have
$\theta _1,\ldots ,\theta _N$
of modulus 1, we have
 $$ \begin{align} \sum_{n=1}^Na_n\theta_n\langle \chi_{A_{n}}\otimes x^*_{n},T(f\otimes x_{n})\rangle \geq \delta\sum_{n=1}^N|a_n|. \end{align} $$
$$ \begin{align} \sum_{n=1}^Na_n\theta_n\langle \chi_{A_{n}}\otimes x^*_{n},T(f\otimes x_{n})\rangle \geq \delta\sum_{n=1}^N|a_n|. \end{align} $$
Put
 $$ \begin{align*} \Lambda & = \Big|\big\langle\sum_{m=1}^N\chi_{A_{m}}\otimes (\theta_m x^*_{m}),T\big(\sum_{n=1}^Nf\otimes a_nx_{n}\big)\big\rangle\Big|\\ &\leq \underbrace{\Big\|\sum_{m=1}^N\chi_{A_{m}}\otimes (\theta_m x^*_{m})\Big\|}_{= \max_{1\leq m\leq N}\|x^*_{m}\|}\|T\|\|f\| \Big\|\sum_{n=1}^Na_nx_n\Big\|\\ &\leq \|T\|\|f\|\sup_{x^*\in A}\|x^*\|\Big\|\sum_{n=1}^Na_nx_n\Big\|. \end{align*} $$
$$ \begin{align*} \Lambda & = \Big|\big\langle\sum_{m=1}^N\chi_{A_{m}}\otimes (\theta_m x^*_{m}),T\big(\sum_{n=1}^Nf\otimes a_nx_{n}\big)\big\rangle\Big|\\ &\leq \underbrace{\Big\|\sum_{m=1}^N\chi_{A_{m}}\otimes (\theta_m x^*_{m})\Big\|}_{= \max_{1\leq m\leq N}\|x^*_{m}\|}\|T\|\|f\| \Big\|\sum_{n=1}^Na_nx_n\Big\|\\ &\leq \|T\|\|f\|\sup_{x^*\in A}\|x^*\|\Big\|\sum_{n=1}^Na_nx_n\Big\|. \end{align*} $$
Also,
 $$ \begin{align*} \Lambda & = \Big|\sum_{n=1}^Na_n\theta_n\langle \chi_{A_{n}}\otimes x^*_{n},T(f\otimes x_{n})\rangle + \sum_{n=1}^Na_n\sum_{m\neq n}\theta_m\langle \chi_{A_{m}}\otimes x^*_{m},T(f\otimes x_{n})\rangle\Big|\\ &\geq \delta\sum_{n=1}^N|a_n| - \sum_{n=1}^N|a_n|\sum_{m\neq n}|\xi_n(m)| \geq \delta/2\sum_{n=1}^N|a_n|. \end{align*} $$
$$ \begin{align*} \Lambda & = \Big|\sum_{n=1}^Na_n\theta_n\langle \chi_{A_{n}}\otimes x^*_{n},T(f\otimes x_{n})\rangle + \sum_{n=1}^Na_n\sum_{m\neq n}\theta_m\langle \chi_{A_{m}}\otimes x^*_{m},T(f\otimes x_{n})\rangle\Big|\\ &\geq \delta\sum_{n=1}^N|a_n| - \sum_{n=1}^N|a_n|\sum_{m\neq n}|\xi_n(m)| \geq \delta/2\sum_{n=1}^N|a_n|. \end{align*} $$
Thus,
![]() $\|\sum _{n=1}^Na_nx_n\| \geq c\sum _{n=1}^N|a_n|$
, where
$\|\sum _{n=1}^Na_nx_n\| \geq c\sum _{n=1}^N|a_n|$
, where
![]() $c = \delta /(2\|T\|\|f\|\sup _{x^*\in A}\|x^*\|)$
.
$c = \delta /(2\|T\|\|f\|\sup _{x^*\in A}\|x^*\|)$
.
3.2 Compactness in operator norm
We discuss families that are uniformly eventually close to multipliers and how to obtain compact sets from them. This is particularly important in the sequel because compactness will be essential in achieving strong stabilisation properties of operators
![]() $T:L_1(X)\to L_1(X)$
.
$T:L_1(X)\to L_1(X)$
.
Notation. For
![]() $n\in \mathbb {N}$
, we denote by
$n\in \mathbb {N}$
, we denote by
![]() $P_{(\leq n)}:L_1\to L_1$
the norm-one canonical basis projection onto
$P_{(\leq n)}:L_1\to L_1$
the norm-one canonical basis projection onto
![]() $\langle \{h_I:I\in \mathcal {D}^n\}\rangle $
. We also denote
$\langle \{h_I:I\in \mathcal {D}^n\}\rangle $
. We also denote
![]() $P_{(>n)} = I - P_{(\leq n)}$
.
$P_{(>n)} = I - P_{(\leq n)}$
.
Definition 3.3. A set
![]() $\mathscr {T}$
of bounded linear operators on
$\mathscr {T}$
of bounded linear operators on
![]() $L_1$
is called uniformly eventually close to Haar multipliers if there exists a collection
$L_1$
is called uniformly eventually close to Haar multipliers if there exists a collection
![]() $(D_T)_{T\in \mathscr {T}}$
in
$(D_T)_{T\in \mathscr {T}}$
in
![]() $\mathcal {L}_{HM}(L_1)$
so that
$\mathcal {L}_{HM}(L_1)$
so that
The main result of this subsection is the first one in the paper that requires a certain amount of legwork.
Theorem 3.4 Fundamental Lemma
Let X be a Banach space, A, B be bounded subsets of
![]() $X^*$
and X, respectively, and
$X^*$
and X, respectively, and
![]() $C\subset A\times B$
. Let
$C\subset A\times B$
. Let
![]() $T:L_1(X)\to L_1(X)$
be a bounded linear operator, and assume the following:
$T:L_1(X)\to L_1(X)$
be a bounded linear operator, and assume the following:
-
(i) The set B contains no sequence that is equivalent to the unit vector basis of
 $\ell _1$
.
$\ell _1$
. -
(ii) The set
 $\{T^{(x^*,x)}:(x^*,x)\in C\}$
is uniformly eventually close to Haar multipliers.
$\{T^{(x^*,x)}:(x^*,x)\in C\}$
is uniformly eventually close to Haar multipliers.
Then for every
![]() $\eta>0$
, there exists a closed subset
$\eta>0$
, there exists a closed subset
![]() $\mathscr {A}$
of
$\mathscr {A}$
of
![]() $[\mathcal {D}^+]$
with
$[\mathcal {D}^+]$
with
![]() $|\mathscr {A}|>1-\eta $
so that the set
$|\mathscr {A}|>1-\eta $
so that the set
![]() $\{T^{(x^*,x)}P_{\mathscr {A}}:(x^*,x)\in C\}$
is relatively compact in the operator norm topology.
$\{T^{(x^*,x)}P_{\mathscr {A}}:(x^*,x)\in C\}$
is relatively compact in the operator norm topology.
Remark 3.5. It is not hard to see that the unit ball of
![]() $\mathcal {L}_{HM}(L_1)$
is a compact set in the strong operator topology of
$\mathcal {L}_{HM}(L_1)$
is a compact set in the strong operator topology of
![]() $L_1$
. In fact, this is the
$L_1$
. In fact, this is the
![]() $w^*$
-topology inherited by a predual of
$w^*$
-topology inherited by a predual of
![]() $\mathcal {L}_{HM}(L_1)$
, namely Rosenthal’s Stopping Time space studied by Bang and Odell in [Reference Bang and Odell4, Reference Bang and Odell5], by Dew in [Reference Dew14] and by Apatsidis in [Reference Apatsidis2]. The Fundamental Lemma (Theorem 3.4) states that under the right conditions, strong operator convergence yields convergence in operator norm on a big subspace of
$\mathcal {L}_{HM}(L_1)$
, namely Rosenthal’s Stopping Time space studied by Bang and Odell in [Reference Bang and Odell4, Reference Bang and Odell5], by Dew in [Reference Dew14] and by Apatsidis in [Reference Apatsidis2]. The Fundamental Lemma (Theorem 3.4) states that under the right conditions, strong operator convergence yields convergence in operator norm on a big subspace of
![]() $L_1$
. Therefore, this is a type of Egorov Theorem. We point out that some restriction on the family of operators is necessary for the conclusion to hold. If one takes, for example,
$L_1$
. Therefore, this is a type of Egorov Theorem. We point out that some restriction on the family of operators is necessary for the conclusion to hold. If one takes, for example,
![]() $D_n = P_{(\leq n)}$
, then this converges to I in the strong operator topology. But for no nonempty set of branches
$D_n = P_{(\leq n)}$
, then this converges to I in the strong operator topology. But for no nonempty set of branches
![]() $\mathscr {A}$
, the set
$\mathscr {A}$
, the set
![]() $\{D_nP_{\mathscr {A}}:n\in \mathbb {N}\}$
is relatively compact in the operator norm topology.
$\{D_nP_{\mathscr {A}}:n\in \mathbb {N}\}$
is relatively compact in the operator norm topology.
Lemma 3.6. Let
![]() $r>0$
,
$r>0$
,
![]() $(I_k)_{k=0}^\infty \in [\mathcal {D}^+]$
associated to
$(I_k)_{k=0}^\infty \in [\mathcal {D}^+]$
associated to
![]() $(\theta _k)_{k=1}^\infty \in \{-1,1\}^{\mathbb {N}}$
and
$(\theta _k)_{k=1}^\infty \in \{-1,1\}^{\mathbb {N}}$
and
![]() $(a_k^n)_{(k,n)\in (\{0\}\cup \mathbb {N})\times \mathbb {N}}$
be a collection of scalars. Assume that there exist
$(a_k^n)_{(k,n)\in (\{0\}\cup \mathbb {N})\times \mathbb {N}}$
be a collection of scalars. Assume that there exist
![]() $k_1<\ell _1<k_2<\ell _2<\cdots $
so that for each
$k_1<\ell _1<k_2<\ell _2<\cdots $
so that for each
![]() $n\in \mathbb {N}$
, we have
$n\in \mathbb {N}$
, we have
 $$\begin{align*}\sum_{k = k_n+1}^{\ell_n}|a^n_{k} - a^n_{k-1}| \geq r. \end{align*}$$
$$\begin{align*}\sum_{k = k_n+1}^{\ell_n}|a^n_{k} - a^n_{k-1}| \geq r. \end{align*}$$
For every
![]() $\ell ,n\in \mathbb {N}$
, define
$\ell ,n\in \mathbb {N}$
, define
![]() $f_n^\ell = \sum _{k=0}^\ell a_k^n\theta _k|I_k|^{-1}h_{I_k}$
. Then there exists a strictly increasing sequence of disjoint measurable subsets
$f_n^\ell = \sum _{k=0}^\ell a_k^n\theta _k|I_k|^{-1}h_{I_k}$
. Then there exists a strictly increasing sequence of disjoint measurable subsets
![]() $(A_n)_n$
of
$(A_n)_n$
of
![]() $[0,1)$
so that for all
$[0,1)$
so that for all
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $\ell \geq \ell _n$
, we have
$\ell \geq \ell _n$
, we have
Proof. Let
![]() $(B_k)$
be the partition of
$(B_k)$
be the partition of
![]() $[0,1)$
defined by
$[0,1)$
defined by
![]() $B_k=I_k\setminus I_{k+1}$
,
$B_k=I_k\setminus I_{k+1}$
,
![]() $k\in \mathbb {N}$
. We conclude from the inequality in equation (22) in Proposition 2.5 that:
$k\in \mathbb {N}$
. We conclude from the inequality in equation (22) in Proposition 2.5 that:
-
(i) for every
 $k \leq \ell _n \leq \ell \in \mathbb {N}$
and
$k \leq \ell _n \leq \ell \in \mathbb {N}$
and
 $s\in B_k$
, we have
$s\in B_k$
, we have
 $f_n^\ell (s) = f^{\ell _n}_n(s)$
and
$f_n^\ell (s) = f^{\ell _n}_n(s)$
and -
(ii) for every
 $m\leq \ell _n\in \mathbb {N}$
, we have
$m\leq \ell _n\in \mathbb {N}$
, we have  $$\begin{align*}\int_{\cup_{k=m}^{\ell_n} B_k}|f_n^{\ell_n}(s)|ds \geq \frac{1}{3}\sum_{k=m+1}^{\ell_n} |a_k - a_{k-1}|.\end{align*}$$
$$\begin{align*}\int_{\cup_{k=m}^{\ell_n} B_k}|f_n^{\ell_n}(s)|ds \geq \frac{1}{3}\sum_{k=m+1}^{\ell_n} |a_k - a_{k-1}|.\end{align*}$$
Put
![]() $A_n = \cup _{i=k_n}^{\ell _n}B_i$
. The conclusion follows directly from (i) and (ii).
$A_n = \cup _{i=k_n}^{\ell _n}B_i$
. The conclusion follows directly from (i) and (ii).
Proof of Theorem 3.4
Put
![]() $\mathscr {T} = \{T^{(x^*,x)}:(x^*,x)\in A\times B\}$
. Take a family
$\mathscr {T} = \{T^{(x^*,x)}:(x^*,x)\in A\times B\}$
. Take a family
![]() $(D_T)_{T}$
as in Definition 3.3. For each
$(D_T)_{T}$
as in Definition 3.3. For each
![]() $T\in \mathscr {T}$
, we have
$T\in \mathscr {T}$
, we have
 $$ \begin{align} \|P_{(>k)}TP_{(\leq k)}\| &\leq \underbrace{\big\|P_{(>k)}D_TP_{(\leq k)}\big\|}_{=0} + \big\|P_{(>k)}(T - D_T)P_{(\leq k)}\big\|\nonumber\\ &\leq \big\|P_{(>k)}(T - D_T)\|\nonumber\\ &\leq \sup_{S\in\mathscr{T}}\Big(\big\|P_{(>k)}(S- D_S)\big\|\Big) \!=\!\delta_k. \end{align} $$
$$ \begin{align} \|P_{(>k)}TP_{(\leq k)}\| &\leq \underbrace{\big\|P_{(>k)}D_TP_{(\leq k)}\big\|}_{=0} + \big\|P_{(>k)}(T - D_T)P_{(\leq k)}\big\|\nonumber\\ &\leq \big\|P_{(>k)}(T - D_T)\|\nonumber\\ &\leq \sup_{S\in\mathscr{T}}\Big(\big\|P_{(>k)}(S- D_S)\big\|\Big) \!=\!\delta_k. \end{align} $$
Both
![]() $(\varepsilon _k)_k$
and
$(\varepsilon _k)_k$
and
![]() $(\delta _k)_k$
tend to zero. For each
$(\delta _k)_k$
tend to zero. For each
![]() $T\in \mathscr {T}$
, denote by
$T\in \mathscr {T}$
, denote by
![]() $(a^T_I)_{I\in \mathcal {D}^+}$
the entries of
$(a^T_I)_{I\in \mathcal {D}^+}$
the entries of
![]() $D_T$
.
$D_T$
.
Claim: Fix
![]() $\sigma = (I_k)_{k=1}^\infty \in [\mathcal {D}^+]$
and
$\sigma = (I_k)_{k=1}^\infty \in [\mathcal {D}^+]$
and
![]() $r>0$
. Then there exists
$r>0$
. Then there exists
![]() $k_0\in \mathbb {N}$
so that for all
$k_0\in \mathbb {N}$
so that for all
![]() $T\in \mathscr {T}$
, we have
$T\in \mathscr {T}$
, we have
![]() $\sum _{k=k_0}^\infty |a^T_{I_k} - a^T_{I_{k-1}}| \leq r$
.
$\sum _{k=k_0}^\infty |a^T_{I_k} - a^T_{I_{k-1}}| \leq r$
.
We will assume that the claim is true and proceed with the rest of the proof. For every
![]() $N,k_0,\in \mathbb {N}$
, let
$N,k_0,\in \mathbb {N}$
, let
 $$\begin{align*}\mathcal{A}_{N,k_0} = \Big\{\sigma = (I_k)_{k=1}^\infty\in[\mathcal{D}^+]: \sup_{T\in\mathscr{T}}\sum_{k=k_0}^\infty|a^T_{I_k} - a^T_{I_{k-1}}| \leq 2^{-N}\Big\},\end{align*}$$
$$\begin{align*}\mathcal{A}_{N,k_0} = \Big\{\sigma = (I_k)_{k=1}^\infty\in[\mathcal{D}^+]: \sup_{T\in\mathscr{T}}\sum_{k=k_0}^\infty|a^T_{I_k} - a^T_{I_{k-1}}| \leq 2^{-N}\Big\},\end{align*}$$
which is a closed subset of
![]() $[\mathcal {D}^+]$
, and by the claim, we have
$[\mathcal {D}^+]$
, and by the claim, we have
![]() $\cup _{k_0}\mathscr {A}_{N,k_0} = [\mathcal {D}^+]$
for all
$\cup _{k_0}\mathscr {A}_{N,k_0} = [\mathcal {D}^+]$
for all
![]() $N\!\in \!\mathbb {N}$
. We may therefore pick a strictly increasing sequence of natural numbers
$N\!\in \!\mathbb {N}$
. We may therefore pick a strictly increasing sequence of natural numbers
![]() $(k_N)$
so that for each N, we have
$(k_N)$
so that for each N, we have
![]() $|\mathscr {A}_{N,k_N}| \geq 1-\eta /2^N$
. We put
$|\mathscr {A}_{N,k_N}| \geq 1-\eta /2^N$
. We put
![]() $\mathscr {A} = \cap _N\mathscr {A}_{N,k_N}$
, and we demonstrate that this is the desired set.
$\mathscr {A} = \cap _N\mathscr {A}_{N,k_N}$
, and we demonstrate that this is the desired set.
To show that
![]() $\{TP_{\mathscr {A}}:T\in \mathscr {T}\}$
is relatively compact with respect to the operator norm, we fix
$\{TP_{\mathscr {A}}:T\in \mathscr {T}\}$
is relatively compact with respect to the operator norm, we fix
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $(T_n)_n$
in
$(T_n)_n$
in
![]() $\mathscr {T}$
. For each
$\mathscr {T}$
. For each
![]() $n\in \mathbb {N}$
, denote
$n\in \mathbb {N}$
, denote
![]() $D_n = D_{T_n}$
. We will find
$D_n = D_{T_n}$
. We will find
![]() $M\in [\mathbb {N}]^{\infty }$
so that for all
$M\in [\mathbb {N}]^{\infty }$
so that for all
![]() $n,m\in M$
, we have
$n,m\in M$
, we have
![]() $\|T_nP_{\mathscr {A}} - T_mP_{\mathscr {A}}\| \leq 11\varepsilon $
. Fix
$\|T_nP_{\mathscr {A}} - T_mP_{\mathscr {A}}\| \leq 11\varepsilon $
. Fix
![]() $N\in \mathbb {N}$
so that
$N\in \mathbb {N}$
so that
![]() $2^{-N}\leq \varepsilon $
,
$2^{-N}\leq \varepsilon $
,
![]() $\varepsilon _{k_N}\leq \varepsilon $
, and
$\varepsilon _{k_N}\leq \varepsilon $
, and
![]() $\delta _{k_N}\leq \varepsilon $
. For each
$\delta _{k_N}\leq \varepsilon $
. For each
![]() $n\in \mathbb {N}$
, write
$n\in \mathbb {N}$
, write
 $$ \begin{align*} T_n = D_nP_{(>k_N)} + \underbrace{(T_n-D_n)P_{(>k_N)}}_{=:A_n}+\underbrace{P_{(>k_N)}T_nP_{(\leq k_N)}}_{=:B_n} + \underbrace{P_{(\leq k_N)}T_nP_{(\leq k_N)}}_{=:C_n}. \end{align*} $$
$$ \begin{align*} T_n = D_nP_{(>k_N)} + \underbrace{(T_n-D_n)P_{(>k_N)}}_{=:A_n}+\underbrace{P_{(>k_N)}T_nP_{(\leq k_N)}}_{=:B_n} + \underbrace{P_{(\leq k_N)}T_nP_{(\leq k_N)}}_{=:C_n}. \end{align*} $$
Then we have
![]() $\|A_n\| \leq \varepsilon _{k_N}\leq \varepsilon $
and
$\|A_n\| \leq \varepsilon _{k_N}\leq \varepsilon $
and
![]() $\|B_n\| \leq \delta _{k_N}\leq \varepsilon $
. By passing to a subsequence of
$\|B_n\| \leq \delta _{k_N}\leq \varepsilon $
. By passing to a subsequence of
![]() $(T_n)$
, we may assume that for all
$(T_n)$
, we may assume that for all
![]() $n,m\in \mathbb {N}$
, we have (letting
$n,m\in \mathbb {N}$
, we have (letting
![]() $a_I^n=a^{T_n}_I$
)
$a_I^n=a^{T_n}_I$
)
 $$ \begin{align} \sum_{\left\{\substack{I\in\mathcal{D}^+\\|I|\geq 1/2^{k_N+1}}\right\}}|a_I^n - a_I^m| \leq \varepsilon. \end{align} $$
$$ \begin{align} \sum_{\left\{\substack{I\in\mathcal{D}^+\\|I|\geq 1/2^{k_N+1}}\right\}}|a_I^n - a_I^m| \leq \varepsilon. \end{align} $$
Since the
![]() $C_n$
are bounded elements of a finite-dimensional space, we can also assume that
$C_n$
are bounded elements of a finite-dimensional space, we can also assume that
![]() $\|C_n - C_m\| \leq \varepsilon $
, for
$\|C_n - C_m\| \leq \varepsilon $
, for
![]() $m,n\in \mathbb {N}$
. Therefore, for
$m,n\in \mathbb {N}$
. Therefore, for
![]() $n,m\in \mathbb {N}$
, we have
$n,m\in \mathbb {N}$
, we have
 $$ \begin{align*} \|T_nP_{\mathscr{A}} - T_mP_{\mathscr{A}}\| \leq \underbrace{\| D_nP_{(>k_N)}P_{\mathscr{A}} - D_mP_{(>k_N)}P_{\mathscr{A}} \|}_{=:\Lambda} + 5\varepsilon. \end{align*} $$
$$ \begin{align*} \|T_nP_{\mathscr{A}} - T_mP_{\mathscr{A}}\| \leq \underbrace{\| D_nP_{(>k_N)}P_{\mathscr{A}} - D_mP_{(>k_N)}P_{\mathscr{A}} \|}_{=:\Lambda} + 5\varepsilon. \end{align*} $$
Luckily, the remaining quantity
![]() $\Lambda $
is the norm of a Haar multiplier on
$\Lambda $
is the norm of a Haar multiplier on
![]() $L_1$
, and we know how to compute this. If for
$L_1$
, and we know how to compute this. If for
![]() $\sigma = (I_k)_{k=0}^\infty \in \mathscr {A}$
, we put
$\sigma = (I_k)_{k=0}^\infty \in \mathscr {A}$
, we put
 $$\begin{align*}\Lambda_\sigma &= \sum_{k=k_N+1}^\infty|(a^n_{I_k}-a^m_{I_k}) - (a^n_{I_{k-1}}-a^m_{I_{k-1}})| + |a^n_{I_{k_N}} - a^m_{I_{k_N}}| + \lim_k|a^n_{I_k}-a^m_{I_k}|\\&\leq 2\underbrace{\sum_{k=k_N+1}^\infty|(a^n_{I_k}-a^m_{I_k}) - (a^n_{I_{k-1}}-a^m_{I_{k-1}})|}_{\leq 2/2^N\leq 2\varepsilon} + 2\underbrace{|a^n_{I_{k_N}} - a^m_{I_{k_N}}|}_{\leq \varepsilon} \leq6\varepsilon. \end{align*}$$
$$\begin{align*}\Lambda_\sigma &= \sum_{k=k_N+1}^\infty|(a^n_{I_k}-a^m_{I_k}) - (a^n_{I_{k-1}}-a^m_{I_{k-1}})| + |a^n_{I_{k_N}} - a^m_{I_{k_N}}| + \lim_k|a^n_{I_k}-a^m_{I_k}|\\&\leq 2\underbrace{\sum_{k=k_N+1}^\infty|(a^n_{I_k}-a^m_{I_k}) - (a^n_{I_{k-1}}-a^m_{I_{k-1}})|}_{\leq 2/2^N\leq 2\varepsilon} + 2\underbrace{|a^n_{I_{k_N}} - a^m_{I_{k_N}}|}_{\leq \varepsilon} \leq6\varepsilon. \end{align*}$$
Then by Remark 2.8,
![]() $\Lambda = \sup _{\sigma \in \mathscr {A}}\Lambda _\sigma $
and thus
$\Lambda = \sup _{\sigma \in \mathscr {A}}\Lambda _\sigma $
and thus
![]() $\|T_nP_{\mathscr {A}} - T_mP_{\mathscr {A}}\|\leq 11\varepsilon $
.
$\|T_nP_{\mathscr {A}} - T_mP_{\mathscr {A}}\|\leq 11\varepsilon $
.
We now provide the required proof of the claim. We fix
![]() $\sigma = (I_k)_{k=0}^\infty $
, with associated signs
$\sigma = (I_k)_{k=0}^\infty $
, with associated signs
![]() $(\theta _k)_{k=0}^\infty $
. Let us assume that the conclusion fails. Then we may find
$(\theta _k)_{k=0}^\infty $
. Let us assume that the conclusion fails. Then we may find
![]() $(T_n)_n = (T^{(x^*_n,x_n)})_n$
in
$(T_n)_n = (T^{(x^*_n,x_n)})_n$
in
![]() $\mathscr {T}$
, each
$\mathscr {T}$
, each
![]() $T_n$
is associated with a
$T_n$
is associated with a
![]() $D_n$
(each
$D_n$
(each
![]() $D_n$
has entries
$D_n$
has entries
![]() $(a_I^n)_{I\in \mathcal {D}^+}$
) and
$(a_I^n)_{I\in \mathcal {D}^+}$
) and
![]() $k_1 < \ell _1<k_2<\ell _2<\cdots $
so that for all
$k_1 < \ell _1<k_2<\ell _2<\cdots $
so that for all
![]() $n\in \mathbb {N}$
$n\in \mathbb {N}$
 $$ \begin{align*} \sum_{k=k_n+1}^{\ell_n}|a^{n}_{I_k} - a^{n}_{I_{k-1}}|\geq r. \end{align*} $$
$$ \begin{align*} \sum_{k=k_n+1}^{\ell_n}|a^{n}_{I_k} - a^{n}_{I_{k-1}}|\geq r. \end{align*} $$
Pick
![]() $k_0\in \mathbb {N}$
so that
$k_0\in \mathbb {N}$
so that
![]() $\varepsilon _{k_0}\leq r/12$
. For
$\varepsilon _{k_0}\leq r/12$
. For
![]() $k,n\in \mathbb {N}$
define
$k,n\in \mathbb {N}$
define
![]() $b_k^n = 0$
if
$b_k^n = 0$
if
![]() $k\leq k_0$
and
$k\leq k_0$
and
![]() $b_k^n = a_{I_k}^{n}$
if
$b_k^n = a_{I_k}^{n}$
if
![]() $k>k_0$
. If we additionally assume that
$k>k_0$
. If we additionally assume that
![]() $k_1>k_0$
, then for all
$k_1>k_0$
, then for all
![]() $n\in \mathbb {N}$
, we have
$n\in \mathbb {N}$
, we have
 $$ \begin{align} \sum_{k=k_n+1}^{\ell_n}|b_k^n - b^n_{k-1}|\geq r. \end{align} $$
$$ \begin{align} \sum_{k=k_n+1}^{\ell_n}|b_k^n - b^n_{k-1}|\geq r. \end{align} $$
For each
![]() $n,\ell \in \mathbb {N}$
, put
$n,\ell \in \mathbb {N}$
, put
 $$\begin{align*}f_n^\ell = \sum_{k=0}^\ell b_k^n\theta_k|I_k|^{-1}h_{I_k} = D_nP_{(>k_0)}(\underbrace{|I_{\ell+1}|^{-1}\chi_{I_{\ell+1}}}_{=:\psi_\ell}).\end{align*}$$
$$\begin{align*}f_n^\ell = \sum_{k=0}^\ell b_k^n\theta_k|I_k|^{-1}h_{I_k} = D_nP_{(>k_0)}(\underbrace{|I_{\ell+1}|^{-1}\chi_{I_{\ell+1}}}_{=:\psi_\ell}).\end{align*}$$
By Lemma 3.6, we may find a sequence of
![]() $(A_n)_n$
of disjoint measurable sets so that for each
$(A_n)_n$
of disjoint measurable sets so that for each
![]() $n\in \mathbb {N}$
, the sequence
$n\in \mathbb {N}$
, the sequence
![]() $(f_n^\ell (s))_{\ell \geq \ell _n}$
is constant for all
$(f_n^\ell (s))_{\ell \geq \ell _n}$
is constant for all
![]() $s\in A_n$
and
$s\in A_n$
and
![]() $\|f_n^{\ell _n}|_{A_n}\|_{L_1} \geq r/3$
. For each
$\|f_n^{\ell _n}|_{A_n}\|_{L_1} \geq r/3$
. For each
![]() $n\in \mathbb {N}$
fix
$n\in \mathbb {N}$
fix
![]() $g_n$
in the unit sphere of
$g_n$
in the unit sphere of
![]() $L_\infty $
with support in
$L_\infty $
with support in
![]() $A_n$
so that for all
$A_n$
so that for all
![]() $\ell \geq \ell _n$
$\ell \geq \ell _n$
 $$ \begin{align*} r/3&\leq \|f_n^{\ell_n}|_{A_n}\|_{L_1} = \big|\langle g_n ,f_n^{\ell}\rangle\big| = \big|\langle g_n, D_nP_{(>k_0)}(\psi_\ell)\rangle\big|\\ \nonumber &\leq \big|\langle g_n, T_nP_{(>k_0)}(\psi_\ell)\rangle\big| + r/12 = \big|\langle g_n\otimes x_n^*, T\big(\underbrace{(P_{(>k_0)}\psi_\ell)}_{\phi_\ell}\otimes x_n\big)\rangle\big| + r/12. \end{align*} $$
$$ \begin{align*} r/3&\leq \|f_n^{\ell_n}|_{A_n}\|_{L_1} = \big|\langle g_n ,f_n^{\ell}\rangle\big| = \big|\langle g_n, D_nP_{(>k_0)}(\psi_\ell)\rangle\big|\\ \nonumber &\leq \big|\langle g_n, T_nP_{(>k_0)}(\psi_\ell)\rangle\big| + r/12 = \big|\langle g_n\otimes x_n^*, T\big(\underbrace{(P_{(>k_0)}\psi_\ell)}_{\phi_\ell}\otimes x_n\big)\rangle\big| + r/12. \end{align*} $$
Note that for all
![]() $\ell \in \mathbb {N}$
,
$\ell \in \mathbb {N}$
,
![]() $\|\phi _\ell \|_{L_1}\leq 2$
. Then for all
$\|\phi _\ell \|_{L_1}\leq 2$
. Then for all
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $\ell \geq \ell _n$
,
$\ell \geq \ell _n$
,
Pick an
![]() $L\in [\mathbb {N}]^\infty $
so that for each
$L\in [\mathbb {N}]^\infty $
so that for each
![]() $m,n\in \mathbb {N}$
, the limit
$m,n\in \mathbb {N}$
, the limit
Because the sequence
![]() $(g_m)_m$
is disjointly supported, an identical calculation as in equation (30) yields that for all
$(g_m)_m$
is disjointly supported, an identical calculation as in equation (30) yields that for all
![]() $n\in \mathbb {N}$
, we have
$n\in \mathbb {N}$
, we have
Thus, by Rosenthal’s Lemma 3.1, we may pass to a subsequence and relabel so that for all
![]() $n_0\in \mathbb {N}$
, we have
$n_0\in \mathbb {N}$
, we have
![]() $\sum _{m\neq n_0}|\xi _{n_0}(m)| \leq r/8$
.
$\sum _{m\neq n_0}|\xi _{n_0}(m)| \leq r/8$
.
We will show that
![]() $(x_n)_n$
must be equivalent to the unit vector basis of
$(x_n)_n$
must be equivalent to the unit vector basis of
![]() $\ell _1$
, which would contradict our assumption and thus finish the proof. Fix scalars
$\ell _1$
, which would contradict our assumption and thus finish the proof. Fix scalars
![]() $a_1,\ldots ,a_N$
, and for
$a_1,\ldots ,a_N$
, and for
![]() $\ell \in L$
with
$\ell \in L$
with
![]() $\ell \geq \ell _N$
pick appropriate scalars
$\ell \geq \ell _N$
pick appropriate scalars
![]() $\zeta ^\ell _1,\ldots ,\zeta ^\ell _N$
of modulus one so that we have
$\zeta ^\ell _1,\ldots ,\zeta ^\ell _N$
of modulus one so that we have
 $$\begin{align*}\frac{r}{4}\sum_{n=1}^N|a_n| \leq \sum_{n=1}^N\langle g_n\otimes\big(\zeta^\ell_nx_n^*\big), T\big(\phi_\ell\otimes(a_nx_n)\big)\rangle \end{align*}$$
$$\begin{align*}\frac{r}{4}\sum_{n=1}^N|a_n| \leq \sum_{n=1}^N\langle g_n\otimes\big(\zeta^\ell_nx_n^*\big), T\big(\phi_\ell\otimes(a_nx_n)\big)\rangle \end{align*}$$
and put
 $$ \begin{align*} \Lambda_\ell &= \big|\big\langle\sum_{m=1}^N g_n\otimes\big(\zeta^\ell_mx_m^*\big),\sum_{n=1}^NT\big(\phi_\ell\otimes(\sum_{n=1}^Na_nx_n)\big)\big\rangle\big|\\ &\leq \Big(2\|T\|\sup_{x^*\in A}\|x^*\|\Big)\big\|\sum_{n=1}^N a_nx_n\big\|. \end{align*} $$
$$ \begin{align*} \Lambda_\ell &= \big|\big\langle\sum_{m=1}^N g_n\otimes\big(\zeta^\ell_mx_m^*\big),\sum_{n=1}^NT\big(\phi_\ell\otimes(\sum_{n=1}^Na_nx_n)\big)\big\rangle\big|\\ &\leq \Big(2\|T\|\sup_{x^*\in A}\|x^*\|\Big)\big\|\sum_{n=1}^N a_nx_n\big\|. \end{align*} $$
But also,
 $$ \begin{align*} \lim_{\ell\in L}\Lambda_\ell &= \lim_{\ell\in L}\Big| \sum_{n=1}^N\langle g_n\otimes\big(\zeta^\ell_nx_n^*\big), T\big(\phi_\ell\otimes(a_nx_n)\big)\rangle\\ &\quad + \sum_{n=1}^Na_n\sum_{m\neq n}\zeta_m^\ell \langle g_m\otimes x_m^*, T\big(\psi_\ell\otimes x_n\big) \rangle\Big|\\ &\geq \frac{r}{4}\sum_{n=1}^N|a_n| - \sum_{n=1}^N|a_n|\sum_{m\neq n}|\xi_n(m)| \geq \frac{r}{8}\sum_{n=1}^N|a_n|. \end{align*} $$
$$ \begin{align*} \lim_{\ell\in L}\Lambda_\ell &= \lim_{\ell\in L}\Big| \sum_{n=1}^N\langle g_n\otimes\big(\zeta^\ell_nx_n^*\big), T\big(\phi_\ell\otimes(a_nx_n)\big)\rangle\\ &\quad + \sum_{n=1}^Na_n\sum_{m\neq n}\zeta_m^\ell \langle g_m\otimes x_m^*, T\big(\psi_\ell\otimes x_n\big) \rangle\Big|\\ &\geq \frac{r}{4}\sum_{n=1}^N|a_n| - \sum_{n=1}^N|a_n|\sum_{m\neq n}|\xi_n(m)| \geq \frac{r}{8}\sum_{n=1}^N|a_n|. \end{align*} $$
Therefore,
![]() $\|\sum _{n=1}^Na_nx_n\| \geq r/(16\|T\|\sup _{x^*\in A}\|x^*\|)\sum _{n=1}^N|a_n|$
.
$\|\sum _{n=1}^Na_nx_n\| \geq r/(16\|T\|\sup _{x^*\in A}\|x^*\|)\sum _{n=1}^N|a_n|$
.
4 Projectional factors of X-diagonal operators
The main purpose of the section is to prove the following first step towards the final result. The Fundamental Lemma (Theorem 3.4) is a necessary part of the proof.
Theorem 4.1. Let X be in
![]() $\mathcal H^*$
, and let
$\mathcal H^*$
, and let
![]() $T:L_1(X)\to L_1(X)$
be a bounded linear operator. Then for every
$T:L_1(X)\to L_1(X)$
be a bounded linear operator. Then for every
![]() $\varepsilon>0$
, T is a
$\varepsilon>0$
, T is a
![]() $1$
-projectional factor with error
$1$
-projectional factor with error
![]() $\varepsilon $
of an X-diagonal operator
$\varepsilon $
of an X-diagonal operator
![]() $S:L_1(X)\to L_1(X)$
.
$S:L_1(X)\to L_1(X)$
.
The strategy is to first pass to an operator S with the family
![]() $(S^{(L,M)})_{L\neq M}$
uniformly eventually close to Haar multipliers (in reality, S satisfies something slightly stronger). We will then use the Fundamental Lemma to eliminate these entries. The following result states how uniform eventual proximity to Haar multipliers is achieved in practice.
$(S^{(L,M)})_{L\neq M}$
uniformly eventually close to Haar multipliers (in reality, S satisfies something slightly stronger). We will then use the Fundamental Lemma to eliminate these entries. The following result states how uniform eventual proximity to Haar multipliers is achieved in practice.
Lemma 4.2. Let
![]() $\mathscr {T}$
be a subset of
$\mathscr {T}$
be a subset of
![]() $\mathcal {L}(L_1)$
and
$\mathcal {L}(L_1)$
and
![]() $(\varepsilon _{(I,J)})_{(I,J)\in \mathcal {D}^+\times \mathcal {D}^+}$
be a summable collection of positive real numbers. If for every
$(\varepsilon _{(I,J)})_{(I,J)\in \mathcal {D}^+\times \mathcal {D}^+}$
be a summable collection of positive real numbers. If for every
![]() $I\neq J\in \mathcal {D}^+$
and
$I\neq J\in \mathcal {D}^+$
and
![]() $T\in \mathscr {T}$
, we have
$T\in \mathscr {T}$
, we have
![]() $\big |\langle h_I, T\big (|J|^{-1}h_J\big )\rangle \big |\leq \varepsilon _{(I,J)}$
, then
$\big |\langle h_I, T\big (|J|^{-1}h_J\big )\rangle \big |\leq \varepsilon _{(I,J)}$
, then
![]() $\mathscr {T}$
is uniformly eventually close to Haar multipliers.
$\mathscr {T}$
is uniformly eventually close to Haar multipliers.
Proof. For fixed
![]() $T\in \mathscr {T}$
, put
$T\in \mathscr {T}$
, put
![]() $a_I = \langle h_I, T(|I^{-1}|h_I)\rangle $
. This collection defines a bounded Haar multiplier
$a_I = \langle h_I, T(|I^{-1}|h_I)\rangle $
. This collection defines a bounded Haar multiplier
![]() $D_T$
because for all f in the unit ball of
$D_T$
because for all f in the unit ball of
![]() $L_1$
,
$L_1$
,
![]() $\|(T-D_T)f\| \leq \sum _{I\in \mathcal {D}^+}\sum _{\{J\in \mathcal {D}^+: J\neq I\}}|\langle h_I,T(|J|^{-1}h_J)\rangle | <\infty $
. Also, for all
$\|(T-D_T)f\| \leq \sum _{I\in \mathcal {D}^+}\sum _{\{J\in \mathcal {D}^+: J\neq I\}}|\langle h_I,T(|J|^{-1}h_J)\rangle | <\infty $
. Also, for all
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
 $$ \begin{align*} \Big\|TP_{(>n)} - D_TP_{(>n)}\Big\|& \leq \sum_{I\in\mathcal{D}^+}\sum_{J\in\mathcal{D}^+\setminus\mathcal{D}^n}\varepsilon_{(I,J)} =:\varepsilon_n\text{ and}\\ \Big\|P_{(>n)} T - P_{(>n)}D_T\Big\| & \leq \sum_{I\in\mathcal{D}^+\setminus\mathcal{D}^n}\sum_{J\in\mathcal{D}^+}\varepsilon_{(I,J)} =:\delta_n. \end{align*} $$
$$ \begin{align*} \Big\|TP_{(>n)} - D_TP_{(>n)}\Big\|& \leq \sum_{I\in\mathcal{D}^+}\sum_{J\in\mathcal{D}^+\setminus\mathcal{D}^n}\varepsilon_{(I,J)} =:\varepsilon_n\text{ and}\\ \Big\|P_{(>n)} T - P_{(>n)}D_T\Big\| & \leq \sum_{I\in\mathcal{D}^+\setminus\mathcal{D}^n}\sum_{J\in\mathcal{D}^+}\varepsilon_{(I,J)} =:\delta_n. \end{align*} $$
Both
![]() $(\varepsilon _n)_n$
and
$(\varepsilon _n)_n$
and
![]() $(\delta _n)_n$
tend to zero.
$(\delta _n)_n$
tend to zero.
The next lemma is the basic tool used to achieve the first step.
Lemma 4.3. Let X be in
![]() $\mathcal H^*$
and
$\mathcal H^*$
and
![]() $\mathscr {T}\subset \mathcal {L}(X)$
,
$\mathscr {T}\subset \mathcal {L}(X)$
,
![]() $G\subset X^*$
and
$G\subset X^*$
and
![]() $F\subset X$
be finite sets. Then for any
$F\subset X$
be finite sets. Then for any
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $i_0\in \mathbb {N}$
so that for any disjoint collection
$i_0\in \mathbb {N}$
so that for any disjoint collection
![]() $\Delta $
of
$\Delta $
of
![]() $\mathcal {D}^+$
with
$\mathcal {D}^+$
with
![]() $\min \iota (\Delta )\geq i_0$
and any
$\min \iota (\Delta )\geq i_0$
and any
![]() $\theta \in \{-1,1\}^\Delta $
, we have
$\theta \in \{-1,1\}^\Delta $
, we have
(recall that
![]() $h^{\theta }_\Delta $
was introduced before Definition 2.10).
$h^{\theta }_\Delta $
was introduced before Definition 2.10).
Proof. The result is an immediate consequence of the following fact: let
![]() $(\Delta _k)$
be a sequence of finite disjoint collections of
$(\Delta _k)$
be a sequence of finite disjoint collections of
![]() $\mathcal {D}^+$
with
$\mathcal {D}^+$
with
![]() $\lim _k\min \iota (\Delta _k) = \infty $
, and for every
$\lim _k\min \iota (\Delta _k) = \infty $
, and for every
![]() $k\in \mathbb {N}$
let
$k\in \mathbb {N}$
let
![]() $\theta _k\in \{-1,1\}^{\Delta _k}$
.
$\theta _k\in \{-1,1\}^{\Delta _k}$
.
-
(a) The sequence
 $(h_{\Delta _k}^{\theta _k})_k$
is weakly null.
$(h_{\Delta _k}^{\theta _k})_k$
is weakly null. -
(b) The sequence
 $(h_{\Delta _k}^{\theta _k})_k$
is a bounded block sequence in
$(h_{\Delta _k}^{\theta _k})_k$
is a bounded block sequence in
 $X^*$
and thus is
$X^*$
and thus is
 $w^*$
-null.
$w^*$
-null.
There is nothing further to say about statement (b). We now explain how statement (a) is achieved. Note that any sequence of independent
![]() $\{-1,1\}$
-valued random variables of mean
$\{-1,1\}$
-valued random variables of mean
![]() $0$
is distributionally equivalent to
$0$
is distributionally equivalent to
![]() $(r_n)_n$
and thus weakly null. Any sequence as in statement (a) has a subsequence that is of the form
$(r_n)_n$
and thus weakly null. Any sequence as in statement (a) has a subsequence that is of the form
![]() $(\frac {r_n+r^{\prime }_n}2)$
, where
$(\frac {r_n+r^{\prime }_n}2)$
, where
![]() $(r_n)$
and
$(r_n)$
and
![]() $(r^{\prime }_n)$
are both sequences of independent
$(r^{\prime }_n)$
are both sequences of independent
![]() $\{-1,1\}$
-valued random variables of mean
$\{-1,1\}$
-valued random variables of mean
![]() $0$
. Thus, it is weakly null as well.
$0$
. Thus, it is weakly null as well.
We carry out the first step towards the proof of Theorem 4.1
Proposition 4.4. Let X be in
![]() $\mathcal H^{*}$
, and denote by C the set of all pairs
$\mathcal H^{*}$
, and denote by C the set of all pairs
![]() $(g,f)$
in
$(g,f)$
in
![]() $B_{X^*}\times B_X$
so that g and f have finite and disjoint supports with respect to the Haar system. Then every bounded linear operator
$B_{X^*}\times B_X$
so that g and f have finite and disjoint supports with respect to the Haar system. Then every bounded linear operator
![]() $T:L_1(X)\to L_1(X)$
is a 1-projectional factor of a bounded linear operator
$T:L_1(X)\to L_1(X)$
is a 1-projectional factor of a bounded linear operator
![]() $S:L_1(X) \to L_1(X)$
so that the family
$S:L_1(X) \to L_1(X)$
so that the family
![]() $\{S^{(f,g)}:(f,g)\in C\}$
is uniformly eventually close to Haar multipliers.
$\{S^{(f,g)}:(f,g)\in C\}$
is uniformly eventually close to Haar multipliers.
Proof. We will inductively construct faithful Haar systems
![]() $(\widetilde h_I)_{I\in \mathcal {D}^+}$
and
$(\widetilde h_I)_{I\in \mathcal {D}^+}$
and
![]() $(\widehat h_L)_{L\in \mathcal {D}^+}$
. In each step k of the induction, we will define
$(\widehat h_L)_{L\in \mathcal {D}^+}$
. In each step k of the induction, we will define
![]() $\widetilde h_I$
and then
$\widetilde h_I$
and then
![]() $\widehat h_L$
with
$\widehat h_L$
with
![]() $k = \iota (I) = \iota (L)$
(i.e.,
$k = \iota (I) = \iota (L)$
(i.e.,
![]() $I=L$
, but we separate the notation for clarity). These vectors are of the form
$I=L$
, but we separate the notation for clarity). These vectors are of the form
![]() $\widetilde h_I = \sum _{J\in \Delta _I}h_J$
and
$\widetilde h_I = \sum _{J\in \Delta _I}h_J$
and
![]() $\widehat h_L = \sum _{M\in \Gamma _L}h_M$
. The inductive assumption is the following.
$\widehat h_L = \sum _{M\in \Gamma _L}h_M$
. The inductive assumption is the following.
For every
![]() $J,J',M,M'\in \mathcal {D}^+$
with
$J,J',M,M'\in \mathcal {D}^+$
with
![]() $\iota (J') \neq \iota (J)\leq k$
and
$\iota (J') \neq \iota (J)\leq k$
and
![]() $\iota (M')\neq \iota (M)\leq k$
, we have
$\iota (M')\neq \iota (M)\leq k$
, we have
We may start by picking
![]() $\widetilde h_\emptyset = \widehat h_\emptyset = h_\emptyset $
. We now carry out the kth inductive step. Let
$\widetilde h_\emptyset = \widehat h_\emptyset = h_\emptyset $
. We now carry out the kth inductive step. Let
![]() $I = L\in \mathcal {D}^+$
with
$I = L\in \mathcal {D}^+$
with
![]() $\iota (I) = \iota (L) = k$
. We will apply Lemma 4.3 twice, once for
$\iota (I) = \iota (L) = k$
. We will apply Lemma 4.3 twice, once for
![]() $L_1$
and once for X. First, define the following finite sets:
$L_1$
and once for X. First, define the following finite sets:
 $$ \begin{align*} \mathscr{T}_1 = \{T^{(\nu_{M}\widehat h_{M},\mu_{M'}\widehat h_{M'})}:\iota(M),\iota(M')<k\}\subset\mathcal{L}(L_1)\\ G_1 = \{\widetilde h_J: \iota(J)<k\}\subset (L_1)^* \text{ and }F_1 = \{|J|\widetilde h_J: \iota(J)<k\}\subset L_1. \end{align*} $$
$$ \begin{align*} \mathscr{T}_1 = \{T^{(\nu_{M}\widehat h_{M},\mu_{M'}\widehat h_{M'})}:\iota(M),\iota(M')<k\}\subset\mathcal{L}(L_1)\\ G_1 = \{\widetilde h_J: \iota(J)<k\}\subset (L_1)^* \text{ and }F_1 = \{|J|\widetilde h_J: \iota(J)<k\}\subset L_1. \end{align*} $$
Use Lemma 4.3 to pick
![]() $\widetilde h_I$
so that
$\widetilde h_I$
so that
Next, we take the finite sets
 $$ \begin{align*} \mathscr{T}_2 = \{T_{(\widetilde h_{J},|J'|^{-1}\widetilde h_{J'})}:\iota(J),\iota(J')\leq k\}\subset\mathcal{L}(X)\\ G_2 = \{ \nu_M\widehat h_M: \iota(M)<k\}\subset (L_1)^* \text{ and }F_2 = \{\mu_M\widehat h_M: \iota(M)<k\}\subset X. \end{align*} $$
$$ \begin{align*} \mathscr{T}_2 = \{T_{(\widetilde h_{J},|J'|^{-1}\widetilde h_{J'})}:\iota(J),\iota(J')\leq k\}\subset\mathcal{L}(X)\\ G_2 = \{ \nu_M\widehat h_M: \iota(M)<k\}\subset (L_1)^* \text{ and }F_2 = \{\mu_M\widehat h_M: \iota(M)<k\}\subset X. \end{align*} $$
Use Lemma 4.3 to pick
![]() $\widehat h_M$
so that
$\widehat h_M$
so that
The inductive step is complete, and it is straightforward to check that the inductive hypothesis is preserved.
Take the operator S given in Example 2.17. We will show that it has the desired property. Fix
![]() $g\in B_{X^*}$
,
$g\in B_{X^*}$
,
![]() $f\in B_X$
with
$f\in B_X$
with
![]() $g = \sum _{M\in E}b_M\nu _M h_M$
and
$g = \sum _{M\in E}b_M\nu _M h_M$
and
![]() $f = \sum _{M\in F}a_M\mu _Mh_M$
so that
$f = \sum _{M\in F}a_M\mu _Mh_M$
so that
![]() $F,G$
are finite and disjoint. Then
$F,G$
are finite and disjoint. Then
and for
![]() $I\neq J\in \mathcal {D}^+$
, we have
$I\neq J\in \mathcal {D}^+$
, we have
 $$ \begin{align*}\big|\big\langle h_I , S^{(g,f)}(|J|^{-1}h_J) \big\rangle\big|&\leq \sum_{M\in E}\sum_{M'\in F}\big|\big\langle h_I , S^{(M,M')}(|J|^{-1}h_J) \big\rangle\big|\\&= \sum_{M\in E}\sum_{M'\in F}\big|\big\langle h_I\otimes(\nu_Mh_M) , S\big((|J|^{-1}h_J)\otimes(\mu_{M'}h_{M'})\big) \big\rangle\big|\\&= \sum_{M\in E}\sum_{M'\in F}\big|\big\langle\widetilde h_I\otimes(\nu_M\widehat h_M) , T\big((|J|^{-1}\widetilde h_J)\otimes(\mu_{M'}\widehat h_{M'})\big) \big\rangle\big|\\&\leq \sum_{M\in E}\sum_{M'\in F}2^{-(\iota(J)+\iota(J')+\iota(M)+\iota(M'))}\leq 2^{-(\iota(I)+\iota(J))}=:\varepsilon_{(I,J)}. \end{align*} $$
$$ \begin{align*}\big|\big\langle h_I , S^{(g,f)}(|J|^{-1}h_J) \big\rangle\big|&\leq \sum_{M\in E}\sum_{M'\in F}\big|\big\langle h_I , S^{(M,M')}(|J|^{-1}h_J) \big\rangle\big|\\&= \sum_{M\in E}\sum_{M'\in F}\big|\big\langle h_I\otimes(\nu_Mh_M) , S\big((|J|^{-1}h_J)\otimes(\mu_{M'}h_{M'})\big) \big\rangle\big|\\&= \sum_{M\in E}\sum_{M'\in F}\big|\big\langle\widetilde h_I\otimes(\nu_M\widehat h_M) , T\big((|J|^{-1}\widetilde h_J)\otimes(\mu_{M'}\widehat h_{M'})\big) \big\rangle\big|\\&\leq \sum_{M\in E}\sum_{M'\in F}2^{-(\iota(J)+\iota(J')+\iota(M)+\iota(M'))}\leq 2^{-(\iota(I)+\iota(J))}=:\varepsilon_{(I,J)}. \end{align*} $$
By Lemma 4.2, the family under consideration is uniformly eventually close to Haar multipliers.
Remark 4.5. Proposition 4.4 can be achieved if we merely assume that X is a Haar system space, as condition (
![]() $\star $
) of Definition 2.14 can be replaced with a probabilistic argument. We presented the slightly simpler proof that assumes (
$\star $
) of Definition 2.14 can be replaced with a probabilistic argument. We presented the slightly simpler proof that assumes (
![]() $\star $
).
$\star $
).
We now eliminate the off-diagonal entries to obtain an X-diagonal operator that projectionally factors through T.
Proof of Theorem 4.1
By Proposition 4.4, T is a 1-projectional factor of an
![]() $S:L_1(X)\to L_1(X)$
that satisfies condition (ii) of Theorem 3.4.
$S:L_1(X)\to L_1(X)$
that satisfies condition (ii) of Theorem 3.4.
For a finite pairwise disjoint collection
![]() $\Gamma \subset \mathcal D^+$
, we define
$\Gamma \subset \mathcal D^+$
, we define
![]() $\Gamma (n)=\{ D\in \mathcal D_n: D\subset \Gamma ^* \}$
. Note that
$\Gamma (n)=\{ D\in \mathcal D_n: D\subset \Gamma ^* \}$
. Note that
![]() $\Gamma (n) $
is a partition of
$\Gamma (n) $
is a partition of
![]() $\Gamma ^*$
for large enough n. Also note that from our condition
$\Gamma ^*$
for large enough n. Also note that from our condition
![]() $(*)$
it follows that for two finite subsets
$(*)$
it follows that for two finite subsets
![]() $\Gamma ,\Gamma '$
of
$\Gamma ,\Gamma '$
of
![]() $\mathcal D$
, with
$\mathcal D$
, with
![]() $\Gamma ^*\cap (\Gamma ')^*=\emptyset $
, the set
$\Gamma ^*\cap (\Gamma ')^*=\emptyset $
, the set
satisfies condition (i) of Theorem 3.4. The following claim will be the main step towards recursively defining an appropriate faithful Haar system
![]() $(\tilde h_L)$
.
$(\tilde h_L)$
.
Claim. There are
![]() $\mathscr {A}\subset [\mathcal D]$
, with
$\mathscr {A}\subset [\mathcal D]$
, with
![]() $|\mathscr {A}|>1 -\eta $
, and
$|\mathscr {A}|>1 -\eta $
, and
![]() $\mathscr {U}\in [\mathbb {N}]^\infty $
, so that
$\mathscr {U}\in [\mathbb {N}]^\infty $
, so that
with respect to the operator norm, for all
![]() $\Gamma ,\Gamma '\subset \mathcal D$
, with
$\Gamma ,\Gamma '\subset \mathcal D$
, with
![]() $\Gamma ^*\cap (\Gamma ')^*=\emptyset $
.
$\Gamma ^*\cap (\Gamma ')^*=\emptyset $
.
To show the claim, we choose for each pair
![]() $(\Gamma ,\Gamma ')$
, with
$(\Gamma ,\Gamma ')$
, with
![]() $\Gamma ,\Gamma '\subset \mathcal D$
being finite,
$\Gamma ,\Gamma '\subset \mathcal D$
being finite,
![]() $\eta _{(\Gamma ,\Gamma ')}>0$
. with
$\eta _{(\Gamma ,\Gamma ')}>0$
. with
![]() $\sum \eta _{(\Gamma ,\Gamma ')}<\eta $
. Then, using Theorem 3.4, we choose a closed set
$\sum \eta _{(\Gamma ,\Gamma ')}<\eta $
. Then, using Theorem 3.4, we choose a closed set
![]() $\mathscr {A}_{(\Gamma ,\Gamma ')}$
in
$\mathscr {A}_{(\Gamma ,\Gamma ')}$
in
![]() $[\mathcal {D}^+]$
with
$[\mathcal {D}^+]$
with
![]() $|\mathscr {A}_{(\Gamma ,\Gamma ')}|> 1-\eta _{(\Gamma ,\Gamma ')}$
, so that
$|\mathscr {A}_{(\Gamma ,\Gamma ')}|> 1-\eta _{(\Gamma ,\Gamma ')}$
, so that
![]() $\{S^{(g,f)}P_{\mathscr {A}_{(\Gamma ,\Gamma ')}}:(g,f)\in C^{(\Gamma ,\Gamma ')}\}$
is relatively compact in the operator norm topology. Put
$\{S^{(g,f)}P_{\mathscr {A}_{(\Gamma ,\Gamma ')}}:(g,f)\in C^{(\Gamma ,\Gamma ')}\}$
is relatively compact in the operator norm topology. Put
![]() $\mathscr {A} = \cap \mathscr {A}_{(\Gamma ,\Gamma ')}$
, and note that
$\mathscr {A} = \cap \mathscr {A}_{(\Gamma ,\Gamma ')}$
, and note that
![]() $|\mathscr {A}|>1-\eta $
and that for each
$|\mathscr {A}|>1-\eta $
and that for each
![]() $(\Gamma ,\Gamma ')$
, we still have that
$(\Gamma ,\Gamma ')$
, we still have that
![]() $\{S^{(g,f)}P_{\mathscr {A}}:(g,f)\in C^{(\Gamma ,\Gamma ')}\}$
is relatively compact.
$\{S^{(g,f)}P_{\mathscr {A}}:(g,f)\in C^{(\Gamma ,\Gamma ')}\}$
is relatively compact.
Via a Cantor diagonalisation, find
![]() $\mathscr {U}\in [\mathbb {N}]^\infty $
so that for every pair
$\mathscr {U}\in [\mathbb {N}]^\infty $
so that for every pair
![]() $(\Gamma ,\Gamma ')$
, both limits
$(\Gamma ,\Gamma ')$
, both limits
exist with respect to the operator norm. As we see right away,
![]() $S^{(\Gamma ,\Gamma ')}_1 = S^{(\Gamma ,\Gamma ')}_2 = 0$
. Indeed, for any
$S^{(\Gamma ,\Gamma ')}_1 = S^{(\Gamma ,\Gamma ')}_2 = 0$
. Indeed, for any
![]() $g\in L_\infty $
and
$g\in L_\infty $
and
![]() $f\in L_1$
, we have
$f\in L_1$
, we have
 $$ \begin{align*} \langle g, S^{(\Gamma,\Gamma')}_2f\rangle &= \lim_{n\in\mathscr{U}} \big\langle g, S^{(\nu_{\Gamma^*} h_{\Gamma}, \mu_{(\Gamma')^*} h_{\Gamma'(n)})}\big(P_{\mathscr{A}}f)\big)\big\rangle\\ &= \lim_{n\in\mathscr{U}} \big\langle g\otimes (\nu_{\Gamma^*}h_\Gamma), S\big((P_{\mathscr{A}}f)\otimes (\mu_{(\Gamma')^*}h_{\Gamma'(n)})\big)\big\rangle = 0 \end{align*} $$
$$ \begin{align*} \langle g, S^{(\Gamma,\Gamma')}_2f\rangle &= \lim_{n\in\mathscr{U}} \big\langle g, S^{(\nu_{\Gamma^*} h_{\Gamma}, \mu_{(\Gamma')^*} h_{\Gamma'(n)})}\big(P_{\mathscr{A}}f)\big)\big\rangle\\ &= \lim_{n\in\mathscr{U}} \big\langle g\otimes (\nu_{\Gamma^*}h_\Gamma), S\big((P_{\mathscr{A}}f)\otimes (\mu_{(\Gamma')^*}h_{\Gamma'(n)})\big)\big\rangle = 0 \end{align*} $$
because
![]() $(h_{\Gamma '(n)})_n$
is weakly null in X, by Lemma 4.3. With the same computation,
$(h_{\Gamma '(n)})_n$
is weakly null in X, by Lemma 4.3. With the same computation,
![]() $S^{(\Gamma ,\Gamma ')}_2 = 0$
because
$S^{(\Gamma ,\Gamma ')}_2 = 0$
because
![]() $(h_{\Gamma '(n)})_n$
is
$(h_{\Gamma '(n)})_n$
is
![]() $w^*$
-null in
$w^*$
-null in
![]() $X^*$
. This finishes the proof of the claim.
$X^*$
. This finishes the proof of the claim.
We now choose inductively a faithful Haar system
![]() $(\widetilde h_L)_{L\in \mathcal {D}^+}$
so that for every
$(\widetilde h_L)_{L\in \mathcal {D}^+}$
so that for every
![]() $L\neq M\in \mathcal {D}^+$
, we have
$L\neq M\in \mathcal {D}^+$
, we have
Assume
![]() $M\in \mathcal D$
, and
$M\in \mathcal D$
, and
![]() $\widetilde h_L= h_{\Gamma _L}$
has been chosen for all
$\widetilde h_L= h_{\Gamma _L}$
has been chosen for all
![]() $L\in \mathcal D^+$
with
$L\in \mathcal D^+$
with
![]() $\iota (L)<\iota (M)$
, (
$\iota (L)<\iota (M)$
, (
![]() $\widetilde h_\emptyset = h_\emptyset $
and
$\widetilde h_\emptyset = h_\emptyset $
and
![]() $\widetilde h_{(0,1)}= h_{[0,1)}$
by definition). Without loss of generality, we can assume that
$\widetilde h_{(0,1)}= h_{[0,1)}$
by definition). Without loss of generality, we can assume that
![]() $M=K^+$
for some
$M=K^+$
for some
![]() $K\in \mathcal D$
with
$K\in \mathcal D$
with
![]() $\iota ( K)<\iota (M) $
. Thus we will choose
$\iota ( K)<\iota (M) $
. Thus we will choose
![]() $\Gamma _M$
so that
$\Gamma _M$
so that
![]() $\Gamma ^*_M= [\widetilde h_K=1]$
. For large enough
$\Gamma ^*_M= [\widetilde h_K=1]$
. For large enough
![]() $n_0\in \mathbb {N}$
, it follows that
$n_0\in \mathbb {N}$
, it follows that
![]() $[\widetilde h_K=1] =(\Gamma ' )^* $
for some
$[\widetilde h_K=1] =(\Gamma ' )^* $
for some
![]() $\Gamma '\subset \mathcal D_{n_0}$
. Then we can use our claim that for large enough
$\Gamma '\subset \mathcal D_{n_0}$
. Then we can use our claim that for large enough
![]() $n>0$
, we let
$n>0$
, we let
![]() $\Gamma _M= \Gamma '(n)$
. We deduce equation (37) for all
$\Gamma _M= \Gamma '(n)$
. We deduce equation (37) for all
![]() $L\in \mathcal D$
, with
$L\in \mathcal D$
, with
![]() $\iota (L)<\iota (M)$
$\iota (L)<\iota (M)$
Apply Proposition 2.18 to find a subspace Z of
![]() $Y_{\mathscr {A}}$
(i.e., in the image of
$Y_{\mathscr {A}}$
(i.e., in the image of
![]() $P_{\mathscr {A}}$
) that is 1-complemented in
$P_{\mathscr {A}}$
) that is 1-complemented in
![]() $L_1$
via
$L_1$
via
![]() $P:L_1\to Z$
and isometrically isomorphic to
$P:L_1\to Z$
and isometrically isomorphic to
![]() $L_1$
via
$L_1$
via
![]() $A:L_1\to Z$
. Let also W be the closed linear span of
$A:L_1\to Z$
. Let also W be the closed linear span of
![]() $(\widetilde h_L)_{L\in \mathcal {D}^+}$
in X,
$(\widetilde h_L)_{L\in \mathcal {D}^+}$
in X,
![]() $Q:X\to W$
be the canonical 1-projection and
$Q:X\to W$
be the canonical 1-projection and
![]() $B:X\to W$
be the canonical onto isometry.
$B:X\to W$
be the canonical onto isometry.
By Proposition 2.16, the operator
![]() $R = ((A^{-1}P)\otimes (B^{-1}Q))S(A\otimes B)$
is a 1-projectional factor of S and thus also of T. It remains to see that R is
$R = ((A^{-1}P)\otimes (B^{-1}Q))S(A\otimes B)$
is a 1-projectional factor of S and thus also of T. It remains to see that R is
![]() $\varepsilon $
-close to an X-diagonal operator. Fix
$\varepsilon $
-close to an X-diagonal operator. Fix
![]() $L\neq M$
. To compute the norm of
$L\neq M$
. To compute the norm of
![]() $R^{(L,M)}$
, we also fix
$R^{(L,M)}$
, we also fix
![]() $g\in B_{L_\infty }$
and
$g\in B_{L_\infty }$
and
![]() $f\in B_{L_1}$
.
$f\in B_{L_1}$
.
 $$ \begin{align*} \big|\big\langle g, R^{(L,M)} f\big\rangle\big| &= \big|\big\langle g\otimes(\nu_Lh_L), R (f\otimes\mu_Mh_M)\big\rangle\big|\\ &= \big|\big\langle \underbrace{P^*A^{-1*}g}_{:=v\in B_{L_\infty}}\otimes\underbrace{(Q^*B^{-1*}\nu_Lh_L)}_{=\nu_L\widetilde h_L}, S (\!\!\!\!\!\underbrace{Af}_{=: u\in B_{Y_{\mathscr{A}}}}\!\!\!\!\otimes \underbrace{B\mu_Mh_M}_{=\mu_M\widetilde h_M})\big\rangle\big|\\ & = \big|\big\langle v, S^{(\nu_L\widetilde h_L,\mu_M\widetilde h_M)} (P_{\mathscr{A}}u)\big\rangle\big| \leq \varepsilon 2^{-(\iota(L)+\iota(M))}. \end{align*} $$
$$ \begin{align*} \big|\big\langle g, R^{(L,M)} f\big\rangle\big| &= \big|\big\langle g\otimes(\nu_Lh_L), R (f\otimes\mu_Mh_M)\big\rangle\big|\\ &= \big|\big\langle \underbrace{P^*A^{-1*}g}_{:=v\in B_{L_\infty}}\otimes\underbrace{(Q^*B^{-1*}\nu_Lh_L)}_{=\nu_L\widetilde h_L}, S (\!\!\!\!\!\underbrace{Af}_{=: u\in B_{Y_{\mathscr{A}}}}\!\!\!\!\otimes \underbrace{B\mu_Mh_M}_{=\mu_M\widetilde h_M})\big\rangle\big|\\ & = \big|\big\langle v, S^{(\nu_L\widetilde h_L,\mu_M\widetilde h_M)} (P_{\mathscr{A}}u)\big\rangle\big| \leq \varepsilon 2^{-(\iota(L)+\iota(M))}. \end{align*} $$
By Remark 2.22, R is
![]() $\varepsilon $
-close to an X-diagonal operator.
$\varepsilon $
-close to an X-diagonal operator.
5 Stabilising entries of X-diagonal operators
Once we have an X-diagonal operator at hand, we can pass to another X-diagonal operator whose entries are stable in an extremely strong sense.
Theorem 5.1. Let X be in
![]() $\mathcal H^{**}$
, and let
$\mathcal H^{**}$
, and let
![]() $T:L_1(X)\to L_1(X)$
be a bounded X-diagonal operator. Then for any collection of positive real numbers
$T:L_1(X)\to L_1(X)$
be a bounded X-diagonal operator. Then for any collection of positive real numbers
![]() $(\varepsilon _L)_{L\in \mathcal {D}^+}$
, T is a
$(\varepsilon _L)_{L\in \mathcal {D}^+}$
, T is a
![]() $1$
-projectional factor of an operator
$1$
-projectional factor of an operator
![]() $S:L_1(X)\to L_1(X)$
with the following properties:
$S:L_1(X)\to L_1(X)$
with the following properties:
-
(a) S is X-diagonal with entries
 $(S^L)_{L\in \mathcal {D}^+}$
and
$(S^L)_{L\in \mathcal {D}^+}$
and -
(b) for every
 $L,M\in \mathcal {D}^+$
with
$L,M\in \mathcal {D}^+$
with
 $L\subset M$
, we have
$L\subset M$
, we have
 $\|S^L - S^M\| \leq \varepsilon _M$
.
$\|S^L - S^M\| \leq \varepsilon _M$
.
The above theorem is proved in two steps. The first one is to pass from an arbitrary X-diagonal operator to another one whose entries are uniformly eventually close to Haar multipliers. This is perhaps the most challenging part of the entire process. For presentation purposes, we momentarily skip this. Instead, we describe the step that follows it, which is the strong stabilisation of the entries, given the uniform eventual proximity to Haar multipliers. This is based on the Fundamental Lemma (Theorem 3.4) and a simple concentration inequality. This proof also serves as an icebreaker for the proof of the first step, which is presented later in this section.
Proposition 5.2. Let X be in
![]() $\mathcal H^{**}$
, and let
$\mathcal H^{**}$
, and let
![]() $T:L_1(X)\to L_1(X)$
be a bounded X-diagonal operator. Assume that the set of entries
$T:L_1(X)\to L_1(X)$
be a bounded X-diagonal operator. Assume that the set of entries
![]() $\{T^L:L\in \mathcal {D}^+\}$
of T is uniformly eventually close to Haar multipliers. Then for any collection of positive real numbers
$\{T^L:L\in \mathcal {D}^+\}$
of T is uniformly eventually close to Haar multipliers. Then for any collection of positive real numbers
![]() $(\varepsilon _L)_{L\in \mathcal {D}^+}$
, T is a
$(\varepsilon _L)_{L\in \mathcal {D}^+}$
, T is a
![]() $1$
-projectional factor of an X-diagonal operator
$1$
-projectional factor of an X-diagonal operator
![]() $S:L_1(X)\to L_1(X)$
so that for every
$S:L_1(X)\to L_1(X)$
so that for every
![]() $L,M\in \mathcal {D}^+$
with
$L,M\in \mathcal {D}^+$
with
![]() $L\subset M$
, we have
$L\subset M$
, we have
![]() $\|S^L - S^M\| \leq \varepsilon _M$
.
$\|S^L - S^M\| \leq \varepsilon _M$
.
We start with the probabilistic component required in the proof.
Lemma 5.3. Let
![]() $N\in \mathbb {N}$
,
$N\in \mathbb {N}$
,
![]() $M\geq 0$
,
$M\geq 0$
,
![]() $\Omega $
be a uniform probability space with
$\Omega $
be a uniform probability space with
![]() $2N$
elements, and let
$2N$
elements, and let
![]() $\Omega = \sqcup _{n=1}^N\{\omega _n^{-1},\omega _n^1\}$
be a partition of
$\Omega = \sqcup _{n=1}^N\{\omega _n^{-1},\omega _n^1\}$
be a partition of
![]() $\Omega $
into doubletons. For a function
$\Omega $
into doubletons. For a function
![]() $G:\Omega \to [-M,M]$
, define
$G:\Omega \to [-M,M]$
, define
![]() $\Phi : \{-1,1\}^N\to [-M,M]$
given by
$\Phi : \{-1,1\}^N\to [-M,M]$
given by
 $$ \begin{align} \Phi(\varepsilon) = \frac{1}{N}\sum_{n=1}^NG(\omega_n^{\varepsilon_n}). \end{align} $$
$$ \begin{align} \Phi(\varepsilon) = \frac{1}{N}\sum_{n=1}^NG(\omega_n^{\varepsilon_n}). \end{align} $$
Then
![]() $\mathbb {E}(\Phi ) = \mathbb {E}(G)$
and
$\mathbb {E}(\Phi ) = \mathbb {E}(G)$
and
![]() $\mathrm {Var}(\Phi ) \leq M^2/N$
, where on
$\mathrm {Var}(\Phi ) \leq M^2/N$
, where on
![]() $\{-1,1\}^N$
, we also consider the uniform probability measure. In particular, for any
$\{-1,1\}^N$
, we also consider the uniform probability measure. In particular, for any
![]() $\eta>0$
,
$\eta>0$
,
 $$ \begin{align} \mathbb{P}\Big(\Big| \Phi - \mathbb{E}(G)\Big| \geq \eta \Big) \leq\frac{M^2}{N\eta^2}. \end{align} $$
$$ \begin{align} \mathbb{P}\Big(\Big| \Phi - \mathbb{E}(G)\Big| \geq \eta \Big) \leq\frac{M^2}{N\eta^2}. \end{align} $$
Proof. For
![]() $1\leq n\leq N$
, let
$1\leq n\leq N$
, let
![]() $\Phi _n:\{-1,1\}^N\to [-M,M]$
given by
$\Phi _n:\{-1,1\}^N\to [-M,M]$
given by
![]() $\Phi _n(\varepsilon ) = G(\omega _n^{\varepsilon _n})$
. This is an independent sequence of random variables, and for each
$\Phi _n(\varepsilon ) = G(\omega _n^{\varepsilon _n})$
. This is an independent sequence of random variables, and for each
![]() $n\in \mathbb {N}$
, we have
$n\in \mathbb {N}$
, we have
Then
![]() $\mathbb {E}(\Phi ) = (1/N)\sum _{n=1}^N\mathbb {E}(\Phi _n) = \mathbb {E}(G)$
. By independence, we obtain
$\mathbb {E}(\Phi ) = (1/N)\sum _{n=1}^N\mathbb {E}(\Phi _n) = \mathbb {E}(G)$
. By independence, we obtain
 $$ \begin{align*} \mathrm{Var}(\Phi) = \frac{1}{N^2}\sum_{n=1}^N\mathrm{Var}(\Phi_n) \leq \frac{1}{N^2}N\frac{4M^2}{4}= \frac{M^2}{N\eta^2}. \end{align*} $$
$$ \begin{align*} \mathrm{Var}(\Phi) = \frac{1}{N^2}\sum_{n=1}^N\mathrm{Var}(\Phi_n) \leq \frac{1}{N^2}N\frac{4M^2}{4}= \frac{M^2}{N\eta^2}. \end{align*} $$
Lemma 5.4. Let K be a relatively compact subset of a Banach space. Then for every
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $\eta>0$
, there exists
$\eta>0$
, there exists
![]() $N(K,\varepsilon ,\eta )\in \mathbb {N}$
so that for every
$N(K,\varepsilon ,\eta )\in \mathbb {N}$
so that for every
![]() $N\geq N(K,\varepsilon ,\eta )$
, the following holds. For every uniform probability space
$N\geq N(K,\varepsilon ,\eta )$
, the following holds. For every uniform probability space
![]() $\Omega $
with
$\Omega $
with
![]() $2N$
elements and partition
$2N$
elements and partition
![]() $\Omega = \sqcup _{n=1}^N\{\omega _n^{-1},\omega _n^1\}$
into doubletons, for any function
$\Omega = \sqcup _{n=1}^N\{\omega _n^{-1},\omega _n^1\}$
into doubletons, for any function
![]() $G:\Omega \to K$
if we define
$G:\Omega \to K$
if we define
![]() $\Phi : \{-1,1\}^N\to \mathrm {conv}(K)$
given by
$\Phi : \{-1,1\}^N\to \mathrm {conv}(K)$
given by
 $$\begin{align*}\Phi(\varepsilon) = \frac{1}{N}\sum_{n=1}^NG(\omega_n^{\varepsilon_n})\end{align*}$$
$$\begin{align*}\Phi(\varepsilon) = \frac{1}{N}\sum_{n=1}^NG(\omega_n^{\varepsilon_n})\end{align*}$$
then
![]() $\mathbb {E}(\Phi ) = \mathbb {E}(G)$
and
$\mathbb {E}(\Phi ) = \mathbb {E}(G)$
and
Proof. The statement
![]() $\mathbb {E}(\Phi ) = \mathbb {E}(G)$
is proved exactly as in the scalar valued scenario, and it is in fact independent of the choice of
$\mathbb {E}(\Phi ) = \mathbb {E}(G)$
is proved exactly as in the scalar valued scenario, and it is in fact independent of the choice of
![]() $N(K,\varepsilon ,\eta )$
. For the second part fix
$N(K,\varepsilon ,\eta )$
. For the second part fix
![]() $\varepsilon ,\eta>0$
, and take a finite
$\varepsilon ,\eta>0$
, and take a finite
![]() $\eta /3$
-net
$\eta /3$
-net
![]() $(k_i)_{i=1}^{d(K,\eta )}$
of the set
$(k_i)_{i=1}^{d(K,\eta )}$
of the set
![]() $\mathrm {conv}(K\cup (-K))$
. Fix norm-one functionals
$\mathrm {conv}(K\cup (-K))$
. Fix norm-one functionals
![]() $(f_i)_{i=1}^{d(k,\eta )}$
so that for each
$(f_i)_{i=1}^{d(k,\eta )}$
so that for each
![]() $1\leq i\leq d(K,\eta )$
, we have
$1\leq i\leq d(K,\eta )$
, we have
![]() $f_i(k_i) = \|k_i\|$
. In particular, for any
$f_i(k_i) = \|k_i\|$
. In particular, for any
![]() $k_1,k_2\in \mathrm {co}(K)$
with
$k_1,k_2\in \mathrm {co}(K)$
with
![]() $\|k_1 - k_2\| \geq \eta $
, there exists
$\|k_1 - k_2\| \geq \eta $
, there exists
![]() $1\leq i\leq d(K,\eta )$
so that
$1\leq i\leq d(K,\eta )$
so that
![]() $|f_i(k_1) - f_i(k_2)| \geq \eta /3$
. Also set
$|f_i(k_1) - f_i(k_2)| \geq \eta /3$
. Also set
![]() $M = \sup _{k\in K}\|k\|$
.
$M = \sup _{k\in K}\|k\|$
.
We now fix N, X, G and
![]() $\Phi $
as in the statement. For
$\Phi $
as in the statement. For
![]() $1\leq i\leq d(K,\eta )$
, put
$1\leq i\leq d(K,\eta )$
, put
![]() $G_i = f_i\circ G$
and
$G_i = f_i\circ G$
and
![]() $\Phi _i = f_i\circ \Phi $
; then
$\Phi _i = f_i\circ \Phi $
; then
 $$\begin{align*}\big\{ \omega : \|\Phi(\omega) - \mathbb{E}(G)\|>\eta \big\} \subset \bigcup_{1\leq i\leq d(K,\eta)}\big\{ \omega: |\Phi_i(\omega)- \mathbb{E}(G_i) | \geq \eta/3\big\}\end{align*}$$
$$\begin{align*}\big\{ \omega : \|\Phi(\omega) - \mathbb{E}(G)\|>\eta \big\} \subset \bigcup_{1\leq i\leq d(K,\eta)}\big\{ \omega: |\Phi_i(\omega)- \mathbb{E}(G_i) | \geq \eta/3\big\}\end{align*}$$
and thus, by Lemma 5.3, we have
 $$\begin{align*}\mathbb{P}\big(\|\Phi - \mathbb{E}(G)\|>\eta\big) \leq d(K,\eta)\frac{9M^2}{N\eta^2}.\end{align*}$$
$$\begin{align*}\mathbb{P}\big(\|\Phi - \mathbb{E}(G)\|>\eta\big) \leq d(K,\eta)\frac{9M^2}{N\eta^2}.\end{align*}$$
Picking any
![]() $N(K,\varepsilon ,\eta ) \geq 9d(K,\eta )M^2/(\varepsilon \eta ^2)$
completes the proof.
$N(K,\varepsilon ,\eta ) \geq 9d(K,\eta )M^2/(\varepsilon \eta ^2)$
completes the proof.
Remark 5.5. Let X be an Haar system space,
![]() $T:L_1(X)\to L_1(X)$
be an X-diagonal operator and
$T:L_1(X)\to L_1(X)$
be an X-diagonal operator and
![]() $\Gamma $
be a disjoint collection of
$\Gamma $
be a disjoint collection of
![]() $\mathcal {D}^+$
. Then for every
$\mathcal {D}^+$
. Then for every
![]() $g\in L_\infty $
,
$g\in L_\infty $
,
![]() $f\in L_1$
, and
$f\in L_1$
, and
![]() $\theta $
in
$\theta $
in
![]() $\{-1,1\}^{\Gamma }$
, we have
$\{-1,1\}^{\Gamma }$
, we have
 $$ \begin{align*} \langle g , T^{(\nu_{\Gamma^*}h_{\Gamma}^\theta,\mu_{\Gamma^*}h_\Gamma^\theta)}f\rangle &= \langle g\otimes \nu_{\Gamma^*} h_\Gamma^\theta,T(f\otimes \mu_{\Gamma^*}h_\Gamma^\theta) \rangle\\ &=|\Gamma^*|^{-1}\sum_{M\in\Gamma}\sum_{L\in\Gamma}\theta_M\theta_L\langle g\otimes h_M,T(f\otimes h_L)\rangle\\ &= |\Gamma^*|^{-1}\sum_{M\in\Gamma}\sum_{L\in\Gamma}\theta_M\theta_L\langle g\otimes h_M,(T^Lf)\otimes h_L\rangle\\ &= |\Gamma^*|^{-1}\sum_{M\in\Gamma}\sum_{L\in\Gamma}\theta_M\theta_L\langle g,T^Lf\rangle\langle h_M,h_L\rangle\\ & = \sum_{L\in\Gamma} \big(|L|/|\Gamma^*|\big)\langle g,T^Lf\rangle. \end{align*} $$
$$ \begin{align*} \langle g , T^{(\nu_{\Gamma^*}h_{\Gamma}^\theta,\mu_{\Gamma^*}h_\Gamma^\theta)}f\rangle &= \langle g\otimes \nu_{\Gamma^*} h_\Gamma^\theta,T(f\otimes \mu_{\Gamma^*}h_\Gamma^\theta) \rangle\\ &=|\Gamma^*|^{-1}\sum_{M\in\Gamma}\sum_{L\in\Gamma}\theta_M\theta_L\langle g\otimes h_M,T(f\otimes h_L)\rangle\\ &= |\Gamma^*|^{-1}\sum_{M\in\Gamma}\sum_{L\in\Gamma}\theta_M\theta_L\langle g\otimes h_M,(T^Lf)\otimes h_L\rangle\\ &= |\Gamma^*|^{-1}\sum_{M\in\Gamma}\sum_{L\in\Gamma}\theta_M\theta_L\langle g,T^Lf\rangle\langle h_M,h_L\rangle\\ & = \sum_{L\in\Gamma} \big(|L|/|\Gamma^*|\big)\langle g,T^Lf\rangle. \end{align*} $$
In particular, the above expression does not depend on the choice of signs
![]() $\theta $
: that is, we may write
$\theta $
: that is, we may write
Proof of Proposition 5.2
Since X is in
![]() $\mathcal H^{**}$
, the conditions of the Fundamental Lemma (Theorem 3.4) are satisfied for
$\mathcal H^{**}$
, the conditions of the Fundamental Lemma (Theorem 3.4) are satisfied for
![]() $B=\{\mu _L h_L: L\in \mathcal D^+\}$
. Fix some
$B=\{\mu _L h_L: L\in \mathcal D^+\}$
. Fix some
![]() $\eta \in (0,1)$
. We apply the Fundamental Lemma to find a closed subset
$\eta \in (0,1)$
. We apply the Fundamental Lemma to find a closed subset
![]() $\mathscr {A}$
of
$\mathscr {A}$
of
![]() $[\mathcal {D}^+]$
with
$[\mathcal {D}^+]$
with
![]() $|\mathscr {A}|>1 - \eta $
and so that
$|\mathscr {A}|>1 - \eta $
and so that
![]() $\{T^{L}P_{\mathscr {A}}: L\in \mathcal D^+\}$
is relatively compact. By Proposition 2.18, there exists a subspace Z of
$\{T^{L}P_{\mathscr {A}}: L\in \mathcal D^+\}$
is relatively compact. By Proposition 2.18, there exists a subspace Z of
![]() $P_{\mathscr A}(L_1)$
that is isometrically isomorphic to
$P_{\mathscr A}(L_1)$
that is isometrically isomorphic to
![]() $L_1$
via
$L_1$
via
![]() $A:L_1\to Z$
and 1-complemented in
$A:L_1\to Z$
and 1-complemented in
![]() $L_1$
via
$L_1$
via
![]() $P:L_1\to Z$
. The operator T is a 1-projectional factor of
$P:L_1\to Z$
. The operator T is a 1-projectional factor of
![]() $S = ((A^{-1}P)\otimes I)T(A\otimes I)$
, and in fact for every
$S = ((A^{-1}P)\otimes I)T(A\otimes I)$
, and in fact for every
![]() $L\in \mathcal D^+$
, we have
$L\in \mathcal D^+$
, we have
![]() $S^{L} = A^{-1}PT^{L}A = A^{-1}PT^{L}P_{\mathscr {A}}A$
. In particular, for every set
$S^{L} = A^{-1}PT^{L}A = A^{-1}PT^{L}P_{\mathscr {A}}A$
. In particular, for every set
![]() $\{S^L:L\in \mathcal D^+\}$
is relatively compact. Let K be the closed convex hull of
$\{S^L:L\in \mathcal D^+\}$
is relatively compact. Let K be the closed convex hull of
![]() $\{S^L:L\in \mathcal D^+\}$
, with respect to the operator norm.
$\{S^L:L\in \mathcal D^+\}$
, with respect to the operator norm.
As in the proof of Theorem 4.1, for every finite disjoint collection
![]() $\Gamma $
of
$\Gamma $
of
![]() $\mathcal {D}^+$
and
$\mathcal {D}^+$
and
![]() $n\!\in \!\mathbb {N}$
, define
$n\!\in \!\mathbb {N}$
, define
![]() $\Gamma (n) = \{L\in \mathcal {D}_n: L\subset \Gamma ^*\}$
. For finitely many
$\Gamma (n) = \{L\in \mathcal {D}_n: L\subset \Gamma ^*\}$
. For finitely many
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
![]() $\Gamma (n)$
may be empty but eventually
$\Gamma (n)$
may be empty but eventually
![]() $\Gamma ^* = \Gamma (n)^*$
. Note that for n sufficiently large so that
$\Gamma ^* = \Gamma (n)^*$
. Note that for n sufficiently large so that
![]() $\Gamma ^* = \Gamma (n)^*$
, we have
$\Gamma ^* = \Gamma (n)^*$
, we have
 $$ \begin{align} S^\Gamma_{n} := S^{\Gamma(n)} = \frac{1}{\#\Gamma(n)}\sum_{L\in\Gamma(n)}S^L\in K.\end{align} $$
$$ \begin{align} S^\Gamma_{n} := S^{\Gamma(n)} = \frac{1}{\#\Gamma(n)}\sum_{L\in\Gamma(n)}S^L\in K.\end{align} $$
By the relative compactness of K, pass to an infinite subset
![]() $\mathscr {U}$
of
$\mathscr {U}$
of
![]() $\mathbb {N}$
so that for each disjoint collection
$\mathbb {N}$
so that for each disjoint collection
![]() $\Gamma $
, the limit
$\Gamma $
, the limit
![]() $S^\Gamma _\infty = \lim _{n\in \mathscr {U}}S^\Gamma _{n}$
exists. We point out for later that for any partition
$S^\Gamma _\infty = \lim _{n\in \mathscr {U}}S^\Gamma _{n}$
exists. We point out for later that for any partition
![]() $\Gamma = \Gamma _1\sqcup \cdots \sqcup \Gamma _k$
, we have
$\Gamma = \Gamma _1\sqcup \cdots \sqcup \Gamma _k$
, we have
Pick
![]() $(\delta _L)_{L\in \mathcal {D}^+}$
so that for all
$(\delta _L)_{L\in \mathcal {D}^+}$
so that for all
![]() $M\in \mathcal {D}^+$
, we have
$M\in \mathcal {D}^+$
, we have
![]() $\sum _{L\subset M}\delta _L \leq \varepsilon _M/3$
. We will recursively define a faithful Haar system
$\sum _{L\subset M}\delta _L \leq \varepsilon _M/3$
. We will recursively define a faithful Haar system
![]() $(\hat h_L)_{L\in \mathcal {D}^+}$
so that each
$(\hat h_L)_{L\in \mathcal {D}^+}$
so that each
![]() $\hat h_L = \sum _{M\in \Gamma _L}\zeta _Mh_M$
with
$\hat h_L = \sum _{M\in \Gamma _L}\zeta _Mh_M$
with
![]() $\Gamma _L\subset \mathcal {D}_{n_L}$
, with
$\Gamma _L\subset \mathcal {D}_{n_L}$
, with
![]() $n_L\in \mathscr {U}$
. We will require that additional conditions are satisfied.
$n_L\in \mathscr {U}$
. We will require that additional conditions are satisfied.
For each L, put
![]() $\Gamma _L^+ = \{M\in \mathcal {D}_{n_L+1}:M\subset [\hat h_\emptyset \hat h_L = 1]\}$
and
$\Gamma _L^+ = \{M\in \mathcal {D}_{n_L+1}:M\subset [\hat h_\emptyset \hat h_L = 1]\}$
and
![]() $\Gamma _I^- = \{M\in \mathcal {D}_{n_L+1}:M\subset [\hat h_\emptyset \hat h_L = -1]\}$
. In the case
$\Gamma _I^- = \{M\in \mathcal {D}_{n_L+1}:M\subset [\hat h_\emptyset \hat h_L = -1]\}$
. In the case
![]() $L = \emptyset $
, the set
$L = \emptyset $
, the set
![]() $\Gamma _\emptyset ^-$
is empty, and we don’t consider it, which is consistent with the fact that there is only one immediate successor of
$\Gamma _\emptyset ^-$
is empty, and we don’t consider it, which is consistent with the fact that there is only one immediate successor of
![]() $\emptyset $
in
$\emptyset $
in
![]() $\mathcal {D}^+$
. For each L, we define a disjoint collection
$\mathcal {D}^+$
. For each L, we define a disjoint collection
![]() $E_L$
of
$E_L$
of
![]() $\mathcal {D}^+$
with
$\mathcal {D}^+$
with
![]() $E_L^* = \Gamma _L^*$
. This auxiliary collection
$E_L^* = \Gamma _L^*$
. This auxiliary collection
![]() $E_L$
will be chosen in the inductive step before
$E_L$
will be chosen in the inductive step before
![]() $\Gamma _L^*$
, and in fact it will be used to choose the latter. If
$\Gamma _L^*$
, and in fact it will be used to choose the latter. If
![]() $L=\emptyset $
, put
$L=\emptyset $
, put
![]() $E_L = \{[0,1)\}$
, if
$E_L = \{[0,1)\}$
, if
![]() $L = [0,1)$
, put
$L = [0,1)$
, put
![]() $E_L = \Gamma _\emptyset $
, if
$E_L = \Gamma _\emptyset $
, if
![]() $L = L_0^+$
, put
$L = L_0^+$
, put
![]() $E_L = \Gamma _{L_0}^+$
, and if
$E_L = \Gamma _{L_0}^+$
, and if
![]() $L = L_0^-$
, put
$L = L_0^-$
, put
![]() $E_L = \Gamma _{L_0}^-$
. Below are the additional requirements for each
$E_L = \Gamma _{L_0}^-$
. Below are the additional requirements for each
![]() $L\in \mathcal {D}^+$
.
$L\in \mathcal {D}^+$
.
-
(i) The set
 $\Gamma _L$
is of the form
$\Gamma _L$
is of the form
 $E_L(n_L)$
– that is,
$E_L(n_L)$
– that is,
 $E_L$
is a disjoint collection of
$E_L$
is a disjoint collection of
 $\mathcal {D}^+$
and
$\mathcal {D}^+$
and
 $n_L$
is a sufficiently large positive integer to be chosen during the induction – and
$n_L$
is a sufficiently large positive integer to be chosen during the induction – and  $$\begin{align*}E_L(n_L) = \Big\{ M\in\mathcal{D}_{n_L}:M\subset E_L^*\Big\}.\end{align*}$$
$$\begin{align*}E_L(n_L) = \Big\{ M\in\mathcal{D}_{n_L}:M\subset E_L^*\Big\}.\end{align*}$$
-
(ii)
 $\|S^{E_L}_{n_L} - S_\infty ^{E_L}\| \leq \delta _{L}$
.
$\|S^{E_L}_{n_L} - S_\infty ^{E_L}\| \leq \delta _{L}$
. -
(iii)
 $\|S_\infty ^{E_L} - S_\infty ^{\Gamma _L^+}\| \leq \delta _L$
and
$\|S_\infty ^{E_L} - S_\infty ^{\Gamma _L^+}\| \leq \delta _L$
and
 $\|S_\infty ^{E_L} - S_\infty ^{\Gamma _L^-}\| \leq \delta _L$
.
$\|S_\infty ^{E_L} - S_\infty ^{\Gamma _L^-}\| \leq \delta _L$
.
If we have achieved this construction, we define
 $$ \begin{align*} Q&:L_1(X)\to L_1(X), \text{ by }Q(f)=\!\! \sum_{J,M\in\mathcal{D}^+}\langle h_J\otimes \nu_M\hat h_M, f \rangle |J|^{-1}h_J\!\otimes\! \mu_M\hat h_M,\\ B&:L_1(X)\to L_1(X), \text{ by } B(h_I\otimes h_L)=h_I\otimes\hat h_L.\end{align*} $$
$$ \begin{align*} Q&:L_1(X)\to L_1(X), \text{ by }Q(f)=\!\! \sum_{J,M\in\mathcal{D}^+}\langle h_J\otimes \nu_M\hat h_M, f \rangle |J|^{-1}h_J\!\otimes\! \mu_M\hat h_M,\\ B&:L_1(X)\to L_1(X), \text{ by } B(h_I\otimes h_L)=h_I\otimes\hat h_L.\end{align*} $$
Put
![]() $R = B^{-1}QSB$
. It follows that R is X-diagonal and, by Remark 5.5, for each
$R = B^{-1}QSB$
. It follows that R is X-diagonal and, by Remark 5.5, for each
![]() $L\in \mathcal {D}^+$
, we have
$L\in \mathcal {D}^+$
, we have
![]() $R^L = S^{E_L}_{n_L}$
. Then for each L, we have
$R^L = S^{E_L}_{n_L}$
. Then for each L, we have
 $$ \begin{align} \|R^L - R^{L^+}\| &= \|S^{E_L}_{n_L} - S^{E_{L^+}}_{n_{L^+}}\| \leq \|S^{\Gamma_L^+}_\infty - S^{E_{L^+}}_{n_{L^+}}\| + \|S^{E_L}_{n_L} - S^{\Gamma_L^+}_\infty\|\nonumber\\ &\leq\|S^{\Gamma_L^+}_\infty - S^{E_{L^+}}_{n_{L^+}}\| + 2\delta_L\text{ (by (ii) \& (iii))}\\ &\leq \| S^{\Gamma_L^+}_\infty - S^{E_{L^+}}_\infty\| + \|S^{E_{L^+}}_\infty - S^{E_{L^+}}_{n_{L^+}}\| + 2\delta_L\nonumber\\ &\stackrel{\text{(ii)}}{\leq} \| S^{\Gamma_L^+}_\infty - S^{E_{L^+}}_\infty\| + \delta_{L^+} + 2\delta_L = 2\delta_L + \delta_{L^+},\nonumber \end{align} $$
$$ \begin{align} \|R^L - R^{L^+}\| &= \|S^{E_L}_{n_L} - S^{E_{L^+}}_{n_{L^+}}\| \leq \|S^{\Gamma_L^+}_\infty - S^{E_{L^+}}_{n_{L^+}}\| + \|S^{E_L}_{n_L} - S^{\Gamma_L^+}_\infty\|\nonumber\\ &\leq\|S^{\Gamma_L^+}_\infty - S^{E_{L^+}}_{n_{L^+}}\| + 2\delta_L\text{ (by (ii) \& (iii))}\\ &\leq \| S^{\Gamma_L^+}_\infty - S^{E_{L^+}}_\infty\| + \|S^{E_{L^+}}_\infty - S^{E_{L^+}}_{n_{L^+}}\| + 2\delta_L\nonumber\\ &\stackrel{\text{(ii)}}{\leq} \| S^{\Gamma_L^+}_\infty - S^{E_{L^+}}_\infty\| + \delta_{L^+} + 2\delta_L = 2\delta_L + \delta_{L^+},\nonumber \end{align} $$
because, by definition,
![]() $\Gamma _L^+ = E_{L^+}$
. Similarly, we deduce
$\Gamma _L^+ = E_{L^+}$
. Similarly, we deduce
![]() $\|R^L - R^{L^-}\| \leq 2\delta _L + \delta _{L^{-}}$
. Also, using
$\|R^L - R^{L^-}\| \leq 2\delta _L + \delta _{L^{-}}$
. Also, using
![]() $S^{\Gamma _\emptyset } = S^{\Gamma _{[0,1)}}$
, we deduce
$S^{\Gamma _\emptyset } = S^{\Gamma _{[0,1)}}$
, we deduce
![]() $\|R^\emptyset - R^{[0,1)}\| \leq 2\delta _\emptyset $
. By iterating this process, we may deduce that for every
$\|R^\emptyset - R^{[0,1)}\| \leq 2\delta _\emptyset $
. By iterating this process, we may deduce that for every
![]() $L\subset M$
, we have that
$L\subset M$
, we have that
![]() $\|R^L - R^M\| \leq 3\sum _{N\subset M}\delta _N\leq \varepsilon _M$
.
$\|R^L - R^M\| \leq 3\sum _{N\subset M}\delta _N\leq \varepsilon _M$
.
It remains to explain how we ensure that conditions (i), (ii), and (iii) are upheld. We start by putting
![]() $E_\emptyset = \{[0,1)\}$
, by picking
$E_\emptyset = \{[0,1)\}$
, by picking
![]() $n_\emptyset $
sufficiently large so that
$n_\emptyset $
sufficiently large so that
![]() $\|S^{E_\emptyset }_{n_\emptyset } - S^{E_\emptyset }_\infty \| \leq \delta _\emptyset $
, and by taking
$\|S^{E_\emptyset }_{n_\emptyset } - S^{E_\emptyset }_\infty \| \leq \delta _\emptyset $
, and by taking
![]() $\zeta _M = 1$
for
$\zeta _M = 1$
for
![]() $M\in E_\emptyset ({n_\emptyset }) = \Gamma _\emptyset $
. Assume that we have carried out the construction up to a certain point and the time has come to pick
$M\in E_\emptyset ({n_\emptyset }) = \Gamma _\emptyset $
. Assume that we have carried out the construction up to a certain point and the time has come to pick
![]() $\hat h_L$
. Let
$\hat h_L$
. Let
![]() $L_0$
be the immediate predecessor of L. We will assume
$L_0$
be the immediate predecessor of L. We will assume
![]() $L = L_0^+$
. Similar arguments work if
$L = L_0^+$
. Similar arguments work if
![]() $L = L_0^-$
or if
$L = L_0^-$
or if
![]() $L = [0,1)$
. Put
$L = [0,1)$
. Put
![]() $E_L = \Gamma _{L_0}^+$
and pick
$E_L = \Gamma _{L_0}^+$
and pick
![]() $n_L\in \mathscr {U}$
so that
$n_L\in \mathscr {U}$
so that
where
![]() $N(K,1/2,\delta _L)$
is given by Lemma 5.4 to the compact set K, defined in beginning of this proof. We now apply that Lemma to
$N(K,1/2,\delta _L)$
is given by Lemma 5.4 to the compact set K, defined in beginning of this proof. We now apply that Lemma to
![]() $G:E_L(n_L+1)\to K$
with
$G:E_L(n_L+1)\to K$
with
![]() $G(M) = S^{\{M\}}_\infty $
. If we endow
$G(M) = S^{\{M\}}_\infty $
. If we endow
![]() $E_L(n_L+1)$
with the uniform probability measure, by equation (42),
$E_L(n_L+1)$
with the uniform probability measure, by equation (42),
![]() $\mathbb {E}(G) = S^{E_L(n_L+1)}_\infty $
. Because
$\mathbb {E}(G) = S^{E_L(n_L+1)}_\infty $
. Because
![]() $E_L(n_L+1)^* = E_L^*$
, we may instead write
$E_L(n_L+1)^* = E_L^*$
, we may instead write
![]() $\mathbb {E}(G) = S^{E_L}_\infty $
. We partition
$\mathbb {E}(G) = S^{E_L}_\infty $
. We partition
![]() $E_L(n_L+1)$
into doubletons by writing
$E_L(n_L+1)$
into doubletons by writing
![]() $E_L(n_L+1)= \sqcup _{M\in E_L(n_L)}\{M^+,M^{-}\}$
. For
$E_L(n_L+1)= \sqcup _{M\in E_L(n_L)}\{M^+,M^{-}\}$
. For
![]() $M\in E_L(n_L)= \Gamma _L$
define
$M\in E_L(n_L)= \Gamma _L$
define
![]() $M^1$
and
$M^1$
and
![]() $M^{-1}$
as follows.
$M^{-1}$
as follows.
 $$ \begin{align*} M^1 = \left\{ \begin{array}{ll} M^+ & \mbox{if } M\subset[\hat h_\emptyset = 1]\\ M^{-} & \mbox{if } M\subset[\hat h_\emptyset = -1] \end{array} \right.\text{ and } M^{-1} = \left\{ \begin{array}{ll} M^- & \mbox{if } M\subset[\hat h_\emptyset = 1]\\ M^{+} & \mbox{if } M\subset[\hat h_\emptyset = -1] \end{array} \right.. \end{align*} $$
$$ \begin{align*} M^1 = \left\{ \begin{array}{ll} M^+ & \mbox{if } M\subset[\hat h_\emptyset = 1]\\ M^{-} & \mbox{if } M\subset[\hat h_\emptyset = -1] \end{array} \right.\text{ and } M^{-1} = \left\{ \begin{array}{ll} M^- & \mbox{if } M\subset[\hat h_\emptyset = 1]\\ M^{+} & \mbox{if } M\subset[\hat h_\emptyset = -1] \end{array} \right.. \end{align*} $$
Take
![]() $\Phi :\{-1,1\}^{\Gamma _L}\to \mathrm {conv}(K)$
given by
$\Phi :\{-1,1\}^{\Gamma _L}\to \mathrm {conv}(K)$
given by
 $$ \begin{align*} \Phi(\zeta) = \frac{1}{\#\Gamma_L}\sum_{M\in\Gamma_L}G(M^{\zeta(M)}) = \frac{1}{\#\Gamma_L}\sum_{M\in\Gamma_L}S^{\{M^{\zeta(M)}\}}_\infty. \end{align*} $$
$$ \begin{align*} \Phi(\zeta) = \frac{1}{\#\Gamma_L}\sum_{M\in\Gamma_L}G(M^{\zeta(M)}) = \frac{1}{\#\Gamma_L}\sum_{M\in\Gamma_L}S^{\{M^{\zeta(M)}\}}_\infty. \end{align*} $$
By the choice of
![]() $n_L$
so that
$n_L$
so that
![]() $\#E_L(n_L) \geq N(K,1/2,\delta _:)$
, there exists a choice
$\#E_L(n_L) \geq N(K,1/2,\delta _:)$
, there exists a choice
![]() $\zeta \in \{-1,1\}^{\Gamma _L}$
so that
$\zeta \in \{-1,1\}^{\Gamma _L}$
so that
By equation (42) and the definition of
![]() $\Phi $
, we deduce that
$\Phi $
, we deduce that
![]() $(1/2)(\Phi (\zeta )+ \Phi (-\zeta )) = S^{E_L}_\infty $
, and therefore we also have that
$(1/2)(\Phi (\zeta )+ \Phi (-\zeta )) = S^{E_L}_\infty $
, and therefore we also have that
To finish the proof, it remains to observe that if we take
![]() $\hat h_L = \sum _{M\in \Gamma _L}\zeta (M)h_M$
, we have that
$\hat h_L = \sum _{M\in \Gamma _L}\zeta (M)h_M$
, we have that
![]() $S^{\Gamma _L^+} = \Phi (\zeta )$
and
$S^{\Gamma _L^+} = \Phi (\zeta )$
and
![]() $S^{\Gamma _L^-} = \Phi (-\zeta )$
. Indeed, taking a long and hard look at the definition of
$S^{\Gamma _L^-} = \Phi (-\zeta )$
. Indeed, taking a long and hard look at the definition of
![]() $M^1$
and
$M^1$
and
![]() $M^{-1}$
, we eventually observe that for each
$M^{-1}$
, we eventually observe that for each
![]() $M\in \Gamma _L$
, we have
$M\in \Gamma _L$
, we have
![]() $(h_\emptyset \zeta (M)h_M)|_{M^{\zeta (M)}} = 1$
and
$(h_\emptyset \zeta (M)h_M)|_{M^{\zeta (M)}} = 1$
and
![]() $(h_\emptyset \zeta (M)h_M)|_{M^{-\zeta (M)}} = -1$
. This can be seen, for example, by examining all four possible combinations of values of
$(h_\emptyset \zeta (M)h_M)|_{M^{-\zeta (M)}} = -1$
. This can be seen, for example, by examining all four possible combinations of values of
![]() $h_\emptyset |_M$
and
$h_\emptyset |_M$
and
![]() $\zeta (M)$
. Therefore, it is now evident that
$\zeta (M)$
. Therefore, it is now evident that
and therefore
![]() $S^{\Gamma _L^+}_\infty = (\#\Gamma _L)^{-1}\sum _{M\in \Gamma _L}S_\infty ^{\{M^{\zeta (M)}\}} = \Phi (\zeta )$
. Finally, by using
$S^{\Gamma _L^+}_\infty = (\#\Gamma _L)^{-1}\sum _{M\in \Gamma _L}S_\infty ^{\{M^{\zeta (M)}\}} = \Phi (\zeta )$
. Finally, by using
we see that
![]() $S_\infty ^{\Gamma _L^-} = \Phi (-\zeta )$
.
$S_\infty ^{\Gamma _L^-} = \Phi (-\zeta )$
.
Now that we are warmed up by the proof of Proposition 5.2, we are ready to proceed to the slightly more challenging proof of the following. We point out that Theorem 5.1 is an immediate consequence of Proposition 5.2 and the following Proposition 5.6.
Proposition 5.6. Let X be in
![]() $\mathcal H^{**}$
and
$\mathcal H^{**}$
and
![]() $T:L_1(X)\to L_1(X)$
be an X-diagonal operator, and let
$T:L_1(X)\to L_1(X)$
be an X-diagonal operator, and let
![]() $(\varepsilon _{(I,J)})_{(I,J)\in (\mathcal {D}^+)^2}$
be a collection of positive real numbers.Then T is a
$(\varepsilon _{(I,J)})_{(I,J)\in (\mathcal {D}^+)^2}$
be a collection of positive real numbers.Then T is a
![]() $1$
-projectional factor of an X-diagonal operator S with entries
$1$
-projectional factor of an X-diagonal operator S with entries
![]() $(S_L)_{L\in \mathcal {D}^+}$
and the property that for every
$(S_L)_{L\in \mathcal {D}^+}$
and the property that for every
![]() $L\in \mathcal {D}^+$
and
$L\in \mathcal {D}^+$
and
![]() $I\neq J\in \mathcal {D}^+$
, we have
$I\neq J\in \mathcal {D}^+$
, we have
In particular, the entries of S are uniformly eventually close to Haar multipliers.
Proof. The ‘in particular’ part follows from Lemma 4.2; we therefore focus on achieving equation (45).
For each finite disjoint collection
![]() $\Gamma $
of
$\Gamma $
of
![]() $\Delta ^+$
, we define
$\Delta ^+$
, we define
![]() $\Gamma (n)$
,
$\Gamma (n)$
,
![]() $T^\Gamma $
and
$T^\Gamma $
and
![]() $T^\Gamma _n$
as in the proof of Proposition 5.2. Because
$T^\Gamma _n$
as in the proof of Proposition 5.2. Because
![]() $X\in \mathcal {H}^{**}$
, by Theorem 3.2, applied to the set
$X\in \mathcal {H}^{**}$
, by Theorem 3.2, applied to the set
![]() $B = \{\mu _L h_L:L\in \mathcal {D}^+\}$
, for every
$B = \{\mu _L h_L:L\in \mathcal {D}^+\}$
, for every
![]() $f\in L_1$
, the set
$f\in L_1$
, the set
![]() $\{T^Lf:L\in \mathcal {D}^+\}$
is relatively compact and thus so is its convex hull. In particular, for every finite disjoint collection
$\{T^Lf:L\in \mathcal {D}^+\}$
is relatively compact and thus so is its convex hull. In particular, for every finite disjoint collection
![]() $\Gamma $
,
$\Gamma $
,
![]() $\{T^\Gamma _nf:n\in \mathbb {N}\}$
is relatively compact by equation (41). By a Cantor diagonalisation, we may find
$\{T^\Gamma _nf:n\in \mathbb {N}\}$
is relatively compact by equation (41). By a Cantor diagonalisation, we may find
![]() $\mathscr {U}\in [\mathbb {N}]^\infty $
so that
$\mathscr {U}\in [\mathbb {N}]^\infty $
so that
![]() $\mathrm {WOT}$
-
$\mathrm {WOT}$
-
![]() $\lim _{n\in \mathscr {U}}T^\Gamma _n = T^\Gamma _\infty $
exists for every finite disjoint collection
$\lim _{n\in \mathscr {U}}T^\Gamma _n = T^\Gamma _\infty $
exists for every finite disjoint collection
![]() $\Gamma $
.
$\Gamma $
.
We will define inductively two faithful Haar systems
![]() $(\widetilde h_I)_{I\in \mathcal {D}^+}$
,
$(\widetilde h_I)_{I\in \mathcal {D}^+}$
,
![]() $(\widehat h_L)_{L\in \mathcal {D}^+}$
. In each step of the induction, we will build a single vector
$(\widehat h_L)_{L\in \mathcal {D}^+}$
. In each step of the induction, we will build a single vector
![]() $\widetilde h_I$
, but we will build an entire level of vectors
$\widetilde h_I$
, but we will build an entire level of vectors
![]() $\widehat h_L$
. For example, in each of the first four steps of the inductive process, we will define, respectively, the collections of vectors
$\widehat h_L$
. For example, in each of the first four steps of the inductive process, we will define, respectively, the collections of vectors
 $$ \begin{align*} \{\widetilde h_\emptyset; \widehat h_\emptyset\},\; \{\widetilde h_{[0,1)}; \widehat h_{[0,1)}\},\; \{\widetilde h_{[0,1/2)}; \widehat h_{[0,1/2)}, \widehat h_{[1/2,1)}\}\text{ and}\\ \{\widetilde h_{[1/2,1)}; \widehat h_{[0,1/4)}, \widehat h_{[1/4,1/2)}, \widehat h_{[1/2,3/4)}, \widehat h_{[3/4,1)}\}. \end{align*} $$
$$ \begin{align*} \{\widetilde h_\emptyset; \widehat h_\emptyset\},\; \{\widetilde h_{[0,1)}; \widehat h_{[0,1)}\},\; \{\widetilde h_{[0,1/2)}; \widehat h_{[0,1/2)}, \widehat h_{[1/2,1)}\}\text{ and}\\ \{\widetilde h_{[1/2,1)}; \widehat h_{[0,1/4)}, \widehat h_{[1/4,1/2)}, \widehat h_{[1/2,3/4)}, \widehat h_{[3/4,1)}\}. \end{align*} $$
This asymmetric choice is necessary because whenever we pick a new vector
![]() $\widetilde h_I$
, we have to stabilise its interaction with all
$\widetilde h_I$
, we have to stabilise its interaction with all
![]() $\widehat h_L$
that will be defined in the future. For each
$\widehat h_L$
that will be defined in the future. For each
![]() $I,L\in \mathcal {D}^+$
, we will have
$I,L\in \mathcal {D}^+$
, we will have
![]() $\widetilde h_I = \sum _{J\in \Delta _I}h_J$
and
$\widetilde h_I = \sum _{J\in \Delta _I}h_J$
and
![]() $\widehat h_L = \sum _{M\in \Gamma _L}\zeta _M h_M$
, for some family
$\widehat h_L = \sum _{M\in \Gamma _L}\zeta _M h_M$
, for some family
![]() $(\zeta _M:M\in \Gamma _L)\subset \{\pm 1\}$
.
$(\zeta _M:M\in \Gamma _L)\subset \{\pm 1\}$
.
Let us set up the stage that will allow us to state the somewhat lengthy inductive hypothesis. For each
![]() $I\in \mathcal {D}^+$
, let
$I\in \mathcal {D}^+$
, let
 $$\begin{align*}\varepsilon_I' = \min_{\big\{\substack{J,J'\in\mathcal{D}^+:\\\iota(J),\iota(J')\leq\iota(I)}\big\}}\varepsilon_{(J,J')}\end{align*}$$
$$\begin{align*}\varepsilon_I' = \min_{\big\{\substack{J,J'\in\mathcal{D}^+:\\\iota(J),\iota(J')\leq\iota(I)}\big\}}\varepsilon_{(J,J')}\end{align*}$$
and fix
![]() $(\delta _L)_{L\in \mathcal {D}^+}$
so that for all
$(\delta _L)_{L\in \mathcal {D}^+}$
so that for all
![]() $M\in \mathcal {D}^+$
, we have
$M\in \mathcal {D}^+$
, we have
Here,
![]() $\mathcal {D}_{-1} = \{\emptyset \}$
and
$\mathcal {D}_{-1} = \{\emptyset \}$
and
![]() $\mathcal {D}_0 = \{[0,1)\}$
. For each
$\mathcal {D}_0 = \{[0,1)\}$
. For each
![]() $k\in \mathbb {N}$
, and for every
$k\in \mathbb {N}$
, and for every
![]() $L\in \mathcal {D}_{k-2}$
, we have for some
$L\in \mathcal {D}_{k-2}$
, we have for some
![]() $n_L\in \mathscr {U}$
,
$n_L\in \mathscr {U}$
,
![]() $\Gamma _L$
is a finite disjoint collection of
$\Gamma _L$
is a finite disjoint collection of
![]() $\mathcal {D}_{n_L}$
and
$\mathcal {D}_{n_L}$
and
![]() $|\Gamma _L^*| = |L|$
. Additionally, if
$|\Gamma _L^*| = |L|$
. Additionally, if
![]() $\iota (I) = k$
, the following hold:
$\iota (I) = k$
, the following hold:
-
(a) For some
 $\alpha _k\in \mathbb {N}$
,
$\alpha _k\in \mathbb {N}$
,
 $\Delta _I$
is a disjoint collection of
$\Delta _I$
is a disjoint collection of
 $\mathcal {D}^{\alpha _k}\setminus \mathcal {D}^{\alpha _{k-1}}$
and
$\mathcal {D}^{\alpha _k}\setminus \mathcal {D}^{\alpha _{k-1}}$
and
 $|\Delta _I| = |I|$
. If
$|\Delta _I| = |I|$
. If
 $k>1$
, then
$k>1$
, then
 $\alpha _k>a_{k-1}$
, and we put
$\alpha _k>a_{k-1}$
, and we put
 $\mathcal {D}^{\alpha _0} = \emptyset $
.
$\mathcal {D}^{\alpha _0} = \emptyset $
. -
(b) For every
 $J\in \mathcal {D}^+$
with
$J\in \mathcal {D}^+$
with
 $\iota (J)<k$
and every
$\iota (J)<k$
and every
 $M\in \mathcal {D}^{k-2}$
, we have
$M\in \mathcal {D}^{k-2}$
, we have  $$\begin{align*}\big|\big\langle \widetilde h_I, T^{\Gamma_M}\big(|J|^{-1}\widetilde h_J\big)\big\rangle\big| \leq \varepsilon_I'/2\text{ and }\big|\big\langle \widetilde h_J, T^{\Gamma_M}\big(|I|^{-1}\widetilde h_I\big)\big\rangle\big| \leq \varepsilon_I'/2.\end{align*}$$
$$\begin{align*}\big|\big\langle \widetilde h_I, T^{\Gamma_M}\big(|J|^{-1}\widetilde h_J\big)\big\rangle\big| \leq \varepsilon_I'/2\text{ and }\big|\big\langle \widetilde h_J, T^{\Gamma_M}\big(|I|^{-1}\widetilde h_I\big)\big\rangle\big| \leq \varepsilon_I'/2.\end{align*}$$
We will impose additional conditions. As in the proof of Proposition 5.2, we put
![]() $\Gamma _L^+ = \{M\in \mathcal {D}_{n_L+1}:M\subset [\tilde h_\emptyset \tilde h_L = 1]\}$
and
$\Gamma _L^+ = \{M\in \mathcal {D}_{n_L+1}:M\subset [\tilde h_\emptyset \tilde h_L = 1]\}$
and
![]() $\Gamma _L^- = \{M\in \mathcal {D}_{n_L+1}:M\subset [\tilde h_\emptyset \tilde h_L = -1]\}$
, for each L. If
$\Gamma _L^- = \{M\in \mathcal {D}_{n_L+1}:M\subset [\tilde h_\emptyset \tilde h_L = -1]\}$
, for each L. If
![]() $L=\emptyset $
, put
$L=\emptyset $
, put
![]() $E_L = \{[0,1)\}$
, if
$E_L = \{[0,1)\}$
, if
![]() $L = [0,1)$
, put
$L = [0,1)$
, put
![]() $E_L = \Gamma _\emptyset $
, if
$E_L = \Gamma _\emptyset $
, if
![]() $L = L_0^+$
, put
$L = L_0^+$
, put
![]() $E_L = \Gamma _{L_0}^+$
, and if
$E_L = \Gamma _{L_0}^+$
, and if
![]() $L = L_0^-$
, put
$L = L_0^-$
, put
![]() $E_L = \Gamma _{L_0}^-$
. Furthermore, for each
$E_L = \Gamma _{L_0}^-$
. Furthermore, for each
![]() $\alpha \in \mathbb {N}$
let
$\alpha \in \mathbb {N}$
let
![]() $P_\alpha :L_1\to L_1$
, denote the canonical projection onto
$P_\alpha :L_1\to L_1$
, denote the canonical projection onto
![]() $\langle \{h_I:I\in \mathcal {D}^\alpha \}\rangle $
. We require the following for each
$\langle \{h_I:I\in \mathcal {D}^\alpha \}\rangle $
. We require the following for each
![]() $L\in \mathcal {D}_{k-2}$
:
$L\in \mathcal {D}_{k-2}$
:
-
(i) The set
 $\Gamma _L$
is of the form
$\Gamma _L$
is of the form
 $E_L(n_L)$
.
$E_L(n_L)$
. -
(ii)
 $\|P_{\alpha _k}(T^{E_L}_{n_L} - T_\infty ^{E_L})P_{\alpha _k}\| \leq \delta _{L}$
.
$\|P_{\alpha _k}(T^{E_L}_{n_L} - T_\infty ^{E_L})P_{\alpha _k}\| \leq \delta _{L}$
. -
(iii)
 $\|P_{\alpha _k}(T_\infty ^{E_L} - T_\infty ^{\Gamma _L^+})P_{\alpha _k}\| \leq \delta _L$
and
$\|P_{\alpha _k}(T_\infty ^{E_L} - T_\infty ^{\Gamma _L^+})P_{\alpha _k}\| \leq \delta _L$
and
 $\|P_{\alpha _k}(T_\infty ^{E_L} - T_\infty ^{\Gamma _L^-})P_{\alpha _k}\| \leq \delta _L$
.
$\|P_{\alpha _k}(T_\infty ^{E_L} - T_\infty ^{\Gamma _L^-})P_{\alpha _k}\| \leq \delta _L$
.
One might jump to the conclusion that the weaker property that for each
![]() $k\in \mathbb {N}$
,
$k\in \mathbb {N}$
,
![]() $\lim _{n\in \mathscr {U}} P_kT_n^\Gamma P_k$
exists is sufficient to yield the same result. This is in fact false. We would not know that
$\lim _{n\in \mathscr {U}} P_kT_n^\Gamma P_k$
exists is sufficient to yield the same result. This is in fact false. We would not know that
![]() $T^\Gamma _\infty :L_1\to L_1$
is well defined as the Haar system is not boundedly complete. In the inductive step, the operators
$T^\Gamma _\infty :L_1\to L_1$
is well defined as the Haar system is not boundedly complete. In the inductive step, the operators
![]() $T^{E_L}_\infty $
,
$T^{E_L}_\infty $
,
![]() $L\in \mathcal {D}_{k-2}$
are used in the choice of
$L\in \mathcal {D}_{k-2}$
are used in the choice of
![]() $\widetilde h_I$
,
$\widetilde h_I$
,
![]() $\iota (I) = k$
. Therefore the fact that for each
$\iota (I) = k$
. Therefore the fact that for each
![]() $\Gamma $
,
$\Gamma $
,
![]() $\mathrm {WOT}$
-
$\mathrm {WOT}$
-
![]() $\lim _{n\in \mathscr {U}}T^{\Gamma }_n = T^\Gamma _\infty $
is necessary.
$\lim _{n\in \mathscr {U}}T^{\Gamma }_n = T^\Gamma _\infty $
is necessary.
We assume that we have completed the construction to finish the proof. Take the isometry A given by
![]() $A(h_I\otimes h_L) = \widetilde h_I\otimes \widehat h_L$
and the norm-one projection P onto the image of A given by
$A(h_I\otimes h_L) = \widetilde h_I\otimes \widehat h_L$
and the norm-one projection P onto the image of A given by
 $$\begin{align*}P(u)= \sum_{I,L\in\mathcal{D}^+}\big\langle\widetilde h_I\otimes |L|^{-1/q}\widehat h_L, u \big\rangle |I|^{-1}\widetilde h_I\otimes|L|^{-1/p}\widehat h_L.\end{align*}$$
$$\begin{align*}P(u)= \sum_{I,L\in\mathcal{D}^+}\big\langle\widetilde h_I\otimes |L|^{-1/q}\widehat h_L, u \big\rangle |I|^{-1}\widetilde h_I\otimes|L|^{-1/p}\widehat h_L.\end{align*}$$
The operator T is a 1-projectional factor of
![]() $S = A^{-1}PTA$
, and S is X-diagonal with entries
$S = A^{-1}PTA$
, and S is X-diagonal with entries
![]() $(S^L)_{L\in \mathcal {D}^+}$
so that for each
$(S^L)_{L\in \mathcal {D}^+}$
so that for each
![]() $L,I,J\in \mathcal {D}^+$
, we have
$L,I,J\in \mathcal {D}^+$
, we have
We fix
![]() $I\neq J\in \mathcal {D}^+$
with
$I\neq J\in \mathcal {D}^+$
with
![]() $\iota (J)<\iota (I) = k$
and
$\iota (J)<\iota (I) = k$
and
![]() $L\in \mathcal {D}^+$
. If
$L\in \mathcal {D}^+$
. If
![]() $L\in \mathcal {D}^{k-2}$
, then by (b), we have
$L\in \mathcal {D}^{k-2}$
, then by (b), we have
 $$ \begin{align} \begin{split} \big|\big\langle h_I, S^L\big(|J|^{-1} h_J\big)\big\rangle\big| &\leq \varepsilon_I'/2\leq \varepsilon_{(I,J)}\text{ and }\\ \big|\big\langle h_J, S^L\big(|I|^{-1} h_I\big)\big\rangle\big| &\leq \varepsilon_I'/2\leq \varepsilon_{(J,I)}. \end{split} \end{align} $$
$$ \begin{align} \begin{split} \big|\big\langle h_I, S^L\big(|J|^{-1} h_J\big)\big\rangle\big| &\leq \varepsilon_I'/2\leq \varepsilon_{(I,J)}\text{ and }\\ \big|\big\langle h_J, S^L\big(|I|^{-1} h_I\big)\big\rangle\big| &\leq \varepsilon_I'/2\leq \varepsilon_{(J,I)}. \end{split} \end{align} $$
Assume then that
![]() $L\in \mathcal {D}_{k'-2}$
with
$L\in \mathcal {D}_{k'-2}$
with
![]() $k'> k$
. Let
$k'> k$
. Let
![]() $L_k,\ldots ,L_{k'-1},L_{k'} = L$
be a sequence with
$L_k,\ldots ,L_{k'-1},L_{k'} = L$
be a sequence with
![]() $L_j\in \mathcal {D}^+_{j-2}$
and each term a direct successor of the one before it. Repeat the argument from equation (43) to deduce that for
$L_j\in \mathcal {D}^+_{j-2}$
and each term a direct successor of the one before it. Repeat the argument from equation (43) to deduce that for
![]() $k\leq j<k'$
,
$k\leq j<k'$
,
 $$ \begin{align*} \big\|P_{\alpha_k}(T^{\Gamma_{L_j}} - T^{\Gamma_{L_{j+1}}})P_{\alpha_k}\big\| \leq \big\|P_{\alpha_j}(T^{\Gamma_{L_j}} - T^{\Gamma_{L_{j+1}}})P_{\alpha_j}\big\| \leq 2\delta_{L_j} + \delta_{L_{j+1}}\text{: that is,}\\ \big\|P_{\alpha_k}(T^{\Gamma_L} - T^{\Gamma_{L_{k}}})P_{\alpha_k}\big\| \leq 3\sum_{M\subset L_k}\delta_M \leq \varepsilon_{L_k}'/2\leq \varepsilon_{I}'/2 \text{ (because }\iota(I)\leq\iota(L_k)\text{).} \end{align*} $$
$$ \begin{align*} \big\|P_{\alpha_k}(T^{\Gamma_{L_j}} - T^{\Gamma_{L_{j+1}}})P_{\alpha_k}\big\| \leq \big\|P_{\alpha_j}(T^{\Gamma_{L_j}} - T^{\Gamma_{L_{j+1}}})P_{\alpha_j}\big\| \leq 2\delta_{L_j} + \delta_{L_{j+1}}\text{: that is,}\\ \big\|P_{\alpha_k}(T^{\Gamma_L} - T^{\Gamma_{L_{k}}})P_{\alpha_k}\big\| \leq 3\sum_{M\subset L_k}\delta_M \leq \varepsilon_{L_k}'/2\leq \varepsilon_{I}'/2 \text{ (because }\iota(I)\leq\iota(L_k)\text{).} \end{align*} $$
Therefore,
 $$ \begin{align*} \big|\big\langle h_I, S^L\big(|J|^{-1} h_J\big)\big\rangle\big| &= \big|\big\langle \widetilde h_I, T^{\Gamma_L}\big(|J|^{-1}\widetilde h_J\big)\big\rangle\big| = \big|\big\langle \widetilde h_I, P_{\alpha_k}T^{\Gamma_L}P_{\alpha_k}\big(|J|^{-1}\widetilde h_J\big)\big\rangle\big|\\ & \leq \big|\big\langle \widetilde h_I, P_{\alpha_k}T^{\Gamma_{L_k}}P_{\alpha_k}\big(|J|^{-1}\widetilde h_J\big)\big\rangle\big| + \varepsilon^{\prime}_I/2\\ & = \big|\big\langle \widetilde h_I, T^{\Gamma_{L_k}}\big(|J|^{-1}\widetilde h_J\big)\big\rangle\big| + \varepsilon^{\prime}_I/2\\ & = \big|\big\langle h_I, S^{L_k}\big(|J|^{-1} h_J\big)\big\rangle\big| + \varepsilon^{\prime}_I/2 \stackrel{equation(46)}{\leq} \varepsilon^{\prime}_I/2+\varepsilon^{\prime}_I/2 \leq \varepsilon_{(I,J)}. \end{align*} $$
$$ \begin{align*} \big|\big\langle h_I, S^L\big(|J|^{-1} h_J\big)\big\rangle\big| &= \big|\big\langle \widetilde h_I, T^{\Gamma_L}\big(|J|^{-1}\widetilde h_J\big)\big\rangle\big| = \big|\big\langle \widetilde h_I, P_{\alpha_k}T^{\Gamma_L}P_{\alpha_k}\big(|J|^{-1}\widetilde h_J\big)\big\rangle\big|\\ & \leq \big|\big\langle \widetilde h_I, P_{\alpha_k}T^{\Gamma_{L_k}}P_{\alpha_k}\big(|J|^{-1}\widetilde h_J\big)\big\rangle\big| + \varepsilon^{\prime}_I/2\\ & = \big|\big\langle \widetilde h_I, T^{\Gamma_{L_k}}\big(|J|^{-1}\widetilde h_J\big)\big\rangle\big| + \varepsilon^{\prime}_I/2\\ & = \big|\big\langle h_I, S^{L_k}\big(|J|^{-1} h_J\big)\big\rangle\big| + \varepsilon^{\prime}_I/2 \stackrel{equation(46)}{\leq} \varepsilon^{\prime}_I/2+\varepsilon^{\prime}_I/2 \leq \varepsilon_{(I,J)}. \end{align*} $$
Repeating the argument yields
![]() $|\langle h_J, S^L(|I|^{-1} h_I)\rangle | \leq \varepsilon _{(J,I)}$
. To complete the proof, we still need to carry out the inductive construction. In the first step, we may take
$|\langle h_J, S^L(|I|^{-1} h_I)\rangle | \leq \varepsilon _{(J,I)}$
. To complete the proof, we still need to carry out the inductive construction. In the first step, we may take
![]() $\widetilde h_\emptyset = h_\emptyset $
(i.e.,
$\widetilde h_\emptyset = h_\emptyset $
(i.e.,
![]() $\Delta _\emptyset = \{\emptyset \}$
), and thus we may take, for example,
$\Delta _\emptyset = \{\emptyset \}$
), and thus we may take, for example,
![]() $\alpha _1 = 1$
. Next, we pick
$\alpha _1 = 1$
. Next, we pick
![]() $n_\emptyset \in \mathscr {U}$
sufficiently large so that we have
$n_\emptyset \in \mathscr {U}$
sufficiently large so that we have
![]() $\|P_1(T^{\{[0,1)\}}_{n_\emptyset } - T^{\{[0,1)\}}_\infty )P_1\|\ \leq \delta _\emptyset $
. We put
$\|P_1(T^{\{[0,1)\}}_{n_\emptyset } - T^{\{[0,1)\}}_\infty )P_1\|\ \leq \delta _\emptyset $
. We put
![]() $\widehat h_\emptyset = \sum _{M\in E_\emptyset (n_\emptyset )} h_L$
(i.e.,
$\widehat h_\emptyset = \sum _{M\in E_\emptyset (n_\emptyset )} h_L$
(i.e.,
![]() $\Gamma _\emptyset = E_\emptyset (n_\emptyset )$
with
$\Gamma _\emptyset = E_\emptyset (n_\emptyset )$
with
![]() $E_\emptyset = \{[0,1)\}$
and
$E_\emptyset = \{[0,1)\}$
and
![]() $\zeta _M = 1$
for
$\zeta _M = 1$
for
![]() $M\in \Gamma _\emptyset $
). The only nontrivial condition to check is (iii), which follows from the fact that
$M\in \Gamma _\emptyset $
). The only nontrivial condition to check is (iii), which follows from the fact that
![]() $E_\emptyset ^* = (\Gamma _\emptyset ^+)^*$
and thus
$E_\emptyset ^* = (\Gamma _\emptyset ^+)^*$
and thus
![]() $T^{E_\emptyset }_\infty = T^{\Gamma ^+_\emptyset }_\infty $
. We do not consider the set
$T^{E_\emptyset }_\infty = T^{\Gamma ^+_\emptyset }_\infty $
. We do not consider the set
![]() $\Gamma _\emptyset ^-$
.
$\Gamma _\emptyset ^-$
.
We now present the kth step for
![]() $k\geq 2$
. Let
$k\geq 2$
. Let
![]() $I\in \mathcal {D}^+$
with
$I\in \mathcal {D}^+$
with
![]() $\iota (I) = k$
, and denote by
$\iota (I) = k$
, and denote by
![]() $I_0$
its immediate predecessor. We will assume that
$I_0$
its immediate predecessor. We will assume that
![]() $I = I_0^+$
. For each
$I = I_0^+$
. For each
![]() $L\in \mathcal {D}_{k-2}$
, we denote its immediate predecessor by
$L\in \mathcal {D}_{k-2}$
, we denote its immediate predecessor by
![]() $L_0$
. Recall that for each such L, the set
$L_0$
. Recall that for each such L, the set
![]() $E_L$
has been defined based on whether
$E_L$
has been defined based on whether
![]() $L = L_0^+$
or
$L = L_0^+$
or
![]() $L = L_0^-$
. Consider the following finite sets:
$L = L_0^-$
. Consider the following finite sets:
 $$ \begin{align*} \mathscr{T} &= \big\{T^{\Gamma_L}:L\in\mathcal{D}^{k-3}\big\}\cup\big\{T^{E_L}_\infty:L\in\mathcal{D}_{k-2}\big\}\subset\mathcal{L}(L_1),\\ G&=\big\{\widetilde h_J:\iota(K)<k\big\}\subset L_\infty\text{ and }F = \big\{|J|^{-1}\widetilde h_J:\iota(J)<k\big\}. \end{align*} $$
$$ \begin{align*} \mathscr{T} &= \big\{T^{\Gamma_L}:L\in\mathcal{D}^{k-3}\big\}\cup\big\{T^{E_L}_\infty:L\in\mathcal{D}_{k-2}\big\}\subset\mathcal{L}(L_1),\\ G&=\big\{\widetilde h_J:\iota(K)<k\big\}\subset L_\infty\text{ and }F = \big\{|J|^{-1}\widetilde h_J:\iota(J)<k\big\}. \end{align*} $$
By Lemma 4.3, there exists
![]() $i_0\in \mathbb {N}$
so that for any finite disjoint collection
$i_0\in \mathbb {N}$
so that for any finite disjoint collection
![]() $\Delta \subset \mathcal {D}^+$
with
$\Delta \subset \mathcal {D}^+$
with
![]() $\min \iota (\Delta ) \geq i_0$
and any
$\min \iota (\Delta ) \geq i_0$
and any
![]() $\theta \in \{-1,1\}^\Delta $
, we have that for all
$\theta \in \{-1,1\}^\Delta $
, we have that for all
![]() $T\in \mathscr {T}$
,
$T\in \mathscr {T}$
,
![]() $g\in G$
and
$g\in G$
and
![]() $f\in F$
$f\in F$
We pick
![]() $\Delta _I$
with
$\Delta _I$
with
![]() $\min \iota (\Delta _I)\geq i_0$
and so that (b) is satisfied. The integer
$\min \iota (\Delta _I)\geq i_0$
and so that (b) is satisfied. The integer
![]() $\alpha _k$
is simply chosen so that
$\alpha _k$
is simply chosen so that
![]() $P_{\alpha _k}\widetilde h_I = \widetilde h_I$
. It is immediate that condition (b) is satisfied for all
$P_{\alpha _k}\widetilde h_I = \widetilde h_I$
. It is immediate that condition (b) is satisfied for all
![]() $M\in \mathcal {D}^{k-3}$
. Later we will show that (b) also holds for
$M\in \mathcal {D}^{k-3}$
. Later we will show that (b) also holds for
![]() $M\in \mathcal {D}^{k-2}$
.
$M\in \mathcal {D}^{k-2}$
.
In the next step, for each
![]() $L\in \mathcal {D}_{k-2}$
, we need to pick
$L\in \mathcal {D}_{k-2}$
, we need to pick
![]() $n_L$
that defined
$n_L$
that defined
![]() $\Gamma _L$
and
$\Gamma _L$
and
![]() $\zeta _L\in \{-1,1\}^{\Gamma _L}$
. The choice of
$\zeta _L\in \{-1,1\}^{\Gamma _L}$
. The choice of
![]() $n_L$
so that (i) and (ii) are satisfied is easy. However, we wish to ensure that we can additionally achieve condition (iii), and for this we need Lemma 5.4. Consider the relatively compact set
$n_L$
so that (i) and (ii) are satisfied is easy. However, we wish to ensure that we can additionally achieve condition (iii), and for this we need Lemma 5.4. Consider the relatively compact set
![]() $K = \{P_{\alpha _k}T_\infty ^{\Gamma }P_{\alpha _k}: \Gamma $
is a finite disjoint collection of
$K = \{P_{\alpha _k}T_\infty ^{\Gamma }P_{\alpha _k}: \Gamma $
is a finite disjoint collection of
![]() $\mathcal {D}^+\}\subset \mathcal {L}(L_1)$
, and take
$\mathcal {D}^+\}\subset \mathcal {L}(L_1)$
, and take
![]() $N(K,2^{-k},\varepsilon _I'/6)$
given by Lemma 5.4. For each
$N(K,2^{-k},\varepsilon _I'/6)$
given by Lemma 5.4. For each
![]() $L\in \mathcal {D}^{k-2}$
, pick
$L\in \mathcal {D}^{k-2}$
, pick
![]() $n_L\in \mathscr {U}$
so that (ii) is satisfied as well as
$n_L\in \mathscr {U}$
so that (ii) is satisfied as well as
![]() $\#E_L(n_L) \geq N(K,2^{-k},\varepsilon _I'/6)$
. The objective is to pick, for each
$\#E_L(n_L) \geq N(K,2^{-k},\varepsilon _I'/6)$
. The objective is to pick, for each
![]() $L\in \mathcal {D}_{k-2}$
, signs
$L\in \mathcal {D}_{k-2}$
, signs
![]() $\zeta _L\in \{-1,1\}^{\Gamma _L}$
so that (iii) is satisfied. Repeating, word for word, the argument from the last few paragraphs of the proof of Proposition 5.2, we can do exactly that.
$\zeta _L\in \{-1,1\}^{\Gamma _L}$
so that (iii) is satisfied. Repeating, word for word, the argument from the last few paragraphs of the proof of Proposition 5.2, we can do exactly that.
The final touch that is required to complete the proof is to observe that (b) is now also satisfied for all
![]() $L\in \mathcal {D}_{k-2}$
. Indeed, for
$L\in \mathcal {D}_{k-2}$
. Indeed, for
![]() $J\in \mathcal {D}^+$
with
$J\in \mathcal {D}^+$
with
![]() $\iota (J) < k$
, we have
$\iota (J) < k$
, we have
 $$ \begin{align*} \big|\big\langle \widetilde h_I, T^{\Gamma_L}\big(|J|^{-1}\widetilde h_J\big)\big\rangle\big| &= \big|\big\langle P_{\alpha_k}^*\widetilde h_I, T^{E_L}_{n_L}P_{\alpha_k}\big(|J|^{-1}\widetilde h_J\big)\big\rangle\big|\\ &= \big|\big\langle\widetilde h_I, P_{\alpha_k}T^{E_L}_{n_L} P_{\alpha_k}\big(|J|^{-1}\widetilde h_J\big)\big\rangle\big|\\ & \stackrel{\text{(ii)}}{\leq} \big|\big\langle\widetilde h_I, P_{\alpha_k}T^{E_L}_\infty P_{\alpha_k}\big(|J|^{-1}\widetilde h_J\big)\big\rangle\big| + \delta_L\\ & \stackrel{\text{equation(47)}}{\leq} \varepsilon_I'/3 + \delta_L \leq \varepsilon_I'/3 + \varepsilon_I'/6 = \varepsilon_I'/2. \end{align*} $$
$$ \begin{align*} \big|\big\langle \widetilde h_I, T^{\Gamma_L}\big(|J|^{-1}\widetilde h_J\big)\big\rangle\big| &= \big|\big\langle P_{\alpha_k}^*\widetilde h_I, T^{E_L}_{n_L}P_{\alpha_k}\big(|J|^{-1}\widetilde h_J\big)\big\rangle\big|\\ &= \big|\big\langle\widetilde h_I, P_{\alpha_k}T^{E_L}_{n_L} P_{\alpha_k}\big(|J|^{-1}\widetilde h_J\big)\big\rangle\big|\\ & \stackrel{\text{(ii)}}{\leq} \big|\big\langle\widetilde h_I, P_{\alpha_k}T^{E_L}_\infty P_{\alpha_k}\big(|J|^{-1}\widetilde h_J\big)\big\rangle\big| + \delta_L\\ & \stackrel{\text{equation(47)}}{\leq} \varepsilon_I'/3 + \delta_L \leq \varepsilon_I'/3 + \varepsilon_I'/6 = \varepsilon_I'/2. \end{align*} $$
The same argument yields
![]() $|\langle \widetilde h_J,T^{\Gamma _L}(|I|^{-1}\widetilde h_I)\rangle | \leq \varepsilon _I'/2$
.
$|\langle \widetilde h_J,T^{\Gamma _L}(|I|^{-1}\widetilde h_I)\rangle | \leq \varepsilon _I'/2$
.
6 Projectional factors of scalar operators
In this section, we provide the finishing touches to prove our main result.
Theorem 6.1. Let X be in
![]() $\mathcal H^*$
and
$\mathcal H^*$
and
![]() $\mathcal H^{**}$
, and let
$\mathcal H^{**}$
, and let
![]() $T:L_1(X)\to L_1(X)$
be a bounded linear operator. Then for every
$T:L_1(X)\to L_1(X)$
be a bounded linear operator. Then for every
![]() $\varepsilon>0$
, T is a 1-projectional factor with error
$\varepsilon>0$
, T is a 1-projectional factor with error
![]() $\varepsilon $
of a scalar operator. In particular,
$\varepsilon $
of a scalar operator. In particular,
![]() $L_1(X)$
is primary.
$L_1(X)$
is primary.
We first need to prove a perturbation result that will allow us to pass from Theorem 5.1 to the conclusion.
Proposition 6.2. Let X be a Haar system space and
![]() $T:L_1(X)\to L_1(X)$
be an X-diagonal operator with entries
$T:L_1(X)\to L_1(X)$
be an X-diagonal operator with entries
![]() $(T^L)_{L\in \mathcal {D}^+}$
, and let
$(T^L)_{L\in \mathcal {D}^+}$
, and let
![]() $\varepsilon>0$
. Assume that for all
$\varepsilon>0$
. Assume that for all
![]() $L,M\in \mathcal {D}^+$
with
$L,M\in \mathcal {D}^+$
with
![]() $L\subset M$
, we have
$L\subset M$
, we have
![]() $\|T^L - T^M\| \leq \varepsilon |M|^2$
. Then
$\|T^L - T^M\| \leq \varepsilon |M|^2$
. Then
![]() $\|T - T^\emptyset \otimes I\| \leq 7\varepsilon $
.
$\|T - T^\emptyset \otimes I\| \leq 7\varepsilon $
.
Remark 6.3. Let
![]() $n_0\in \mathbb {N}$
, and for each
$n_0\in \mathbb {N}$
, and for each
![]() $L\in \mathcal {D}_{n_0}$
, let
$L\in \mathcal {D}_{n_0}$
, let
![]() $(\theta _k^{L})_{k=0}^{n_0}$
be the signs given by equation (20). Then for scalars
$(\theta _k^{L})_{k=0}^{n_0}$
be the signs given by equation (20). Then for scalars
![]() $(a_L)_{L\in \mathcal {D}_{n_0}}$
, we may write
$(a_L)_{L\in \mathcal {D}_{n_0}}$
, we may write
 $$\begin{align*}\sum_{L\in\mathcal{D}_{n_0}}a_L|L|^{-1}\chi_L = \big(\!\!\!\sum_{L\in\mathcal{D}_{n_0}}\!\!\!a_L\big)h_\emptyset + \sum_{k=1}^{n_0}\sum_{M\in\mathcal{D}_{k-1}}\Big(\!\!\!\!\sum_{\big\{\substack{L\in\mathcal{D}_{n_0}:\\ L\subset M}\big\}}\!\!\!\!\theta_k^La_L\Big)|M|^{-1}h_M.\end{align*}$$
$$\begin{align*}\sum_{L\in\mathcal{D}_{n_0}}a_L|L|^{-1}\chi_L = \big(\!\!\!\sum_{L\in\mathcal{D}_{n_0}}\!\!\!a_L\big)h_\emptyset + \sum_{k=1}^{n_0}\sum_{M\in\mathcal{D}_{k-1}}\Big(\!\!\!\!\sum_{\big\{\substack{L\in\mathcal{D}_{n_0}:\\ L\subset M}\big\}}\!\!\!\!\theta_k^La_L\Big)|M|^{-1}h_M.\end{align*}$$
We now take an RI space X and translate this into the X setting. For
![]() $k=0,\ldots ,n_0$
, put
$k=0,\ldots ,n_0$
, put
![]() $\mu _k = \mu _L$
and
$\mu _k = \mu _L$
and
![]() $\nu _k = \nu _L$
for
$\nu _k = \nu _L$
for
![]() $L\in \mathcal {D}_k$
. Multiply both sides by
$L\in \mathcal {D}_k$
. Multiply both sides by
![]() $\nu _{n_0}^{-1}$
so that for
$\nu _{n_0}^{-1}$
so that for
![]() $L\in \mathcal {D}_{n_0}$
, we have
$L\in \mathcal {D}_{n_0}$
, we have
![]() $|L|^{-1}\nu _{n_0}^{-1} = \mu _L$
.
$|L|^{-1}\nu _{n_0}^{-1} = \mu _L$
.
 $$ \begin{align} \sum_{L\in\mathcal{D}_{n_0}}a_L\mu_L\chi_L = \nu_{n_0}^{-1}\big(\!\!\!\sum_{L\in\mathcal{D}_{n_0}}\!\!\!a_L\big)h_\emptyset + \nu_{n_0}^{-1}\sum_{k=1}^{n_0}\nu_{k-1}\!\!\!\!\sum_{M\in\mathcal{D}_{k-1}} \Big(\!\!\!\!\sum_{\big\{\substack{L\in\mathcal{D}_{n_0}:\\ L\subset M}\big\}}\!\!\!\!\theta_k^La_L\Big)\mu_Mh_M.\nonumber \end{align} $$
$$ \begin{align} \sum_{L\in\mathcal{D}_{n_0}}a_L\mu_L\chi_L = \nu_{n_0}^{-1}\big(\!\!\!\sum_{L\in\mathcal{D}_{n_0}}\!\!\!a_L\big)h_\emptyset + \nu_{n_0}^{-1}\sum_{k=1}^{n_0}\nu_{k-1}\!\!\!\!\sum_{M\in\mathcal{D}_{k-1}} \Big(\!\!\!\!\sum_{\big\{\substack{L\in\mathcal{D}_{n_0}:\\ L\subset M}\big\}}\!\!\!\!\theta_k^La_L\Big)\mu_Mh_M.\nonumber \end{align} $$
Scalar multiplication may be replaced with tensor multiplication to obtain the same formula (i.e., consider
![]() $a_L\otimes \chi _L$
, where
$a_L\otimes \chi _L$
, where
![]() $a_L$
is, for example, in
$a_L$
is, for example, in
![]() $L_1$
).
$L_1$
).
Let us additionally observe that for any
![]() $1\leq k\leq n_0$
and
$1\leq k\leq n_0$
and
![]() $M\in \mathcal {D}_{k-1}$
, we have
$M\in \mathcal {D}_{k-1}$
, we have
 $$ \begin{align} \sum_{\big\{\substack{L\in\mathcal{D}_{n_0}\\L\subset M}\big\}}|a_L|& = \big\langle\sum_{\big\{\substack{L\in\mathcal{D}_{n_0}\\L\subset M}\big\}}|a_L|\mu_{L}\chi_L,\sum_{\big\{\substack{L\in\mathcal{D}_{n_0}\\L\subset M}\big\}}\nu_{L}\chi_L\big\rangle\\ &\leq \big\|\sum_{\big\{\substack{L\in\mathcal{D}_{n_0}\\L\subset M}\big\}}|a_L|\mu_{L}\chi_L\big\|\big\|\sum_{\big\{\substack{L\in\mathcal{D}_{n_0}\\L\subset M}\big\}}\nu_{L}\chi_L\big\|_{X^*}\nonumber\\ & \leq \big\|\sum_{L\in\mathcal{D}_{n_0}}a_L\mu_{L}\chi_L\big\|\nu_{n_0}\big\|\chi_M\big\|_{X^*}\nonumber\\ & =\nu_{n_0} \nu_{k-1}^{-1} \big\|\sum_{L\in\mathcal{D}_{n_0}}a_L\mu_{L}\chi_L\big\|.\nonumber \end{align} $$
$$ \begin{align} \sum_{\big\{\substack{L\in\mathcal{D}_{n_0}\\L\subset M}\big\}}|a_L|& = \big\langle\sum_{\big\{\substack{L\in\mathcal{D}_{n_0}\\L\subset M}\big\}}|a_L|\mu_{L}\chi_L,\sum_{\big\{\substack{L\in\mathcal{D}_{n_0}\\L\subset M}\big\}}\nu_{L}\chi_L\big\rangle\\ &\leq \big\|\sum_{\big\{\substack{L\in\mathcal{D}_{n_0}\\L\subset M}\big\}}|a_L|\mu_{L}\chi_L\big\|\big\|\sum_{\big\{\substack{L\in\mathcal{D}_{n_0}\\L\subset M}\big\}}\nu_{L}\chi_L\big\|_{X^*}\nonumber\\ & \leq \big\|\sum_{L\in\mathcal{D}_{n_0}}a_L\mu_{L}\chi_L\big\|\nu_{n_0}\big\|\chi_M\big\|_{X^*}\nonumber\\ & =\nu_{n_0} \nu_{k-1}^{-1} \big\|\sum_{L\in\mathcal{D}_{n_0}}a_L\mu_{L}\chi_L\big\|.\nonumber \end{align} $$
Proof of Proposition 6.2
For
![]() $n=0,1,\ldots $
consider the auxiliary operator
$n=0,1,\ldots $
consider the auxiliary operator
![]() $S_n = \sum _{L\in \mathcal {D}_n}T^L\otimes R^L$
, where
$S_n = \sum _{L\in \mathcal {D}_n}T^L\otimes R^L$
, where
![]() $R^L:X\to X$
denotes the restriction onto L: that is,
$R^L:X\to X$
denotes the restriction onto L: that is,
![]() $R^Lf = \chi _Lf$
. We observe that
$R^Lf = \chi _Lf$
. We observe that
 $$ \begin{align*} \|S_n - S_{n+1}\| &=\big\|\sum_{L\in\mathcal{D}_n}T^L\otimes\big(R^{L^+} + R^{L^-}\big) - \sum_{L\in\mathcal{D}_n}\big(T^{L^+}\otimes R^{L^+} + T^{L^-}\otimes R^{L^-}\big)\big\|\\ &\leq \sum_{L\in\mathcal{D}_n}\big(\|T^L - T^{L^+}\|\|R_{L^+}\| + \|T^L - T^{L^-}\|\|R^{L^-}\|\big)\\ &\leq 2\varepsilon\sum_{L\in\mathcal{D}_n}|L|^2 = \varepsilon 2^{-n+1}. \end{align*} $$
$$ \begin{align*} \|S_n - S_{n+1}\| &=\big\|\sum_{L\in\mathcal{D}_n}T^L\otimes\big(R^{L^+} + R^{L^-}\big) - \sum_{L\in\mathcal{D}_n}\big(T^{L^+}\otimes R^{L^+} + T^{L^-}\otimes R^{L^-}\big)\big\|\\ &\leq \sum_{L\in\mathcal{D}_n}\big(\|T^L - T^{L^+}\|\|R_{L^+}\| + \|T^L - T^{L^-}\|\|R^{L^-}\|\big)\\ &\leq 2\varepsilon\sum_{L\in\mathcal{D}_n}|L|^2 = \varepsilon 2^{-n+1}. \end{align*} $$
In particular, for all
![]() $n\in \mathbb {N}$
, we have
$n\in \mathbb {N}$
, we have
By equation (28), to estimate
![]() $\|T - T^\emptyset \otimes I\|$
, it is sufficient to consider vectors of the form
$\|T - T^\emptyset \otimes I\|$
, it is sufficient to consider vectors of the form
![]() $f\otimes g$
, with
$f\otimes g$
, with
![]() $f\in B_{L_1}$
,
$f\in B_{L_1}$
,
![]() $g=\sum _{L\in \mathcal {D}_{n_0}}a_L\mu _L\chi _L$
, and
$g=\sum _{L\in \mathcal {D}_{n_0}}a_L\mu _L\chi _L$
, and
![]() $\|\sum _{L\in \mathcal {D}_{n_0}}a_L\mu _L\chi _L\| = 1$
. By equation (48),
$\|\sum _{L\in \mathcal {D}_{n_0}}a_L\mu _L\chi _L\| = 1$
. By equation (48),
 $$ \begin{align} f\otimes g = \nu_{n_0}^{-1}\big(\sum_{L\in\mathcal{D}_{n_0}}a_L\big)f\otimes h_\emptyset + \nu_{n_0}^{-1}\sum_{k=1}^{n_0}\nu_{k-1}\sum_{M\in\mathcal{D}_{k-1}}\Big(\sum_{\big\{\substack{L\in\mathcal{D}_{n_0}:\\ L\subset M}\big\}}\theta_k^La_L\Big)f\otimes\mu_Mh_M.\nonumber \end{align} $$
$$ \begin{align} f\otimes g = \nu_{n_0}^{-1}\big(\sum_{L\in\mathcal{D}_{n_0}}a_L\big)f\otimes h_\emptyset + \nu_{n_0}^{-1}\sum_{k=1}^{n_0}\nu_{k-1}\sum_{M\in\mathcal{D}_{k-1}}\Big(\sum_{\big\{\substack{L\in\mathcal{D}_{n_0}:\\ L\subset M}\big\}}\theta_k^La_L\Big)f\otimes\mu_Mh_M.\nonumber \end{align} $$
From equation (50), it follows that
We next evaluate T and
![]() $S_{n_0}$
on
$S_{n_0}$
on
![]() $f\otimes g$
. Since T is X-diagonal, we have
$f\otimes g$
. Since T is X-diagonal, we have
 $$ \begin{align*} T(f\otimes g)&\stackrel{equation(51)}{=}\nu_{n_0}^{-1}\big(\!\!\!\sum_{L\in\mathcal{D}_{n_0}}\!\!\!a_L\big)\big(T^\emptyset f\big)\otimes h_\emptyset\\ &\qquad\quad + \nu_{n_0}^{-1}\sum_{k=1}^{n_0}\nu_{k-1}\!\!\!\!\sum_{M\in\mathcal{D}_{k-1}}\Big(\!\!\!\!\sum_{\big\{\substack{L\in\mathcal{D}_{n_0}:\\ L\subset M}\big\}}\!\!\!\!\theta_k^La_L\Big)\big(T^Mf\big)\otimes\mu_Mh_M. \end{align*} $$
$$ \begin{align*} T(f\otimes g)&\stackrel{equation(51)}{=}\nu_{n_0}^{-1}\big(\!\!\!\sum_{L\in\mathcal{D}_{n_0}}\!\!\!a_L\big)\big(T^\emptyset f\big)\otimes h_\emptyset\\ &\qquad\quad + \nu_{n_0}^{-1}\sum_{k=1}^{n_0}\nu_{k-1}\!\!\!\!\sum_{M\in\mathcal{D}_{k-1}}\Big(\!\!\!\!\sum_{\big\{\substack{L\in\mathcal{D}_{n_0}:\\ L\subset M}\big\}}\!\!\!\!\theta_k^La_L\Big)\big(T^Mf\big)\otimes\mu_Mh_M. \end{align*} $$
For the other valuation, note that for
![]() $L\in \mathcal {D}_{n_0}$
, we have
$L\in \mathcal {D}_{n_0}$
, we have
![]() $S_{n_0}(f\otimes \mu _L\chi _L) = \big (T^Lf\big )\otimes \mu _L\chi _L$
. Therefore,
$S_{n_0}(f\otimes \mu _L\chi _L) = \big (T^Lf\big )\otimes \mu _L\chi _L$
. Therefore,
 $$ \begin{align*} S_{n_0}(f\otimes g) &\stackrel{equation(48)}{=} \nu_{n_0}^{-1}\big(\!\!\!\sum_{L\in\mathcal{D}_{n_0}}\!\!\!a_L\big(T^Lf\big)\big)\otimes h_\emptyset\\ &\qquad\quad+ \nu_{n_0}^{-1}\sum_{k=1}^{n_0}\nu_{k-1}\!\!\!\!\sum_{M\in\mathcal{D}_{k-1}}\Big(\!\!\!\!\sum_{\big\{\substack{L\in\mathcal{D}_{n_0}:\\ L\subset M}\big\}}\!\!\!\!\theta_k^La_L\big(T^Lf\big)\Big)\otimes\mu_Mh_M. \end{align*} $$
$$ \begin{align*} S_{n_0}(f\otimes g) &\stackrel{equation(48)}{=} \nu_{n_0}^{-1}\big(\!\!\!\sum_{L\in\mathcal{D}_{n_0}}\!\!\!a_L\big(T^Lf\big)\big)\otimes h_\emptyset\\ &\qquad\quad+ \nu_{n_0}^{-1}\sum_{k=1}^{n_0}\nu_{k-1}\!\!\!\!\sum_{M\in\mathcal{D}_{k-1}}\Big(\!\!\!\!\sum_{\big\{\substack{L\in\mathcal{D}_{n_0}:\\ L\subset M}\big\}}\!\!\!\!\theta_k^La_L\big(T^Lf\big)\Big)\otimes\mu_Mh_M. \end{align*} $$
Therefore,
 $$ \begin{align*}\big\|(T - S_{n_0})(f\otimes g)\big\|\\&\leq\nu_{n_0}^{-1}\sum_{L\in\mathcal{D}_{n_0}}|a_L|\underbrace{\|T^\emptyset - T^L\|}_{\leq\varepsilon} +\nu_{n_0}^{-1}\sum_{k=1}^{n_0}\nu_{k-1}\!\!\!\!\sum_{M\in\mathcal{D}_{k-1}}\!\sum_{\big\{\substack{L\in\mathcal{D}_{n_0}:\\ L\subset M}\big\}}\!\!\!\!|a_L|\underbrace{\|T^M - T^L\|}_{\leq \varepsilon|M|^2}\\&\stackrel{equation(49)}{\leq} \nu_{n_0}^{-1}\varepsilon\underbrace{\big\|\!\!\!\sum_{L\in\mathcal{D}_{n_0}}a_L\mu_L\chi_L\big\|}_{=1}\nu_{n_0}\underbrace{\nu_0^{-1}}_{=1} \\&\qquad\quad+ \varepsilon\nu^{-1}_{n_0}\sum_{k=1}^{n_0}\nu_{k-1}\sum_{M\in\mathcal{D}_{k-1}}|M|^2\big\|\!\!\!\sum_{L\in\mathcal{D}_{n_0}}a_L\mu_L\chi_L\big\|\nu_{n_0}\nu_{k-1}^{-1}\\&= \varepsilon + \varepsilon\sum_{k=1}^{n_0}\sum_{M\in\mathcal{D}_{k-1}}|M|^2 = \varepsilon + \varepsilon\sum_{k=1}^{n_0}\frac{2^{k-1}}{2^{2k-2}} \leq 3\varepsilon.\end{align*} $$
$$ \begin{align*}\big\|(T - S_{n_0})(f\otimes g)\big\|\\&\leq\nu_{n_0}^{-1}\sum_{L\in\mathcal{D}_{n_0}}|a_L|\underbrace{\|T^\emptyset - T^L\|}_{\leq\varepsilon} +\nu_{n_0}^{-1}\sum_{k=1}^{n_0}\nu_{k-1}\!\!\!\!\sum_{M\in\mathcal{D}_{k-1}}\!\sum_{\big\{\substack{L\in\mathcal{D}_{n_0}:\\ L\subset M}\big\}}\!\!\!\!|a_L|\underbrace{\|T^M - T^L\|}_{\leq \varepsilon|M|^2}\\&\stackrel{equation(49)}{\leq} \nu_{n_0}^{-1}\varepsilon\underbrace{\big\|\!\!\!\sum_{L\in\mathcal{D}_{n_0}}a_L\mu_L\chi_L\big\|}_{=1}\nu_{n_0}\underbrace{\nu_0^{-1}}_{=1} \\&\qquad\quad+ \varepsilon\nu^{-1}_{n_0}\sum_{k=1}^{n_0}\nu_{k-1}\sum_{M\in\mathcal{D}_{k-1}}|M|^2\big\|\!\!\!\sum_{L\in\mathcal{D}_{n_0}}a_L\mu_L\chi_L\big\|\nu_{n_0}\nu_{k-1}^{-1}\\&= \varepsilon + \varepsilon\sum_{k=1}^{n_0}\sum_{M\in\mathcal{D}_{k-1}}|M|^2 = \varepsilon + \varepsilon\sum_{k=1}^{n_0}\frac{2^{k-1}}{2^{2k-2}} \leq 3\varepsilon.\end{align*} $$
In conclusion,
![]() $\|(T - T^\emptyset \otimes I)(f\otimes g)\| \leq 4\varepsilon + 3\varepsilon $
.
$\|(T - T^\emptyset \otimes I)(f\otimes g)\| \leq 4\varepsilon + 3\varepsilon $
.
We give the proof of the main result.
Proof of Theorem 6.1
Recall that by virtue of Proposition 2.3, being an approximate 1-projectional factor is a transitive property, during which the compounded errors are under control. We successively apply Theorem 4.1, Theorem 5.1 and Proposition 6.2 to find a bounded linear operator
![]() $S:L_1\to L_1$
so that T is a 1-projectional factor with error
$S:L_1\to L_1$
so that T is a 1-projectional factor with error
![]() $\varepsilon $
of
$\varepsilon $
of
![]() $S\otimes I:L_1(X)\to L_1(X)$
. By Theorem 2.9, S is a 1-projectional factor with error
$S\otimes I:L_1(X)\to L_1(X)$
. By Theorem 2.9, S is a 1-projectional factor with error
![]() $\varepsilon $
of a scalar operator
$\varepsilon $
of a scalar operator
![]() $\lambda I:L_1\to L_1$
, and therefore
$\lambda I:L_1\to L_1$
, and therefore
![]() $S\otimes I:L_1(X)\to L_1(X)$
is a 1-projectional factor with error
$S\otimes I:L_1(X)\to L_1(X)$
is a 1-projectional factor with error
![]() $\varepsilon $
of
$\varepsilon $
of
![]() $\lambda I:L_1(X)\to L_1(X)$
. Finally, T is a 1-projectional factor with error
$\lambda I:L_1(X)\to L_1(X)$
. Finally, T is a 1-projectional factor with error
![]() $2\varepsilon $
of
$2\varepsilon $
of
![]() $\lambda I:L_1(X)\to L_1(X)$
. Thus, our claim follows from Proposition 2.4.
$\lambda I:L_1(X)\to L_1(X)$
. Thus, our claim follows from Proposition 2.4.
7 Final discussion
Characterising the complemented subspaces of
![]() $L_1$
and those of
$L_1$
and those of
![]() $C(K)$
remain the most prominent problems in the study of decompositions of classical Banach spaces. This motivates in particular the study of biparameter spaces, especially those with an
$C(K)$
remain the most prominent problems in the study of decompositions of classical Banach spaces. This motivates in particular the study of biparameter spaces, especially those with an
![]() $L_1$
or
$L_1$
or
![]() $C(K)$
component. For example, the proof of primariness for each such type of space presents a different challenge and therefore an opportunity to extract new information on the structure of
$C(K)$
component. For example, the proof of primariness for each such type of space presents a different challenge and therefore an opportunity to extract new information on the structure of
![]() $L_1$
or
$L_1$
or
![]() $C(K)$
and their operators. Here is a list of classical biparameter spaces for which primariness remains unresolved:
$C(K)$
and their operators. Here is a list of classical biparameter spaces for which primariness remains unresolved:
-
(a)
 $L_p(L_1)$
for
$L_p(L_1)$
for
 $1<p\leq \infty $
.
$1<p\leq \infty $
. -
(b)
 $L_p(L_\infty )\simeq L_p(\ell _\infty )$
for
$L_p(L_\infty )\simeq L_p(\ell _\infty )$
for
 $1\leq p<\infty $
.
$1\leq p<\infty $
. -
(c)
 $\ell _p(C(K))$
for a compact metric space K and
$\ell _p(C(K))$
for a compact metric space K and
 $1\leq p\leq \infty $
.
$1\leq p\leq \infty $
. -
(d)
 $L_p(C(K))$
for a compact metric space K and
$L_p(C(K))$
for a compact metric space K and
 $1\leq p\leq \infty $
.
$1\leq p\leq \infty $
. -
(e)
 $C(K,\ell _p)$
for a compact metric space K and
$C(K,\ell _p)$
for a compact metric space K and
 $1\leq p\leq \infty $
.
$1\leq p\leq \infty $
. -
(f)
 $C(K,L_p)$
for a compact metric space K and
$C(K,L_p)$
for a compact metric space K and
 $1\leq p< \infty $
.
$1\leq p< \infty $
.
It is noteworthy that all the other biparameter Lebesgue spaces
![]() $\ell _p(\ell _q)$
[Reference Casazza, Kottman and Lin13],
$\ell _p(\ell _q)$
[Reference Casazza, Kottman and Lin13],
![]() $\ell _p(L_q)$
[Reference Capon9],
$\ell _p(L_q)$
[Reference Capon9],
![]() $\ell _p(L_1)$
[Reference Capon10],
$\ell _p(L_1)$
[Reference Capon10],
![]() $L_p(L_q)$
[Reference Capon11],
$L_p(L_q)$
[Reference Capon11],
![]() $L_p(\ell _q) $
[Reference Capon12] and
$L_p(\ell _q) $
[Reference Capon12] and
![]() $\ell _\infty (L_q) $
[Reference Wark37] (
$\ell _\infty (L_q) $
[Reference Wark37] (
![]() $1<p,q<\infty $
) are known to be primary. The space
$1<p,q<\infty $
) are known to be primary. The space
![]() $L_1(C[0,1])$
resists the approach of this paper, but perhaps some of the tools developed here could be of some use. If this were to be resolved, it is conceivable that techniques from [Reference Lechner, Motakis, Müller and Schlumprecht21] might be useful in transcending the separability barrier to show that
$L_1(C[0,1])$
resists the approach of this paper, but perhaps some of the tools developed here could be of some use. If this were to be resolved, it is conceivable that techniques from [Reference Lechner, Motakis, Müller and Schlumprecht21] might be useful in transcending the separability barrier to show that
![]() $L_1(L_\infty )$
is primary. Such methods night also be useful in the investigation of whether for nonseparable RI space
$L_1(L_\infty )$
is primary. Such methods night also be useful in the investigation of whether for nonseparable RI space
![]() $X\neq L_\infty $
,
$X\neq L_\infty $
,
![]() $L_1(X)$
is primary. In more generality, one may ask for what types of Banach spaces X the spaces
$L_1(X)$
is primary. In more generality, one may ask for what types of Banach spaces X the spaces
![]() $L_1(X)$
,
$L_1(X)$
,
![]() $L_p(X)$
,
$L_p(X)$
,
![]() $H_1(X)$
and
$H_1(X)$
and
![]() $H_p(X)$
are primary.
$H_p(X)$
are primary.
For any two rearrangement-invariant Banach function spaces X and Y on
![]() $[0,1]$
, one can define the biparameter space
$[0,1]$
, one can define the biparameter space
![]() $X(Y)$
as the space of all functions
$X(Y)$
as the space of all functions
![]() $f:[0,1]^2\to \mathbb C$
for which
$f:[0,1]^2\to \mathbb C$
for which
![]() $f(s,\cdot )\in Y$
for all
$f(s,\cdot )\in Y$
for all
![]() $s\in [0,1]$
and
$s\in [0,1]$
and
![]() $g=g_f: [0,1]\to \mathbb {R}$
,
$g=g_f: [0,1]\to \mathbb {R}$
,
![]() $s\mapsto \|f(s,\cdot )\|_Y$
is in X. The norm of f in
$s\mapsto \|f(s,\cdot )\|_Y$
is in X. The norm of f in
![]() $X(Y)$
would then be
$X(Y)$
would then be
![]() $\|f\|_{X(Y)} = \| g_f\|_X$
. It would be interesting to formulate general conditions on X and Y, which imply that
$\|f\|_{X(Y)} = \| g_f\|_X$
. It would be interesting to formulate general conditions on X and Y, which imply that
![]() $X(Y)$
is primary or has the factorisation property (formulated below) with respect to some basis.
$X(Y)$
is primary or has the factorisation property (formulated below) with respect to some basis.
The above list may be expanded to the tri-parameter spaces, in which setting there has been little progress.
It is natural to study general conditions under which an operator T on a Banach space is a factor of the identity. A bounded linear operator T on a Banach space X with a Schauder basis
![]() $(e_n)_n$
is said to have large diagonal if
$(e_n)_n$
is said to have large diagonal if
![]() $\inf _n|e_n^*(Te_n)|> 0$
. If every operator on X with large diagonal is a factor of the identity, then we say that X has the factorisation property. The study of the factorisation property and that of primariness are closely related. Our proof does not directly show that the spaces under investigation have the factorisation property. We may therefore ask: for what Haar system spaces X and Y does the biparameter Haar system
$\inf _n|e_n^*(Te_n)|> 0$
. If every operator on X with large diagonal is a factor of the identity, then we say that X has the factorisation property. The study of the factorisation property and that of primariness are closely related. Our proof does not directly show that the spaces under investigation have the factorisation property. We may therefore ask: for what Haar system spaces X and Y does the biparameter Haar system
![]() $(h_I\otimes h_L)_{(I,L)\in \mathcal {D}^+\times \mathcal {D}^+}$
have the factorisation property in
$(h_I\otimes h_L)_{(I,L)\in \mathcal {D}^+\times \mathcal {D}^+}$
have the factorisation property in
![]() $X(Y)$
?
$X(Y)$
?
Acknowledgements
We would like to thank the anonymous referee for very helpful suggestions on how to improve the presentation of our paper.
Funding statement
The first author was supported by the Austrian Science Foundation (FWF) under Grant Number Pr.Nr. P32728. The second author was supported by NSERC Grant RGPIN-2021-03639. The third author was supported by the Austrian Science Foundation (FWF) under Project Numbers P344114 and I-5231. The fourth author was supported by the National Science Foundation under Grant Numbers DMS-1764343 and DMS-2054443.
Conflict of Interest
None.