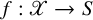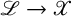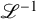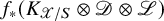1 Introduction
We consider a proper holomorphic submersion ![]() $f: \mathscr {X} \to S$ of complex manifolds and a snc divisor
$f: \mathscr {X} \to S$ of complex manifolds and a snc divisor ![]() $\mathscr {D}$ on
$\mathscr {D}$ on ![]() $\mathscr {X}$ whose restriction
$\mathscr {X}$ whose restriction ![]() $D_s:=\mathscr {D}|_{X_s}$ to each fibre
$D_s:=\mathscr {D}|_{X_s}$ to each fibre ![]() $X_s=f^{-1}(s)$ is also simple normal crossing. Given a line bundle
$X_s=f^{-1}(s)$ is also simple normal crossing. Given a line bundle ![]() $\mathscr {L} \to \mathscr {X}$ that carries a hermitian metric that is smooth on
$\mathscr {L} \to \mathscr {X}$ that carries a hermitian metric that is smooth on ![]() $\mathscr {X}':= \mathscr {X} \setminus \mathscr {D}$ and whose inverse has Poincaré growth near the divisor
$\mathscr {X}':= \mathscr {X} \setminus \mathscr {D}$ and whose inverse has Poincaré growth near the divisor ![]() $\mathscr {D}$, we study the spaces of square integrable canonical forms on the open fibres
$\mathscr {D}$, we study the spaces of square integrable canonical forms on the open fibres ![]() $X^{\prime }_s:= X_s \setminus D_s$ that have values in
$X^{\prime }_s:= X_s \setminus D_s$ that have values in ![]() $L_s:=\mathscr {L}|_{X^{\prime }_s}$. By the work of Zucker [Reference Zucker24] and Fujiki [Reference Fujiki8], we can identify these
$L_s:=\mathscr {L}|_{X^{\prime }_s}$. By the work of Zucker [Reference Zucker24] and Fujiki [Reference Fujiki8], we can identify these ![]() $L^2$-Dolbeault cohomology groups
$L^2$-Dolbeault cohomology groups ![]() $H^0_{(2)}(X^{\prime }_s,K_{X^{\prime }_s}\otimes L_s)$ with the spaces
$H^0_{(2)}(X^{\prime }_s,K_{X^{\prime }_s}\otimes L_s)$ with the spaces ![]() $H^0(X_s,K_{X_s}\otimes D_s\otimes L_s)$. More globally, we will see that these spaces are the fibres of the coherent sheaf
$H^0(X_s,K_{X_s}\otimes D_s\otimes L_s)$. More globally, we will see that these spaces are the fibres of the coherent sheaf ![]() $f_*(K_{\mathscr {X}/S}\otimes \mathscr {D} \otimes \mathscr {L})$ on the base S. Under the condition that this sheaf is locally free, the natural
$f_*(K_{\mathscr {X}/S}\otimes \mathscr {D} \otimes \mathscr {L})$ on the base S. Under the condition that this sheaf is locally free, the natural ![]() $L^2$-metrics on the
$L^2$-metrics on the ![]() $L^2$-Dolbeault spaces induce a smooth hermitian metric on the direct image. We give an explicit curvature formula for it in the case the hermitian metric on
$L^2$-Dolbeault spaces induce a smooth hermitian metric on the direct image. We give an explicit curvature formula for it in the case the hermitian metric on ![]() $\mathscr {L}$ is positive along the fibres
$\mathscr {L}$ is positive along the fibres ![]() $X^{\prime }_s$. If
$X^{\prime }_s$. If ![]() $\mathscr {L}$ is globally positive on
$\mathscr {L}$ is globally positive on ![]() $\mathscr {X}':=\mathscr {X} \setminus \mathscr {D}$, the direct image
$\mathscr {X}':=\mathscr {X} \setminus \mathscr {D}$, the direct image ![]() $f_*(K_{\mathscr {X}/S}\otimes \mathscr {D} \otimes \mathscr {L})$ is also positive. The result applies to families of log-canonically polarized pairs, where the Poincaré type Kähler-Einstein metrics induce such a singular hermitian metric on the relative canonical bundle. We give another application to illustrate how our result improves the general positivity theorem from [Reference Berndtsson and Păun3] in a special situation.
$f_*(K_{\mathscr {X}/S}\otimes \mathscr {D} \otimes \mathscr {L})$ is also positive. The result applies to families of log-canonically polarized pairs, where the Poincaré type Kähler-Einstein metrics induce such a singular hermitian metric on the relative canonical bundle. We give another application to illustrate how our result improves the general positivity theorem from [Reference Berndtsson and Păun3] in a special situation.
2 Differential geometric setup and statement of results
Let ![]() $f: \mathscr {X} \to S$ be a proper holomorphic submersion of complex manifolds with connected fibres and
$f: \mathscr {X} \to S$ be a proper holomorphic submersion of complex manifolds with connected fibres and ![]() $\mathscr {L}$ a line bundle on
$\mathscr {L}$ a line bundle on ![]() $\mathscr {X}$. We assume that
$\mathscr {X}$. We assume that ![]() $\mathscr {L}$ has a hermitian metric h that is smooth on the complement of a relative simple normal crossing divisor
$\mathscr {L}$ has a hermitian metric h that is smooth on the complement of a relative simple normal crossing divisor ![]() $\mathscr {D}=\sum _{i=1}^l{\mathscr {D}_i}$ on
$\mathscr {D}=\sum _{i=1}^l{\mathscr {D}_i}$ on ![]() $\mathscr {X}$ with the following asymptotic behaviour along
$\mathscr {X}$ with the following asymptotic behaviour along ![]() $\mathscr {D}$
$\mathscr {D}$
 $$ \begin{align} h^{-1}|_{\mathscr{X}'}= \exp(u)\cdot \frac{h_{\mathscr{L}^{-1}}^{C^{\infty}}}{\prod_{i=1}^l{||\sigma_i||_i^2\log^2||\sigma_i||_i^2}}, \end{align} $$
$$ \begin{align} h^{-1}|_{\mathscr{X}'}= \exp(u)\cdot \frac{h_{\mathscr{L}^{-1}}^{C^{\infty}}}{\prod_{i=1}^l{||\sigma_i||_i^2\log^2||\sigma_i||_i^2}}, \end{align} $$where the notation is as follows:
•
 $h_{\mathscr {L}^{-1}}^{C^{\infty }}$ is a smooth metric on
$h_{\mathscr {L}^{-1}}^{C^{\infty }}$ is a smooth metric on  $\mathscr {L}^{-1}$.
$\mathscr {L}^{-1}$.•
 $||\sigma _i||_i$ is the norm of the canonical section cutting out
$||\sigma _i||_i$ is the norm of the canonical section cutting out  $\mathcal {D}_i$ with regard to a smooth metric s.t.
$\mathcal {D}_i$ with regard to a smooth metric s.t.  $||\sigma _i||_i<1$.
$||\sigma _i||_i<1$.• u is a function on
 $\mathscr {X}'$ s.t.
$\mathscr {X}'$ s.t.  $u|_{X^{\prime }_s} \in \mathscr {C}^{k,\alpha }$ (
$u|_{X^{\prime }_s} \in \mathscr {C}^{k,\alpha }$ ( $k\geq 2$) for all s, and the map
$k\geq 2$) for all s, and the map  $s \mapsto u|_{X^{\prime }_s}$ is Fréchet differentiable.
$s \mapsto u|_{X^{\prime }_s}$ is Fréchet differentiable.•
 $\omega _s:= -\mathrm {i} \partial \bar \partial \log (h)|_{X^{\prime }_s}$ is a Poincaré type Kähler metric on each fibre
$\omega _s:= -\mathrm {i} \partial \bar \partial \log (h)|_{X^{\prime }_s}$ is a Poincaré type Kähler metric on each fibre  $X^{\prime }_s$.
$X^{\prime }_s$.
Here we have used the Hölder space of functions ![]() $\mathscr {C}^{k,\alpha }=\mathscr {C}^{k,\alpha }(X_{s_0}')$ on an open fibre
$\mathscr {C}^{k,\alpha }=\mathscr {C}^{k,\alpha }(X_{s_0}')$ on an open fibre ![]() $X^{\prime }_{s_0}$ that were introduced in [Reference Cheng and Yau6, Reference Kobayashi14, Reference Tian, Yau, Yau and Diego21] and do not depend on the fibre. We refer to this by saying that the inverse metric
$X^{\prime }_{s_0}$ that were introduced in [Reference Cheng and Yau6, Reference Kobayashi14, Reference Tian, Yau, Yau and Diego21] and do not depend on the fibre. We refer to this by saying that the inverse metric ![]() $h^{-1}$ has Poincaré type singularities along
$h^{-1}$ has Poincaré type singularities along ![]() $\mathscr {D}$. We write
$\mathscr {D}$. We write ![]() $\mathscr {D} \overset {i}{\hookrightarrow } \mathscr {X} \overset {f}{\rightarrow } S$ for the family of smooth log pairs
$\mathscr {D} \overset {i}{\hookrightarrow } \mathscr {X} \overset {f}{\rightarrow } S$ for the family of smooth log pairs ![]() $(X_s,D_s)$.
$(X_s,D_s)$.
The reason for choosing this asymptotic will become clear when we consider the family of Poincaré type Kähler-Einstein metrics for a family of log canonically polarized manifolds. We remark that it includes the case where the function u is smooth on ![]() $\mathscr {X}$, and it implies that u and its derivatives in the base and fibre direction we will consider are bounded on
$\mathscr {X}$, and it implies that u and its derivatives in the base and fibre direction we will consider are bounded on ![]() $\mathscr {X}'$. In a local description, the norm squared of a local trivialising section
$\mathscr {X}'$. In a local description, the norm squared of a local trivialising section ![]() $e_{\mathscr {L}}$ of
$e_{\mathscr {L}}$ of ![]() $\mathscr {L}$ near a point
$\mathscr {L}$ near a point ![]() $p\in \mathscr {D}$ is given by
$p\in \mathscr {D}$ is given by
 $$ \begin{align*} |e_{\mathscr{L}}|^2_{h}(z,s)=\left( \prod_{i=1}^r{|z^i|^2\log^2(|z^i|^2)}\right) \cdot v(z,s), \quad v \in C^k_{\operatorname{loc}}(\mathscr{X}'), \end{align*} $$
$$ \begin{align*} |e_{\mathscr{L}}|^2_{h}(z,s)=\left( \prod_{i=1}^r{|z^i|^2\log^2(|z^i|^2)}\right) \cdot v(z,s), \quad v \in C^k_{\operatorname{loc}}(\mathscr{X}'), \end{align*} $$where the divisor is given by ![]() $\mathscr {D}=\{ z^1\cdots z^r=0\}$ with respect to local holomorphic coordinates
$\mathscr {D}=\{ z^1\cdots z^r=0\}$ with respect to local holomorphic coordinates ![]() $(z,s)$ around p with
$(z,s)$ around p with ![]() $z=z^1,\ldots ,z^n$ and
$z=z^1,\ldots ,z^n$ and ![]() $s=s^1,\dots ,s^m$ such that
$s=s^1,\dots ,s^m$ such that ![]() $f(z,s)=s$. Here,
$f(z,s)=s$. Here, ![]() $n:= \dim X_s$ and
$n:= \dim X_s$ and ![]() $m:= \dim S$.
$m:= \dim S$.
The curvature form of the hermitian line bundle ![]() $(\mathscr {L},h)$ restricted to
$(\mathscr {L},h)$ restricted to ![]() $\mathscr {X}':=\mathscr {X}\setminus \mathscr {D}$ is given by
$\mathscr {X}':=\mathscr {X}\setminus \mathscr {D}$ is given by
This means we view h as a singular hermitian metric on ![]() $\mathscr {L}$ whose curvature current restricted to
$\mathscr {L}$ whose curvature current restricted to ![]() $\mathscr {X}'$ is given by the smooth form
$\mathscr {X}'$ is given by the smooth form ![]() $\omega _{\mathscr {X}'}$. Our assumption on h guarantees that each restriction
$\omega _{\mathscr {X}'}$. Our assumption on h guarantees that each restriction ![]() $\omega _{\mathscr {X}'}|_{X_s'}$ is quasi-isometric to the model metric
$\omega _{\mathscr {X}'}|_{X_s'}$ is quasi-isometric to the model metric
 $$ \begin{align*} \sqrt{-1}\left( \sum_{i=1}^k{\frac{dz^i\wedge d\overline{z}^i}{|z^i|^2\log^2(1/|z^i|^2)}} + \sum_{i=k+1}^n{dz^i\wedge d\overline{z}^i} \right) \end{align*} $$
$$ \begin{align*} \sqrt{-1}\left( \sum_{i=1}^k{\frac{dz^i\wedge d\overline{z}^i}{|z^i|^2\log^2(1/|z^i|^2)}} + \sum_{i=k+1}^n{dz^i\wedge d\overline{z}^i} \right) \end{align*} $$near the point p.
We consider the case where the hermitian line bundle ![]() $(\mathscr {L},h)|_{\mathscr {X}'}$ is relatively positive, which means
$(\mathscr {L},h)|_{\mathscr {X}'}$ is relatively positive, which means
are Kähler forms on the open fibres ![]() $X^{\prime }_s:=X_s\setminus D_s$. This implies that
$X^{\prime }_s:=X_s\setminus D_s$. This implies that ![]() $\mathscr {L}\otimes \mathscr {D}$ is relatively big and nef. Then one has the notion of the horizontal lift
$\mathscr {L}\otimes \mathscr {D}$ is relatively big and nef. Then one has the notion of the horizontal lift ![]() $v_i$ of a tangent vector
$v_i$ of a tangent vector ![]() $ \partial _i$ on the base S (see Section 6.1 for the precise definition), and we get a representative of the Kodaira-Spencer class by
$ \partial _i$ on the base S (see Section 6.1 for the precise definition), and we get a representative of the Kodaira-Spencer class by
which is a ![]() $\mathscr {C}^{k,\alpha }$-tensor by [Reference Schumacher18, Lemma 3] and thus square integrable. Furthermore, one sets
$\mathscr {C}^{k,\alpha }$-tensor by [Reference Schumacher18, Lemma 3] and thus square integrable. Furthermore, one sets
which is called the geodesic curvature. We note that ![]() $(\varphi _{i\overline {\jmath }})_{i\overline {\jmath }}$ is positive (semi-)definite if and only if
$(\varphi _{i\overline {\jmath }})_{i\overline {\jmath }}$ is positive (semi-)definite if and only if ![]() $\mathscr {L}$ is globally (semi-)positive on
$\mathscr {L}$ is globally (semi-)positive on ![]() $\mathscr {X}'$. Again, our assumption on
$\mathscr {X}'$. Again, our assumption on ![]() $u(z,s)$ guarantees that each
$u(z,s)$ guarantees that each ![]() $\varphi _{i\overline {\jmath }}$ is a
$\varphi _{i\overline {\jmath }}$ is a ![]() $\mathscr {C}^{k,\alpha }$ function and thus in particular bounded on each fibre.
$\mathscr {C}^{k,\alpha }$ function and thus in particular bounded on each fibre.
Now we turn to the direct image sheaf we want to study. On a fibre ![]() $X_s$, we denote by
$X_s$, we denote by ![]() $\Omega ^n_{X_s}(\log D_s)=K_{X_s}\otimes D_s$ the locally free sheaf of germs of logarithmic n-forms with log-poles along
$\Omega ^n_{X_s}(\log D_s)=K_{X_s}\otimes D_s$ the locally free sheaf of germs of logarithmic n-forms with log-poles along ![]() $D_s$. This sheaf is the restriction of
$D_s$. This sheaf is the restriction of ![]() $\Omega ^n(\log \mathscr {D})_{\mathscr {X}/S}=K_{\mathscr {X}/S}\otimes \mathscr {D}$, the sheaf of relative logarithmic n-forms with log-poles along
$\Omega ^n(\log \mathscr {D})_{\mathscr {X}/S}=K_{\mathscr {X}/S}\otimes \mathscr {D}$, the sheaf of relative logarithmic n-forms with log-poles along ![]() $\mathscr {D}$, to the fibres
$\mathscr {D}$, to the fibres ![]() $X_s$.
$X_s$.
We assume that the dimension of the cohomology groups
is constant on S, which in general only holds outside a proper subvariety. Under this assumption, we get the local freeness of the coherent sheaf
whose fibres are canonically isomorphic to the cohomology groups ![]() $H^0(X_s,\Omega ^n_{X_s}(\log D_s)(L_s))$. By the work of Zucker [Reference Zucker24] and Fujiki [Reference Fujiki8], we can identify these groups with the
$H^0(X_s,\Omega ^n_{X_s}(\log D_s)(L_s))$. By the work of Zucker [Reference Zucker24] and Fujiki [Reference Fujiki8], we can identify these groups with the ![]() $L^2$-Dolbeault cohomology groups
$L^2$-Dolbeault cohomology groups ![]() $H^0_{(2)}(X^{\prime }_s,K_{X^{\prime }_s}\otimes L_s)$. Hence, the latter spaces also form a vector bundle on the base, which we denote by
$H^0_{(2)}(X^{\prime }_s,K_{X^{\prime }_s}\otimes L_s)$. Hence, the latter spaces also form a vector bundle on the base, which we denote by
It turns out that this is nothing but the bundle ![]() $f_*(\Omega ^n(\log \mathscr {D})_{\mathscr {X}/S}(\mathscr {L}))$. Now we can represent local sections of this bundle by holomorphic sections of
$f_*(\Omega ^n(\log \mathscr {D})_{\mathscr {X}/S}(\mathscr {L}))$. Now we can represent local sections of this bundle by holomorphic sections of ![]() $\Omega ^n(\log \mathscr {D})_{\mathscr {X}/S}(\mathscr {L})$ whose restrictions to the open fibres
$\Omega ^n(\log \mathscr {D})_{\mathscr {X}/S}(\mathscr {L})$ whose restrictions to the open fibres ![]() $X^{\prime }_s$ are thus
$X^{\prime }_s$ are thus ![]() $L^2$-integrable and holomorphic
$L^2$-integrable and holomorphic ![]() $(n,0)$-forms with values in
$(n,0)$-forms with values in ![]() $L_s$. Let
$L_s$. Let ![]() $\{\psi ^1,\ldots ,\psi ^r\}$ be a local frame of the direct image consisting of such sections around a fixed point
$\{\psi ^1,\ldots ,\psi ^r\}$ be a local frame of the direct image consisting of such sections around a fixed point ![]() $s \in S$. We denote by
$s \in S$. We denote by ![]() $\{( \partial / \partial s_i)\;|\;i=1,\ldots ,m\}$ a basis of the complex tangent space
$\{( \partial / \partial s_i)\;|\;i=1,\ldots ,m\}$ a basis of the complex tangent space ![]() $T_sS$ of S over
$T_sS$ of S over ![]() $\mathbb {C}$, where
$\mathbb {C}$, where ![]() $s_i$ are local holomorphic coordinates on S. The components of the metric tensor for the
$s_i$ are local holomorphic coordinates on S. The components of the metric tensor for the ![]() $L^2$-metric on the direct image are then defined by
$L^2$-metric on the direct image are then defined by
 $$ \begin{align*} H^{\overline{l} k}(s):={\langle}\psi^k,\psi^l{\rangle} :={\langle}\psi^k|_{X^{\prime}_s},\psi^l|_{X^{\prime}_s}{\rangle}(s) := \int_{X^{\prime}_s}{\psi^k|_{X^{\prime}_s} \cdot \psi^{\overline{l}}|_{X^{\prime}_s}\; dV} = \mathrm{i}^{n^2} \int_{X^{\prime}_s}{(\psi^k|_{X^{\prime}_s} \wedge \psi^{\overline{l}}|_{X^{\prime}_s})_h}. \end{align*} $$
$$ \begin{align*} H^{\overline{l} k}(s):={\langle}\psi^k,\psi^l{\rangle} :={\langle}\psi^k|_{X^{\prime}_s},\psi^l|_{X^{\prime}_s}{\rangle}(s) := \int_{X^{\prime}_s}{\psi^k|_{X^{\prime}_s} \cdot \psi^{\overline{l}}|_{X^{\prime}_s}\; dV} = \mathrm{i}^{n^2} \int_{X^{\prime}_s}{(\psi^k|_{X^{\prime}_s} \wedge \psi^{\overline{l}}|_{X^{\prime}_s})_h}. \end{align*} $$Here we use the notation ![]() $\psi ^{\overline {l}}:=\overline {\psi ^l}$ for the sections
$\psi ^{\overline {l}}:=\overline {\psi ^l}$ for the sections ![]() $\psi ^l$ and write
$\psi ^l$ and write ![]() $dV =\omega _{X^{\prime }_s}^n/n!$. The pointwise inner product
$dV =\omega _{X^{\prime }_s}^n/n!$. The pointwise inner product ![]() $\psi ^k \cdot \psi ^{\overline {l}}$ is the one given by
$\psi ^k \cdot \psi ^{\overline {l}}$ is the one given by ![]() $\omega _s$ and
$\omega _s$ and ![]() $h|_{X_s'}$. In the last equality, we used the Hodge-Riemann bilinear relation because the holomorphic
$h|_{X_s'}$. In the last equality, we used the Hodge-Riemann bilinear relation because the holomorphic ![]() $(n,0)$-forms are primitive. Note that by working on the open fibres
$(n,0)$-forms are primitive. Note that by working on the open fibres ![]() $X_s'$, the metrics involved are smooth so that we have a harmonic theory for square integrable forms lying in the domain of the Laplacian.
$X_s'$, the metrics involved are smooth so that we have a harmonic theory for square integrable forms lying in the domain of the Laplacian.
Let ![]() $A_{i\overline {\beta }}^{\alpha }(z,s) \partial _{\alpha }dz^{\overline {\beta }}=\bar \partial (v_i)|_{X^{\prime }_s}$ be the
$A_{i\overline {\beta }}^{\alpha }(z,s) \partial _{\alpha }dz^{\overline {\beta }}=\bar \partial (v_i)|_{X^{\prime }_s}$ be the ![]() $\bar \partial $-closed representative of the Kodaira-Spencer class of
$\bar \partial $-closed representative of the Kodaira-Spencer class of ![]() $ \partial _i$ described above. We know that
$ \partial _i$ described above. We know that ![]() $A_i$ lies in the space of smooth and
$A_i$ lies in the space of smooth and ![]() $L^2$-integrable
$L^2$-integrable ![]() $(0,1)$-forms
$(0,1)$-forms ![]() $A^{0,1}_{(2)}(X^{\prime }_s,T_{X^{\prime }_s})$. Hence these, together with contraction, define a map
$A^{0,1}_{(2)}(X^{\prime }_s,T_{X^{\prime }_s})$. Hence these, together with contraction, define a map
When applying the Laplace operator to ![]() $(p,q)$-forms with values in
$(p,q)$-forms with values in ![]() $L|_{X^{\prime }_s}$ on the fibres
$L|_{X^{\prime }_s}$ on the fibres ![]() $X^{\prime }_s$, we have
$X^{\prime }_s$, we have
due to the definition ![]() $\omega _{X^{\prime }_s}=\omega _{\mathscr {X}'}|_{X^{\prime }_s}$ and the Bochner-Kodaira-Nakano identity. Thus, we write
$\omega _{X^{\prime }_s}=\omega _{\mathscr {X}'}|_{X^{\prime }_s}$ and the Bochner-Kodaira-Nakano identity. Thus, we write ![]() $\Box =\Box _{\partial }=\Box _{\bar \partial }$ in the case
$\Box =\Box _{\partial }=\Box _{\bar \partial }$ in the case ![]() $q=n-p$. The main result is
$q=n-p$. The main result is
Theorem 2.1. Let ![]() $\mathscr {D} \overset {i}{\hookrightarrow } \mathscr {X} \overset {f}{\rightarrow } S$ be a family of smooth log pairs and
$\mathscr {D} \overset {i}{\hookrightarrow } \mathscr {X} \overset {f}{\rightarrow } S$ be a family of smooth log pairs and ![]() $(\mathscr {L},h)\to \mathscr {X}$ a hermitian line bundle as described above. With the objects just described, the
$(\mathscr {L},h)\to \mathscr {X}$ a hermitian line bundle as described above. With the objects just described, the ![]() $L^2$-metric on
$L^2$-metric on ![]() $f_*(\Omega ^n(\log \mathscr {D})_{\mathscr {X}/S}(\mathscr {L}))$ is smooth, and its curvature is given by
$f_*(\Omega ^n(\log \mathscr {D})_{\mathscr {X}/S}(\mathscr {L}))$ is smooth, and its curvature is given by
 $$ \begin{align*} R_{i\overline{\jmath}}^{\overline{l} k}(s) &= \int_{X^{\prime}_s}{\varphi_{i\overline{\jmath}} \cdot(\psi^k\cdot\psi^{\overline{l}})\,dV}\\ &\quad + \int_{X^{\prime}_s}{(\Box +1)^{-1}(A_i \cup \psi^k)\cdot(A_{\overline{\jmath}}\cup\psi^{\overline{l}})\,dV}. \end{align*} $$
$$ \begin{align*} R_{i\overline{\jmath}}^{\overline{l} k}(s) &= \int_{X^{\prime}_s}{\varphi_{i\overline{\jmath}} \cdot(\psi^k\cdot\psi^{\overline{l}})\,dV}\\ &\quad + \int_{X^{\prime}_s}{(\Box +1)^{-1}(A_i \cup \psi^k)\cdot(A_{\overline{\jmath}}\cup\psi^{\overline{l}})\,dV}. \end{align*} $$In particular, ![]() $f_*(K_{\mathscr {X}/S}\otimes \mathscr {D} \otimes \mathscr {L})$ is Nakano (semi-)positive if
$f_*(K_{\mathscr {X}/S}\otimes \mathscr {D} \otimes \mathscr {L})$ is Nakano (semi-)positive if ![]() $\mathscr {L}$ is (semi-)positive on
$\mathscr {L}$ is (semi-)positive on ![]() $\mathscr {X}'$ and positive along the fibres
$\mathscr {X}'$ and positive along the fibres ![]() $X^{\prime }_s$.
$X^{\prime }_s$.
We remark that if ![]() $\mathscr {L}$ is (semi-)positive, the direct image
$\mathscr {L}$ is (semi-)positive, the direct image ![]() $f_*(K_{\mathscr {X}/S}\otimes \mathscr {D} \otimes \mathscr {L})$ is locally free by the Ohsawa-Takegoshi extension theorem. The result applies to families of log-canonically polarized pairs where the relative canonical bundle
$f_*(K_{\mathscr {X}/S}\otimes \mathscr {D} \otimes \mathscr {L})$ is locally free by the Ohsawa-Takegoshi extension theorem. The result applies to families of log-canonically polarized pairs where the relative canonical bundle ![]() $K_{\mathscr {X}'/S}$ plays the role of
$K_{\mathscr {X}'/S}$ plays the role of ![]() $\mathscr {L}$. Here the hermitian metric is induced from the fibrewise Poincaré type Kähler-Einstein metrics. In this case, we first prove
$\mathscr {L}$. Here the hermitian metric is induced from the fibrewise Poincaré type Kähler-Einstein metrics. In this case, we first prove
Theorem 2.2 ( $=$ Theorem 4.1).
$=$ Theorem 4.1).
Let ![]() $\mathscr {D} \overset {i}{\hookrightarrow } \mathscr {X} \overset {f}{\rightarrow } S$ be a family of smooth log-canonically polarized pairs. Then the curvature of the hermitian metric on
$\mathscr {D} \overset {i}{\hookrightarrow } \mathscr {X} \overset {f}{\rightarrow } S$ be a family of smooth log-canonically polarized pairs. Then the curvature of the hermitian metric on ![]() $K_{\mathscr {X}'/S}$ that is induced by the Poincaré type Kähler-Einstein metrics on the fibres is semipositive. If the family is effectively parametrised, then
$K_{\mathscr {X}'/S}$ that is induced by the Poincaré type Kähler-Einstein metrics on the fibres is semipositive. If the family is effectively parametrised, then ![]() $K_{\mathscr {X}'/S}$ is strictly positive.
$K_{\mathscr {X}'/S}$ is strictly positive.
This answers a question raised in [Reference Guenancia11, Remark 7.1]:
Corollary 1 ( $=$ Corollary 5).
$=$ Corollary 5).
For a family of smooth log-canonically polarized pairs ![]() $\mathscr {D} \overset {i}{\hookrightarrow } \mathscr {X} \overset {f}{\rightarrow } S$, the relative log-canonical bundle
$\mathscr {D} \overset {i}{\hookrightarrow } \mathscr {X} \overset {f}{\rightarrow } S$, the relative log-canonical bundle ![]() $K_{\mathscr {X}/S}\otimes \mathscr {D}$ equipped with the metric induced from the fibrewise Kähler-Einstein metrics is nef. If the family is effectively parametrised,
$K_{\mathscr {X}/S}\otimes \mathscr {D}$ equipped with the metric induced from the fibrewise Kähler-Einstein metrics is nef. If the family is effectively parametrised, ![]() $K_{\mathscr {X}/S}\otimes \mathscr {D}$ is big. Here, S is assumed to be compact.
$K_{\mathscr {X}/S}\otimes \mathscr {D}$ is big. Here, S is assumed to be compact.
By combining both theorems, we get
Corollary 2. For a family of log-canonically polarized pairs ![]() $\mathscr {D} \overset {i}{\hookrightarrow } \mathscr {X} \overset {f}{\rightarrow } S$, the direct image sheaf
$\mathscr {D} \overset {i}{\hookrightarrow } \mathscr {X} \overset {f}{\rightarrow } S$, the direct image sheaf ![]() $f_*((K_{\mathscr {X}/S}\otimes \mathscr {D})\otimes K_{\mathscr {X}/S})$ is semipositive in the sense of Nakano. If the family of log pairs is effectively parametrised, this direct image is Nakano positive.
$f_*((K_{\mathscr {X}/S}\otimes \mathscr {D})\otimes K_{\mathscr {X}/S})$ is semipositive in the sense of Nakano. If the family of log pairs is effectively parametrised, this direct image is Nakano positive.
To implement the method of computation given in [Reference Schumacher19, Reference Naumann17], we have to pass from the compact fibres ![]() $X_s$ to the open part
$X_s$ to the open part ![]() $X^{\prime }_s$, where the metrics in consideration are smooth. This requires imposing the
$X^{\prime }_s$, where the metrics in consideration are smooth. This requires imposing the ![]() $L^2$ condition on the spaces of forms on
$L^2$ condition on the spaces of forms on ![]() $X^{\prime }_s$. To show that all steps in the computation are still justified, we have to check integrability. This is possible due to knowledge of the asymptotic behaviour of our sections. Hölder spaces are another important tool with respect to quasi-coordinates. We give the details below.
$X^{\prime }_s$. To show that all steps in the computation are still justified, we have to check integrability. This is possible due to knowledge of the asymptotic behaviour of our sections. Hölder spaces are another important tool with respect to quasi-coordinates. We give the details below.
A proof of the more general curvature formula, including the higher direct images, was claimed in [Reference To and Yeung22]. However, the arguments in this work seem to be incomplete. One major issue is the smooth dependency of the fibrewise harmonic projections without the usual assumption of having constant dimension for the space of fibrewise harmonic forms; compare to [Reference To and Yeung22, Lemma 2]. This is impossible given that linear independency is an open property; compare to the argument in the proof of [Reference Kodaira15, Lemma 7.7]. Moreover, it is unclear how to derive the square integrability of some Lie-differentiated forms from the arguments given in [Reference To and Yeung22, pp. 2958f], which is another key ingredient in the computation. In the present independent work, we give the detailed arguments for the case of the zeroth direct image. The key is that one has a precise asymptotic for square integrable holomorphic sections due to the Laurent series expansion that is lacking for the case of general harmonic forms.
3 Preparations
3.1  $L^2$-integrable forms
$L^2$-integrable forms
We start with a fibrewise consideration. Let ![]() $(X,D=\sum _{i=1}^lD_i)$ be a smooth log pair, and set
$(X,D=\sum _{i=1}^lD_i)$ be a smooth log pair, and set ![]() $X'=X\backslash D$. We consider a holomorphic line bundle L on X together with a metric h that is smooth on
$X'=X\backslash D$. We consider a holomorphic line bundle L on X together with a metric h that is smooth on ![]() $X'$ and whose inverse has the asymptotic behaviour from equation (2.1)
$X'$ and whose inverse has the asymptotic behaviour from equation (2.1)
 $$ \begin{align*} h^{-1}|_{X'}= \exp(u)\cdot \frac{h_{L^{-1}}^{C^{\infty}}}{\prod_{i=1}^l{||\sigma_i||_i^2\log^2||\sigma_i||_i^2}}, \end{align*} $$
$$ \begin{align*} h^{-1}|_{X'}= \exp(u)\cdot \frac{h_{L^{-1}}^{C^{\infty}}}{\prod_{i=1}^l{||\sigma_i||_i^2\log^2||\sigma_i||_i^2}}, \end{align*} $$where the notation is as follows:
•
 $h_{L^{-1}}^{C^{\infty }}$ is a smooth metric on
$h_{L^{-1}}^{C^{\infty }}$ is a smooth metric on  $\mathscr {L}^{-1}$.
$\mathscr {L}^{-1}$.•
 $||\sigma _i||_i$ is the norm of the canonical section cutting out
$||\sigma _i||_i$ is the norm of the canonical section cutting out  $D_i$ with regard to a smooth metric s.t.
$D_i$ with regard to a smooth metric s.t.  $||\sigma _i||_i<1$.
$||\sigma _i||_i<1$.• u is a function in
 $\mathscr {C}^{k,\alpha }(X')$.
$\mathscr {C}^{k,\alpha }(X')$.•
 $\omega _{X'}:= -\mathrm {i} \partial \bar \partial \log (h)|_{X'}$ is a Poincaré type Kähler metric.
$\omega _{X'}:= -\mathrm {i} \partial \bar \partial \log (h)|_{X'}$ is a Poincaré type Kähler metric.
Then we can identify the holomorphic and locally ![]() $L^2$-integrable
$L^2$-integrable ![]() $(n,0)$-forms with values in L:
$(n,0)$-forms with values in L:
Proposition 1. We denote by ![]() $\mathscr {O}_{(2)}(\Omega ^n_{X'}(L|_{X'}),h|_{X'})$ the sheaf of holomorphic L-valued n-forms on
$\mathscr {O}_{(2)}(\Omega ^n_{X'}(L|_{X'}),h|_{X'})$ the sheaf of holomorphic L-valued n-forms on ![]() $X'$, which are locally
$X'$, which are locally ![]() $L^2$ on X with respect to
$L^2$ on X with respect to ![]() $h|_{X'}$. Then
$h|_{X'}$. Then
The proof follows immediately from a Laurent series argument together with the estimates of Poincaré type metrics: sections that are locally square integrable with respect to a metric with a Poincaré type metric extend holomorphically as forms with logarithmic poles to the given snc divisor D (and vice versa).![]() $\Box $
$\Box $
Let ![]() $\mathscr {A}^{n,q}_{(2)}(L|_{X'})$ denote the sheaf on X of L-valued
$\mathscr {A}^{n,q}_{(2)}(L|_{X'})$ denote the sheaf on X of L-valued ![]() $(n,q)$-forms that are locally
$(n,q)$-forms that are locally ![]() $L^2$ integrable with respect to
$L^2$ integrable with respect to ![]() $\omega _{X'}$ and
$\omega _{X'}$ and ![]() $h|_{X'}$ and whose
$h|_{X'}$ and whose ![]() $\overline \partial $-exterior derivatives, taken in the current sense, are also locally
$\overline \partial $-exterior derivatives, taken in the current sense, are also locally ![]() $L^2$. We refer to [Reference Zucker25] or [Reference Brylinski and Zucker5] for more details on the
$L^2$. We refer to [Reference Zucker25] or [Reference Brylinski and Zucker5] for more details on the ![]() $L^2$-complex of sheaves.
$L^2$-complex of sheaves.
Proposition 2. The complex ![]() $(\mathscr {A}^{n,\bullet }_{(2)}(L|_{X'}), \overline \partial )$ of sheaves on X is a fine resolution of
$(\mathscr {A}^{n,\bullet }_{(2)}(L|_{X'}), \overline \partial )$ of sheaves on X is a fine resolution of ![]() $\mathscr {O}_{(2)}(\Omega ^n_{X'}(L|_{X'}),h|_{X'})$. Thus the
$\mathscr {O}_{(2)}(\Omega ^n_{X'}(L|_{X'}),h|_{X'})$. Thus the ![]() $L^2$-Dolbeault cohomology group
$L^2$-Dolbeault cohomology group ![]() $H^0_{(2)}(X', \Omega ^n_{X'}(L|_{X'}))$ can be identified with
$H^0_{(2)}(X', \Omega ^n_{X'}(L|_{X'}))$ can be identified with ![]() $ H^0(X, \Omega ^n(\log D)(L))$, which is of finite dimension.
$ H^0(X, \Omega ^n(\log D)(L))$, which is of finite dimension.
Proof. We decompose the vector bundle locally as a sum of line bundles and apply [Reference Fujiki8, Prop. 2.1]; also compare to [Reference Fujiki8, p.870]. This shows that we have a resolution. The fact that we get a fine resolution is not automatic (compare to [Reference Zucker25, p.175]) because we need cut-off functions with bounded differential. But this holds in the context of Poincaré geometry; see [Reference Zucker24], where it was successfully employed in the one-dimensional case.
3.2 Quasi-coordinates and Hölder spaces
We recall from [Reference Cheng and Yau6] that a quasi-coordinate map is a holomorphic map from an open set ![]() $V \subset \mathbb {C}$ into
$V \subset \mathbb {C}$ into ![]() $X'$ if it is of maximal rank everywhere in V. In this case, V together with the Euclidean coordinates of
$X'$ if it is of maximal rank everywhere in V. In this case, V together with the Euclidean coordinates of ![]() $\mathbb {C}^n$ is called a local quasi-coordinate of
$\mathbb {C}^n$ is called a local quasi-coordinate of ![]() $X'$. According to [Reference Cheng and Yau6, Reference Kobayashi14, Reference Tian, Yau, Yau and Diego21], we have the following:
$X'$. According to [Reference Cheng and Yau6, Reference Kobayashi14, Reference Tian, Yau, Yau and Diego21], we have the following:
Proposition 3. There exists a family ![]() $\mathscr {V}=\{\left (V;v^1,\ldots ,v_n\right )\}$ of local quasi-coordinates of
$\mathscr {V}=\{\left (V;v^1,\ldots ,v_n\right )\}$ of local quasi-coordinates of ![]() $X'$ with the following properties:
$X'$ with the following properties:
(i)
 $X'$ is covered by the images of the quasi-coordinates in
$X'$ is covered by the images of the quasi-coordinates in  $\mathscr {V}$.
$\mathscr {V}$.(ii) The complement of some open neighbourhood of the divisor D in X is covered by the images of finitely many of the quasi-coordinates in
 $\mathscr {V}$, which are local coordinates in the usual sense.
$\mathscr {V}$, which are local coordinates in the usual sense.(iii) For each
 $(V;v^1,\ldots ,v^n) \in \mathscr {V}, v \subset \mathbb {C}^n$ contains an open ball of radius
$(V;v^1,\ldots ,v^n) \in \mathscr {V}, v \subset \mathbb {C}^n$ contains an open ball of radius  $\frac {1}{2}$.
$\frac {1}{2}$.(iv) There are constants
 $c>0$ and
$c>0$ and  $A_k>0, k+0,1,\ldots ,$ such that for every
$A_k>0, k+0,1,\ldots ,$ such that for every  $(V;v^1,\ldots ,v^n) \in \mathscr {V},$ the following inequalities hold:
$(V;v^1,\ldots ,v^n) \in \mathscr {V},$ the following inequalities hold:• We have
as matrices in the sense of positive definiteness. $$ \begin{align*} \frac{1}{c} (\delta_{i\overline{\jmath}}) < (g_{i\overline{\jmath}}) < c (\delta_{i\overline{\jmath}}) \end{align*} $$
$$ \begin{align*} \frac{1}{c} (\delta_{i\overline{\jmath}}) < (g_{i\overline{\jmath}}) < c (\delta_{i\overline{\jmath}}) \end{align*} $$• For any multi-indices
 $I=(i_1,\ldots ,i_p)$ and
$I=(i_1,\ldots ,i_p)$ and  $J=(j_1,\ldots ,j_q)$ of order
$J=(j_1,\ldots ,j_q)$ of order  $|I|=i_1+\ldots + i_p$, respectively
$|I|=i_1+\ldots + i_p$, respectively  $|J|=j_1+\ldots + j_q$, we have where
$|J|=j_1+\ldots + j_q$, we have where $$ \begin{align*} \left| \frac{ \partial^{|I|+|J|} g_{i\overline{\jmath}}}{ \partial v^I \partial \overline{v}^J} \right| < A_{|I|+|J|}, \end{align*} $$
$$ \begin{align*} \left| \frac{ \partial^{|I|+|J|} g_{i\overline{\jmath}}}{ \partial v^I \partial \overline{v}^J} \right| < A_{|I|+|J|}, \end{align*} $$ $ \partial v^{I}=( \partial v^1)^{i_1} \cdots ( \partial v^p)^{i_p}$ and
$ \partial v^{I}=( \partial v^1)^{i_1} \cdots ( \partial v^p)^{i_p}$ and  $ \partial \overline {v}^J=( \partial \overline {v}^1)^{j_1}\cdots ( \partial \overline {v}^q)^{j_q}$.
$ \partial \overline {v}^J=( \partial \overline {v}^1)^{j_1}\cdots ( \partial \overline {v}^q)^{j_q}$.
A complete Kähler manifold ![]() $(X',g)$, which admits a family
$(X',g)$, which admits a family ![]() $\mathscr {V}$ of local quasi-coordinates satisfying the conditions of the proposition, is called being of bounded geometry (of order
$\mathscr {V}$ of local quasi-coordinates satisfying the conditions of the proposition, is called being of bounded geometry (of order ![]() $\infty $).
$\infty $).
Although the coordinate system from Proposition 3 is not a coordinate system in the ordinary sense because of the covering map involved, it makes sense to talk about the components of a tensor field on ![]() $X'$ (or a neighbourhood
$X'$ (or a neighbourhood ![]() $U(p)=(\Delta ^*)^k \times \Delta ^{n-k}$) with respect to these ‘coordinates’
$U(p)=(\Delta ^*)^k \times \Delta ^{n-k}$) with respect to these ‘coordinates’ ![]() $v^i$ by first lifting it to a tensor field
$v^i$ by first lifting it to a tensor field ![]() $\Delta ^n$. The behaviour of the tensor on
$\Delta ^n$. The behaviour of the tensor on ![]() $U(p)$ can thus be examined by looking at the lifted function in a neighbourhood of
$U(p)$ can thus be examined by looking at the lifted function in a neighbourhood of ![]() $(1,\ldots ,1,*,\ldots ,*)$ in
$(1,\ldots ,1,*,\ldots ,*)$ in ![]() $\Delta $.
$\Delta $.
We mention here the transition of tensors from a local coordinate function ![]() $z^i$, where a component
$z^i$, where a component ![]() $D_i$ is given by
$D_i$ is given by ![]() $\{z^i=0\}$ to a quasi-coordinate
$\{z^i=0\}$ to a quasi-coordinate ![]() $v^i$,
$v^i$, ![]() $|v^i|< R <1$, which is given by
$|v^i|< R <1$, which is given by
 $$ \begin{align} \frac{dz^i}{z^i\log|z^i|^2}= \frac{|v^i-1|^2}{(v^i-1)^2}\frac{dv^i}{1-|v^i|^2} \sim dv^i, \end{align} $$
$$ \begin{align} \frac{dz^i}{z^i\log|z^i|^2}= \frac{|v^i-1|^2}{(v^i-1)^2}\frac{dv^i}{1-|v^i|^2} \sim dv^i, \end{align} $$because v is bounded away from ![]() $1$. The respective equation for
$1$. The respective equation for ![]() $\partial /\partial z^1$ reads
$\partial /\partial z^1$ reads
This transformation rule is used to derive estimates from Hölder regular functions and tensors that we will now define. The Hölder spaces ![]() $\mathscr {C}^{k,\alpha }(X')$ are defined in terms of quasi-coordinates for sufficiently large values of k and
$\mathscr {C}^{k,\alpha }(X')$ are defined in terms of quasi-coordinates for sufficiently large values of k and ![]() $0<\alpha <1$. The Hölder norms are computed in terms of the infinite number of quasi-coordinate systems. Following [Reference Cheng and Yau6, Reference Kobayashi14, Reference Tian, Yau, Yau and Diego21], we define
$0<\alpha <1$. The Hölder norms are computed in terms of the infinite number of quasi-coordinate systems. Following [Reference Cheng and Yau6, Reference Kobayashi14, Reference Tian, Yau, Yau and Diego21], we define
Definition 1. Let ![]() $k \in \mathbb {N}_0$ and
$k \in \mathbb {N}_0$ and ![]() $\alpha \in (0,1)$, and denote by
$\alpha \in (0,1)$, and denote by ![]() $C^k(X')$ the space of k-times differentiable functions
$C^k(X')$ the space of k-times differentiable functions ![]() $u: X' \to \mathbb {C}$. For
$u: X' \to \mathbb {C}$. For ![]() $u \in C^k(X')$, let
$u \in C^k(X')$, let
 $$ \begin{align*} \Vert u \rVert_{k,\alpha} = \sup_{(V,v^1,\ldots,v^n) \in \mathscr{V}} \left( \sup _{z \in V} \sum_{|I|+|J|\leq k}{| \partial_v^J\overline{ \partial}_v^J u(z)|} + \sup_{z,z' \in V} \sum_{|I|+|J|=k} \frac{| \partial_v^I\overline{ \partial}_v^J u(z)- \partial_v^I\overline{ \partial}_v^J u(z')|}{|z-z'|^{\alpha}} \right) \end{align*} $$
$$ \begin{align*} \Vert u \rVert_{k,\alpha} = \sup_{(V,v^1,\ldots,v^n) \in \mathscr{V}} \left( \sup _{z \in V} \sum_{|I|+|J|\leq k}{| \partial_v^J\overline{ \partial}_v^J u(z)|} + \sup_{z,z' \in V} \sum_{|I|+|J|=k} \frac{| \partial_v^I\overline{ \partial}_v^J u(z)- \partial_v^I\overline{ \partial}_v^J u(z')|}{|z-z'|^{\alpha}} \right) \end{align*} $$be the ![]() $\mathscr {C}^{k,\alpha }$-norm of u, where
$\mathscr {C}^{k,\alpha }$-norm of u, where ![]() $ \partial _v^I\overline { \partial }_v^J=\frac { \partial ^{|I|+|J|}}{ \partial v^I \partial \overline {v}^J}$. Then let
$ \partial _v^I\overline { \partial }_v^J=\frac { \partial ^{|I|+|J|}}{ \partial v^I \partial \overline {v}^J}$. Then let
be the function space of ![]() $\mathscr {C}^{k,\alpha }$ functions on
$\mathscr {C}^{k,\alpha }$ functions on ![]() $X'$ with respect to
$X'$ with respect to ![]() $\mathscr {V}$.
$\mathscr {V}$.
In a similar way, we can define ![]() $\mathscr {C}^{k,\alpha }$-tensors by pulling back via the quasi-coordinate maps. Exterior derivatives and covariant derivatives of
$\mathscr {C}^{k,\alpha }$-tensors by pulling back via the quasi-coordinate maps. Exterior derivatives and covariant derivatives of ![]() $\mathscr {C}^{k,\alpha }$-tensors are of the same type (with k being replaced by
$\mathscr {C}^{k,\alpha }$-tensors are of the same type (with k being replaced by ![]() $k-1$). The arguments from [Reference Kobayashi14] using Hölder spaces
$k-1$). The arguments from [Reference Kobayashi14] using Hölder spaces ![]() $\mathscr {C}^{k,\alpha }$ (with respect to quasi-coordinates) are valid for all large fixed numbers
$\mathscr {C}^{k,\alpha }$ (with respect to quasi-coordinates) are valid for all large fixed numbers ![]() $k\geq k_0$, where
$k\geq k_0$, where ![]() $k_0$ denotes some minimal degree. During the computations, we will have to take derivatives, products and contractions of such tensors, arriving at
$k_0$ denotes some minimal degree. During the computations, we will have to take derivatives, products and contractions of such tensors, arriving at ![]() $\mathscr {C}^{k,\alpha }$-tensors for some lower value of k. In each of these steps, we will have to increase the lower bound
$\mathscr {C}^{k,\alpha }$-tensors for some lower value of k. In each of these steps, we will have to increase the lower bound ![]() $k_0$. Only finitely many such steps will be necessary. We will increase
$k_0$. Only finitely many such steps will be necessary. We will increase ![]() $k_0$ tacitly.
$k_0$ tacitly.
Let ![]() $\omega _{X'}$ be the complete Poincaré type Kähler form from the previous section.
$\omega _{X'}$ be the complete Poincaré type Kähler form from the previous section.
Lemma 3.1. Any ![]() $\mathscr {C}^{k,\alpha }$-tensor on
$\mathscr {C}^{k,\alpha }$-tensor on ![]() $X'$ is globally square-integrable.
$X'$ is globally square-integrable.
The proof follows immediately from the given uniform bounds of such tensors in terms of the above quasi-coordinate systems and the metric ![]() $\omega _{X'}$ with respect to the transition equations of the type in equation (3.1): take the pointwise norm of such a tensor with respect to the given metric. We consider the resulting function a bounded
$\omega _{X'}$ with respect to the transition equations of the type in equation (3.1): take the pointwise norm of such a tensor with respect to the given metric. We consider the resulting function a bounded ![]() $\mathscr {C}^{k,\alpha }$-tensor (for some value of k), which means it is uniformly bounded in terms of quasi-coordinate systems (or any other coordinate systems). Finally, we use the boundedness of the volume of
$\mathscr {C}^{k,\alpha }$-tensor (for some value of k), which means it is uniformly bounded in terms of quasi-coordinate systems (or any other coordinate systems). Finally, we use the boundedness of the volume of ![]() $X'$.
$X'$. ![]() $\Box $
$\Box $
3.3 Hodge theory on the open fibres
In this section, we summarise the Hodge theory on the complete, noncompact Kähler manifold ![]() $(X',\omega _{X'})$, for which we refer to the book of Marinescu and Ma [Reference Ma and Marinescu16, Chapter 3]. We consider the holomorphic vector bundle
$(X',\omega _{X'})$, for which we refer to the book of Marinescu and Ma [Reference Ma and Marinescu16, Chapter 3]. We consider the holomorphic vector bundle ![]() $E=K_{X'}\otimes L|_{X'}$ equipped with the hermitian metric
$E=K_{X'}\otimes L|_{X'}$ equipped with the hermitian metric ![]() $h|_{X'}$.
$h|_{X'}$.
For the operator ![]() $\bar \partial $ defined on the smooth, compactly supported forms
$\bar \partial $ defined on the smooth, compactly supported forms ![]() $A_0^{0,q}(X',E) \subset L^{0,q}_{(2)}(X',E)$, we consider its formal adjoint
$A_0^{0,q}(X',E) \subset L^{0,q}_{(2)}(X',E)$, we consider its formal adjoint ![]() $\bar \partial ^*$. For
$\bar \partial ^*$. For ![]() $s_1 \in L_{(2)}^{0,q}(X',E)$, we can calculate
$s_1 \in L_{(2)}^{0,q}(X',E)$, we can calculate ![]() $\bar \partial s_1$ in the sense of currents:
$\bar \partial s_1$ in the sense of currents: ![]() $\bar \partial s_1$ is the current defined by
$\bar \partial s_1$ is the current defined by
Then we have
Lemma 3.2 [Reference Ma and Marinescu16, Lemma 3.1.1].
The operator ![]() $\bar \partial _{\max }$ defined by
$\bar \partial _{\max }$ defined by
 $$ \begin{align*} &\operatorname{Dom} (\bar \partial_{\max}) = \{s \in L_{(2)}^{0,q}(X',E)\; : \; \bar \partial s \in L_{(2)}^{0,q+1}(X',E)\}\\ & \bar \partial_{\max} s = \bar \partial s \quad \mbox{ for } s \in \operatorname{Dom}(\bar \partial_{\max}) \end{align*} $$
$$ \begin{align*} &\operatorname{Dom} (\bar \partial_{\max}) = \{s \in L_{(2)}^{0,q}(X',E)\; : \; \bar \partial s \in L_{(2)}^{0,q+1}(X',E)\}\\ & \bar \partial_{\max} s = \bar \partial s \quad \mbox{ for } s \in \operatorname{Dom}(\bar \partial_{\max}) \end{align*} $$is a densely defined, closed extension called the maximal extension of ![]() $\bar \partial .$
$\bar \partial .$
In the sequel, we work with the maximal extension and simply write ![]() $\bar \partial = \bar \partial _{\max }$. The Hilbert space adjoint of
$\bar \partial = \bar \partial _{\max }$. The Hilbert space adjoint of ![]() $\bar \partial _{\max }$ is denoted by
$\bar \partial _{\max }$ is denoted by ![]() $\bar \partial ^*_H$. We note that
$\bar \partial ^*_H$. We note that ![]() $\bar \partial ^*_H \subset (\bar \partial ^*)_H$ and
$\bar \partial ^*_H \subset (\bar \partial ^*)_H$ and ![]() $\bar \partial _{\max } = (\bar \partial ^*_H)^*_H$. From now on, we work with
$\bar \partial _{\max } = (\bar \partial ^*_H)^*_H$. From now on, we work with ![]() $\bar \partial ^*_H$ and just write
$\bar \partial ^*_H$ and just write ![]() $\bar \partial ^*$.
$\bar \partial ^*$.
The Laplacian ![]() $\Box =\bar \partial \bar \partial ^*+\bar \partial ^*\bar \partial $ is a densely defined, positive operator, so one can consider its Friedrichs extension. But in the context of
$\Box =\bar \partial \bar \partial ^*+\bar \partial ^*\bar \partial $ is a densely defined, positive operator, so one can consider its Friedrichs extension. But in the context of ![]() $L^2$ cohomology, it is useful to consider another extension:
$L^2$ cohomology, it is useful to consider another extension:
Proposition 4 [Reference Ma and Marinescu16, Proposition 3.1.2].
The operator defined by
 $$ \begin{align*} & \operatorname{Dom} (\Box) = \{s \in \operatorname{Dom}(\bar \partial) \cap \operatorname{Dom}(\bar \partial^*)\; : \; \bar \partial s \in \operatorname{Dom}(\bar \partial^*), \; \bar \partial^* s \in \operatorname{Dom}(\bar \partial)\},\\ & \Box s = \bar \partial^* \bar \partial s + \bar \partial \bar \partial^* s \quad \mbox{ for } s \in \operatorname{Dom}(\Box) \end{align*} $$
$$ \begin{align*} & \operatorname{Dom} (\Box) = \{s \in \operatorname{Dom}(\bar \partial) \cap \operatorname{Dom}(\bar \partial^*)\; : \; \bar \partial s \in \operatorname{Dom}(\bar \partial^*), \; \bar \partial^* s \in \operatorname{Dom}(\bar \partial)\},\\ & \Box s = \bar \partial^* \bar \partial s + \bar \partial \bar \partial^* s \quad \mbox{ for } s \in \operatorname{Dom}(\Box) \end{align*} $$is a positive self-adjoint extension of the Laplacian, called the Gaffney extension.
We note that this result relies on Gaffney’s generalisation of Stokes’ theorem that we will use tacitly during our computation:
Proposition 5 [Reference Gaffney9].
Let ![]() $(M,g)$ be an orientable complete Riemannian manifold of real dimension
$(M,g)$ be an orientable complete Riemannian manifold of real dimension ![]() $2n$ whose Riemann tensor is of class
$2n$ whose Riemann tensor is of class ![]() $C^2$. Let
$C^2$. Let ![]() $\gamma $ be a
$\gamma $ be a ![]() $(2n-1)$-form on M of class
$(2n-1)$-form on M of class ![]() $C^1$ such that both
$C^1$ such that both ![]() $\gamma $ and
$\gamma $ and ![]() $d \gamma $ are in
$d \gamma $ are in ![]() $L^1$. Then
$L^1$. Then
We define the space of harmonic forms ![]() $\mathscr {H}^{0,q}(X',E) \subset L_{(2)}^{0,q}(X',E)$ by
$\mathscr {H}^{0,q}(X',E) \subset L_{(2)}^{0,q}(X',E)$ by
We see that
The qth ![]() $L^2$ Dolbeault cohomology is defined by
$L^2$ Dolbeault cohomology is defined by
which is of course the same as the group ![]() $H^q_{(2)}(X',K_{X'}^p(L|_{X'}))$ from Proposition 2, because the
$H^q_{(2)}(X',K_{X'}^p(L|_{X'}))$ from Proposition 2, because the ![]() $L^2$-cohomology can be also computed by smooth forms. From this, we also get
$L^2$-cohomology can be also computed by smooth forms. From this, we also get
Proposition 6. The ![]() $L^2$-Dolbeault cohomology
$L^2$-Dolbeault cohomology ![]() $H^{0,q}_{(2)}(X',E) $ is finite-dimensional, and we have
$H^{0,q}_{(2)}(X',E) $ is finite-dimensional, and we have
Moreover, the images of ![]() $\bar \partial $ and
$\bar \partial $ and ![]() $\bar \partial ^*$ are closed in
$\bar \partial ^*$ are closed in ![]() $L_{(2)}(X',E)$, and thus there exists a constant
$L_{(2)}(X',E)$, and thus there exists a constant ![]() $C>0$ such that
$C>0$ such that
for all ![]() $s \in \operatorname {Dom}(\bar \partial ) \cap \operatorname {Dom}{\bar \partial ^*}\cap L^{0,q}_{(2)}(X',E), \,s \perp \mathscr {H}^{0,q}(X',E)$.
$s \in \operatorname {Dom}(\bar \partial ) \cap \operatorname {Dom}{\bar \partial ^*}\cap L^{0,q}_{(2)}(X',E), \,s \perp \mathscr {H}^{0,q}(X',E)$.
Proof. By Proposition 2, we know that we can identify the ![]() $L^2$-Dolbeault cohomology with the sheaf cohomology of the locally free sheaf
$L^2$-Dolbeault cohomology with the sheaf cohomology of the locally free sheaf ![]() $\Omega ^p(\log D) \otimes K_X$ on the compactification X; hence it must be finite-dimensional. This immediately implies that the images of
$\Omega ^p(\log D) \otimes K_X$ on the compactification X; hence it must be finite-dimensional. This immediately implies that the images of ![]() $\bar \partial $ (and hence also of
$\bar \partial $ (and hence also of ![]() $\bar \partial ^*$) are closed ([Reference Brylinski and Zucker5, Proposition 3.5]) and the isomorphism with the space of harmonic forms ([Reference Brylinski and Zucker5, Corollary 3.6]). The stated estimate for the
$\bar \partial ^*$) are closed ([Reference Brylinski and Zucker5, Proposition 3.5]) and the isomorphism with the space of harmonic forms ([Reference Brylinski and Zucker5, Corollary 3.6]). The stated estimate for the ![]() $L^2$-norm for a section s that is orthogonal to the space of harmonic forms follows from the closedness of
$L^2$-norm for a section s that is orthogonal to the space of harmonic forms follows from the closedness of ![]() $\operatorname {Im}(\bar \partial )$ and
$\operatorname {Im}(\bar \partial )$ and ![]() $\operatorname {Im}(\bar \partial ^*)$ ([Reference Ma and Marinescu16, Prop. 3.1.6]).
$\operatorname {Im}(\bar \partial ^*)$ ([Reference Ma and Marinescu16, Prop. 3.1.6]).
Corollary 3. We have the strong Hodge decomposition, which is orthogonal:
 $$ \begin{align*} L^{0,q}_{(2)}(X',E) &= \mathscr{H}^{0,q}(X',E) \oplus \operatorname{Im}(\Box) = \mathscr{H}^{0,q}(X',E) \oplus \operatorname{Im}(\bar \partial\bar \partial^*) \oplus \operatorname{Im}(\bar \partial^*\bar \partial),\\ \operatorname{Ker}(\bar \partial) \cap L^{0,q}_{(2)}(X',E) &= \mathscr{H}^{0,q}(X',E) \oplus \left( \operatorname{Im}(\bar \partial) \cap L^{0,q}_{(2)}(X',E) \right). \end{align*} $$
$$ \begin{align*} L^{0,q}_{(2)}(X',E) &= \mathscr{H}^{0,q}(X',E) \oplus \operatorname{Im}(\Box) = \mathscr{H}^{0,q}(X',E) \oplus \operatorname{Im}(\bar \partial\bar \partial^*) \oplus \operatorname{Im}(\bar \partial^*\bar \partial),\\ \operatorname{Ker}(\bar \partial) \cap L^{0,q}_{(2)}(X',E) &= \mathscr{H}^{0,q}(X',E) \oplus \left( \operatorname{Im}(\bar \partial) \cap L^{0,q}_{(2)}(X',E) \right). \end{align*} $$Moreover, there exists a bounded operator G on ![]() $L^{0,q}_{(2)}(X',E)$, called the Green operator, such that
$L^{0,q}_{(2)}(X',E)$, called the Green operator, such that
where H is the orthogonal projection form ![]() $L^{0,q}_{(2)}(X',E)$ onto
$L^{0,q}_{(2)}(X',E)$ onto ![]() $\mathscr {H}^{0,q}(X',E)$.
$\mathscr {H}^{0,q}(X',E)$.
Proof. See [Reference Ma and Marinescu16, Theorem 3.1.8].
Remark 3.3. By the usual elliptic regularity theory, we get that harmonic sections are in fact smooth. G maps smooth forms to smooth forms so that we can cut down the Hodge decomposition to the space of smooth ![]() $L^2$ sections:
$L^2$ sections:
3.4 Families of logarithmic pairs
Let ![]() $(\mathscr {X},\mathscr {D})$ be a smooth log pair: that is,
$(\mathscr {X},\mathscr {D})$ be a smooth log pair: that is, ![]() $\mathscr {X}$ a complex manifold and
$\mathscr {X}$ a complex manifold and ![]() $\mathscr {D} \subset \mathscr {X}$ a reduced snc divisor. The boundary divisor
$\mathscr {D} \subset \mathscr {X}$ a reduced snc divisor. The boundary divisor ![]() $\mathscr {D}$ is written as a sum of its irreducible components
$\mathscr {D}$ is written as a sum of its irreducible components ![]() $\mathscr {D} = \mathcal {D}_1+\ldots + \mathscr {D}_k$. If
$\mathscr {D} = \mathcal {D}_1+\ldots + \mathscr {D}_k$. If ![]() $I \subset \{1,\ldots ,k\}$ is any non-empty subset, we consider the intersection
$I \subset \{1,\ldots ,k\}$ is any non-empty subset, we consider the intersection ![]() $\mathscr {D}_I:=\cap _{i \in I}\mathscr {D}_i$.
$\mathscr {D}_I:=\cap _{i \in I}\mathscr {D}_i$.
Definition 2 [Reference Kebekus13, Def. 3.4].
For a smooth log pair ![]() $(\mathscr {X},\mathscr {D})$ and a proper holomorphic submersion
$(\mathscr {X},\mathscr {D})$ and a proper holomorphic submersion ![]() $f: \mathscr {X} \to S$, we say that
$f: \mathscr {X} \to S$, we say that ![]() $\mathscr {D}$ is relatively snc or that f is a snc morphism if for any set I with
$\mathscr {D}$ is relatively snc or that f is a snc morphism if for any set I with ![]() $D_I \neq \emptyset $, all the restricted morphisms
$D_I \neq \emptyset $, all the restricted morphisms ![]() $f|_{\mathscr {D}_I}\to S$ are also smooth of relative dimension
$f|_{\mathscr {D}_I}\to S$ are also smooth of relative dimension ![]() $\dim \mathscr {X} - \dim S-|I|$.
$\dim \mathscr {X} - \dim S-|I|$.
If ![]() $s \in S$ is any point, set
$s \in S$ is any point, set ![]() $X_s=f^{-1}(s)$ and
$X_s=f^{-1}(s)$ and ![]() $D_s:= \mathscr {D} \cap X_s$. Then
$D_s:= \mathscr {D} \cap X_s$. Then ![]() $X_s$ is smooth and
$X_s$ is smooth and ![]() $(X_s,D_s)$ is a snc pair. Moreover, the number of irreducible components of
$(X_s,D_s)$ is a snc pair. Moreover, the number of irreducible components of ![]() $D_s$ is also k, which is the number of irreducible components of
$D_s$ is also k, which is the number of irreducible components of ![]() $\mathscr {D}$. This excludes phenomena like the deformation of the smooth hyperbola
$\mathscr {D}$. This excludes phenomena like the deformation of the smooth hyperbola ![]() $\{wz=s \neq 0\}$ into the snc divisor
$\{wz=s \neq 0\}$ into the snc divisor ![]() $\{zw=0\}$ that has two components. The reason for this will become clear later. Moreover, the definition implies
$\{zw=0\}$ that has two components. The reason for this will become clear later. Moreover, the definition implies
Lemma 3.4. For a smooth log pair ![]() $(\mathscr {X},\mathscr {D})$ and a smooth snc morphism
$(\mathscr {X},\mathscr {D})$ and a smooth snc morphism ![]() $f:\mathscr {X} \to S$, we can find (after shrinking S to a contractible neighbourhood) a differentiable trivialisation
$f:\mathscr {X} \to S$, we can find (after shrinking S to a contractible neighbourhood) a differentiable trivialisation ![]() $\Phi : \mathscr {X} \xrightarrow {\sim } X \times S$ such that the restriction
$\Phi : \mathscr {X} \xrightarrow {\sim } X \times S$ such that the restriction ![]() $\Phi |_{\mathscr {D}}:\mathscr {D} \xrightarrow {\sim }\ D \times S$ is also a smooth trivialisation.
$\Phi |_{\mathscr {D}}:\mathscr {D} \xrightarrow {\sim }\ D \times S$ is also a smooth trivialisation.
The lemma says that we can trivialise the pair ![]() $(X_s,D_s)$ in a differentiable way. By restriction to
$(X_s,D_s)$ in a differentiable way. By restriction to ![]() $\mathscr {X}':=\mathscr {X}\setminus \mathscr {D}$, we find a smooth trivialisation of
$\mathscr {X}':=\mathscr {X}\setminus \mathscr {D}$, we find a smooth trivialisation of ![]() $\mathscr {X}'\cong X'\times S$.
$\mathscr {X}'\cong X'\times S$.
Given a smooth log pair ![]() $(X,D)$ and a point x, there exists an open neighbourhood
$(X,D)$ and a point x, there exists an open neighbourhood ![]() $U=U(x)$ and holomorphic coordinates
$U=U(x)$ and holomorphic coordinates ![]() $z_1, \dots ,z_n$ such that
$z_1, \dots ,z_n$ such that ![]() $D\cap U=\{z_1\cdots z_r\}$ for some
$D\cap U=\{z_1\cdots z_r\}$ for some ![]() $0\leq r \leq n$. The following is the relative analogue of this fact:
$0\leq r \leq n$. The following is the relative analogue of this fact:
Lemma 3.5 [Reference Kebekus13, Lemma 3.7].
Let ![]() $(\mathscr {X},\mathscr {D})$ be a smooth snc pair and
$(\mathscr {X},\mathscr {D})$ be a smooth snc pair and ![]() $f: \mathscr {X} \to S$ an snc morphism. For any point
$f: \mathscr {X} \to S$ an snc morphism. For any point ![]() $x \in \mathscr {X}$, there exist open neighbourhoods
$x \in \mathscr {X}$, there exist open neighbourhoods ![]() $V=V(f(x))\subset S$ and
$V=V(f(x))\subset S$ and ![]() $U=U(x) \subset f^{-1}(V) \subset \mathscr {X}$ and holomorphic coordinates
$U=U(x) \subset f^{-1}(V) \subset \mathscr {X}$ and holomorphic coordinates ![]() $z_1,\dots , z_n, z_{n+1},\dots , z_{n+m}$ around x and
$z_1,\dots , z_n, z_{n+1},\dots , z_{n+m}$ around x and ![]() $s_1,\dots ,s_m$ around
$s_1,\dots ,s_m$ around ![]() $f(x)$ and a number
$f(x)$ and a number ![]() $0\leq r\leq n$ such that the following hold:
$0\leq r\leq n$ such that the following hold:
(i) We have
 $z_{n+i}=s_i \circ f$ for all indices
$z_{n+i}=s_i \circ f$ for all indices  $1\le i\leq m$.
$1\le i\leq m$.(ii)
 $\mathscr {D} \cap \mathscr {X}=\{z_{1}\cdots z_r=0\}$.
$\mathscr {D} \cap \mathscr {X}=\{z_{1}\cdots z_r=0\}$.
In the following, we will make use of these adapted coordinates tacitly. In the applications, we also consider the following families:
Definition 3. A holomorphic family of log-canonically polarised pairs consists of a smooth snc pair ![]() $(\mathscr {X},\mathscr {D})$ and a snc morphism
$(\mathscr {X},\mathscr {D})$ and a snc morphism ![]() $f:\mathscr {X} \to S$ such that
$f:\mathscr {X} \to S$ such that ![]() $K_{X_s}+D_s$ is ample for each
$K_{X_s}+D_s$ is ample for each ![]() $s \in S$.
$s \in S$.
In particular, our families are logarithmic deformations in the sense of [Reference Kawamata12] and generalise the deformations considered in [Reference Schumacher18] to the case of singular snc divisors.
Remark 3.6. By the ![]() $C^{\infty }$ trivialisation
$C^{\infty }$ trivialisation ![]() $\mathscr {X}'\cong X'\times S$ and the fact that nearby fibres
$\mathscr {X}'\cong X'\times S$ and the fact that nearby fibres ![]() $(X_s,g_s)$ and bundles
$(X_s,g_s)$ and bundles ![]() $E^{\prime }_s=K_{X^{\prime }_s}\otimes L|_{X^{\prime }_s}$ are quasi-isometric implies that the
$E^{\prime }_s=K_{X^{\prime }_s}\otimes L|_{X^{\prime }_s}$ are quasi-isometric implies that the ![]() $L^2$-spaces
$L^2$-spaces ![]() $L^{0,q}_{(2)}(X^{\prime }_s,E^{\prime }_s)$ and the domain of the Laplacians
$L^{0,q}_{(2)}(X^{\prime }_s,E^{\prime }_s)$ and the domain of the Laplacians ![]() $\operatorname {Dom}(\Box _s)$ do not depend on the fibre
$\operatorname {Dom}(\Box _s)$ do not depend on the fibre ![]() $X^{\prime }_s.$ The same holds for the Hölder spaces
$X^{\prime }_s.$ The same holds for the Hölder spaces ![]() $\mathscr {C}^{k,\alpha }(X^{\prime }_s)$.
$\mathscr {C}^{k,\alpha }(X^{\prime }_s)$.
3.5 L 2-integrable Kodaira-Spencer forms
We consider a holomorphic family of smooth log pairs ![]() $\mathscr {D} \overset {i}{\hookrightarrow } \mathscr {X} \overset {f}{\rightarrow } S$ and a hermitian holomorphic line bundle
$\mathscr {D} \overset {i}{\hookrightarrow } \mathscr {X} \overset {f}{\rightarrow } S$ and a hermitian holomorphic line bundle ![]() $(\mathscr {L},h)$ on
$(\mathscr {L},h)$ on ![]() $\mathscr {X}$ whose inverse metric has Poincaré type singularities along
$\mathscr {X}$ whose inverse metric has Poincaré type singularities along ![]() $\mathscr {D}$, as already described in the introduction. Moreover, we recall that we have defined on
$\mathscr {D}$, as already described in the introduction. Moreover, we recall that we have defined on ![]() $\mathscr {X}'$ the global
$\mathscr {X}'$ the global ![]() $(1,1)$-form
$(1,1)$-form
 $$ \begin{align*} \omega_{\mathscr{X}'} = -\mathrm{i}\partial\overline\partial (\log h)= \mathrm{i} \partial \bar \partial \log(h^{C^{\infty}}_{\mathscr{L}^{-1}})-\sum_{i=1}^l{\mathrm{i} \partial \bar \partial\log(||\sigma_i||^2 \log^2||\sigma_i||^2})+\mathrm{i} \partial \bar \partial u, \end{align*} $$
$$ \begin{align*} \omega_{\mathscr{X}'} = -\mathrm{i}\partial\overline\partial (\log h)= \mathrm{i} \partial \bar \partial \log(h^{C^{\infty}}_{\mathscr{L}^{-1}})-\sum_{i=1}^l{\mathrm{i} \partial \bar \partial\log(||\sigma_i||^2 \log^2||\sigma_i||^2})+\mathrm{i} \partial \bar \partial u, \end{align*} $$whose restrictions to the open fibres ![]() $X^{\prime }_s$ give a smooth family of Poincaré type Kähler forms
$X^{\prime }_s$ give a smooth family of Poincaré type Kähler forms ![]() $\omega _s = \omega _{\mathscr {X}'}|_{X^{\prime }_s}$.
$\omega _s = \omega _{\mathscr {X}'}|_{X^{\prime }_s}$.
By using the local description
with respect to the local coordinates ![]() $(z,s)$, we can say that the restrictions of
$(z,s)$, we can say that the restrictions of ![]() $ \omega _{\mathscr {X}'}$ as well as restrictions of contractions depend in a
$ \omega _{\mathscr {X}'}$ as well as restrictions of contractions depend in a ![]() $C^{\infty }$ way upon the parameter.
$C^{\infty }$ way upon the parameter.
Lemma 3.7. The restrictions
 $$ \begin{align*} \omega_{\mathscr{X}'}\llcorner (\partial/\partial s^i)|X^{\prime}_s &= g_{i\overline\beta}dz^{\overline\beta}|X^{\prime}_s\\ \omega_{\mathscr{X}'}\llcorner (\partial/\partial s^{\overline \jmath})|X^{\prime}_s &= g_{\alpha\overline \jmath}dz^{\alpha}|X^{\prime}_s\\ \omega_{\mathscr{X}'}\llcorner (\partial/\partial s^i\wedge ds^{\overline\jmath})|X^{\prime}_s&= g_{i\overline \jmath}|X^{\prime}_s \end{align*} $$
$$ \begin{align*} \omega_{\mathscr{X}'}\llcorner (\partial/\partial s^i)|X^{\prime}_s &= g_{i\overline\beta}dz^{\overline\beta}|X^{\prime}_s\\ \omega_{\mathscr{X}'}\llcorner (\partial/\partial s^{\overline \jmath})|X^{\prime}_s &= g_{\alpha\overline \jmath}dz^{\alpha}|X^{\prime}_s\\ \omega_{\mathscr{X}'}\llcorner (\partial/\partial s^i\wedge ds^{\overline\jmath})|X^{\prime}_s&= g_{i\overline \jmath}|X^{\prime}_s \end{align*} $$are ![]() $\mathscr {C}^{k,\alpha }$-tensors that depend in a
$\mathscr {C}^{k,\alpha }$-tensors that depend in a ![]() $C^{\infty }$ way upon the parameter
$C^{\infty }$ way upon the parameter ![]() $s\in S$. In particular, they are smooth and
$s\in S$. In particular, they are smooth and ![]() $L^2$ integrable tensors
$L^2$ integrable tensors ![]() $(\mathscr {A}_{(2)}$-tensors for short). The analogous statement holds if
$(\mathscr {A}_{(2)}$-tensors for short). The analogous statement holds if ![]() $\omega _{\mathscr {X}'}$ is replaced by
$\omega _{\mathscr {X}'}$ is replaced by ![]() $\widetilde \omega _{\mathscr {X}'}$, where the first two tensors do not change.
$\widetilde \omega _{\mathscr {X}'}$, where the first two tensors do not change.
Proof. The only critical term appearing in the expression of ![]() $\omega _{\mathscr {X}'}$ is the one coming from u. The purely vertical components are dealt with the fact that
$\omega _{\mathscr {X}'}$ is the one coming from u. The purely vertical components are dealt with the fact that ![]() $u|_{X^{\prime }_s}$ lies in
$u|_{X^{\prime }_s}$ lies in ![]() $\in \mathscr {C}^{k,\alpha }$. But now, by assumption, the map
$\in \mathscr {C}^{k,\alpha }$. But now, by assumption, the map ![]() $s \mapsto u(z,s) \in \mathscr {C}^{k,\alpha }$ is Fréchet differentiable, so that the (locally defined) partial derivatives in the base direction of the function u are again of class
$s \mapsto u(z,s) \in \mathscr {C}^{k,\alpha }$ is Fréchet differentiable, so that the (locally defined) partial derivatives in the base direction of the function u are again of class ![]() $\mathscr {C}^{k,\alpha }$.
$\mathscr {C}^{k,\alpha }$.
Horizontal lifts of tangent vectors from S to the total space ![]() $\mathscr {X}'$ are defined as perpendicular to the fibres of
$\mathscr {X}'$ are defined as perpendicular to the fibres of ![]() $\mathscr {X}' \to S$ with respect to
$\mathscr {X}' \to S$ with respect to ![]() $\omega _{\mathscr {X}'}$. Here we only need the property that the restrictions of
$\omega _{\mathscr {X}'}$. Here we only need the property that the restrictions of ![]() $\omega _{\mathscr {X}'}$ to the fibres are positive definite.
$\omega _{\mathscr {X}'}$ to the fibres are positive definite.
We denote by ![]() $(g^{\overline \beta \alpha })$ the inverses of the metric tensors
$(g^{\overline \beta \alpha })$ the inverses of the metric tensors ![]() $g_{\alpha \overline \beta }$ of
$g_{\alpha \overline \beta }$ of ![]() $\omega _s$ on the fibres
$\omega _s$ on the fibres ![]() $X^{\prime }_s$. Covariant derivatives are always taken with respect to these metrics. We will use both the semicolon notation and the
$X^{\prime }_s$. Covariant derivatives are always taken with respect to these metrics. We will use both the semicolon notation and the ![]() $\nabla $-notation. We continue using Greek indices for tensors in fibre direction and
$\nabla $-notation. We continue using Greek indices for tensors in fibre direction and ![]() $\partial _{\alpha } = \partial /\partial z^{\alpha }$.
$\partial _{\alpha } = \partial /\partial z^{\alpha }$.
The horizontal lift ![]() $v_i$ of a tangent vector
$v_i$ of a tangent vector ![]() $ \partial _i={\partial }/{\partial } s^i$ is a differentiable lift of
$ \partial _i={\partial }/{\partial } s^i$ is a differentiable lift of ![]() $ \partial _i$ to
$ \partial _i$ to ![]() $\mathscr {X}'$, which is orthogonal to the fibres with respect to the sesquilinear form
$\mathscr {X}'$, which is orthogonal to the fibres with respect to the sesquilinear form ![]() $\omega _{\mathscr {X}'}$:
$\omega _{\mathscr {X}'}$:
This is well defined since the form ![]() $\omega _{\mathscr {X}'}$ is positive when restricted to the fibres. In terms of the coefficients of
$\omega _{\mathscr {X}'}$ is positive when restricted to the fibres. In terms of the coefficients of ![]() $\omega _{\mathscr {X}}$, it is given by
$\omega _{\mathscr {X}}$, it is given by
where
Lemma 3.8. Let ![]() $A_i = \overline \partial v_i|X^{\prime }_s$: that is,
$A_i = \overline \partial v_i|X^{\prime }_s$: that is,
Then ![]() $A_i$ is of class
$A_i$ is of class ![]() $\mathscr {C}^{k,\alpha }$ and satisfies
$\mathscr {C}^{k,\alpha }$ and satisfies ![]() $\overline \partial A_i=0$. In particular, it lies in
$\overline \partial A_i=0$. In particular, it lies in ![]() $A^{0,1}_{(2)}(X^{\prime }_s,T_{X^{\prime }_s})$.
$A^{0,1}_{(2)}(X^{\prime }_s,T_{X^{\prime }_s})$.
The proof is the same as in [Reference Schumacher18, Lemma 3].![]() $\Box $
$\Box $
The Kodaira-Spencer map for a family ![]() $\mathscr {D} \overset {i}{\hookrightarrow } \mathscr {X} \overset {f}{\rightarrow } S$
$\mathscr {D} \overset {i}{\hookrightarrow } \mathscr {X} \overset {f}{\rightarrow } S$
was already defined in [Reference Schumacher18]. Analogous results like those of Section 3.1 hold for the sheaf of holomorphic vector fields:
The sequence ![]() $(\mathscr {A}^{0,\bullet }_{(2)}(\mathcal {T}_{X^{\prime }_s}),\overline {{\partial }})$ is a fine resolution of the sheaf of
$(\mathscr {A}^{0,\bullet }_{(2)}(\mathcal {T}_{X^{\prime }_s}),\overline {{\partial }})$ is a fine resolution of the sheaf of ![]() $L^2$ holomorphic vector fields
$L^2$ holomorphic vector fields ![]() $\mathscr {O}_{(2)}(T_{X^{\prime }_s})$, which is isomorphic to
$\mathscr {O}_{(2)}(T_{X^{\prime }_s})$, which is isomorphic to ![]() $T_{X_s}(-\log D_s):=(\Omega ^1_{X_s}(\log D_s))^{\vee }$.
$T_{X_s}(-\log D_s):=(\Omega ^1_{X_s}(\log D_s))^{\vee }$.
In particular,
and the above explicit construction yields a ![]() $L^2$-Dolbeault representative
$L^2$-Dolbeault representative ![]() $A^{\alpha }_{i\overline {\beta }}{\partial }_{\alpha } dz^{\overline {\beta }}$ of
$A^{\alpha }_{i\overline {\beta }}{\partial }_{\alpha } dz^{\overline {\beta }}$ of ![]() $\rho _s({\partial }/{\partial } s^i)$, where the Kodaira-Spencer map is taken as map
$\rho _s({\partial }/{\partial } s^i)$, where the Kodaira-Spencer map is taken as map
We will also need the following fact that follows from the definition.
Lemma 3.9. Let ![]() $A_i^{\alpha \sigma }=g^{\overline {\beta } \sigma }A_{i\overline {\beta }}^{\alpha }$. Then
$A_i^{\alpha \sigma }=g^{\overline {\beta } \sigma }A_{i\overline {\beta }}^{\alpha }$. Then
Finally, the pointwise inner product with respect to ![]() $\omega _{\mathscr {X}'}$ of two horizontal lifts
$\omega _{\mathscr {X}'}$ of two horizontal lifts
called the geodesic curvature, has an expression
so that we conclude from Lemma 3.7 that this function lies in ![]() $\mathscr {C}^{k,\alpha }$.
$\mathscr {C}^{k,\alpha }$.
3.6 Bundles of L 2-integrable forms
Now we consider the ![]() $L^2$ condition on the total space
$L^2$ condition on the total space ![]() $\mathscr {X}$. Because the form
$\mathscr {X}$. Because the form ![]() $\omega _{\mathscr {X}'}$ is fibrewise positive, for any
$\omega _{\mathscr {X}'}$ is fibrewise positive, for any ![]() $s_0\in S$ after replacing S by a neighbourhood (contractible and Stein), there exists a positive hermitian form
$s_0\in S$ after replacing S by a neighbourhood (contractible and Stein), there exists a positive hermitian form ![]() $\omega _S$ such that
$\omega _S$ such that ![]() $\widetilde {\omega }^{\prime }_{\mathscr {X}} = \omega _{\mathscr {X}'}+f^*\omega _S$ is a positive form on
$\widetilde {\omega }^{\prime }_{\mathscr {X}} = \omega _{\mathscr {X}'}+f^*\omega _S$ is a positive form on ![]() $\mathscr {X}'$.
$\mathscr {X}'$.
The previous arguments imply that the statements of Proposition 1 and Proposition 2 hold for the total spaces ![]() $(\mathscr {X}',\widetilde \omega _{\mathscr {X}'})$. The sheaves of locally
$(\mathscr {X}',\widetilde \omega _{\mathscr {X}'})$. The sheaves of locally ![]() $L^2$ sections
$L^2$ sections ![]() $\mathscr {O}_{(2)}(\Omega ^n_{\mathscr {X}'}(\mathscr {L}|_{\mathscr {X}'}), \widetilde \omega _{\mathscr {X}'},h|_{\mathscr {X}'})$ on the whole total space
$\mathscr {O}_{(2)}(\Omega ^n_{\mathscr {X}'}(\mathscr {L}|_{\mathscr {X}'}), \widetilde \omega _{\mathscr {X}'},h|_{\mathscr {X}'})$ on the whole total space ![]() $\mathscr {X}$ are equal to
$\mathscr {X}$ are equal to ![]() $\Omega ^n_{\mathscr {X}}(\log \mathscr {D})(\mathscr {L})$, and an analogous fine resolution in terms of square-integrable forms exists. However, the sheaves
$\Omega ^n_{\mathscr {X}}(\log \mathscr {D})(\mathscr {L})$, and an analogous fine resolution in terms of square-integrable forms exists. However, the sheaves ![]() $\Omega ^n_{\mathscr {X}}(\log \mathcal {D})$ of log n-forms on the total space
$\Omega ^n_{\mathscr {X}}(\log \mathcal {D})$ of log n-forms on the total space ![]() $\mathscr {X}$ are not suitable for our methods.
$\mathscr {X}$ are not suitable for our methods.
Instead, we will need the coherent sheaf ![]() $\Omega ^n(\log \mathcal {D})_{\mathscr {X}/S}(\mathscr {L})$ and the sheaves
$\Omega ^n(\log \mathcal {D})_{\mathscr {X}/S}(\mathscr {L})$ and the sheaves
of relative ![]() $\mathscr {L}$-valued holomorphic n-forms that are square-integrable with respect to the Kähler form
$\mathscr {L}$-valued holomorphic n-forms that are square-integrable with respect to the Kähler form ![]() $\widetilde {\omega }_{\mathscr {X}'}= \omega _{\mathscr {X}'}+ f^*\omega _S$ and the hermitian metric
$\widetilde {\omega }_{\mathscr {X}'}= \omega _{\mathscr {X}'}+ f^*\omega _S$ and the hermitian metric ![]() $h|_{\mathscr {X}'}$, where integrability does not depend upon the choice of a hermitian form
$h|_{\mathscr {X}'}$, where integrability does not depend upon the choice of a hermitian form ![]() $\omega _S$.
$\omega _S$.
Let
denote the sheaf of ![]() $(0,q)$-currents on the total space
$(0,q)$-currents on the total space ![]() $\mathscr {X}'$with values in the coherent sheaf
$\mathscr {X}'$with values in the coherent sheaf ![]() $\Omega ^n_{\mathscr {X}'/S}(\mathscr {L})$ that are square-integrable along with their exterior
$\Omega ^n_{\mathscr {X}'/S}(\mathscr {L})$ that are square-integrable along with their exterior ![]() $\overline {{\partial }}$-derivatives.
$\overline {{\partial }}$-derivatives.
(i)
 $$ \begin{align*}\mathscr{O}_{(2)}(\Omega^n_{\mathscr{X}'/S}(\mathscr{L}|_{\mathscr{X}'}), \widetilde{\omega}_{\mathscr{X}'},h|_{\mathscr{X}'}) \simeq \Omega^n(\log \mathcal{D})_{\mathscr{X}/S}(\mathscr{L}). \end{align*} $$
$$ \begin{align*}\mathscr{O}_{(2)}(\Omega^n_{\mathscr{X}'/S}(\mathscr{L}|_{\mathscr{X}'}), \widetilde{\omega}_{\mathscr{X}'},h|_{\mathscr{X}'}) \simeq \Omega^n(\log \mathcal{D})_{\mathscr{X}/S}(\mathscr{L}). \end{align*} $$(ii) The complex
is a fine resolution of $$ \begin{align*}(\mathscr{A}^{0,\bullet}_{(2)}(\Omega^n_{\mathscr{X}'/S}(\mathscr{L}),\widetilde{\omega}_{\mathscr{X}'},h|_{\mathscr{X}'}),\overline{{\partial}}) \end{align*} $$
$$ \begin{align*}(\mathscr{A}^{0,\bullet}_{(2)}(\Omega^n_{\mathscr{X}'/S}(\mathscr{L}),\widetilde{\omega}_{\mathscr{X}'},h|_{\mathscr{X}'}),\overline{{\partial}}) \end{align*} $$ $\mathscr {O}_{(2)}(\Omega ^n_{\mathscr {X}'/S}(\mathscr {L}), \widetilde {\omega }_{\mathscr {X}'},h|_{\mathscr {X}'})$.
$\mathscr {O}_{(2)}(\Omega ^n_{\mathscr {X}'/S}(\mathscr {L}), \widetilde {\omega }_{\mathscr {X}'},h|_{\mathscr {X}'})$.
Proof. To simplify notation, we assume that ![]() $\dim S=1$. We note that
$\dim S=1$. We note that
and the function ![]() $\varphi $ is (locally with regard to S uniformly) bounded. For an open set
$\varphi $ is (locally with regard to S uniformly) bounded. For an open set ![]() $U \subset \mathscr {X}$, we thus have for the
$U \subset \mathscr {X}$, we thus have for the ![]() $L^2$-norm of a section
$L^2$-norm of a section ![]() $u \in \Omega ^n_{\mathscr {X}'/S}(\mathscr {L})$ that
$u \in \Omega ^n_{\mathscr {X}'/S}(\mathscr {L})$ that
 $$ \begin{align*} \int_U{|u|^2_{\omega_{\mathscr{X}'/S}, h_{\mathscr{L}}}\;\widetilde\omega_{\mathscr{X}'}^{n+1}} \sim \int_{f(U)}\left(\int_{X_s\cap U}{(u\wedge \overline{u})_h}\right)\omega_S. \end{align*} $$
$$ \begin{align*} \int_U{|u|^2_{\omega_{\mathscr{X}'/S}, h_{\mathscr{L}}}\;\widetilde\omega_{\mathscr{X}'}^{n+1}} \sim \int_{f(U)}\left(\int_{X_s\cap U}{(u\wedge \overline{u})_h}\right)\omega_S. \end{align*} $$The first statement follows from Fubini’s theorem, the fact that nearby fibres and bundles are quasi-isometric, and Proposition 1. For the second statement, we decompose the vector bundle ![]() $\Omega ^n_{\mathscr {X}'/S}(\mathscr {L}|_{\mathscr {X}'})$ locally as a sum of line bundles and apply [Reference Fujiki8, Prop. 2.1]; also compare to [Reference Fujiki8, p.870]. This shows that we have a resolution. By Proposition 2, fibrewise we find cut-off functions with bounded differentials. Because, in the differentiable sense, we have a product situation, this also holds on the total space. Hence, the sheaves of locally
$\Omega ^n_{\mathscr {X}'/S}(\mathscr {L}|_{\mathscr {X}'})$ locally as a sum of line bundles and apply [Reference Fujiki8, Prop. 2.1]; also compare to [Reference Fujiki8, p.870]. This shows that we have a resolution. By Proposition 2, fibrewise we find cut-off functions with bounded differentials. Because, in the differentiable sense, we have a product situation, this also holds on the total space. Hence, the sheaves of locally ![]() $L^2$ integrable smooth sections are again fine.
$L^2$ integrable smooth sections are again fine.
Corollary 4. The (local) holomorphic sections of ![]() $f_*(\Omega ^n(\log \mathcal {D})_{\mathscr {X}/S}(\mathscr {L}))$ are given by holomorphic sections of
$f_*(\Omega ^n(\log \mathcal {D})_{\mathscr {X}/S}(\mathscr {L}))$ are given by holomorphic sections of ![]() $\Omega ^n(\log \mathcal {D})_{\mathscr {X}/S}(\mathscr {L})$ on the total space that are precisely the holomorphic sections of
$\Omega ^n(\log \mathcal {D})_{\mathscr {X}/S}(\mathscr {L})$ on the total space that are precisely the holomorphic sections of ![]() $\Omega ^n_{\mathscr {X}'/S}(\mathscr {L}|_{\mathscr {X}'})$ that are
$\Omega ^n_{\mathscr {X}'/S}(\mathscr {L}|_{\mathscr {X}'})$ that are ![]() $L^2$-integrable along the fibres. In particular, their restrictions to the open fibres yield holomorphic and
$L^2$-integrable along the fibres. In particular, their restrictions to the open fibres yield holomorphic and ![]() $L^2$-integrable
$L^2$-integrable ![]() $(n,0)$-forms with values in L.
$(n,0)$-forms with values in L.
3.7 Fibre integrals and Lie derivatives
Given our family ![]() $f: \mathscr {X}' \to S$ of open complex manifolds
$f: \mathscr {X}' \to S$ of open complex manifolds ![]() $X^{\prime }_s$ of dimension n and a relative
$X^{\prime }_s$ of dimension n and a relative ![]() $(n,n)$-form
$(n,n)$-form ![]() $\eta $ on
$\eta $ on ![]() $\mathscr {X}'$ that is smooth there and integrable along the fibres, the fibre integral
$\mathscr {X}'$ that is smooth there and integrable along the fibres, the fibre integral
gives a function on the base S (see [Reference Schumacher19, Sect. 2.1] and [Reference Greub, Halperin and Vanstone10, Ch. VII] for the general definition of fibre integrals). In our case, the components ![]() $H^{\overline {l} k}$ of the metric tensor on the direct image are defined by such fibre integrals, where
$H^{\overline {l} k}$ of the metric tensor on the direct image are defined by such fibre integrals, where ![]() $\eta $ is given by the inner product/wedge product of the sections
$\eta $ is given by the inner product/wedge product of the sections ![]() $\psi ^k$:
$\psi ^k$:
We want to show that these fibre integrals give smooth functions on the base so that we indeed get a smooth hermitian metric on the direct image we consider. Thus, if ![]() $s^1,\ldots ,s^m$ are local holomorphic coordinates on the base, we need to compute the derivatives
$s^1,\ldots ,s^m$ are local holomorphic coordinates on the base, we need to compute the derivatives
 $$ \begin{align*} \frac{ \partial}{ \partial s^k}\int_{X_s}\eta \quad \mbox{for }1\leq i \leq r \quad\mbox{ and } \quad \frac{ \partial}{ \partial s^{\overline{l}}}\int_{X_s}\eta, \quad \mbox{for } 1\leq l \leq r. \end{align*} $$
$$ \begin{align*} \frac{ \partial}{ \partial s^k}\int_{X_s}\eta \quad \mbox{for }1\leq i \leq r \quad\mbox{ and } \quad \frac{ \partial}{ \partial s^{\overline{l}}}\int_{X_s}\eta, \quad \mbox{for } 1\leq l \leq r. \end{align*} $$This can be done by using Lie derivatives:
Lemma 3.10. For ![]() $1\leq k \leq m$, let
$1\leq k \leq m$, let ![]() $v_k$ be the horizontal lift of
$v_k$ be the horizontal lift of ![]() $ \partial / \partial s^k$. We write
$ \partial / \partial s^k$. We write ![]() $ \partial / \partial s^{\overline {l}}$ for
$ \partial / \partial s^{\overline {l}}$ for ![]() $ \partial / \partial \overline {s^l}$ and
$ \partial / \partial \overline {s^l}$ and ![]() $v_{\overline {l}}$ for
$v_{\overline {l}}$ for ![]() $\overline {v_l}$. Then
$\overline {v_l}$. Then
 $$ \begin{align*}\frac{ \partial}{ \partial s^k}\int_{X^{\prime}_s}\eta = \int_{X^{\prime}_s}L_{v_k}(\eta) \quad \mbox{and} \quad \frac{ \partial}{ \partial s^{\overline{l}}}\int_{X^{\prime}_s}\eta = \int_{X^{\prime}_s}L_{v_{\overline{l}}}(\eta), \end{align*} $$
$$ \begin{align*}\frac{ \partial}{ \partial s^k}\int_{X^{\prime}_s}\eta = \int_{X^{\prime}_s}L_{v_k}(\eta) \quad \mbox{and} \quad \frac{ \partial}{ \partial s^{\overline{l}}}\int_{X^{\prime}_s}\eta = \int_{X^{\prime}_s}L_{v_{\overline{l}}}(\eta), \end{align*} $$where ![]() $L_{v_k}$ and
$L_{v_k}$ and ![]() $L_{v_{\overline {l}}}$ denotes the Lie derivative in the direction of
$L_{v_{\overline {l}}}$ denotes the Lie derivative in the direction of ![]() $v_k$ and
$v_k$ and ![]() $v_{\overline {l}}$, respectively.
$v_{\overline {l}}$, respectively.
Proof. The statement is well-known when the fibres are compact [Reference Naumann17, Lemma 1]. We only have to show that ![]() $L_{v_k}(\eta )$ and
$L_{v_k}(\eta )$ and ![]() $L_{v_{\overline {l}}}(\eta )$ are square integrable. Then the statement follows from the dominated convergence theorem. We only present it for the first. We are using local holomorphic coordinates
$L_{v_{\overline {l}}}(\eta )$ are square integrable. Then the statement follows from the dominated convergence theorem. We only present it for the first. We are using local holomorphic coordinates ![]() $z^1,\ldots ,z^n$ near a point
$z^1,\ldots ,z^n$ near a point ![]() $p \in D_s$ such that
$p \in D_s$ such that ![]() $D_s=\{z^1\cdots z^k=0\}$. Because
$D_s=\{z^1\cdots z^k=0\}$. Because ![]() $\psi ^k,\psi ^l \in H^0(\mathscr {X},\Omega ^n(\log \mathcal {D})_{\mathscr {X}/S}(\mathscr {L}))$ and due to the assumption on the metric h, we have that
$\psi ^k,\psi ^l \in H^0(\mathscr {X},\Omega ^n(\log \mathcal {D})_{\mathscr {X}/S}(\mathscr {L}))$ and due to the assumption on the metric h, we have that
 $$ \begin{align*} \eta_{1\ldots n \overline{1} \ldots \overline{n}} = O\left(\prod_{i=1}^k{\log^2(|z^i|^2)}\right), \end{align*} $$
$$ \begin{align*} \eta_{1\ldots n \overline{1} \ldots \overline{n}} = O\left(\prod_{i=1}^k{\log^2(|z^i|^2)}\right), \end{align*} $$where
Now ![]() $v_k = \partial / \partial _k + a_k^{\alpha }\, \partial / \partial z^{\alpha }$ so that
$v_k = \partial / \partial _k + a_k^{\alpha }\, \partial / \partial z^{\alpha }$ so that
 $$ \begin{align*} L_{v_k}\eta = \left(\eta_{1\ldots n, \overline{1}, \dots \overline{n};k} + \sum_{\alpha=1}^na_k^{\alpha}\eta_{1\ldots n \overline{1} \ldots \overline{n};\alpha} + \sum_{\alpha=1}^n{a_{k;\alpha}^{\alpha} \eta_{1\ldots n \overline{1}\dots \overline{n}}} \right) \;dz^1\wedge \ldots \wedge dz^n \wedge dz^{\overline{1}}\wedge \ldots \wedge dz^{\overline{n}}. \end{align*} $$
$$ \begin{align*} L_{v_k}\eta = \left(\eta_{1\ldots n, \overline{1}, \dots \overline{n};k} + \sum_{\alpha=1}^na_k^{\alpha}\eta_{1\ldots n \overline{1} \ldots \overline{n};\alpha} + \sum_{\alpha=1}^n{a_{k;\alpha}^{\alpha} \eta_{1\ldots n \overline{1}\dots \overline{n}}} \right) \;dz^1\wedge \ldots \wedge dz^n \wedge dz^{\overline{1}}\wedge \ldots \wedge dz^{\overline{n}}. \end{align*} $$Here, ![]() $;$ denotes the covariant derivative. Now, because of
$;$ denotes the covariant derivative. Now, because of
we see that ![]() $L_{v_k}(\eta )$ is indeed integrable.
$L_{v_k}(\eta )$ is indeed integrable.
We see that we can iterate this process so that the fibre integral gives a smooth function on S. But this means the ![]() $L^2$-metric is indeed a smooth metric on
$L^2$-metric is indeed a smooth metric on ![]() $f_*{(\Omega ^n(\log \mathcal {D})_{\mathscr {X}/S}(\mathscr {L})})$. We note here that the square integrability of
$f_*{(\Omega ^n(\log \mathcal {D})_{\mathscr {X}/S}(\mathscr {L})})$. We note here that the square integrability of ![]() $L_v(\eta )$ will also follow from Lemma 6.2.
$L_v(\eta )$ will also follow from Lemma 6.2.
Before we go to the computation of the curvature, which is the most technical part of the article, let us consider the two applications.
4 Families of log-canonically polarised manifolds: (semi-)positivity of the relative canonical bundle
Let ![]() $\mathscr {D} \overset {i}{\hookrightarrow } \mathscr {X} \overset {f}{\rightarrow } S$ be a holomorphic family of log-canonically polarised pairs: that is, a holomorphic family of smooth log pairs
$\mathscr {D} \overset {i}{\hookrightarrow } \mathscr {X} \overset {f}{\rightarrow } S$ be a holomorphic family of log-canonically polarised pairs: that is, a holomorphic family of smooth log pairs ![]() $(X_s,D_s)$ with ample adjoint bundle
$(X_s,D_s)$ with ample adjoint bundle ![]() $K_{X_s} + D_s$. The family is called effectively parametrised if the Kodaira-Spencer map
$K_{X_s} + D_s$. The family is called effectively parametrised if the Kodaira-Spencer map
is injective at all points ![]() $s\in S$.
$s\in S$.
Now let ![]() $\Omega $ be a smooth (relative) volume form on
$\Omega $ be a smooth (relative) volume form on ![]() $\mathscr {X}$. The relative volume form
$\mathscr {X}$. The relative volume form ![]() $\psi :=\Omega /(\prod _i{||\sigma _i||^2 \log ^2||\sigma _i||^2})$ has the property that
$\psi :=\Omega /(\prod _i{||\sigma _i||^2 \log ^2||\sigma _i||^2})$ has the property that ![]() $\tilde {\omega }_s:=-\operatorname {Ric}(\psi |X_s')$ gives a family of complete Kähler metrics of finite volume on the open fibres
$\tilde {\omega }_s:=-\operatorname {Ric}(\psi |X_s')$ gives a family of complete Kähler metrics of finite volume on the open fibres ![]() $X_s'$ such that
$X_s'$ such that ![]() $C^{-1} < \psi /(-\operatorname {Ric}(\psi ))^n<C$ for some constant
$C^{-1} < \psi /(-\operatorname {Ric}(\psi ))^n<C$ for some constant ![]() $C>1$. Let
$C>1$. Let ![]() $\{\omega _s\}_{s \in S}$ be the family of complete Kähler-Einstein metrics on
$\{\omega _s\}_{s \in S}$ be the family of complete Kähler-Einstein metrics on ![]() $X_s'=X_s \setminus D_s$ with constant negative curvature
$X_s'=X_s \setminus D_s$ with constant negative curvature ![]() $-1$ given by [Reference Kobayashi14, Reference Tian, Yau, Yau and Diego21]. When we write
$-1$ given by [Reference Kobayashi14, Reference Tian, Yau, Yau and Diego21]. When we write ![]() $\omega _s = \tilde {\omega }_s + \sqrt {-1}\partial _s\bar \partial _su_s$ on
$\omega _s = \tilde {\omega }_s + \sqrt {-1}\partial _s\bar \partial _su_s$ on ![]() $X_s'$, they fulfill the following Monge-Ampère equation (compare to [Reference Schumacher18, Eq.(1)]):
$X_s'$, they fulfill the following Monge-Ampère equation (compare to [Reference Schumacher18, Eq.(1)]):
Here, ![]() $\{u_s\}_{s \in S}$ is a family of functions in
$\{u_s\}_{s \in S}$ is a family of functions in ![]() $\mathscr {C}^{k,\alpha }(X\setminus D)$ with
$\mathscr {C}^{k,\alpha }(X\setminus D)$ with ![]() $k\geq 6$. By the implicit function theorem applied to the Hölder spaces
$k\geq 6$. By the implicit function theorem applied to the Hölder spaces ![]() $\mathscr {C}^{k,\alpha }(X\setminus D)$ of functions, these functions
$\mathscr {C}^{k,\alpha }(X\setminus D)$ of functions, these functions ![]() $u_s$ depend smoothly on the parameter
$u_s$ depend smoothly on the parameter ![]() $s\in S$ in the sense that the map
$s\in S$ in the sense that the map ![]() $s \mapsto \mathscr {C}^{k,\alpha }$ is indeed Fréchet differentiable (compare to [Reference Schumacher18, Sect. 2.6]). Hence we can consider the relative volume form
$s \mapsto \mathscr {C}^{k,\alpha }$ is indeed Fréchet differentiable (compare to [Reference Schumacher18, Sect. 2.6]). Hence we can consider the relative volume form ![]() $\omega ^n_{\mathscr {X}'/S}$ on
$\omega ^n_{\mathscr {X}'/S}$ on ![]() $\mathscr {X}'=\mathscr {X}\setminus \mathscr {D}$ associated to the family
$\mathscr {X}'=\mathscr {X}\setminus \mathscr {D}$ associated to the family ![]() $\{\omega _s\}_{s \in S}$ as a singular hermitian metric on
$\{\omega _s\}_{s \in S}$ as a singular hermitian metric on ![]() $K_{\mathscr {X}/S}$ whose inverse has Poincaré type singularities along
$K_{\mathscr {X}/S}$ whose inverse has Poincaré type singularities along ![]() $\mathscr {D}$. Its smooth curvature form on
$\mathscr {D}$. Its smooth curvature form on ![]() $\mathscr {X}'$ is given by
$\mathscr {X}'$ is given by
Analogous to the canonically polarised case proved in [Reference Schumacher19], we have the following result:
Theorem 4.1. The form ![]() $\omega _{\mathscr {X}'} \geq 0$ is semi-positive and strictly positive if the family
$\omega _{\mathscr {X}'} \geq 0$ is semi-positive and strictly positive if the family ![]() $\mathscr {D} \overset {i}{\hookrightarrow } \mathscr {X} \overset {f}{\rightarrow } S$ is effectively parametrised.
$\mathscr {D} \overset {i}{\hookrightarrow } \mathscr {X} \overset {f}{\rightarrow } S$ is effectively parametrised.
Proof. The computation from [Reference Schumacher18] can be adopted. We summarise the main points that we need.
Given a coordinate vector field ![]() ${\partial } /{\partial } s^i $ on S and the horizontal lift
${\partial } /{\partial } s^i $ on S and the horizontal lift ![]() $v_i$, define
$v_i$, define
Then
where ![]() $\Box _s$ denotes the (semi-positive) Laplacian and
$\Box _s$ denotes the (semi-positive) Laplacian and ![]() $\|A_i\|(z,s)$ the pointwise norm of the harmonic representative of
$\|A_i\|(z,s)$ the pointwise norm of the harmonic representative of ![]() $\rho _s({\partial }/{\partial } s^i)$.
$\rho _s({\partial }/{\partial } s^i)$.
The results of the previous section imply that the quantities occurring in equation (4.2) are ![]() $\mathscr {C}^{k,\alpha }$-tensors on the total space and also define such tensors when restricted to the fibres of f and class
$\mathscr {C}^{k,\alpha }$-tensors on the total space and also define such tensors when restricted to the fibres of f and class ![]() $C^{\infty }$ on
$C^{\infty }$ on ![]() $\mathscr {X}'$. Yau’s maximum principle [Reference Yau23, Theorem 1] applies to restrictions of equation (4.2) to the fibres of f and immediately yields that
$\mathscr {X}'$. Yau’s maximum principle [Reference Yau23, Theorem 1] applies to restrictions of equation (4.2) to the fibres of f and immediately yields that ![]() $\varphi _{i\overline {\imath }}\geq 0$.
$\varphi _{i\overline {\imath }}\geq 0$.
The integral of equation (4.2) along a fibre yields the Weil-Petersson norm of ![]() ${\partial }/{\partial } s^i|_s$:
${\partial }/{\partial } s^i|_s$:
 $$ \begin{align*} \|{\partial}/{\partial} s^i|_s\|^2_{WP} = \int_{X_s}\|A_i\|^2(z,s) gdV. \end{align*} $$
$$ \begin{align*} \|{\partial}/{\partial} s^i|_s\|^2_{WP} = \int_{X_s}\|A_i\|^2(z,s) gdV. \end{align*} $$(Again, we are using Gaffney’s result.)
Let ![]() $\rho _s({\partial }/{\partial } s^i)\neq 0$: that is,
$\rho _s({\partial }/{\partial } s^i)\neq 0$: that is, ![]() $A_i\neq 0$. One can show that
$A_i\neq 0$. One can show that ![]() $\varphi _{i\overline {\imath }}(z,s)$ has no zeroes. This follows from the lower heat kernel estimate in the complete case, as given in [Reference Sturm20, Cor. 4.3]. This shows that the heat kernel is strictly positive on the fibre
$\varphi _{i\overline {\imath }}(z,s)$ has no zeroes. This follows from the lower heat kernel estimate in the complete case, as given in [Reference Sturm20, Cor. 4.3]. This shows that the heat kernel is strictly positive on the fibre ![]() $X_s'$. Then the argument is the same as in [Reference Schumacher19, Prop. 1], except that we do not have a fixed positive lower bound in terms of the diameter of the fibres.
$X_s'$. Then the argument is the same as in [Reference Schumacher19, Prop. 1], except that we do not have a fixed positive lower bound in terms of the diameter of the fibres.
Corollary 5. For a family of log-canonically polarised manifolds ![]() $\mathscr {D} \overset {i}{\hookrightarrow } \mathscr {X} \overset {f}{\rightarrow } S$ over a compact base S, the relative adjoint bundle
$\mathscr {D} \overset {i}{\hookrightarrow } \mathscr {X} \overset {f}{\rightarrow } S$ over a compact base S, the relative adjoint bundle ![]() $K_{\mathscr {X}/S} \otimes \mathscr {D}$ is nef. If the family is effectively parametrised,
$K_{\mathscr {X}/S} \otimes \mathscr {D}$ is nef. If the family is effectively parametrised, ![]() $K_{\mathscr {X}/S} \otimes \mathscr {D}$ is big.
$K_{\mathscr {X}/S} \otimes \mathscr {D}$ is big.
Proof. We now compute the curvature current of the singular hermitian metric ![]() $(\omega _{\mathscr {X}'/S}^n)^{-1}=(\omega _s^n)^{-1}_{s \in S}$ on
$(\omega _{\mathscr {X}'/S}^n)^{-1}=(\omega _s^n)^{-1}_{s \in S}$ on ![]() $K_{\mathscr {X}/S}$ on the whole
$K_{\mathscr {X}/S}$ on the whole ![]() $\mathscr {X}$. From the Monge-Ampère equation (4.1), we see that the only additional term that vanishes by restricting to
$\mathscr {X}$. From the Monge-Ampère equation (4.1), we see that the only additional term that vanishes by restricting to ![]() $\mathscr {X}'$ is
$\mathscr {X}'$ is ![]() $-\mathscr {D}$, which comes from the term
$-\mathscr {D}$, which comes from the term ![]() $-\sum \partial \bar \partial \log ||\sigma _i||^2$; it is compensated by adding
$-\sum \partial \bar \partial \log ||\sigma _i||^2$; it is compensated by adding ![]() $\mathscr {D}$. This shows that
$\mathscr {D}$. This shows that ![]() $K_{\mathscr {X}/S} \otimes \mathscr {D}$ is pseudoeffective. Here we take the canonical singular metric on
$K_{\mathscr {X}/S} \otimes \mathscr {D}$ is pseudoeffective. Here we take the canonical singular metric on ![]() $\mathscr {D}$. The nefness follows from the fact that the curvature current of the metric on
$\mathscr {D}$. The nefness follows from the fact that the curvature current of the metric on ![]() $K_{\mathscr {X}/S} \otimes \mathscr {D}$ has zero Lelong numbers. The bigness in the effectively parametrised situation then follows from the strict positivity of
$K_{\mathscr {X}/S} \otimes \mathscr {D}$ has zero Lelong numbers. The bigness in the effectively parametrised situation then follows from the strict positivity of ![]() $K_{\mathscr {X}'/S}$ and Boucksom’s bigness criterion [Reference Boucksom2, Cor. 3.3].
$K_{\mathscr {X}'/S}$ and Boucksom’s bigness criterion [Reference Boucksom2, Cor. 3.3].
5 The case of a big line bundle
Let ![]() $E \overset {i}{\hookrightarrow } \mathscr {X} \overset {f}{\rightarrow } S$ be a holomorphic family of smooth log pairs
$E \overset {i}{\hookrightarrow } \mathscr {X} \overset {f}{\rightarrow } S$ be a holomorphic family of smooth log pairs ![]() $(X_s,E_s)$ and F a big line bundle on
$(X_s,E_s)$ and F a big line bundle on ![]() $\mathscr {X}$. We assume that we have a decomposition
$\mathscr {X}$. We assume that we have a decomposition
where A is ample on ![]() $\mathscr {X}$. We choose a smooth positive metric
$\mathscr {X}$. We choose a smooth positive metric ![]() $h_A$ on A and a smooth hermitian metric
$h_A$ on A and a smooth hermitian metric ![]() $h_i$ on each irreducible component
$h_i$ on each irreducible component ![]() $E_i$ of E. Using the canonical section
$E_i$ of E. Using the canonical section ![]() $\sigma _i$ cutting out the divisor
$\sigma _i$ cutting out the divisor ![]() $E_i$, we define another metric on A by setting
$E_i$, we define another metric on A by setting
 $$ \begin{align*} h_{A,\varepsilon} := h_A \cdot \left(\prod_i{|\sigma_i|_{h_i}^2\log^2(|\sigma_i|_{h_i}^2)} \right)^{\varepsilon}. \end{align*} $$
$$ \begin{align*} h_{A,\varepsilon} := h_A \cdot \left(\prod_i{|\sigma_i|_{h_i}^2\log^2(|\sigma_i|_{h_i}^2)} \right)^{\varepsilon}. \end{align*} $$We now make the assumption that there exists an ![]() $\varepsilon>0$ such that
$\varepsilon>0$ such that
In general, such an ![]() $\varepsilon $ need not exist and it depends on the curvatures of
$\varepsilon $ need not exist and it depends on the curvatures of ![]() $h_A$ and
$h_A$ and ![]() $h_i$ on
$h_i$ on ![]() $\mathscr {X}$. Then we can equip F with the metric
$\mathscr {X}$. Then we can equip F with the metric ![]() $h_{F,\varepsilon }$ defined by
$h_{F,\varepsilon }$ defined by
where ![]() $h_{E,\operatorname {sing}}$ is the canonical singular hermitian metric on E given by the section
$h_{E,\operatorname {sing}}$ is the canonical singular hermitian metric on E given by the section ![]() $\sigma =\prod _i{\sigma _i}$. We note that
$\sigma =\prod _i{\sigma _i}$. We note that ![]() $(E,h_{E,\operatorname {sing}})|_{\mathscr {X}'}$ is the trivial line bundle equipped with the trivial metric.
$(E,h_{E,\operatorname {sing}})|_{\mathscr {X}'}$ is the trivial line bundle equipped with the trivial metric.
Now the hermitian bundle ![]() $(A,h_{A,\varepsilon })$ fulfils the requirements of our main theorem (note here that it works with a power
$(A,h_{A,\varepsilon })$ fulfils the requirements of our main theorem (note here that it works with a power ![]() $\varepsilon>0$ instead of
$\varepsilon>0$ instead of ![]() $1$ as well), and we get the Nakano positivity of
$1$ as well), and we get the Nakano positivity of
If we instead apply the general result from [Reference Berndtsson and Păun3] directly to the hermitian bundle ![]() $(F,h_F)$ with
$(F,h_F)$ with ![]() $h_F=h_A \cdot h_{E,\operatorname {sing}}$, we get first that
$h_F=h_A \cdot h_{E,\operatorname {sing}}$, we get first that
is positive in the singular sense of Griffiths. But here we have ![]() $ \mathcal {J}(h_F)=\mathscr {O}(-E)$, so we can conclude that
$ \mathcal {J}(h_F)=\mathscr {O}(-E)$, so we can conclude that
is positive in the sense of Nakano using the result from [Reference Berndtsson1]. Of course, we should mention here that we have
as sheaves but not as hermitian bundles because we changed the metric on A for the larger one. If the decomposition ![]() $F=A+E$ is a relative Zariski decomposition, both sheaves coincide. If one applies [Reference Berndtsson and Păun3] to
$F=A+E$ is a relative Zariski decomposition, both sheaves coincide. If one applies [Reference Berndtsson and Păun3] to ![]() $(L,h_{F,\varepsilon })$ with a trivial multiplier ideal sheaf
$(L,h_{F,\varepsilon })$ with a trivial multiplier ideal sheaf ![]() $\mathcal {J}(h_{F,\varepsilon })$, we get Griffiths positivity of
$\mathcal {J}(h_{F,\varepsilon })$, we get Griffiths positivity of ![]() $f_*(K_{\mathscr {X}/S}+F)$ only in the weaker singular sense.
$f_*(K_{\mathscr {X}/S}+F)$ only in the weaker singular sense.
6 Computation of the curvature
Computing the curvature of the ![]() $L^2$-metric on
$L^2$-metric on ![]() $f_*(\Omega ^n(\log \mathscr {D}))_{\mathscr {X}/S}(\mathscr {L})$ requires taking derivatives in the base direction of fibre integrals, which can be realised by taking Lie derivatives of the integrands. These Lie derivatives can be split up by introducing Lie derivatives of
$f_*(\Omega ^n(\log \mathscr {D}))_{\mathscr {X}/S}(\mathscr {L})$ requires taking derivatives in the base direction of fibre integrals, which can be realised by taking Lie derivatives of the integrands. These Lie derivatives can be split up by introducing Lie derivatives of ![]() $(n,0)$-forms with values in L. They are computed in terms of covariant derivatives with respect to the Chern connection on
$(n,0)$-forms with values in L. They are computed in terms of covariant derivatives with respect to the Chern connection on ![]() $(X^{\prime }_s,\omega _s)$ and the hermitian holomorphic bundle
$(X^{\prime }_s,\omega _s)$ and the hermitian holomorphic bundle ![]() $(L_s,h_s)$. We use the symbol
$(L_s,h_s)$. We use the symbol ![]() $;$ for covariant derivatives and
$;$ for covariant derivatives and ![]() $,$ for ordinary derivatives. Greek letters indicate the fibre direction, whereas Latin indices stand for directions on the base. Because we are dealing with alternating
$,$ for ordinary derivatives. Greek letters indicate the fibre direction, whereas Latin indices stand for directions on the base. Because we are dealing with alternating ![]() $(p,q)$-forms, the coefficients are meant to be skew-symmetric. Thus every such
$(p,q)$-forms, the coefficients are meant to be skew-symmetric. Thus every such ![]() $(p,q)$-form carries a factor
$(p,q)$-form carries a factor ![]() $1/p!q!$, which we suppress in the notation. These factors play a role in the process of skew-symmetrising the coefficients of a
$1/p!q!$, which we suppress in the notation. These factors play a role in the process of skew-symmetrising the coefficients of a ![]() $(p,q)$-form by taking alternating sums of the (not yet skew-symmetric) coefficients. We adopt the Einstein convention of summation.
$(p,q)$-form by taking alternating sums of the (not yet skew-symmetric) coefficients. We adopt the Einstein convention of summation.
6.1 Setup
By polarisation, it is sufficient to treat the case where ![]() $\dim S=1$ for the computation of the curvature, which simplifies the notation. Therefore, we set
$\dim S=1$ for the computation of the curvature, which simplifies the notation. Therefore, we set ![]() $s=s^1, v_s=v_1$, and so on. We write
$s=s^1, v_s=v_1$, and so on. We write ![]() $s,\overline {s}$ for the indices
$s,\overline {s}$ for the indices ![]() $1,\overline {1}$ so that
$1,\overline {1}$ so that
and
We assume local freeness of the sheaf ![]() $f_*(\Omega ^n(\log \mathscr {D}))_{\mathscr {X}/S}(\mathscr {L})$. According to Corollary 4, we can represent local sections of this sheaf by holomorphic sections of
$f_*(\Omega ^n(\log \mathscr {D}))_{\mathscr {X}/S}(\mathscr {L})$. According to Corollary 4, we can represent local sections of this sheaf by holomorphic sections of ![]() $(\Omega ^n(\log \mathcal {D}))_{\mathscr {X}'/S}(\mathscr {L}|_{\mathscr {X}'})$, which restrict to holomorphic and square integrable
$(\Omega ^n(\log \mathcal {D}))_{\mathscr {X}'/S}(\mathscr {L}|_{\mathscr {X}'})$, which restrict to holomorphic and square integrable ![]() $(n,0)$-forms on the open fibres
$(n,0)$-forms on the open fibres ![]() $X^{\prime }_s$. We denote such a section by
$X^{\prime }_s$. We denote such a section by ![]() $\psi $. In local coordinates, we have
$\psi $. In local coordinates, we have
 $$ \begin{align*} \psi|_{X^{\prime}_s} &= \psi_{\alpha_1 \ldots \alpha_n}dz^{\alpha_1}\wedge \ldots dz^{\alpha_n}\\ &= \psi_{A_n}dz^{A_n}, \end{align*} $$
$$ \begin{align*} \psi|_{X^{\prime}_s} &= \psi_{\alpha_1 \ldots \alpha_n}dz^{\alpha_1}\wedge \ldots dz^{\alpha_n}\\ &= \psi_{A_n}dz^{A_n}, \end{align*} $$where ![]() $A_n=(\alpha _1,\ldots ,\alpha _n)$. The
$A_n=(\alpha _1,\ldots ,\alpha _n)$. The ![]() $\bar \partial $-closedness of
$\bar \partial $-closedness of ![]() $\psi $ means
$\psi $ means
6.2 Cup product
Definition 4. Let ![]() $s \in S$ and
$s \in S$ and ![]() $A=A_{s\overline {\beta }}^{\alpha }(z,s) \partial _{\alpha }dz^{\overline {\beta }}$ be the Kodaira-Spencer form on the fibre
$A=A_{s\overline {\beta }}^{\alpha }(z,s) \partial _{\alpha }dz^{\overline {\beta }}$ be the Kodaira-Spencer form on the fibre ![]() $X^{\prime }_s$. The wedge product, together with the contraction, defines a map
$X^{\prime }_s$. The wedge product, together with the contraction, defines a map
which can be described locally by
 $$ \begin{align*} &\quad\left( A_{i\overline{\delta}}^{\gamma} \partial_{\gamma}dz^{\overline{\delta}}\right) \cup \left(\psi_{\alpha_1 \ldots \alpha_n}\;dz^{\alpha_1}\wedge \ldots \wedge dz^{\alpha_n} \right)\\ &= A_{i\overline{\beta}}^{\gamma} \psi_{\gamma\alpha_1\ldots \alpha_{n-1}}\; dz^{\overline{\beta}}\wedge dz^{\alpha_1} \wedge \ldots \wedge dz^{\alpha_{n-1}}. \end{align*} $$
$$ \begin{align*} &\quad\left( A_{i\overline{\delta}}^{\gamma} \partial_{\gamma}dz^{\overline{\delta}}\right) \cup \left(\psi_{\alpha_1 \ldots \alpha_n}\;dz^{\alpha_1}\wedge \ldots \wedge dz^{\alpha_n} \right)\\ &= A_{i\overline{\beta}}^{\gamma} \psi_{\gamma\alpha_1\ldots \alpha_{n-1}}\; dz^{\overline{\beta}}\wedge dz^{\alpha_1} \wedge \ldots \wedge dz^{\alpha_{n-1}}. \end{align*} $$The fact that ![]() $A_i \cup \psi $ is indeed square integrable will be proved in Lemma 6.2.
$A_i \cup \psi $ is indeed square integrable will be proved in Lemma 6.2.
6.3 Lie derivatives
Now we choose a local frame ![]() $\{\psi ^1,\ldots ,\psi ^r\}$ according to Corollary 4. The components of the metric tensor
$\{\psi ^1,\ldots ,\psi ^r\}$ according to Corollary 4. The components of the metric tensor ![]() $H^{\overline {l} k}$ for
$H^{\overline {l} k}$ for ![]() $f_*(\Omega ^n(\log \mathscr {D}))_{\mathscr {X}/S}(\mathscr {L})$ on the base space S are given by
$f_*(\Omega ^n(\log \mathscr {D}))_{\mathscr {X}/S}(\mathscr {L})$ on the base space S are given by
 $$ \begin{align*} H^{\overline{l} k}(s):={\langle}\psi^k,\psi^l{\rangle} :={\langle}\psi^k|_{X^{\prime}_s},\psi^l|_{X^{\prime}_s}{\rangle} = \int_{X^{\prime}_s}{\psi^k_{A_n}\psi^{\overline{l}}_{\overline{B}_n}g^{\overline{B}_nA_n} h|_{X^{\prime}_s}\,dV}. \end{align*} $$
$$ \begin{align*} H^{\overline{l} k}(s):={\langle}\psi^k,\psi^l{\rangle} :={\langle}\psi^k|_{X^{\prime}_s},\psi^l|_{X^{\prime}_s}{\rangle} = \int_{X^{\prime}_s}{\psi^k_{A_n}\psi^{\overline{l}}_{\overline{B}_n}g^{\overline{B}_nA_n} h|_{X^{\prime}_s}\,dV}. \end{align*} $$We also write
for the pointwise inner product of ![]() $L|_{X^{\prime }_s}$-valued
$L|_{X^{\prime }_s}$-valued ![]() $(n,0)$-forms. Here and in the following, we write g for the hermitian metric associated to the complete Kähler from
$(n,0)$-forms. Here and in the following, we write g for the hermitian metric associated to the complete Kähler from ![]() $\omega _s$. When we compute derivatives with respect to the base of these fibre integrals, we apply Lie derivatives with respect to the horizontal lifts of the tangent vectors according to Lemma 3.10. This considerably simplifies the computation. To break up the Lie derivative of the pointwise inner product (which is a relative
$\omega _s$. When we compute derivatives with respect to the base of these fibre integrals, we apply Lie derivatives with respect to the horizontal lifts of the tangent vectors according to Lemma 3.10. This considerably simplifies the computation. To break up the Lie derivative of the pointwise inner product (which is a relative ![]() $(n,n)$-form), we need to introduce Lie derivatives of relative differential forms with values in a line bundle. This can be done by using the hermitian connection
$(n,n)$-form), we need to introduce Lie derivatives of relative differential forms with values in a line bundle. This can be done by using the hermitian connection ![]() $\nabla $ on
$\nabla $ on ![]() $\Lambda ^{n,0}T^*_{\mathscr {X}'/S}\otimes \mathscr {L}|_{\mathscr {X}'}$ induced by the Chern connections on
$\Lambda ^{n,0}T^*_{\mathscr {X}'/S}\otimes \mathscr {L}|_{\mathscr {X}'}$ induced by the Chern connections on ![]() $(T_{X^{\prime }_s},\omega _{X_s})$ and
$(T_{X^{\prime }_s},\omega _{X_s})$ and ![]() $(L_s,h_s)$. We define the Lie derivative of
$(L_s,h_s)$. We define the Lie derivative of ![]() $\psi $ with respect to the horizontal lift v by using Cartan’s formula
$\psi $ with respect to the horizontal lift v by using Cartan’s formula
and similar for the Lie derivative with respect to ![]() $\overline {v}$.
$\overline {v}$.
Taking Lie derivatives is not type-preserving. We have the type decomposition for ![]() $\psi =\psi ^k$ or
$\psi =\psi ^k$ or ![]() $\psi =\psi ^l$ and
$\psi =\psi ^l$ and ![]() $v=v_s$
$v=v_s$
where ![]() $L_v\psi '$ is of type
$L_v\psi '$ is of type ![]() $(n,0)$ and
$(n,0)$ and ![]() $L_v\psi "$ is of type
$L_v\psi "$ is of type ![]() $(n-1,1)$. In local coordinates, we have
$(n-1,1)$. In local coordinates, we have


One justification for using Lie derivatives is given by the following lemma, which allows us to express some components of the Lie derivatives as cup products with the Kodaira-Spencer form:
Lemma 6.1. We have
and it is primitive on the fibres.
Proof. First, we note

To prove that ![]() $A_s \cup \psi $ is primitive, we have to show that
$A_s \cup \psi $ is primitive, we have to show that ![]() $\Lambda _s (A_s\cup \psi )=0$, where
$\Lambda _s (A_s\cup \psi )=0$, where ![]() $\Lambda _s$ is the dual Lefschetz operator with respect to the Kähler form
$\Lambda _s$ is the dual Lefschetz operator with respect to the Kähler form
We have
But now, because ![]() $A^{\alpha \alpha _1}_s=A^{\alpha _1\alpha }_s$ by Lemma 3.9 and
$A^{\alpha \alpha _1}_s=A^{\alpha _1\alpha }_s$ by Lemma 3.9 and ![]() $\psi _{\alpha \,\alpha _1\ldots \alpha _{n-1}}$ is skew-symmetric, we get that
$\psi _{\alpha \,\alpha _1\ldots \alpha _{n-1}}$ is skew-symmetric, we get that
Similarly, we have a type decomposition for the Lie derivative along ![]() $\overline {v} = v_{\overline {s}}$
$\overline {v} = v_{\overline {s}}$
where ![]() $L_{\overline {v}}\psi '$ is of type
$L_{\overline {v}}\psi '$ is of type ![]() $(n,0)$ and
$(n,0)$ and ![]() $L_{\overline {v}}\psi "$ is of type
$L_{\overline {v}}\psi "$ is of type ![]() $(n+1,n-1)$ and hence vanishes by degree reasons. In local coordinates, this is
$(n+1,n-1)$ and hence vanishes by degree reasons. In local coordinates, this is

From this, we infer that ![]() $L_{\overline {v}}\psi =L_{\overline {v}}\psi '=0$ because
$L_{\overline {v}}\psi =L_{\overline {v}}\psi '=0$ because ![]() $\psi $ is holomorphic. The type decomposition can be verified using the definition given by equation (6.2). We refer the reader to [Reference Naumann17] for verification.
$\psi $ is holomorphic. The type decomposition can be verified using the definition given by equation (6.2). We refer the reader to [Reference Naumann17] for verification.
Lemma 6.2. The smooth forms ![]() $L_v \psi '$ and
$L_v \psi '$ and ![]() $L_v\psi "$ are
$L_v\psi "$ are ![]() $L^2$-integrable.
$L^2$-integrable.
Proof. We use local coordinates ![]() $z^1,\ldots ,z^n$ in a neighbourhood U of a point
$z^1,\ldots ,z^n$ in a neighbourhood U of a point ![]() $p \in D_s \subset X_s$, where
$p \in D_s \subset X_s$, where ![]() $D_s \cap U = \{z^1\cdots z^k=0\}$. We now have
$D_s \cap U = \{z^1\cdots z^k=0\}$. We now have
 $$ \begin{align*}\psi_{A_n} = O\left(\frac{1}{|z^1\cdots z^k|}\right) \end{align*} $$
$$ \begin{align*}\psi_{A_n} = O\left(\frac{1}{|z^1\cdots z^k|}\right) \end{align*} $$and
From the local expression (6.3), we thus see that
 $$ \begin{align*} (L_v\psi)^{\prime}_{A_n} = O\left(\frac{1}{|z^1\cdots z^k|}\right), \end{align*} $$
$$ \begin{align*} (L_v\psi)^{\prime}_{A_n} = O\left(\frac{1}{|z^1\cdots z^k|}\right), \end{align*} $$so it is again square integrable.
To prove that ![]() $L_v\psi "$ is square integrable is more complicated. We first look at the order of
$L_v\psi "$ is square integrable is more complicated. We first look at the order of ![]() $A^{\alpha }_{s\overline {\beta }}$:
$A^{\alpha }_{s\overline {\beta }}$:
 $$ \begin{align*} A^{\alpha}_{\overline{\beta}} &= O(1) \quad \mbox{for} \quad 1\leq \alpha=\beta \leq k \quad \mbox{or } \quad k+1 \leq \alpha,\beta \leq n.\\ A^{\alpha}_{\overline{\beta}} &= O\left(\frac{1}{|z^{\beta}|\log |z^{\beta}|}\right) \quad \mbox{for} \quad \alpha>k \mbox{ and } \beta\leq k. \\ A^{\alpha}_{\overline{\beta}} &= O\left(|z^{\alpha}|\log |z^{\alpha}|\right) \quad \mbox{for} \quad \alpha \leq k \mbox{ and } \beta > k. \\ A^{\alpha}_{\overline{\beta}} &= O\left(\frac{|z^{\alpha}|\log |z^{\alpha}|}{|z^{\beta}|\log |z^{\beta}|}\right) \quad \mbox{for} \quad 1 \leq \alpha\neq \beta \leq k. \end{align*} $$
$$ \begin{align*} A^{\alpha}_{\overline{\beta}} &= O(1) \quad \mbox{for} \quad 1\leq \alpha=\beta \leq k \quad \mbox{or } \quad k+1 \leq \alpha,\beta \leq n.\\ A^{\alpha}_{\overline{\beta}} &= O\left(\frac{1}{|z^{\beta}|\log |z^{\beta}|}\right) \quad \mbox{for} \quad \alpha>k \mbox{ and } \beta\leq k. \\ A^{\alpha}_{\overline{\beta}} &= O\left(|z^{\alpha}|\log |z^{\alpha}|\right) \quad \mbox{for} \quad \alpha \leq k \mbox{ and } \beta > k. \\ A^{\alpha}_{\overline{\beta}} &= O\left(\frac{|z^{\alpha}|\log |z^{\alpha}|}{|z^{\beta}|\log |z^{\beta}|}\right) \quad \mbox{for} \quad 1 \leq \alpha\neq \beta \leq k. \end{align*} $$To prove that ![]() $L_v\psi "=A_s \cup \psi $ is
$L_v\psi "=A_s \cup \psi $ is ![]() $L^2$-integrable means to verify that
$L^2$-integrable means to verify that
 $$ \begin{align*} \int_{X^{\prime}_s}{(A_s \cup \psi) \wedge \overline{(A_s \cup\psi)}} \end{align*} $$
$$ \begin{align*} \int_{X^{\prime}_s}{(A_s \cup \psi) \wedge \overline{(A_s \cup\psi)}} \end{align*} $$is finite because the form is primitive by Lemma 6.1. For this we first note that the sum in the expression of ![]() $(A_s \cup \psi )_{\overline {\beta }_n\alpha _1\ldots \alpha _{n-1}}$ reduces to
$(A_s \cup \psi )_{\overline {\beta }_n\alpha _1\ldots \alpha _{n-1}}$ reduces to
The only really critical term in ![]() $(A_s \cup \psi )_{\overline {\beta }_n\alpha _1\ldots \alpha _{n-1}}$ occurs if
$(A_s \cup \psi )_{\overline {\beta }_n\alpha _1\ldots \alpha _{n-1}}$ occurs if ![]() $\alpha _n \in \{k+1,\dots ,n\}$,
$\alpha _n \in \{k+1,\dots ,n\}$, ![]() $\beta _n \in \{1,\ldots ,k\}$ and
$\beta _n \in \{1,\ldots ,k\}$ and ![]() $\beta _n$ is among the
$\beta _n$ is among the ![]() $\alpha _1,\ldots , \alpha _{n-1}$, because in this case the order in
$\alpha _1,\ldots , \alpha _{n-1}$, because in this case the order in ![]() $z^{\beta _n}$ is
$z^{\beta _n}$ is
But then, in the above integral, this term can only be paired with another term that contains neither ![]() $dz^{\beta _n}$ nor
$dz^{\beta _n}$ nor ![]() $dz^{\overline {\beta }_n}$. So we see that the product
$dz^{\overline {\beta }_n}$. So we see that the product ![]() $(A_s \cup \psi ) \wedge \overline {(A_s \cup \psi )}$ remains integrable.
$(A_s \cup \psi ) \wedge \overline {(A_s \cup \psi )}$ remains integrable.
We need the following lemma:
Lemma 6.3. The Lie derivative of the volume element ![]() $dV=\omega _s^n/n!$ along the horizontal lift v vanishes: that is,
$dV=\omega _s^n/n!$ along the horizontal lift v vanishes: that is,
Proof. It suffices to show that the ![]() $(1,1)$ component of
$(1,1)$ component of ![]() $L_v(g_{\alpha \overline {\beta }})$ vanishes, which implies
$L_v(g_{\alpha \overline {\beta }})$ vanishes, which implies ![]() $L_v(\det (g_{\alpha \overline {\beta }}))=0.$ We have
$L_v(\det (g_{\alpha \overline {\beta }}))=0.$ We have
6.4 Main part of the computation
We start computing the curvature by computing the first-order variation. Using Lie derivatives, the pointwise inner products can be broken up:
where ![]() $ \partial / \partial s$ denotes a tangent vector on the base S and v its horizontal lift and analogous for
$ \partial / \partial s$ denotes a tangent vector on the base S and v its horizontal lift and analogous for ![]() $ \partial / \partial \overline {s}$.
$ \partial / \partial \overline {s}$.
Proof. We first apply Lemma 3.10 and get that
 $$ \begin{align*} \frac{ \partial}{ \partial s} {\langle}\psi^k,\psi^l{\rangle} (s) = \int_{X^{\prime}_s}{L_v(\psi^k \cdot \psi^{\overline{l}}\; dV)} = \int_{X^{\prime}_s}{L_v(\psi^k \cdot \psi^{\overline{l}})\; dV} \end{align*} $$
$$ \begin{align*} \frac{ \partial}{ \partial s} {\langle}\psi^k,\psi^l{\rangle} (s) = \int_{X^{\prime}_s}{L_v(\psi^k \cdot \psi^{\overline{l}}\; dV)} = \int_{X^{\prime}_s}{L_v(\psi^k \cdot \psi^{\overline{l}})\; dV} \end{align*} $$by Lemma 6.3. Now it follows by a direct computation (see [Reference Naumann17, Prop.1]) that
so that
because ![]() $L_{\overline {v}}\psi ^l=0$.
$L_{\overline {v}}\psi ^l=0$.
The above proposition is the primary reason for the use of Lie derivatives. For later computations, we need to compare Laplacians:
Lemma 6.4. We have the following relation on the space ![]() $A^{p,q}_{(2)}(X^{\prime }_s,L_s)$:
$A^{p,q}_{(2)}(X^{\prime }_s,L_s)$:
In particular, the harmonic forms ![]() $\psi \in A^{n,0}_{(2)}(X^{\prime }_s,L_s)$ are also harmonic with respect to
$\psi \in A^{n,0}_{(2)}(X^{\prime }_s,L_s)$ are also harmonic with respect to ![]() $ \partial $, which is the
$ \partial $, which is the ![]() $(1,0)$- part of the hermitian connection on
$(1,0)$- part of the hermitian connection on ![]() $A^{n,0}_{(2)}(X^{\prime }_s,L_s)$.
$A^{n,0}_{(2)}(X^{\prime }_s,L_s)$.
Proof. The Bochner-Kodaira-Nakano identity says (on the fibre ![]() $X^{\prime }_s$)
$X^{\prime }_s$)
But by definition, we have ![]() $\omega _{X_s}=\sqrt {-1}\Theta (L_s)$. Furthermore, it holds (see [Reference Demailly7, Cor.VI.5.9])
$\omega _{X_s}=\sqrt {-1}\Theta (L_s)$. Furthermore, it holds (see [Reference Demailly7, Cor.VI.5.9])
Next, we start to compute the second-order derivative of ![]() $H^{\overline {l} k}$ and begin with
$H^{\overline {l} k}$ and begin with
We obtain
 $$ \begin{align*} \partial_{\overline{s}} \partial_s {\langle}\psi^k,\psi^l{\rangle} &= {\langle}L_{\overline{v}}L_v\psi^k,\psi^l{\rangle} + {\langle}L_v\psi^k,L_v\psi^l{\rangle}\\ &= {\langle}(L_{[\overline{v},v]} + \Theta(L|_{\mathscr{X}'})_{\overline{v} v})\psi^k, \psi^l{\rangle} + {\langle}L_vL_{\overline{v}}\psi^k,\psi^l{\rangle} + {\langle}L_v\psi^k,L_v\psi^l{\rangle}\\ &= {\langle}(L_{[\overline{v},v]} + \Theta(L|_{\mathscr{X}'})_{\overline{v} v})\psi^k, \psi^l{\rangle} + \partial_s{\langle}L_{\overline{v}}\psi^k,\psi^l{\rangle} - {\langle}L_{\overline{v}}\psi^k,L_{\overline{v}}\psi^l{\rangle} + {\langle}L_v\psi^k,L_v\psi^l{\rangle}. \end{align*} $$
$$ \begin{align*} \partial_{\overline{s}} \partial_s {\langle}\psi^k,\psi^l{\rangle} &= {\langle}L_{\overline{v}}L_v\psi^k,\psi^l{\rangle} + {\langle}L_v\psi^k,L_v\psi^l{\rangle}\\ &= {\langle}(L_{[\overline{v},v]} + \Theta(L|_{\mathscr{X}'})_{\overline{v} v})\psi^k, \psi^l{\rangle} + {\langle}L_vL_{\overline{v}}\psi^k,\psi^l{\rangle} + {\langle}L_v\psi^k,L_v\psi^l{\rangle}\\ &= {\langle}(L_{[\overline{v},v]} + \Theta(L|_{\mathscr{X}'})_{\overline{v} v})\psi^k, \psi^l{\rangle} + \partial_s{\langle}L_{\overline{v}}\psi^k,\psi^l{\rangle} - {\langle}L_{\overline{v}}\psi^k,L_{\overline{v}}\psi^l{\rangle} + {\langle}L_v\psi^k,L_v\psi^l{\rangle}. \end{align*} $$Because of ![]() $L_{\overline {v}}\psi ^k \equiv 0$, as we just saw, we get
$L_{\overline {v}}\psi ^k \equiv 0$, as we just saw, we get
We will see below that the smooth ![]() $(n,0)$-form
$(n,0)$-form ![]() $(L_{[\overline {v},v]} + \Theta (L|_{\mathscr {X}'})_{\overline {v} v})\psi ^k$ is indeed square integrable, which justifies that
$(L_{[\overline {v},v]} + \Theta (L|_{\mathscr {X}'})_{\overline {v} v})\psi ^k$ is indeed square integrable, which justifies that ![]() $L_{\overline {v}}L_v \psi ^k$ is square integrable, too.
$L_{\overline {v}}L_v \psi ^k$ is square integrable, too.
Now we treat each term on the right-hand side of equation (6.8) separately. For the first summand, we have
where the bracket ![]() $[w,\rule {0.3cm}{0.4pt}]$ stands for a Lie derivative along the vector field w.
$[w,\rule {0.3cm}{0.4pt}]$ stands for a Lie derivative along the vector field w.
Proof. We first compute the vector field ![]() $[\overline {v},v]$:
$[\overline {v},v]$:
 $$ \begin{align*} [\overline{v},v] &= [ \partial_{\overline{s}} + a_{\overline{s}}^{\overline{\beta}} \partial_{\overline{s}}, \partial_s + a_s^{\alpha} \partial_{\alpha}] \\ &= \left( \partial_{\overline{s}}(a_s^{\alpha}) + a_{\overline{s}}^{\overline{\beta}}a_{a|\overline{\beta}}^{\alpha} \right) \partial_{\alpha} - \left( \partial_s(a_{\overline{s}}^{\overline{\beta}}) + a_s^{\alpha}a_{\overline{s}|\alpha}^{\overline{\beta}} \right) \partial_{\overline{\beta}}. \end{align*} $$
$$ \begin{align*} [\overline{v},v] &= [ \partial_{\overline{s}} + a_{\overline{s}}^{\overline{\beta}} \partial_{\overline{s}}, \partial_s + a_s^{\alpha} \partial_{\alpha}] \\ &= \left( \partial_{\overline{s}}(a_s^{\alpha}) + a_{\overline{s}}^{\overline{\beta}}a_{a|\overline{\beta}}^{\alpha} \right) \partial_{\alpha} - \left( \partial_s(a_{\overline{s}}^{\overline{\beta}}) + a_s^{\alpha}a_{\overline{s}|\alpha}^{\overline{\beta}} \right) \partial_{\overline{\beta}}. \end{align*} $$Now we have
 $$ \begin{align*} \partial_{\overline{s}}(a_s^{\alpha}) &= - \partial_{\overline{s}}(g^{\overline{\beta}\alpha}g_{s\overline{\beta}}) = g^{\overline{\beta}\sigma}g_{\sigma\overline{s}|\overline{\tau}}g^{\overline{\tau}\alpha}g_{s\overline{\beta}} - g^{\overline{\beta}\alpha}g_{s\overline{\beta}|s}\\ &= g^{\overline{\beta}\sigma}a_{\overline{s}\sigma;\overline{\tau}}g^{\overline{\tau}\alpha}a_{s\overline{\beta}} - g^{\overline{\beta}\alpha}g_{s\overline{s};\overline{\beta}}. \end{align*} $$
$$ \begin{align*} \partial_{\overline{s}}(a_s^{\alpha}) &= - \partial_{\overline{s}}(g^{\overline{\beta}\alpha}g_{s\overline{\beta}}) = g^{\overline{\beta}\sigma}g_{\sigma\overline{s}|\overline{\tau}}g^{\overline{\tau}\alpha}g_{s\overline{\beta}} - g^{\overline{\beta}\alpha}g_{s\overline{\beta}|s}\\ &= g^{\overline{\beta}\sigma}a_{\overline{s}\sigma;\overline{\tau}}g^{\overline{\tau}\alpha}a_{s\overline{\beta}} - g^{\overline{\beta}\alpha}g_{s\overline{s};\overline{\beta}}. \end{align*} $$Because of ![]() $\varphi = g_{s\overline {s}} - g_{\alpha \overline {s}}g_{s\overline {\beta }}g^{\overline {\beta }\alpha }$, the coefficient of
$\varphi = g_{s\overline {s}} - g_{\alpha \overline {s}}g_{s\overline {\beta }}g^{\overline {\beta }\alpha }$, the coefficient of ![]() $ \partial _{\alpha }$ is
$ \partial _{\alpha }$ is ![]() $g^{\overline {\beta }\alpha }\varphi _{;\overline {\beta }}=\varphi ^{;\alpha }$. In the same way, we get the coefficient of
$g^{\overline {\beta }\alpha }\varphi _{;\overline {\beta }}=\varphi ^{;\alpha }$. In the same way, we get the coefficient of ![]() $ \partial _{\overline {\beta }}$. Next, we need to compute the contribution of the connection on
$ \partial _{\overline {\beta }}$. Next, we need to compute the contribution of the connection on ![]() $L|_{\mathscr {X}'}$. Because of
$L|_{\mathscr {X}'}$. Because of ![]() $\sqrt {-1}[ \partial ,\bar \partial ]=\sqrt {-1}\Theta (L)|_{\mathscr {X}'}=\omega _{\mathscr {X}'}$, we have
$\sqrt {-1}[ \partial ,\bar \partial ]=\sqrt {-1}\Theta (L)|_{\mathscr {X}'}=\omega _{\mathscr {X}'}$, we have
 $$ \begin{align*} \Theta(L|_{\mathscr{X}'})_{\overline{v} v} &= -\Theta(L|_{\mathscr{X}'})_{v \overline{v}}\\ &= -\left(g_{s\overline{s}} + a_{\overline{s}}^{\overline{\beta}}g_{s\overline{\beta}} + a_s^{\alpha} g_{\alpha \overline{s}} + a_{\overline{s}}^{\overline{\beta}}a_s^{\alpha}g_{\alpha\overline{\beta}}\right)\\ &= -\varphi.\\[-36pt] \end{align*} $$
$$ \begin{align*} \Theta(L|_{\mathscr{X}'})_{\overline{v} v} &= -\Theta(L|_{\mathscr{X}'})_{v \overline{v}}\\ &= -\left(g_{s\overline{s}} + a_{\overline{s}}^{\overline{\beta}}g_{s\overline{\beta}} + a_s^{\alpha} g_{\alpha \overline{s}} + a_{\overline{s}}^{\overline{\beta}}a_s^{\alpha}g_{\alpha\overline{\beta}}\right)\\ &= -\varphi.\\[-36pt] \end{align*} $$ $$ \begin{align} {\langle}(L_{[\overline{v},v]}+ \Theta(L|_{\mathscr{X}'})_{\overline{v} v})\psi^k,\psi^l{\rangle} = -{\langle}\varphi \cdot\psi^k,\psi^l{\rangle} = -\int_{X^{\prime}_s}{\varphi\cdot(\psi^k\cdot\psi^{\overline{l}})\,dV}. \end{align} $$
$$ \begin{align} {\langle}(L_{[\overline{v},v]}+ \Theta(L|_{\mathscr{X}'})_{\overline{v} v})\psi^k,\psi^l{\rangle} = -{\langle}\varphi \cdot\psi^k,\psi^l{\rangle} = -\int_{X^{\prime}_s}{\varphi\cdot(\psi^k\cdot\psi^{\overline{l}})\,dV}. \end{align} $$Proof. The ![]() $ \partial $-closedness of
$ \partial $-closedness of ![]() $\psi ^k$ means
$\psi ^k$ means

Thus

It is clear that ![]() $(\varphi ^{;\alpha } \partial _{\alpha }\cup \psi ^k)$ is square integrable, because
$(\varphi ^{;\alpha } \partial _{\alpha }\cup \psi ^k)$ is square integrable, because ![]() $\varphi |_{X^{\prime }_s}$ lies in
$\varphi |_{X^{\prime }_s}$ lies in ![]() $\mathscr {C}^{k,\alpha }(X^{\prime }_s)$. Moreover, it guarantees that this form lies in the domain of
$\mathscr {C}^{k,\alpha }(X^{\prime }_s)$. Moreover, it guarantees that this form lies in the domain of ![]() $ \partial $. This leads to
$ \partial $. This leads to
 $$ \begin{align*} {\langle}[\varphi^{;\alpha} \partial_{\alpha},\psi^k_{A_n}],\psi^l{\rangle} &= {\langle}[\varphi^{;\alpha} \partial_{\alpha},\psi^k_{A_n}]',\psi^l{\rangle}\\ &= {\langle} \partial\left(\varphi^{;\alpha} \partial_{\alpha}\cup \psi^k\right),\psi^l{\rangle} = {\langle}\varphi^{;\alpha} \partial_{\alpha}\cup \psi^k, \partial^*\psi^l{\rangle} =0. \end{align*} $$
$$ \begin{align*} {\langle}[\varphi^{;\alpha} \partial_{\alpha},\psi^k_{A_n}],\psi^l{\rangle} &= {\langle}[\varphi^{;\alpha} \partial_{\alpha},\psi^k_{A_n}]',\psi^l{\rangle}\\ &= {\langle} \partial\left(\varphi^{;\alpha} \partial_{\alpha}\cup \psi^k\right),\psi^l{\rangle} = {\langle}\varphi^{;\alpha} \partial_{\alpha}\cup \psi^k, \partial^*\psi^l{\rangle} =0. \end{align*} $$Note that by Gaffney’s theorem, Proposition 5, the formal adjoint of ![]() $ \partial $ is equal to the adjoint operator.
$ \partial $ is equal to the adjoint operator.
In the same way, we get
The following proposition contains important identities that allow us to obtain an intrinsic expression for the curvature:
We note that here the operators ![]() $ \partial ,\bar \partial , \partial ^*$ and
$ \partial ,\bar \partial , \partial ^*$ and ![]() $\bar \partial ^*$ mean the fibrewise operators, because we are always dealing with relative forms. For a proof, we refer to [Reference Naumann17, Appendix A]. We see from the proof of Lemma 6.2 that
$\bar \partial ^*$ mean the fibrewise operators, because we are always dealing with relative forms. For a proof, we refer to [Reference Naumann17, Appendix A]. We see from the proof of Lemma 6.2 that ![]() $\bar \partial (L_v \psi ^k)'$ is again square integrable.
$\bar \partial (L_v \psi ^k)'$ is again square integrable.
Now we look at the second term in equation (6.8) and decompose it into its two types
 $$ \begin{align*} {\langle}L_v\psi^k,L_v\psi^l{\rangle} &= {\langle}(L_v\psi^k)',(L_v\psi^l)'{\rangle} - {\langle}(L_v\psi^k)",(L_v\psi^l)"{\rangle}\\ &= {\langle}(L_v\psi^k)',(L_v\psi^l)'{\rangle} - {\langle}A_s \cup \psi^k, A_s \cup \psi^l{\rangle} \end{align*} $$
$$ \begin{align*} {\langle}L_v\psi^k,L_v\psi^l{\rangle} &= {\langle}(L_v\psi^k)',(L_v\psi^l)'{\rangle} - {\langle}(L_v\psi^k)",(L_v\psi^l)"{\rangle}\\ &= {\langle}(L_v\psi^k)',(L_v\psi^l)'{\rangle} - {\langle}A_s \cup \psi^k, A_s \cup \psi^l{\rangle} \end{align*} $$because of equation (6.5).
Now let ![]() $G_{ \partial }$ and
$G_{ \partial }$ and ![]() $G_{\bar \partial }$ be the Green operators on the spaces
$G_{\bar \partial }$ be the Green operators on the spaces ![]() $A^{p,q}_{(2)}(X^{\prime }_s,L|_{X^{\prime }_s})$ with respect to
$A^{p,q}_{(2)}(X^{\prime }_s,L|_{X^{\prime }_s})$ with respect to ![]() $\Box _{\partial }$ and
$\Box _{\partial }$ and ![]() $\Box _{\bar \partial }$, respectively. According to Lemma 6.4, they coincide for
$\Box _{\bar \partial }$, respectively. According to Lemma 6.4, they coincide for ![]() $p+q=n$. We use normal coordinates (of the second kind) at a given point
$p+q=n$. We use normal coordinates (of the second kind) at a given point ![]() $s_0 \in S$. The condition
$s_0 \in S$. The condition ![]() $( \partial / \partial s)H^{\overline {l} k}|_{s_0}=0$ for all
$( \partial / \partial s)H^{\overline {l} k}|_{s_0}=0$ for all ![]() $k,l$ means for
$k,l$ means for ![]() $s=s_0$ the harmonic projection
$s=s_0$ the harmonic projection
vanishes for all k. Thus, using the identity ![]() $\operatorname {id} = H + G_{\bar \partial }\Box _{\bar \partial }$, we can write
$\operatorname {id} = H + G_{\bar \partial }\Box _{\bar \partial }$, we can write
by equations (6.12) and (6.11). Because the form ![]() $\bar \partial (L_v\psi ^k)'= \partial (A_s \cup \psi ^k)$ is of type
$\bar \partial (L_v\psi ^k)'= \partial (A_s \cup \psi ^k)$ is of type ![]() $(n,1)$, we have
$(n,1)$, we have ![]() $G_{\bar \partial }=(\Box _{\partial } + 1)^{-1}$ on such forms by Lemma 6.4. We proceed by
$G_{\bar \partial }=(\Box _{\partial } + 1)^{-1}$ on such forms by Lemma 6.4. We proceed by
 $$ \begin{align*} {\langle}(L_v\psi^k)',(L_v\psi^l)'{\rangle} &= {\langle}\bar \partial^*G_{\bar \partial} \partial(A_s \cup \psi^k),(L_v\psi^l)'{\rangle}\\ &= {\langle}G_{\bar \partial} \partial(A_s \cup \psi^k), \partial(A_s \cup \psi^l){\rangle}\\ &= {\langle}(\Box_{\partial} + 1)^{-1} \partial(A_s \cup \psi^k), \partial(A_s \cup \psi^l){\rangle}\\ &= {\langle} \partial^*(\Box_{\partial} + 1)^{-1} \partial(A_s \cup \psi^k),A_s \cup \psi^l{\rangle}. \end{align*} $$
$$ \begin{align*} {\langle}(L_v\psi^k)',(L_v\psi^l)'{\rangle} &= {\langle}\bar \partial^*G_{\bar \partial} \partial(A_s \cup \psi^k),(L_v\psi^l)'{\rangle}\\ &= {\langle}G_{\bar \partial} \partial(A_s \cup \psi^k), \partial(A_s \cup \psi^l){\rangle}\\ &= {\langle}(\Box_{\partial} + 1)^{-1} \partial(A_s \cup \psi^k), \partial(A_s \cup \psi^l){\rangle}\\ &= {\langle} \partial^*(\Box_{\partial} + 1)^{-1} \partial(A_s \cup \psi^k),A_s \cup \psi^l{\rangle}. \end{align*} $$Again, we used Gaffney’s theorem. Now using equation (6.13) gives
 $$ \begin{align*} {\langle}(L_v\psi^k)',(L_v\psi^l)'{\rangle} &= {\langle}(\Box_{\partial} + 1)^{-1}\Box_{\partial}(A_s \cup \psi^k),A_s \cup \psi^l{\rangle}\\ &= {\langle}(\Box_{\partial} + 1)^{-1}(\Box_{\partial} + 1 - 1) (A_s \cup \psi^k),A_s \cup \psi^l{\rangle}\\ &= {\langle}A_s \cup \psi^k,A_s \cup \psi^l{\rangle} - {\langle}(\Box_{\partial} + 1)^{-1}(A_s \cup \psi^k),A_s \cup \psi^l{\rangle}. \end{align*} $$
$$ \begin{align*} {\langle}(L_v\psi^k)',(L_v\psi^l)'{\rangle} &= {\langle}(\Box_{\partial} + 1)^{-1}\Box_{\partial}(A_s \cup \psi^k),A_s \cup \psi^l{\rangle}\\ &= {\langle}(\Box_{\partial} + 1)^{-1}(\Box_{\partial} + 1 - 1) (A_s \cup \psi^k),A_s \cup \psi^l{\rangle}\\ &= {\langle}A_s \cup \psi^k,A_s \cup \psi^l{\rangle} - {\langle}(\Box_{\partial} + 1)^{-1}(A_s \cup \psi^k),A_s \cup \psi^l{\rangle}. \end{align*} $$Altogether, we have
 $$ \begin{align} {\langle}L_v\psi^k,L_v\psi^l{\rangle} = - \int_{X^{\prime}_s}{(\Box + 1)^{-1}(A_s \cup \psi^k)\cdot (A_{\overline{s}} \cup \psi^{\overline{l}})\, g\, dV}. \end{align} $$
$$ \begin{align} {\langle}L_v\psi^k,L_v\psi^l{\rangle} = - \int_{X^{\prime}_s}{(\Box + 1)^{-1}(A_s \cup \psi^k)\cdot (A_{\overline{s}} \cup \psi^{\overline{l}})\, g\, dV}. \end{align} $$(We write ![]() $\Box =\Box _{\partial }=\Box _{\bar \partial }$ when applied to
$\Box =\Box _{\partial }=\Box _{\bar \partial }$ when applied to ![]() $(n-1,1)$-forms.)
$(n-1,1)$-forms.)
Now our main result Theorem 2.1 follows from equations (6.8), (6.10), (6.14) and the fact that ![]() $R^{\overline {l} k}_{i\overline {\jmath }}(s_0)=- \partial _{\overline {\jmath }} \partial _i H^{\overline {l} k}(s_0)$ in normal coordinates at a point
$R^{\overline {l} k}_{i\overline {\jmath }}(s_0)=- \partial _{\overline {\jmath }} \partial _i H^{\overline {l} k}(s_0)$ in normal coordinates at a point ![]() $s_0 \in S$.
$s_0 \in S$.
Acknowledgements
The author would like to sincerely thank Georg Schumacher for numerous useful discussions about his article [Reference Schumacher18] and Mihai Păun for his comments and interest in this article.
Conflicts of Interest
None.
Funding statement
Publication costs are partially funded by the Open Access Publication Funding of the University of Bayreuth.