Hostname: page-component-8448b6f56d-c4f8m Total loading time: 0 Render date: 2024-04-16T21:30:35.818Z Has data issue: false hasContentIssue false
  • English
  • Français

LOGARITHMIC DE RHAM COMPARISON FOR OPEN RIGID SPACES

Part of: Cycles and subschemes Arithmetic problems. Diophantine geometry Compact analytic spaces

Published online by Cambridge University Press:  25 September 2019

SHIZHANG LI  and
XUANYU PAN
SHIZHANG LI
Affiliation:
Department of Mathematics, Columbia University, MC 4406, 2990 Broadway, New York, NY 10027, USA; shanbei@math.columbia.edu
XUANYU PAN
Affiliation:
Institute of Mathematics, AMSS, Chinese Academy of Sciences, 55 ZhongGuanCun East Road, Beijing 100190, China Max Planck Institute for Mathematics, Vivatsgasse 7, Bonn, 53111, Germany; pan@amss.ac.cn, panxuanyu@mpim-bonn.mpg.de

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this note, we prove the logarithmic 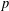$p$-adic comparison theorem for open rigid analytic varieties. We prove that a smooth rigid analytic variety with a strict simple normal crossing divisor is locally $K(\unicode[STIX]{x1D70B},1)$ (in a certain sense) with respect to 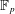$\mathbb{F}_{p}$-local systems and ramified coverings along the divisor. We follow Scholze’s method to produce a pro-version of the Faltings site and use this site to prove a primitive comparison theorem in our setting. After introducing period sheaves in our setting, we prove aforesaid comparison theorem.

MSC classification

Primary: 14G22: Rigid analytic geometry 14C30: Transcendental methods, Hodge theory , Hodge conjecture
Secondary: 14G20: Local ground fields 32J27: Compact Kähler manifolds
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 7 , 2019 , e32
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2019

References

Abbes, A., Gros, M. and Tsuji, T., The p-adic Simpson Correspondence, Annals of Mathematics Studies, 193 (Princeton University Press, Princeton, NJ, 2016).Google Scholar
Beilinson, A., ‘ p-adic periods and derived de Rham cohomology’, J. Amer. Math. Soc. 25(3) (2012), 715–738.Google Scholar
Berkovich, V. G., ‘On the comparison theorem for étale cohomology of non-Archimedean analytic spaces’, Israel J. Math. 92(1–3) (1995), 45–59.Google Scholar
Bosch, S., Lectures on Formal and Rigid Geometry, Lecture Notes in Mathematics, 2105 (Springer, Cham, 2014).Google Scholar
Colmez, P. and Nizioł, W., ‘Syntomic complexes and p-adic nearby cycles’, Invent. Math. 208(1) (2017), 1–108.Google Scholar
Diao, H., ‘Foundations of logarithmic adic spaces’, Preprint, 2017, arXiv:1709.05781.Google Scholar
Diao, H., Lan, K.-W., Liu, R. and Zhu, X., ‘Logarithmic Riemann–Hilbert correspondences for rigid varieties’, Preprint, 2018, arXiv:1803.05786.Google Scholar
de Jong, J. and van der Put, M., ‘étale cohomology of rigid analytic spaces’, Doc. Math. 1(01) (1996), 1–56.Google Scholar
Faltings, G., ‘ p-adic Hodge theory’, J. Amer. Math. Soc. 1(1) (1988), 255–299.Google Scholar
Fu, L., Etale Cohomology Theory, Nankai Tracts in Mathematics, 13 (World Scientific Publishing Co. Pte. Ltd, Hackensack, NJ, 2011).Google Scholar
Hansen, D., ‘Artin vanishing in rigid analytic geometry’, http://www.math.columbia.edu/%7Ehansen/artin.pdf, August 2017.Google Scholar
Huber, R., étale Cohomology of Rigid Analytic Varieties and Adic Spaces, Aspects of Mathematics, E30 (Friedr. Vieweg & Sohn, Braunschweig, 1996).Google Scholar
Kashiwara, Ma. and Schapira, P., Categories and Sheaves, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], 332 (Springer, Berlin, 2006).Google Scholar
Kiehl, R., ‘Die de Rham Kohomologie algebraischer Mannigfaltigkeiten über einem bewerteten Körper’, Publ. Math. Inst. Hautes Études Sci. 33 (1967), 5–20.Google Scholar
Lütkebohmert, W., ‘Riemann’s existence problem for a p-adic field’, Invent. Math. 111(2) (1993), 309–330.Google Scholar
Matsumura, H., Commutative Ring Theory, Cambridge Studies in Advanced Mathematics, 8 (Cambridge University Press, Cambridge, 1986), Translated from the Japanese by M. Reid.Google Scholar
Mitsui, K., ‘Criterion for minimality of rigid analytic surfaces’, http://www.math.kyoto-u.ac.jp/preprint/2009/20mitsui.pdf, 2009.Google Scholar
Olsson, M. C., ‘On faltings’ method of almost étale extensions’, inAlgebraic Geometry—Seattle 2005, Part 2, Proceedings of Symposia Pure Mathematics, 80 (American Mathematical Society, Providence, RI, 2009), 811–936.Google Scholar
Scholze, P., ‘Perfectoid spaces’, Publ. Math. Inst. Hautes Études Sci. 116 (2012), 245–313.Google Scholar
Scholze, P., ‘ p-adic Hodge theory for rigid-analytic varieties’, Forum Math. Pi 1 (2013), e1, 77.Google Scholar
Scholze, P., ‘Perfectoid spaces: a survey’, inCurrent Developments in Mathematics 2012 (International Press, Somerville, MA, 2013), 193–227.Google Scholar
Scholze, P., ‘ p-adic Hodge theory for rigid-analytic varieties—corrigendum [MR 3090230]’, Forum Math. Pi 4 (2016), e6, 4.Google Scholar
Tate, J. T., ‘ p-divisible groups’, inProc. Conf. Local Fields (Driebergen, 1966) (Springer, Berlin, 1967), 158–183.Google Scholar
Temkin, M., ‘Functorial desingularization over Q: boundaries and the embedded case’, Israel J. Math. (2018), doi:10.1007/s11856-018-1656-6.Google Scholar
Théorie des topos et cohomologie étale des schémas. Tome 2, Lecture Notes in Mathematics, 270, Springer-Verlag, Berlin–New York, 1972, Séminaire de Géométrie Algébrique du Bois-Marie 1963–1964 (SGA 4), Dirigé par M. Artin, A. Grothendieck et J. L. Verdier. Avec la collaboration de N. Bourbaki, P. Deligne et B. Saint-Donat.Google Scholar