Article contents
EISENSTEIN–KRONECKER SERIES VIA THE POINCARÉ BUNDLE
Published online by Cambridge University Press: 30 September 2019
Abstract
A classical construction of Katz gives a purely algebraic construction of Eisenstein–Kronecker series using the Gauß–Manin connection on the universal elliptic curve. This approach gives a systematic way to study algebraic and 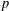 $p$-adic properties of real-analytic Eisenstein series. In the first part of this paper we provide an alternative algebraic construction of Eisenstein–Kronecker series via the Poincaré bundle. Building on this, we give in the second part a new conceptional construction of Katz’ two-variable
$p$-adic properties of real-analytic Eisenstein series. In the first part of this paper we provide an alternative algebraic construction of Eisenstein–Kronecker series via the Poincaré bundle. Building on this, we give in the second part a new conceptional construction of Katz’ two-variable 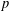 $p$-adic Eisenstein measure through
$p$-adic Eisenstein measure through 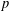 $p$-adic theta functions of the Poincaré bundle.
$p$-adic theta functions of the Poincaré bundle.
MSC classification
- Type
- Research Article
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author 2019
References
- 1
- Cited by




