Article contents
ANALYTIC EQUIVALENCE RELATIONS SATISFYING HYPERARITHMETIC-IS-RECURSIVE
Published online by Cambridge University Press: 27 April 2015
Abstract
We prove, in 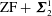 $\text{ZF}+\boldsymbol{{\it\Sigma}}_{2}^{1}$-determinacy, that, for any analytic equivalence relation
$\text{ZF}+\boldsymbol{{\it\Sigma}}_{2}^{1}$-determinacy, that, for any analytic equivalence relation 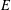 $E$, the following three statements are equivalent: (1)
$E$, the following three statements are equivalent: (1) 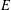 $E$ does not have perfectly many classes, (2)
$E$ does not have perfectly many classes, (2) 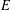 $E$ satisfies hyperarithmetic-is-recursive on a cone, and (3) relative to some oracle, for every equivalence class
$E$ satisfies hyperarithmetic-is-recursive on a cone, and (3) relative to some oracle, for every equivalence class 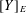 $[Y]_{E}$ we have that a real
$[Y]_{E}$ we have that a real 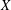 $X$ computes a member of the equivalence class if and only if
$X$ computes a member of the equivalence class if and only if 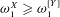 ${\it\omega}_{1}^{X}\geqslant {\it\omega}_{1}^{[Y]}$. We also show that the implication from (1) to (2) is equivalent to the existence of sharps over
${\it\omega}_{1}^{X}\geqslant {\it\omega}_{1}^{[Y]}$. We also show that the implication from (1) to (2) is equivalent to the existence of sharps over 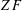 $ZF$.
$ZF$.
MSC classification
- Type
- Research Article
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/3.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author 2015
References
- 3
- Cited by





