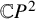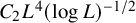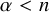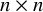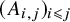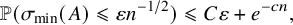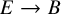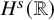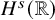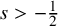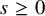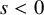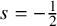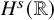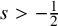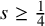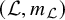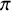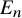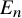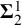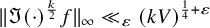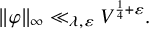Number Theory
Smith theory and cyclic base change functoriality
- Part of:
-
- Published online by Cambridge University Press:
- 15 January 2024, e1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Differential Geometry and Geometric Analysis
Degrees of maps and multiscale geometry
- Part of:
-
- Published online by Cambridge University Press:
- 18 January 2024, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Probability
The least singular value of a random symmetric matrix
- Part of:
-
- Published online by Cambridge University Press:
- 23 January 2024, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebraic and Complex Geometry
Virasoro Constraints for Toric Bundles
- Part of:
-
- Published online by Cambridge University Press:
- 01 January 2024, e4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Corrigendum
On local Galois deformation rings – CORRIGENDUM
-
- Published online by Cambridge University Press:
- 26 February 2024, e5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Differential Equations
Sharp well-posedness for the cubic NLS and mKdV in
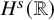 $H^s({{\mathbb {R}}})$
$H^s({{\mathbb {R}}})$
- Part of:
-
- Published online by Cambridge University Press:
- 02 April 2024, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dynamics
On the ergodic theory of the real Rel foliation
- Part of:
-
- Published online by Cambridge University Press:
- 02 April 2024, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Topology
The Chromatic Fourier Transform
- Part of:
-
- Published online by Cambridge University Press:
- 08 April 2024, e8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebraic and Complex Geometry
Logarithmic Donaldson–Thomas theory
- Part of:
-
- Published online by Cambridge University Press:
- 18 April 2024, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Foundations
ON HOMOMORPHISM GRAPHS
- Part of:
-
- Published online by Cambridge University Press:
- 13 May 2024, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Number Theory
Theta functions, fourth moments of eigenforms and the sup-norm problem II
- Part of:
-
- Published online by Cambridge University Press:
- 30 May 2024, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation