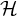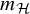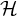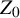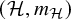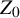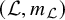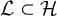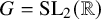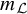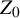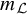1. Introduction
Let
![]() ${{\mathcal {H}}}$
be a stratum of area-one translation surfaces, and let
${{\mathcal {H}}}$
be a stratum of area-one translation surfaces, and let
![]() $G {\, \stackrel {\mathrm {def}}{=}\, } \operatorname {SL}_2({\mathbb {R}})$
. There is a G-invariant finite measure
$G {\, \stackrel {\mathrm {def}}{=}\, } \operatorname {SL}_2({\mathbb {R}})$
. There is a G-invariant finite measure
![]() $m_{{{\mathcal {H}}}}$
on
$m_{{{\mathcal {H}}}}$
on
![]() ${{\mathcal {H}}}$
known as the Masur-Veech measure, and the dynamics of the G-action on
${{\mathcal {H}}}$
known as the Masur-Veech measure, and the dynamics of the G-action on
![]() $({{\mathcal {H}}}, m_{{{\mathcal {H}}}})$
have been intensively studied in recent years and are intimately connected to many problems in geometry and ergodic theory; see, for example, [Reference Masur and TabachnikovMaTa, Reference Zorich, Cartier, Julia, Moussa and VanhoveZo]. Suppose that surfaces in
$({{\mathcal {H}}}, m_{{{\mathcal {H}}}})$
have been intensively studied in recent years and are intimately connected to many problems in geometry and ergodic theory; see, for example, [Reference Masur and TabachnikovMaTa, Reference Zorich, Cartier, Julia, Moussa and VanhoveZo]. Suppose that surfaces in
![]() ${{\mathcal {H}}}$
have k singularities, where
${{\mathcal {H}}}$
have k singularities, where
![]() $k\geq 2$
. Then there is a
$k\geq 2$
. Then there is a
![]() $k-1$
-dimensional foliation of
$k-1$
-dimensional foliation of
![]() ${{\mathcal {H}}}$
, known as the real Rel foliation. A precise definition of the foliation and some of its properties will be given below in §2.2. Loosely speaking, two surfaces are in the same real Rel leaf if one can be obtained from the other by a surgery in which singular points are moved with respect to each other in the horizontal direction without otherwise changing the geometry of the surface. A natural question, which we address here, is the ergodic properties of this foliation. Most of our results below rely on an unpublished result of Brown, Eskin, Filip and Rodriguez-Hertz, which we refer to as Statement A and discuss in §5.
${{\mathcal {H}}}$
, known as the real Rel foliation. A precise definition of the foliation and some of its properties will be given below in §2.2. Loosely speaking, two surfaces are in the same real Rel leaf if one can be obtained from the other by a surgery in which singular points are moved with respect to each other in the horizontal direction without otherwise changing the geometry of the surface. A natural question, which we address here, is the ergodic properties of this foliation. Most of our results below rely on an unpublished result of Brown, Eskin, Filip and Rodriguez-Hertz, which we refer to as Statement A and discuss in §5.
As we review in §2.2, by labeling the singularities and removing a set of leaves of measure zero, we can think of the real Rel leaves as being the orbits of an action of a group Z on
![]() ${{\mathcal {H}}}$
, where
${{\mathcal {H}}}$
, where
![]() $Z \cong {\mathbb {R}}^{k-1}$
, and the restriction of this action to any one-dimensional subgroup of Z defines a flow. Our first main result is the following.
$Z \cong {\mathbb {R}}^{k-1}$
, and the restriction of this action to any one-dimensional subgroup of Z defines a flow. Our first main result is the following.
Theorem 1.1. Assume Statement A. Let
![]() ${{\mathcal {H}}}$
be a connected component of a stratum
${{\mathcal {H}}}$
be a connected component of a stratum
![]() ${{\mathcal {H}}}(a_1, \ldots , a_k)$
with all
${{\mathcal {H}}}(a_1, \ldots , a_k)$
with all
![]() $a_i>0$
(i.e., no marked points). Let
$a_i>0$
(i.e., no marked points). Let
![]() $m_{{\mathcal {H}}}$
be the Masur-Veech measure on
$m_{{\mathcal {H}}}$
be the Masur-Veech measure on
![]() ${{\mathcal {H}}}$
, let
${{\mathcal {H}}}$
, let
![]() $Z \cong {\mathbb {R}}^{k-1}$
be the corresponding action given by translation along the leaves of the real Rel foliation, and let
$Z \cong {\mathbb {R}}^{k-1}$
be the corresponding action given by translation along the leaves of the real Rel foliation, and let
![]() $Z_0 \subset Z$
be any one-dimensional connected subgroup of Z. Then the
$Z_0 \subset Z$
be any one-dimensional connected subgroup of Z. Then the
![]() $Z_0$
-flow on
$Z_0$
-flow on
![]() $({{\mathcal {H}}}, m_{{{\mathcal {H}}}})$
is mixing of all orders (and in particular, ergodic).
$({{\mathcal {H}}}, m_{{{\mathcal {H}}}})$
is mixing of all orders (and in particular, ergodic).
The definition of mixing of all orders is given in §3.3. For purposes of this introduction, it is enough to note that it implies ergodicity of any nontrivial element. Note that when
![]() ${{\mathcal {H}}}$
has marked points, there will be subgroups
${{\mathcal {H}}}$
has marked points, there will be subgroups
![]() $Z_0$
which only move the marked points on surfaces without otherwise changing the geometry, and the conclusion of Theorem 1.1 will not hold. This is the only obstruction to generalizing our results to strata with marked points; see Theorem 8.1.
$Z_0$
which only move the marked points on surfaces without otherwise changing the geometry, and the conclusion of Theorem 1.1 will not hold. This is the only obstruction to generalizing our results to strata with marked points; see Theorem 8.1.
The proof of Theorem 1.1, as well as most of the other results of this paper, relies crucially on measure-rigidity results of Eskin, Mirzakhani and Mohammadi [Reference Eskin and MirzakhaniEM, Reference Eskin, Mirzakhani and MohammadiEMM] and further forthcoming work extending these results, which we will describe in §5.
Theorem 1.1 improves on the results of several authors. In those results, ergodicity for the full Rel foliation was studied. The full Rel foliation (also referred to as the ‘kernel foliation’, ‘isoperiodic foliation’ or ‘absolute period foliation’) will also be defined in §2.2. Its leaves are of dimension
![]() $2(k-1)$
– that is, twice the dimension of the real Rel leaves. Loosely speaking, two surfaces are in the same leaf for this foliation if one can be obtained from the other by moving the singularities (without otherwise affecting the geometry of the surface). That is, we relax the hypothesis that points can only be moved horizontally. The first ergodicity results for the full Rel foliation were obtained by McMullen [Reference McMullenMcM], who proved ergodicity in the two strata
$2(k-1)$
– that is, twice the dimension of the real Rel leaves. Loosely speaking, two surfaces are in the same leaf for this foliation if one can be obtained from the other by moving the singularities (without otherwise affecting the geometry of the surface). That is, we relax the hypothesis that points can only be moved horizontally. The first ergodicity results for the full Rel foliation were obtained by McMullen [Reference McMullenMcM], who proved ergodicity in the two strata
![]() ${{\mathcal {H}}}(1,1)$
and
${{\mathcal {H}}}(1,1)$
and
![]() ${{\mathcal {H}}}(1,1,1,1)$
. Subsequently, Calsamiglia, Deroin and Francaviglia [Reference Calsamiglia, Deroin and FrancavigliaCDF] proved ergodicity in all principal strata, and Hamenstädt [Reference HamenstädtHam] reproved their result by a simpler argument. Recently, Winsor [Reference WinsorWi1] proved ergodicity for most of the additional strata and, in [Reference WinsorWi2], showed that there are dense orbits for the
${{\mathcal {H}}}(1,1,1,1)$
. Subsequently, Calsamiglia, Deroin and Francaviglia [Reference Calsamiglia, Deroin and FrancavigliaCDF] proved ergodicity in all principal strata, and Hamenstädt [Reference HamenstädtHam] reproved their result by a simpler argument. Recently, Winsor [Reference WinsorWi1] proved ergodicity for most of the additional strata and, in [Reference WinsorWi2], showed that there are dense orbits for the
![]() $Z_0$
-flow, for any
$Z_0$
-flow, for any
![]() $Z_0$
as in Theorem 1.1. Note that ergodicity for a foliation is implied by ergodicity for any of its subfoliations, and that ergodicity implies the existence of dense leaves, and thus Theorem 1.1 generalizes all of these results. Also note that full Rel is a foliation which is not given by a group action, and the notions of mixing and multiple mixing do not make sense in this case.
$Z_0$
as in Theorem 1.1. Note that ergodicity for a foliation is implied by ergodicity for any of its subfoliations, and that ergodicity implies the existence of dense leaves, and thus Theorem 1.1 generalizes all of these results. Also note that full Rel is a foliation which is not given by a group action, and the notions of mixing and multiple mixing do not make sense in this case.
The papers [Reference McMullenMcM, Reference Calsamiglia, Deroin and FrancavigliaCDF] go beyond ergodicity and obtain classifications of full Rel closed leaves and leaf-closures in their respective settings. We suspect that there is not a reasonable classification of real Rel leaf-closures; indeed, it is already known (see [Reference Hooper and WeissHW]) that there are real Rel trajectories that leave every compact set never to return.
The strata
![]() ${{\mathcal {H}}}$
support other interesting measures for which similar questions could be asked. Namely, by work of Eskin, Mirzakhani and Mohammadi [Reference Eskin and MirzakhaniEM, Reference Eskin, Mirzakhani and MohammadiEMM], for any
${{\mathcal {H}}}$
support other interesting measures for which similar questions could be asked. Namely, by work of Eskin, Mirzakhani and Mohammadi [Reference Eskin and MirzakhaniEM, Reference Eskin, Mirzakhani and MohammadiEMM], for any
![]() $q \in {{\mathcal {H}}}$
, the orbit-closure
$q \in {{\mathcal {H}}}$
, the orbit-closure
![]() ${{\mathcal L}} {\, \stackrel {\mathrm {def}}{=}\, } \overline {Gq}$
is the support of a unique smooth G-invariant measure which we denote by
${{\mathcal L}} {\, \stackrel {\mathrm {def}}{=}\, } \overline {Gq}$
is the support of a unique smooth G-invariant measure which we denote by
![]() $m_{{{\mathcal L}}}$
. Let
$m_{{{\mathcal L}}}$
. Let
![]() $Z_{{{\mathcal L}}}$
be the subgroup of Z leaving
$Z_{{{\mathcal L}}}$
be the subgroup of Z leaving
![]() ${{\mathcal L}}$
invariant. Then
${{\mathcal L}}$
invariant. Then
![]() $Z_{{{\mathcal L}}}$
also preserves
$Z_{{{\mathcal L}}}$
also preserves
![]() $m_{{{\mathcal L}}}$
and for many choices of
$m_{{{\mathcal L}}}$
and for many choices of
![]() ${{\mathcal L}}$
, we have
${{\mathcal L}}$
, we have
![]() $\dim Z_{{\mathcal L}}>0$
. In these cases, for any closed connected
$\dim Z_{{\mathcal L}}>0$
. In these cases, for any closed connected
![]() $Z_1 \subset Z_{{{\mathcal L}}}$
, there is a complexification
$Z_1 \subset Z_{{{\mathcal L}}}$
, there is a complexification
![]() $\mathfrak {R}_{1}$
, which gives a foliation of
$\mathfrak {R}_{1}$
, which gives a foliation of
![]() ${{\mathcal L}}$
whose leaves
${{\mathcal L}}$
whose leaves
![]() $\mathfrak {R}_{1}(q)$
have dimension
$\mathfrak {R}_{1}(q)$
have dimension
![]() $2 \dim Z_1$
(see §2.2). The leaves
$2 \dim Z_1$
(see §2.2). The leaves
![]() $\mathfrak {R}_1(q)$
have a natural translation structure, and this induces a natural locally finite translation-invariant measure on each leaf. With this terminology, we can now state the main result of this paper:
$\mathfrak {R}_1(q)$
have a natural translation structure, and this induces a natural locally finite translation-invariant measure on each leaf. With this terminology, we can now state the main result of this paper:
Theorem 1.2. Assume Statement A. Let
![]() ${{\mathcal L}}$
be a G-orbit closure, and let
${{\mathcal L}}$
be a G-orbit closure, and let
![]() $m_{\mathcal {L}}, \, Z_{{{\mathcal L}}} $
be as above, where
$m_{\mathcal {L}}, \, Z_{{{\mathcal L}}} $
be as above, where
![]() $\dim Z_{{{\mathcal L}}}>0$
. Let
$\dim Z_{{{\mathcal L}}}>0$
. Let
![]() $z_0$
be a nontrivial element of
$z_0$
be a nontrivial element of
![]() $Z_{{{\mathcal L}}}$
, and let
$Z_{{{\mathcal L}}}$
, and let
![]() $Z_0 = \mathrm {span}_{{\mathbb {R}}} (z_0).$
Then either
$Z_0 = \mathrm {span}_{{\mathbb {R}}} (z_0).$
Then either
-
(1) The action of
 $Z_0$
on
$Z_0$
on
 $\left ({{\mathcal L}}, m_{\mathcal {L}} \right )$
is mixing of all orders (and in particular,
$\left ({{\mathcal L}}, m_{\mathcal {L}} \right )$
is mixing of all orders (and in particular,
 $z_0$
acts ergodically); or
$z_0$
acts ergodically); or -
(2) there is an intermediate closed connected subgroup
 $Z_1$
so that
$Z_1$
so that
 $Z_0\subset Z_1\subset Z_{{{\mathcal L}}}$
, and the complexification
$Z_0\subset Z_1\subset Z_{{{\mathcal L}}}$
, and the complexification
 $\mathfrak {R}_1$
of
$\mathfrak {R}_1$
of
 $Z_1$
satisfies
$Z_1$
satisfies-
• for every
 $q \in {{\mathcal L}}$
, the leaf
$q \in {{\mathcal L}}$
, the leaf
 $\mathfrak {R}_1(q)$
is closed, and
$\mathfrak {R}_1(q)$
is closed, and -
• for
 $m_{\mathcal {L}}$
-a.e. q,
$m_{\mathcal {L}}$
-a.e. q,
 $\mathfrak {R}_1(q)$
is of finite volume with respect to its translation-invariant measure, and
$\mathfrak {R}_1(q)$
is of finite volume with respect to its translation-invariant measure, and
 $\overline {Z_0q}=\mathfrak {R}_1(q)$
.
$\overline {Z_0q}=\mathfrak {R}_1(q)$
.
-
Example 1.3 (Branched covers).
Using covering constructions, it is not hard to find examples for which Case (2) above holds. Namely, suppose
![]() ${\mathcal {H}} = {\mathcal {H}}(a_1, \ldots , a_k)$
is a connected component of a stratum and
${\mathcal {H}} = {\mathcal {H}}(a_1, \ldots , a_k)$
is a connected component of a stratum and
![]() ${\mathcal {H}}' = {\mathcal {H}}(a_1, \ldots , a_k, 0)$
is the space obtained from
${\mathcal {H}}' = {\mathcal {H}}(a_1, \ldots , a_k, 0)$
is the space obtained from
![]() ${\mathcal {H}}$
by marking an additional nonsingular point on every surface in
${\mathcal {H}}$
by marking an additional nonsingular point on every surface in
![]() ${\mathcal {H}}$
. Thus, we can write every surface in
${\mathcal {H}}$
. Thus, we can write every surface in
![]() ${\mathcal {H}}'$
as a pair
${\mathcal {H}}'$
as a pair
![]() $(q, p)$
, where
$(q, p)$
, where
![]() $q \in {\mathcal {H}}$
and p is a nonsingular point on the underlying surface
$q \in {\mathcal {H}}$
and p is a nonsingular point on the underlying surface
![]() $M_q$
. We let
$M_q$
. We let
![]() ${{\mathcal L}}$
be the Hurwitz space of all surfaces obtained as branched covers of
${{\mathcal L}}$
be the Hurwitz space of all surfaces obtained as branched covers of
![]() $M_q$
a fixed topolgicial type, branched only over p, for surfaces
$M_q$
a fixed topolgicial type, branched only over p, for surfaces
![]() $(q,p) \in {\mathcal {H}}'$
, and let
$(q,p) \in {\mathcal {H}}'$
, and let
![]() $Z_0$
be the subspace of
$Z_0$
be the subspace of
![]() $Z_{{{\mathcal L}}}$
consisting of deformations which move p horizontally on
$Z_{{{\mathcal L}}}$
consisting of deformations which move p horizontally on
![]() $M_q$
relative to the other singular points, without affecting the periods of paths between other singular points. In this case, we have
$M_q$
relative to the other singular points, without affecting the periods of paths between other singular points. In this case, we have
![]() $Z_0 = Z_1$
,
$Z_0 = Z_1$
,
![]() $\mathfrak {R}_1(q)$
is naturally isomorphic to
$\mathfrak {R}_1(q)$
is naturally isomorphic to
![]() $M_q$
, with singular points removed, the translation invariant measure on
$M_q$
, with singular points removed, the translation invariant measure on
![]() $\mathfrak {R}_1(q)$
is the natural measure on
$\mathfrak {R}_1(q)$
is the natural measure on
![]() $M_q$
, and we will have
$M_q$
, and we will have
![]() $\mathfrak {R}_1(q) = \overline {Z_0q}$
whenever the horizontal direction is minimal on
$\mathfrak {R}_1(q) = \overline {Z_0q}$
whenever the horizontal direction is minimal on
![]() $M_q$
.
$M_q$
.
By Theorem 1.2, in order to establish ergodicity of real Rel subfoliations on G-orbit-closures, it is enough to rule out Case (2). We will prove Proposition 7.1, which provides a simple way to achieve this, using cylinder circumferences of surfaces in
![]() ${{\mathcal L}}$
. Theorems 1.1 and 8.1 are deduced from Theorem 1.2 using Proposition 7.1.
${{\mathcal L}}$
. Theorems 1.1 and 8.1 are deduced from Theorem 1.2 using Proposition 7.1.
The following statement is an immediate consequence of Theorem 1.2.
Corollary 1.4. Assume Statement A. Let
![]() ${{\mathcal L}}$
be a G-orbit-closure, let
${{\mathcal L}}$
be a G-orbit-closure, let
![]() $m_{{{\mathcal L}}}, Z_{{{\mathcal L}}}$
be as above, and let
$m_{{{\mathcal L}}}, Z_{{{\mathcal L}}}$
be as above, and let
![]() $Z_1 \subset Z_{{{\mathcal L}}}$
be one-dimensional. Suppose that the foliation induced by the complexification
$Z_1 \subset Z_{{{\mathcal L}}}$
be one-dimensional. Suppose that the foliation induced by the complexification
![]() $\mathfrak {R}_1$
has a dense leaf. Then the
$\mathfrak {R}_1$
has a dense leaf. Then the
![]() $Z_1$
-flow on
$Z_1$
-flow on
![]() $({{\mathcal L}}, m_{{{\mathcal L}}})$
is mixing of all orders (and in particular, ergodic).
$({{\mathcal L}}, m_{{{\mathcal L}}})$
is mixing of all orders (and in particular, ergodic).
The density of certain leaves of the full Rel foliation in G-orbit-closures of rank one was obtained by Ygouf in [Reference YgoufY]. Using these results, we obtain ergodicity of one-dimensional subgroups of the real Rel foliation in many cases. For instance, using [Reference YgoufY, Thm. A & Prop. 5.1], we have the following:
Corollary 1.5. Assume Statement A. The real Rel foliation is mixing of all orders (and in particular, ergodic) in any eigenform locus in
![]() ${{\mathcal {H}}}(1,1)$
with a non-square discriminant.
${{\mathcal {H}}}(1,1)$
with a non-square discriminant.
Recall that in [Reference WinsorWi2] Winsor proved the existence of dense real Rel leaves, and dense leaves for one-dimensional flows
![]() $Z_0$
, in all strata. Using these results in conjunction with Corollary 1.4, one can obtain an alternative proof of Theorem 1.1 that avoids the use of Proposition 7.1.
$Z_0$
, in all strata. Using these results in conjunction with Corollary 1.4, one can obtain an alternative proof of Theorem 1.1 that avoids the use of Proposition 7.1.
We also consider the entropy of real-Rel flows and show the following:
Theorem 1.6. Let
![]() ${{\mathcal L}}, m_{{{\mathcal L}}}, Z_{{{\mathcal L}}}, z_0$
be as in the statement of Theorem 1.2. Then the entropy of the action of
${{\mathcal L}}, m_{{{\mathcal L}}}, Z_{{{\mathcal L}}}, z_0$
be as in the statement of Theorem 1.2. Then the entropy of the action of
![]() $\mathrm {Rel}_{z_0}$
on the measure space
$\mathrm {Rel}_{z_0}$
on the measure space
![]() $({{\mathcal L}}, m_{{{\mathcal L}}})$
is zero.
$({{\mathcal L}}, m_{{{\mathcal L}}})$
is zero.
Using the geodesic flow, one easily shows that
![]() $\mathrm {Rel}_{z_0}$
is conjugate to
$\mathrm {Rel}_{z_0}$
is conjugate to
![]() $\mathrm {Rel}_{tz_0}$
for any
$\mathrm {Rel}_{tz_0}$
for any
![]() $t>0$
, and from this, it follows that the entropy is either zero or infinite. However, the Rel flow is not continuous, and we could not find a simple way to rule out infinite entropy. Our proof gives a more general result; see Theorem 9.1. However, the argument fails for
$t>0$
, and from this, it follows that the entropy is either zero or infinite. However, the Rel flow is not continuous, and we could not find a simple way to rule out infinite entropy. Our proof gives a more general result; see Theorem 9.1. However, the argument fails for
![]() $Z_0$
-invariant measures for which the backward time geodesic flow diverges almost surely, and thus, we do not settle the question of whether the topological entropy of real Rel flows is zero.
$Z_0$
-invariant measures for which the backward time geodesic flow diverges almost surely, and thus, we do not settle the question of whether the topological entropy of real Rel flows is zero.
1.1. Outline
In §2, we give background material on translation surfaces, their moduli spaces, and the Rel foliation. In §3, we use standard facts about joinings to build a measure
![]() $\theta $
on the product of two strata (see (3.1)), depending on a real Rel flow
$\theta $
on the product of two strata (see (3.1)), depending on a real Rel flow
![]() $Z_0$
, such that if
$Z_0$
, such that if
![]() $\theta $
is the product measure, then
$\theta $
is the product measure, then
![]() $Z_0$
is ergodic. In §3.3, we discuss a technique of Mozes that makes it possible to upgrade ergodicity to mixing of all orders. In §4, we show that
$Z_0$
is ergodic. In §3.3, we discuss a technique of Mozes that makes it possible to upgrade ergodicity to mixing of all orders. In §4, we show that
![]() $\theta $
is ergodic for the diagonal action of the upper triangular group
$\theta $
is ergodic for the diagonal action of the upper triangular group
![]() $P \subset G$
on the product of two strata. In §5, we state Statement A, which is a far-reaching measure rigidity result of Brown, Eskin, Filip and Rodriguez-Hertz for P-ergodic measures on products of two strata. In §6, we use Statement A, as well as prior results for the action on one stratum due to Wright, in order to characterize the situations in which
$P \subset G$
on the product of two strata. In §5, we state Statement A, which is a far-reaching measure rigidity result of Brown, Eskin, Filip and Rodriguez-Hertz for P-ergodic measures on products of two strata. In §6, we use Statement A, as well as prior results for the action on one stratum due to Wright, in order to characterize the situations in which
![]() $\theta $
is not a product measure, thus proving Theorem 1.2. Proposition 7.1 is proved in §7, and we check its conditions to deduce Theorems 1.1 and 8.1 in §8. We prove Theorem 1.6 in §9.
$\theta $
is not a product measure, thus proving Theorem 1.2. Proposition 7.1 is proved in §7, and we check its conditions to deduce Theorems 1.1 and 8.1 in §8. We prove Theorem 1.6 in §9.
2. Preliminaries about translation surfaces
2.1. Strata, period coordinates
In this section, we collect standard facts about translation surfaces and fix our notation. For more details, we refer the reader to [Reference Zorich, Cartier, Julia, Moussa and VanhoveZo, Reference WrightWr1, Reference Bainbridge, Smillie and WeissBSW]. Below, we briefly summarize the treatment in [Reference Bainbridge, Smillie and WeissBSW, §2].
Let S be a compact oriented surface of genus g,
![]() $\Sigma = \{\xi _1, \ldots , \xi _k \} \subset S$
a finite set,
$\Sigma = \{\xi _1, \ldots , \xi _k \} \subset S$
a finite set,
![]() $a_1, \ldots , a_k$
non-negative integers with
$a_1, \ldots , a_k$
non-negative integers with
![]() $\sum a_i = 2g-2$
, and
$\sum a_i = 2g-2$
, and
![]() ${{\mathcal {H}}} = {{\mathcal {H}}}(a_1, \ldots , a_k)$
the corresponding stratum of unit-area translation surfaces. We let
${{\mathcal {H}}} = {{\mathcal {H}}}(a_1, \ldots , a_k)$
the corresponding stratum of unit-area translation surfaces. We let
![]() ${{\mathcal {H}}}_{\mathrm {m}}={{\mathcal {H}}}_{\mathrm {m}}(a_1, \ldots , a_k)$
denote the stratum of unit-area marked translation surfaces and
${{\mathcal {H}}}_{\mathrm {m}}={{\mathcal {H}}}_{\mathrm {m}}(a_1, \ldots , a_k)$
denote the stratum of unit-area marked translation surfaces and
![]() $\pi : {{\mathcal {H}}}_{\mathrm {m}} \to {{\mathcal {H}}}$
the forgetful mapping. Our convention is that singular points are labeled, or equivalently,
$\pi : {{\mathcal {H}}}_{\mathrm {m}} \to {{\mathcal {H}}}$
the forgetful mapping. Our convention is that singular points are labeled, or equivalently,
![]() ${{\mathcal {H}}} = {{\mathcal {H}}}_{\mathrm {m}} / \operatorname {Mod}(S, \Sigma )$
, where
${{\mathcal {H}}} = {{\mathcal {H}}}_{\mathrm {m}} / \operatorname {Mod}(S, \Sigma )$
, where
![]() $\operatorname {Mod}(S, \Sigma )$
is the group of isotopy classes of orientation-preserving homeomorphisms of S fixing
$\operatorname {Mod}(S, \Sigma )$
is the group of isotopy classes of orientation-preserving homeomorphisms of S fixing
![]() $\Sigma $
, up to an isotopy fixing
$\Sigma $
, up to an isotopy fixing
![]() $\Sigma $
.
$\Sigma $
.
There is an
![]() ${\mathbb {R}}_{>0}$
-action that dilates the atlas of a translation surface by
${\mathbb {R}}_{>0}$
-action that dilates the atlas of a translation surface by
![]() $ c\in {\mathbb {R}}_{>0}$
. For a stratum
$ c\in {\mathbb {R}}_{>0}$
. For a stratum
![]() ${\mathcal {H}}$
and marked stratum
${\mathcal {H}}$
and marked stratum
![]() ${\mathcal {H}}_{\mathrm {m}}$
, we denote the collection of surfaces of arbitrary area, obtained by applying such dilations, by
${\mathcal {H}}_{\mathrm {m}}$
, we denote the collection of surfaces of arbitrary area, obtained by applying such dilations, by
![]() $\bar {{\mathcal {H}}}, \, \bar {{\mathcal {H}}}_{\mathrm {m}}$
. The marked stratum
$\bar {{\mathcal {H}}}, \, \bar {{\mathcal {H}}}_{\mathrm {m}}$
. The marked stratum
![]() $\bar {{\mathcal {H}}}_{\mathrm {m}}$
is a linear manifold modeled on the vector space
$\bar {{\mathcal {H}}}_{\mathrm {m}}$
is a linear manifold modeled on the vector space
![]() $H^1(S, \Sigma; {\mathbb {R}}^2)$
. It has a developing map
$H^1(S, \Sigma; {\mathbb {R}}^2)$
. It has a developing map
![]() $\mathrm {dev}: \bar {{\mathcal {H}}}_{\mathrm {m}} \to H^1(S, \Sigma; {\mathbb {R}}^2)$
, sending an element of
$\mathrm {dev}: \bar {{\mathcal {H}}}_{\mathrm {m}} \to H^1(S, \Sigma; {\mathbb {R}}^2)$
, sending an element of
![]() $\bar {{\mathcal {H}}}_{\mathrm {m}}$
represented by
$\bar {{\mathcal {H}}}_{\mathrm {m}}$
represented by
![]() $f: S \to M$
, where M is a translation surface, to
$f: S \to M$
, where M is a translation surface, to
![]() $f^*(\mathrm {hol}(M, \cdot ))$
, where for an oriented path
$f^*(\mathrm {hol}(M, \cdot ))$
, where for an oriented path
![]() $\gamma $
in M which is either closed or has endpoints at singularities,
$\gamma $
in M which is either closed or has endpoints at singularities,
 $\mathrm {hol}(M, \gamma ) = \left (\begin {matrix} \int _\gamma dx\\[3.5pt] \int _\gamma dy\end {matrix} \right )$
, and
$\mathrm {hol}(M, \gamma ) = \left (\begin {matrix} \int _\gamma dx\\[3.5pt] \int _\gamma dy\end {matrix} \right )$
, and
![]() $dx, dy$
are the 1-forms on M inherited from the plane. Furthermore, there is an open cover
$dx, dy$
are the 1-forms on M inherited from the plane. Furthermore, there is an open cover
![]() $\{\mathcal {U}_\tau \}$
of
$\{\mathcal {U}_\tau \}$
of
![]() ${{\mathcal {H}}}_{\mathrm {m}}$
, indexed by triangulations
${{\mathcal {H}}}_{\mathrm {m}}$
, indexed by triangulations
![]() $\tau $
of S with triangles whose vertices are in
$\tau $
of S with triangles whose vertices are in
![]() $\Sigma $
, and maps
$\Sigma $
, and maps
![]() $\mathrm {dev}|_{\mathcal {U}_\tau }: \mathcal {U}_{\tau } \to H^1(S, \Sigma; {\mathbb {R}}^2)$
, which are homeomorphisms onto their image, and such that the transition maps on overlaps for this atlas are restrictions of linear automorphisms of
$\mathrm {dev}|_{\mathcal {U}_\tau }: \mathcal {U}_{\tau } \to H^1(S, \Sigma; {\mathbb {R}}^2)$
, which are homeomorphisms onto their image, and such that the transition maps on overlaps for this atlas are restrictions of linear automorphisms of
![]() $H^1(S, \Sigma; {\mathbb {R}}^2)$
.
$H^1(S, \Sigma; {\mathbb {R}}^2)$
.
This atlas of charts
![]() $\{(\mathcal {U}_\tau , \mathrm {dev}|_{\mathcal {U}_\tau })\}$
is known as period coordinates. Since each
$\{(\mathcal {U}_\tau , \mathrm {dev}|_{\mathcal {U}_\tau })\}$
is known as period coordinates. Since each
![]() $\mathcal {U}_\tau $
is identified via period coordinates with an open subset of the vector space
$\mathcal {U}_\tau $
is identified via period coordinates with an open subset of the vector space
![]() $H^1(S, \Sigma; {\mathbb {R}}^2)$
, the tangent space at each
$H^1(S, \Sigma; {\mathbb {R}}^2)$
, the tangent space at each
![]() $\mathcal {U}_\tau $
is identified canonically with
$\mathcal {U}_\tau $
is identified canonically with
![]() $H^1(S, \Sigma; {\mathbb {R}}^2)$
, and thus the tangent bundle of
$H^1(S, \Sigma; {\mathbb {R}}^2)$
, and thus the tangent bundle of
![]() ${{\mathcal {H}}}_{\mathrm {m}}$
is locally constant. A sub-bundle of the tangent bundle is called locally constant or flat if it is constant in the charts afforded by period coordinates. The
${{\mathcal {H}}}_{\mathrm {m}}$
is locally constant. A sub-bundle of the tangent bundle is called locally constant or flat if it is constant in the charts afforded by period coordinates. The
![]() $\operatorname {Mod}(S, \Sigma )$
-action on
$\operatorname {Mod}(S, \Sigma )$
-action on
![]() ${{\mathcal {H}}}_{\mathrm {m}}$
is properly discontinuous, and hence,
${{\mathcal {H}}}_{\mathrm {m}}$
is properly discontinuous, and hence,
![]() ${{\mathcal {H}}}$
is an orbifold, and the map
${{\mathcal {H}}}$
is an orbifold, and the map
![]() $\pi : {{\mathcal {H}}}_{\mathrm {m}} \to {{\mathcal {H}}}$
is an orbifold covering map.
$\pi : {{\mathcal {H}}}_{\mathrm {m}} \to {{\mathcal {H}}}$
is an orbifold covering map.
The group G acts on translation surfaces in
![]() ${{\mathcal {H}}}$
by modifying planar charts and acts on
${{\mathcal {H}}}$
by modifying planar charts and acts on
![]() $H^1(S, \Sigma; {\mathbb {R}}^2)$
via its action on
$H^1(S, \Sigma; {\mathbb {R}}^2)$
via its action on
![]() ${\mathbb {R}}^2$
, thus inducing a G-action on
${\mathbb {R}}^2$
, thus inducing a G-action on
![]() ${{\mathcal {H}}}_{\mathrm {m}}$
. The G-action commutes with the
${{\mathcal {H}}}_{\mathrm {m}}$
. The G-action commutes with the
![]() $\operatorname {Mod}(S, \Sigma )$
-action, and thus, the map
$\operatorname {Mod}(S, \Sigma )$
-action, and thus, the map
![]() $\pi $
is G-equivariant for these actions. The G-action on
$\pi $
is G-equivariant for these actions. The G-action on
![]() ${{\mathcal {H}}}_{\mathrm {m}}$
is free since
${{\mathcal {H}}}_{\mathrm {m}}$
is free since
![]() $\mathrm {dev}(g\mathbf {q}) \neq \mathrm {dev}(\mathbf {q})$
for any nontrivial
$\mathrm {dev}(g\mathbf {q}) \neq \mathrm {dev}(\mathbf {q})$
for any nontrivial
![]() $g \in G$
. We will use the following subgroups of G:
$g \in G$
. We will use the following subgroups of G:
 $$ \begin{align*} g_t = \left( \begin{matrix} e^t & 0 \\ 0 & e^{-t}\end{matrix} \right), \ \ \ u_s = & \left( \begin{matrix} 1 & s \\ 0 & 1\end{matrix} \right) \\ U = \{u_s : s \in {\mathbb{R}}\}, \ \ \ P = & \left\{ \left( \begin{matrix} a & b \\ 0 & a^{-1} \end{matrix} \right): a> 0, \ b \in {\mathbb{R}}\right\}. \end{align*} $$
$$ \begin{align*} g_t = \left( \begin{matrix} e^t & 0 \\ 0 & e^{-t}\end{matrix} \right), \ \ \ u_s = & \left( \begin{matrix} 1 & s \\ 0 & 1\end{matrix} \right) \\ U = \{u_s : s \in {\mathbb{R}}\}, \ \ \ P = & \left\{ \left( \begin{matrix} a & b \\ 0 & a^{-1} \end{matrix} \right): a> 0, \ b \in {\mathbb{R}}\right\}. \end{align*} $$
2.2. Rel foliation and real Rel foliation
We define and list some important properties of the Rel foliation, the real Rel foliation and the corresponding action on the space of surfaces without horizontal saddle connections. See [Reference Minsky and WeissMW, Reference Bainbridge, Smillie and WeissBSW] for more details. See also [Reference Zorich, Cartier, Julia, Moussa and VanhoveZo, Reference McMullenMcM], and references therein.
We have a canonical splitting
![]() ${\mathbb {R}}^2 = {\mathbb {R}} \oplus {\mathbb {R}}$
, and we write
${\mathbb {R}}^2 = {\mathbb {R}} \oplus {\mathbb {R}}$
, and we write
![]() ${\mathbb {R}}^2 = {\mathbb {R}}_{\mathrm {x}} \oplus {\mathbb {R}}_{\mathrm {y}}$
to distinguish the two summands in this splitting. There is a corresponding splitting
${\mathbb {R}}^2 = {\mathbb {R}}_{\mathrm {x}} \oplus {\mathbb {R}}_{\mathrm {y}}$
to distinguish the two summands in this splitting. There is a corresponding splitting
We also have a canonical restriction map
![]() ${\mathrm {Res}}: H^1(S, \Sigma; {\mathbb {R}}^2) \to H^1(S; {\mathbb {R}}^2)$
(given by restricting a cochain to absolute periods). Since
${\mathrm {Res}}: H^1(S, \Sigma; {\mathbb {R}}^2) \to H^1(S; {\mathbb {R}}^2)$
(given by restricting a cochain to absolute periods). Since
![]() ${\mathrm {Res}}$
is topologically defined, its kernel
${\mathrm {Res}}$
is topologically defined, its kernel
![]() $\ker ( {\mathrm {Res}})$
is
$\ker ( {\mathrm {Res}})$
is
![]() $\operatorname {Mod}(S, \Sigma )$
-invariant. Moreover, from our convention that singular points are marked, the
$\operatorname {Mod}(S, \Sigma )$
-invariant. Moreover, from our convention that singular points are marked, the
![]() $\operatorname {Mod}(S, \Sigma )$
-action on
$\operatorname {Mod}(S, \Sigma )$
-action on
![]() $\ker ( {\mathrm {Res}})$
is trivial.
$\ker ( {\mathrm {Res}})$
is trivial.
Let
Since
![]() $H^1(S, \Sigma; {\mathbb {R}}_{\mathrm {x}})$
and
$H^1(S, \Sigma; {\mathbb {R}}_{\mathrm {x}})$
and
![]() $H^1(S, \Sigma; {\mathbb {R}}_{\mathrm {y}})$
are naturally identified with each other via their identification with
$H^1(S, \Sigma; {\mathbb {R}}_{\mathrm {y}})$
are naturally identified with each other via their identification with
![]() $H^1(S, \Sigma; {\mathbb {R}})$
, for each
$H^1(S, \Sigma; {\mathbb {R}})$
, for each
![]() $Z_1 \subset Z$
, we can define the space
$Z_1 \subset Z$
, we can define the space
![]() $\mathfrak {R}_1$
spanned by the two copies of
$\mathfrak {R}_1$
spanned by the two copies of
![]() $Z_1$
in
$Z_1$
in
![]() $H^1(S, \Sigma; {\mathbb {R}}_{\mathrm {x}})$
and
$H^1(S, \Sigma; {\mathbb {R}}_{\mathrm {x}})$
and
![]() $H^1(S, \Sigma; {\mathbb {R}}_{\mathrm {y}})$
, respectively. The space
$H^1(S, \Sigma; {\mathbb {R}}_{\mathrm {y}})$
, respectively. The space
![]() $\mathfrak {R}_1$
is the complexification of
$\mathfrak {R}_1$
is the complexification of
![]() $Z_1$
. This terminology arises from viewing
$Z_1$
. This terminology arises from viewing
![]() $H^1(S, \Sigma; {\mathbb {R}}^2)$
as
$H^1(S, \Sigma; {\mathbb {R}}^2)$
as
![]() $H^1(S, \Sigma; \mathbb {C})$
, a vector space over
$H^1(S, \Sigma; \mathbb {C})$
, a vector space over
![]() $\mathbb {C}$
, and viewing
$\mathbb {C}$
, and viewing
![]() $H^1(S, \Sigma; {\mathbb {R}}_{\mathrm {x}})$
and
$H^1(S, \Sigma; {\mathbb {R}}_{\mathrm {x}})$
and
![]() $H^1(S, \Sigma; {\mathbb {R}}_{\mathrm {y}})$
as the real and imaginary subspace of this complex vector space. With this viewpoint,
$H^1(S, \Sigma; {\mathbb {R}}_{\mathrm {y}})$
as the real and imaginary subspace of this complex vector space. With this viewpoint,
![]() $\mathfrak {R}_1$
is the
$\mathfrak {R}_1$
is the
![]() $\mathbb {C}$
-span of
$\mathbb {C}$
-span of
![]() $Z_1$
.
$Z_1$
.
For any subspace
![]() $Z_1 \subset \mathfrak {R}$
, we can foliate the vector space
$Z_1 \subset \mathfrak {R}$
, we can foliate the vector space
![]() $H^1(S, \Sigma; {\mathbb {R}}^2)$
by affine subspaces parallel to
$H^1(S, \Sigma; {\mathbb {R}}^2)$
by affine subspaces parallel to
![]() $Z_1$
. Pulling back this foliation using the period coordinate charts gives rise to a foliation of
$Z_1$
. Pulling back this foliation using the period coordinate charts gives rise to a foliation of
![]() $\bar {{\mathcal {H}}}_{\mathrm {m}}$
. Since monodromy acts trivially on
$\bar {{\mathcal {H}}}_{\mathrm {m}}$
. Since monodromy acts trivially on
![]() $\mathfrak {R}$
, this foliation descends to a well-defined foliation on
$\mathfrak {R}$
, this foliation descends to a well-defined foliation on
![]() $\bar {\mathcal {H}}$
. It is known (see, for example, [Reference Bainbridge, Smillie and WeissBSW, Prop. 4.1]) that the area of a surface is constant on leaves of the Rel foliation, and thus, the Rel foliation and any of its subfoliations descend to a foliation of
$\bar {\mathcal {H}}$
. It is known (see, for example, [Reference Bainbridge, Smillie and WeissBSW, Prop. 4.1]) that the area of a surface is constant on leaves of the Rel foliation, and thus, the Rel foliation and any of its subfoliations descend to a foliation of
![]() ${\mathcal {H}}$
. The foliation corresponding to
${\mathcal {H}}$
. The foliation corresponding to
![]() $\mathfrak {R}$
(respectively, to Z) is known as the Rel foliation (respectively, the real Rel foliation).
$\mathfrak {R}$
(respectively, to Z) is known as the Rel foliation (respectively, the real Rel foliation).
Because the
![]() $\operatorname {Mod}(S, \Sigma )$
-monodromy action fixes all points of
$\operatorname {Mod}(S, \Sigma )$
-monodromy action fixes all points of
![]() $\mathfrak {R}$
, the leaves of the Rel foliation, and any of its sub-foliations, acquire a translation structure. In particular, they are equipped with a natural measure.
$\mathfrak {R}$
, the leaves of the Rel foliation, and any of its sub-foliations, acquire a translation structure. In particular, they are equipped with a natural measure.
For any
![]() $v \in Z$
, we have a constant vector field, well-defined on
$v \in Z$
, we have a constant vector field, well-defined on
![]() ${{\mathcal {H}}}_{\mathrm {m}}$
and on
${{\mathcal {H}}}_{\mathrm {m}}$
and on
![]() ${{\mathcal {H}}}$
, everywhere equal to v. Integrating this vector field we get a partially defined real REL flow (corresponding to v)
${{\mathcal {H}}}$
, everywhere equal to v. Integrating this vector field we get a partially defined real REL flow (corresponding to v)
![]() ${(t, q) \mapsto \mathrm {Rel}_{tv}(q)}$
; the flow may not be defined for all time due to possible ‘collide of zeroes’. For every
${(t, q) \mapsto \mathrm {Rel}_{tv}(q)}$
; the flow may not be defined for all time due to possible ‘collide of zeroes’. For every
![]() $q \in {{\mathcal {H}}}$
, it is defined for
$q \in {{\mathcal {H}}}$
, it is defined for
![]() $t \in I_q$
, where the domain of definition
$t \in I_q$
, where the domain of definition
![]() $I_q = I_q(v) $
is an open subset of
$I_q = I_q(v) $
is an open subset of
![]() ${\mathbb {R}}$
which contains
${\mathbb {R}}$
which contains
![]() $0$
. The sets
$0$
. The sets
![]() $I_q(v)$
are explicitly described in [Reference Bainbridge, Smillie and WeissBSW, Thm. 6.1]. Let
$I_q(v)$
are explicitly described in [Reference Bainbridge, Smillie and WeissBSW, Thm. 6.1]. Let
![]() $\hat {\mathcal {H}}$
denote the set of surfaces in
$\hat {\mathcal {H}}$
denote the set of surfaces in
![]() ${\mathcal {H}}$
with no horizontal saddle connections. Then
${\mathcal {H}}$
with no horizontal saddle connections. Then
![]() $I_q = {\mathbb {R}}$
for all
$I_q = {\mathbb {R}}$
for all
![]() $q \in \hat {\mathcal {H}}$
.
$q \in \hat {\mathcal {H}}$
.
If
![]() $q \in {{\mathcal {H}}}, \, s \in {\mathbb {R}}$
and
$q \in {{\mathcal {H}}}, \, s \in {\mathbb {R}}$
and
![]() $\tau \in I_q$
, then
$\tau \in I_q$
, then
Similarly, if
![]() $q \in {{\mathcal {H}}}, \, t \in {\mathbb {R}}$
and
$q \in {{\mathcal {H}}}, \, t \in {\mathbb {R}}$
and
![]() $\tau \in I_q$
, then
$\tau \in I_q$
, then
In particular, since P preserves
![]() $\hat {\mathcal {H}}$
and
$\hat {\mathcal {H}}$
and
![]() $P = \{g_t u_s : t, s \in {\mathbb {R}}\}$
, there is an action of
$P = \{g_t u_s : t, s \in {\mathbb {R}}\}$
, there is an action of
![]() $P \ltimes Z$
on
$P \ltimes Z$
on
![]() $\hat {\mathcal {H}}$
, given by
$\hat {\mathcal {H}}$
, given by
![]() $(p, z).q = p \mathrm {Rel}_z(q)$
.
$(p, z).q = p \mathrm {Rel}_z(q)$
.
3. Preliminaries from ergodic theory
3.1. Ergodic decomposition
We will use the notation
![]() $\mathbb {G} \circlearrowright (X, \mu )$
to indicate that
$\mathbb {G} \circlearrowright (X, \mu )$
to indicate that
![]() $\mathbb {G}$
is a locally compact second countable group,
$\mathbb {G}$
is a locally compact second countable group,
![]() $(X, \mathcal {B})$
is a standard Borel space, and
$(X, \mathcal {B})$
is a standard Borel space, and
![]() $\mu $
is a probability measure on
$\mu $
is a probability measure on
![]() $\mathcal {B}$
preserved by the
$\mathcal {B}$
preserved by the
![]() $\mathbb {G}$
-action. We say that
$\mathbb {G}$
-action. We say that
![]() $\mathbb {G} \circlearrowright (Y, \nu )$
is a factor of
$\mathbb {G} \circlearrowright (Y, \nu )$
is a factor of
![]() $(X, \mu )$
if there is a measurable
$(X, \mu )$
if there is a measurable
![]() $\mathbb {G}$
-invariant conull subset
$\mathbb {G}$
-invariant conull subset
![]() $X_0 \subset X$
and a measurable map
$X_0 \subset X$
and a measurable map
![]() $T: X_0 \to Y$
such that
$T: X_0 \to Y$
such that
![]() $T \circ g = g \circ T$
for all
$T \circ g = g \circ T$
for all
![]() $g \in \mathbb {G}$
, and
$g \in \mathbb {G}$
, and
![]() $\nu = T_* \mu $
. In this situation, we refer to T as the factor map. Given a factor map, there is a (unique up to nullsets) measure disintegration
$\nu = T_* \mu $
. In this situation, we refer to T as the factor map. Given a factor map, there is a (unique up to nullsets) measure disintegration
![]() $\mu = \int \mu _y \, d\nu (y)$
, for a Borel mapping
$\mu = \int \mu _y \, d\nu (y)$
, for a Borel mapping
![]() $y \mapsto \mu _y$
from Y to the space of Borel probability measures on X, such that
$y \mapsto \mu _y$
from Y to the space of Borel probability measures on X, such that
![]() $\mu _y(T^{-1}(y))=1$
for
$\mu _y(T^{-1}(y))=1$
for
![]() $\nu $
-a.e. y. Equivalently, we can write
$\nu $
-a.e. y. Equivalently, we can write
![]() $\mu = \int _x \mu ^{\prime }_x \, d\mu (x)$
, where
$\mu = \int _x \mu ^{\prime }_x \, d\mu (x)$
, where
![]() $\mu ^{\prime }_x {\, \stackrel {\mathrm {def}}{=}\, } \mu _{T(x)}$
. For a closed subgroup
$\mu ^{\prime }_x {\, \stackrel {\mathrm {def}}{=}\, } \mu _{T(x)}$
. For a closed subgroup
![]() $H \subset \mathbb {G}$
, we say that
$H \subset \mathbb {G}$
, we say that
![]() $\mu $
is H-ergodic if any invariant set is null or conull. We have the following well-known ergodic decomposition theorem:
$\mu $
is H-ergodic if any invariant set is null or conull. We have the following well-known ergodic decomposition theorem:
Proposition 3.1. Suppose
![]() $\mathbb {G} \circlearrowright (X, \mu )$
, and H is a closed subgroup of
$\mathbb {G} \circlearrowright (X, \mu )$
, and H is a closed subgroup of
![]() $\mathbb {G}$
. Then there is a factor of
$\mathbb {G}$
. Then there is a factor of
![]() $H \circlearrowright (X, \mu )$
, called the space of ergodic components and denoted by
$H \circlearrowright (X, \mu )$
, called the space of ergodic components and denoted by
![]() $X /\!\!/ H$
, with the following properties:
$X /\!\!/ H$
, with the following properties:
-
(i) For
 $\nu $
-a.e.
$\nu $
-a.e.
 $y \in X /\!\!/ H$
,
$y \in X /\!\!/ H$
,
 $\mu _y$
is H-invariant and H-ergodic.
$\mu _y$
is H-invariant and H-ergodic. -
(ii) H acts trivially on
 $X /\!\!/ H$
.
$X /\!\!/ H$
. -
(iii)
 $H \circlearrowright (X, \mu )$
is ergodic if and only if
$H \circlearrowright (X, \mu )$
is ergodic if and only if
 $X /\!\!/ H = \{pt.\}.$
$X /\!\!/ H = \{pt.\}.$
-
(iv) The properties (i)–(iii) uniquely determine the factor
 $X /\!\!/ H$
up to measurable isomorphism.
$X /\!\!/ H$
up to measurable isomorphism. -
(v) If
 $H \lhd \mathbb {G}$
, then
$H \lhd \mathbb {G}$
, then
 $\mathbb {G} \circlearrowright (X /\!\!/ H, \nu )$
.
$\mathbb {G} \circlearrowright (X /\!\!/ H, \nu )$
.
Proof. For (i) and (ii), see [Reference VaradarajanVa, Thm. 4.4] (in the notation of [Reference VaradarajanVa], these assertions follow from the fact that
![]() $\beta $
is a map on points and is H-invariant). Assertion (iii) is immediate from definitions and (iv) follows from [Reference VaradarajanVa, Lemma 4.4]. For (v), one can argue using the uniqueness property (iv), and the fact that the image of an H-invariant ergodic measures under any element
$\beta $
is a map on points and is H-invariant). Assertion (iii) is immediate from definitions and (iv) follows from [Reference VaradarajanVa, Lemma 4.4]. For (v), one can argue using the uniqueness property (iv), and the fact that the image of an H-invariant ergodic measures under any element
![]() $g \in \mathbb {G}$
is also H-invariant and ergodic.
$g \in \mathbb {G}$
is also H-invariant and ergodic.
Remark 3.2. An action is called prime if it has no factors (besides the action itself, and the trivial action on a point). The construction above shows that if
![]() $H \lhd \mathbb {G}$
,
$H \lhd \mathbb {G}$
,
![]() $\mathbb {G}'$
is a subgroup of
$\mathbb {G}'$
is a subgroup of
![]() $\mathbb {G}$
so that
$\mathbb {G}$
so that
![]() $\mathbb {G}' \circlearrowright (X,\mu )$
is prime and
$\mathbb {G}' \circlearrowright (X,\mu )$
is prime and
![]() $H \circlearrowright (X, \mu )$
is not isomorphic to the trivial action, then
$H \circlearrowright (X, \mu )$
is not isomorphic to the trivial action, then
![]() $H \circlearrowright (X, \mu )$
is ergodic. This is not the approach we will take for proving Theorem 1.1.
$H \circlearrowright (X, \mu )$
is ergodic. This is not the approach we will take for proving Theorem 1.1.
3.2. Joinings
We recall some well-known facts about joinings; see [Reference de la RuedlR] and references therein. Let
![]() $\mathbb {G} \circlearrowright (X_i, \mu _i)$
for
$\mathbb {G} \circlearrowright (X_i, \mu _i)$
for
![]() $i=1,2$
. A joining is a measure
$i=1,2$
. A joining is a measure
![]() $ \theta $
on
$ \theta $
on
![]() $X_1 \times X_2$
, invariant under the diagonal action of
$X_1 \times X_2$
, invariant under the diagonal action of
![]() $\mathbb {G}$
, such that
$\mathbb {G}$
, such that
![]() $\pi _{i*} \theta = \mu _i$
. A self-joining is a joining in case
$\pi _{i*} \theta = \mu _i$
. A self-joining is a joining in case
![]() $X_1 = X_2$
. If
$X_1 = X_2$
. If
![]() $(X_i, \mu _i) \to (Z, \nu )$
is a joint factor, then the relatively independent joining over Z is the joining
$(X_i, \mu _i) \to (Z, \nu )$
is a joint factor, then the relatively independent joining over Z is the joining
![]() $\int _Z (\mu _1)_z \times (\mu _2)_z \, d\nu (z)$
, where
$\int _Z (\mu _1)_z \times (\mu _2)_z \, d\nu (z)$
, where
![]() $\mu _i = \int _Z (\mu _i)_z \, d\nu (z)$
is the disintegration of
$\mu _i = \int _Z (\mu _i)_z \, d\nu (z)$
is the disintegration of
![]() $\mu _i$
. In case
$\mu _i$
. In case
![]() $X_1 = X_2 =X$
, and
$X_1 = X_2 =X$
, and
![]() $Z = X /\!\!/ H$
is the space of ergodic components of the action of H on
$Z = X /\!\!/ H$
is the space of ergodic components of the action of H on
![]() $(X, \mu )$
as in Proposition 3.1, we obtain the relatively independent self-joining over
$(X, \mu )$
as in Proposition 3.1, we obtain the relatively independent self-joining over
![]() $X /\!\!/ H$
. From the definitions, one finds that this joining satisfies:
$X /\!\!/ H$
. From the definitions, one finds that this joining satisfies:
Proposition 3.3. The following are equivalent:
-
•
 $H \circlearrowright (X, \mu )$
is ergodic.
$H \circlearrowright (X, \mu )$
is ergodic. -
•
 $X /\!\!/ H = \{pt.\}$
.
$X /\!\!/ H = \{pt.\}$
. -
• The relatively independent self-joining over
 $X /\!\!/ H$
is
$X /\!\!/ H$
is
 $\mu \times \mu $
.
$\mu \times \mu $
.
We note three properties of this self-joining. We fix a topology on X which generates the
![]() $\sigma $
-algebra and denote by
$\sigma $
-algebra and denote by
![]() $\mathrm {supp} \, \mu $
the topological support of
$\mathrm {supp} \, \mu $
the topological support of
![]() $\mu $
(i.e., the smallest closed set of full measure).
$\mu $
(i.e., the smallest closed set of full measure).
Proposition 3.4. Let
![]() $\theta $
be the measure on
$\theta $
be the measure on
![]() $X \times X$
which is the relatively independent self-joining over
$X \times X$
which is the relatively independent self-joining over
![]() $X /\!\!/ H$
, for some H, and let
$X /\!\!/ H$
, for some H, and let
![]() $T: X \to X /\!\!/ H$
be the factor map. Then the following hold:
$T: X \to X /\!\!/ H$
be the factor map. Then the following hold:
-
• We have
(3.1) $$ \begin{align} \theta = \int_X \mu_{T(x)} \times \mu_{T(x)} \, d\mu(x). \end{align} $$
$$ \begin{align} \theta = \int_X \mu_{T(x)} \times \mu_{T(x)} \, d\mu(x). \end{align} $$
-
• The set
 $\left \{x \in X : x \notin \mathrm {supp} \, \mu _{T(x)} \right \}$
is of
$\left \{x \in X : x \notin \mathrm {supp} \, \mu _{T(x)} \right \}$
is of
 $\mu $
-measure zero.
$\mu $
-measure zero. -
• If
 $X = \mathrm {supp} \, \mu $
, then
$X = \mathrm {supp} \, \mu $
, then
 $\mathrm {supp} \, \theta $
contains the diagonal
$\mathrm {supp} \, \theta $
contains the diagonal
 $\Delta _X {\, \stackrel {\mathrm {def}}{=}\, } \{(x,x) : x \in X\}$
.
$\Delta _X {\, \stackrel {\mathrm {def}}{=}\, } \{(x,x) : x \in X\}$
.
Proof. Formula (3.1) is immediate from the definition of the relatively independent self-joining over
![]() $X /\!\!/ H$
. Since each
$X /\!\!/ H$
. Since each
![]() $\mu ^{\prime }_x = \mu _{T(x)}$
is H-invariant and ergodic, and
$\mu ^{\prime }_x = \mu _{T(x)}$
is H-invariant and ergodic, and
![]() $\mu ^{\prime }_x(T^{-1}(T(x)))=1$
, the set
$\mu ^{\prime }_x(T^{-1}(T(x)))=1$
, the set
![]() $\{x \in X: x \notin \mathrm {supp} \, \mu ^{\prime }_x\}$
is a
$\{x \in X: x \notin \mathrm {supp} \, \mu ^{\prime }_x\}$
is a
![]() $\mu $
-nullset. For the last assertion, given
$\mu $
-nullset. For the last assertion, given
![]() $(x_0, x_0) \in X \times X$
, and a neighborhood
$(x_0, x_0) \in X \times X$
, and a neighborhood
![]() $\mathcal {U}$
of
$\mathcal {U}$
of
![]() $(x_0,x_0)$
, we need to show that
$(x_0,x_0)$
, we need to show that
![]() $\theta (\mathcal {U})>0$
. We can assume with no loss of generality that
$\theta (\mathcal {U})>0$
. We can assume with no loss of generality that
![]() $\mathcal {U} = \mathcal {O} \times \mathcal {O}$
for an open set
$\mathcal {U} = \mathcal {O} \times \mathcal {O}$
for an open set
![]() $\mathcal {O} \subset X$
containing
$\mathcal {O} \subset X$
containing
![]() $x_0$
. Since
$x_0$
. Since
![]() $\mathrm {supp} \, \mu = X$
, we have
$\mathrm {supp} \, \mu = X$
, we have
![]() $\mu (\mathcal {O})>0$
, and by the preceding discussion, for a.e.
$\mu (\mathcal {O})>0$
, and by the preceding discussion, for a.e.
![]() $x \in \mathcal {O}$
,
$x \in \mathcal {O}$
,
![]() $x \in \mathrm {supp} \, \mu ^{\prime }_x$
, and hence,
$x \in \mathrm {supp} \, \mu ^{\prime }_x$
, and hence,
![]() $\mu ^{\prime }_x(\mathcal {O})>0$
. Now the result follows from (3.1).
$\mu ^{\prime }_x(\mathcal {O})>0$
. Now the result follows from (3.1).
Example 3.5 (Branched covers, cont.).
With the notation of Example 1.3, the relatively independent self-joining
![]() $\theta $
can be written as
$\theta $
can be written as
where
![]() $\nu _q$
is the natural translation invariant measure on the leaf
$\nu _q$
is the natural translation invariant measure on the leaf
![]() $\mathfrak {R}_1(q)$
, which is identified with the underlying surface
$\mathfrak {R}_1(q)$
, which is identified with the underlying surface
![]() $M_q$
, and which we embed in
$M_q$
, and which we embed in
![]() ${{\mathcal L}} \times {{\mathcal L}}$
via the map
${{\mathcal L}} \times {{\mathcal L}}$
via the map
3.3. Ergodicity, mixing, and mixing of all orders
For
![]() $\mathbb {G} \circlearrowright (X, \mu )$
, let
$\mathbb {G} \circlearrowright (X, \mu )$
, let
![]() $L^2_0(\mu )$
denote the Hilbert space of
$L^2_0(\mu )$
denote the Hilbert space of
![]() $L^2$
-functions on
$L^2$
-functions on
![]() $(X, \mu )$
of integral zero, and let
$(X, \mu )$
of integral zero, and let
![]() $k \geq 2$
. The action is called k-mixing if for any
$k \geq 2$
. The action is called k-mixing if for any
![]() $f_1, \ldots , f_k \in L^2_0(\mu )$
and for any
$f_1, \ldots , f_k \in L^2_0(\mu )$
and for any
![]() $k-1$
sequences
$k-1$
sequences
![]() $\left (g^{(i)}_n \right )_{n \in {\mathbb {N}}} \in \mathbb {G}, \ i=1, \ldots , k-1$
, for which all of the sequences
$\left (g^{(i)}_n \right )_{n \in {\mathbb {N}}} \in \mathbb {G}, \ i=1, \ldots , k-1$
, for which all of the sequences
eventually leave every compact subset of
![]() $\mathbb {G}$
, we have
$\mathbb {G}$
, we have
 $$ \begin{align*}\int_X f_1\left(g^{(1)}_nx \right) \cdots f_{k-1}\left(g_n^{(k-1)}x \right) f_k(x) \, d\mu(x) \stackrel{n \to \infty}{\longrightarrow} \prod_{i=1}^k \int_X f_i \, d\mu=0. \end{align*} $$
$$ \begin{align*}\int_X f_1\left(g^{(1)}_nx \right) \cdots f_{k-1}\left(g_n^{(k-1)}x \right) f_k(x) \, d\mu(x) \stackrel{n \to \infty}{\longrightarrow} \prod_{i=1}^k \int_X f_i \, d\mu=0. \end{align*} $$
We say that the action is mixing if it is 2-mixing, and mixing of all orders if it is mixing of order k for any
![]() $k \geq 2$
. It is easy to check that mixing implies ergodicity of any unbounded subgroup of
$k \geq 2$
. It is easy to check that mixing implies ergodicity of any unbounded subgroup of
![]() $\mathbb {G}$
. We have the following:
$\mathbb {G}$
. We have the following:
Proposition 3.6. Let
![]() $Z_0 \cong {\mathbb {R}}$
, and let
$Z_0 \cong {\mathbb {R}}$
, and let
![]() $\{g_t\}$
be a one-parameter group acting on
$\{g_t\}$
be a one-parameter group acting on
![]() $Z_0$
by dilations (i.e., for all
$Z_0$
by dilations (i.e., for all
![]() $v \in Z_0$
and
$v \in Z_0$
and
![]() $t \in {\mathbb {R}}$
we have
$t \in {\mathbb {R}}$
we have
![]() $g_t v = e^{\lambda t}v$
for some
$g_t v = e^{\lambda t}v$
for some
![]() $\lambda \neq 0$
). Let
$\lambda \neq 0$
). Let
![]() $F = \{g_t \} \ltimes Z_0$
, and let
$F = \{g_t \} \ltimes Z_0$
, and let
![]() $F \circlearrowright (X, \mu )$
be a probability space. The following are equivalent:
$F \circlearrowright (X, \mu )$
be a probability space. The following are equivalent:
-
(a) the restricted flow
 $Z_0\circlearrowright (X, \mu )$
is ergodic;
$Z_0\circlearrowright (X, \mu )$
is ergodic; -
(b) the restricted flow
 $Z_0\circlearrowright (X, \mu )$
is mixing of all orders;
$Z_0\circlearrowright (X, \mu )$
is mixing of all orders; -
(c) the restricted flow
 $Z_0\circlearrowright (X, \mu )$
is mixing;
$Z_0\circlearrowright (X, \mu )$
is mixing; -
(d) any nontrivial element of
 $Z_0$
acts ergodically.
$Z_0$
acts ergodically.
Remark 3.7. The group F appearing in Proposition 3.6 is isomorphic as a Lie group to the subgroup P of upper triangular matrices in G, but in our application, we will use it for the group generated by a one-parameter real Rel flow
![]() $Z_0$
and the diagonal flow
$Z_0$
and the diagonal flow
![]() $\{g_t\}$
.
$\{g_t\}$
.
Proof. Clearly, (b)
![]() $\implies $
(c)
$\implies $
(c)
![]() $\implies $
(d)
$\implies $
(d)
![]() $\implies $
(a). We assume that the
$\implies $
(a). We assume that the
![]() $Z_0$
-flow is ergodic. To see that it is mixing, it is enough by [Reference PetersenP, Chap. 2, Prop. 5.9] to prove that it has countable Lebesgue spectrum, and for this, use [Reference Katok and ThouvenotKT, Prop. 1.23 & Prop. 2.2]. The proof of mixing of all orders follows verbatim from an argument of Mozes [Reference MozesMo] for mixing actions of Lie groups which are ‘Ad-proper’. Since our group
$Z_0$
-flow is ergodic. To see that it is mixing, it is enough by [Reference PetersenP, Chap. 2, Prop. 5.9] to prove that it has countable Lebesgue spectrum, and for this, use [Reference Katok and ThouvenotKT, Prop. 1.23 & Prop. 2.2]. The proof of mixing of all orders follows verbatim from an argument of Mozes [Reference MozesMo] for mixing actions of Lie groups which are ‘Ad-proper’. Since our group
![]() $ F$
is not Ad-proper, we cannot cite [Reference MozesMo] directly, so we sketch the proof. For notational convenience, we deduce 3-fold mixing from mixing (the proof that ‘k-fold mixing
$ F$
is not Ad-proper, we cannot cite [Reference MozesMo] directly, so we sketch the proof. For notational convenience, we deduce 3-fold mixing from mixing (the proof that ‘k-fold mixing
![]() $\implies k+1$
-fold mixing’, for
$\implies k+1$
-fold mixing’, for
![]() $k \geq 3$
, is identical but requires more cumbersome notation).
$k \geq 3$
, is identical but requires more cumbersome notation).
We use additive notation in the group
![]() $Z_0$
and denote the action of
$Z_0$
and denote the action of
![]() $Z_0$
on X by
$Z_0$
on X by
![]() $(z,x) \mapsto z.x$
. Let
$(z,x) \mapsto z.x$
. Let
![]() $\left (b_n\right )_{n \in {\mathbb {N}}}$
and
$\left (b_n\right )_{n \in {\mathbb {N}}}$
and
![]() $\left (c_n \right )_{n \in {\mathbb {N}}}$
be sequences in
$\left (c_n \right )_{n \in {\mathbb {N}}}$
be sequences in
![]() $Z_0$
such that each of the sequences
$Z_0$
such that each of the sequences
![]() $\left (b_n\right )_{n \in {\mathbb {N}}}, \, \left (c_n\right )_{n \in {\mathbb {N}}}, \, \left (b_n+ c_n\right )_{n \in {\mathbb {N}}} $
eventually leaves every compact set, and let
$\left (b_n\right )_{n \in {\mathbb {N}}}, \, \left (c_n\right )_{n \in {\mathbb {N}}}, \, \left (b_n+ c_n\right )_{n \in {\mathbb {N}}} $
eventually leaves every compact set, and let
![]() $f_1, f_2, f_3$
be in
$f_1, f_2, f_3$
be in
![]() $L^2_0(\mu )$
. We need to prove that
$L^2_0(\mu )$
. We need to prove that
For each n, define a measure
![]() $\mu _n$
on
$\mu _n$
on
![]() $X^3 {\, \stackrel {\mathrm {def}}{=}\, } X \times X \times X$
by
$X^3 {\, \stackrel {\mathrm {def}}{=}\, } X \times X \times X$
by
That is,
![]() $\mu _n$
is the pushforward of the diagonal measure on
$\mu _n$
is the pushforward of the diagonal measure on
![]() $X^3$
by the triple
$X^3$
by the triple
![]() $(0, b_n, b_n+c_n)$
. It is easy to see that 3-mixing is equivalent to the fact that the weak-* limit of
$(0, b_n, b_n+c_n)$
. It is easy to see that 3-mixing is equivalent to the fact that the weak-* limit of
![]() $\mu _n$
is the measure
$\mu _n$
is the measure
![]() $\mu ^3 {\, \stackrel {\mathrm {def}}{=}\, } \mu \times \mu \times \mu $
. The group
$\mu ^3 {\, \stackrel {\mathrm {def}}{=}\, } \mu \times \mu \times \mu $
. The group
![]() $F^3 {\, \stackrel {\mathrm {def}}{=}\, } F\times F \times F$
acts on
$F^3 {\, \stackrel {\mathrm {def}}{=}\, } F\times F \times F$
acts on
![]() $X^3$
by acting separately on each component, and as in [Reference MozesMo], since
$X^3$
by acting separately on each component, and as in [Reference MozesMo], since
![]() $Z_0$
is mixing, it suffices to show that any measure
$Z_0$
is mixing, it suffices to show that any measure
![]() $\nu $
on
$\nu $
on
![]() $X^3$
which is a weak-* limit of a subsequence of
$X^3$
which is a weak-* limit of a subsequence of
![]() $\left (\mu _n\right )_{n \in {\mathbb {N}}}$
, is invariant under
$\left (\mu _n\right )_{n \in {\mathbb {N}}}$
, is invariant under
![]() $(0, u, v) \in {\mathbb {R}}^{3} \subset F^3,$
for some
$(0, u, v) \in {\mathbb {R}}^{3} \subset F^3,$
for some
![]() $(u,v) \in {\mathbb {R}}^{2} \smallsetminus (0,0)$
. We claim that for any
$(u,v) \in {\mathbb {R}}^{2} \smallsetminus (0,0)$
. We claim that for any
![]() $s \in {\mathbb {R}}$
, the measure
$s \in {\mathbb {R}}$
, the measure
![]() $\mu _n$
is invariant under
$\mu _n$
is invariant under
where the multiplication is in the group
![]() $F^3$
. Indeed, since
$F^3$
. Indeed, since
![]() $\mu $
is
$\mu $
is
![]() $\{g_s\}$
-invariant,
$\{g_s\}$
-invariant,
and
That is, applying
![]() $h_n (s) $
changes one description of
$h_n (s) $
changes one description of
![]() $\mu _n$
to another.
$\mu _n$
to another.
We embed F as a multiplicative group of matrices in
![]() $\operatorname {GL}_{2}({\mathbb {R}})$
and let
$\operatorname {GL}_{2}({\mathbb {R}})$
and let
![]() $d_F$
be the metric on F induced by some norm on
$d_F$
be the metric on F induced by some norm on
![]() $\operatorname {GL}_{2}({\mathbb {R}}) $
. By a straightforward computation, we have
$\operatorname {GL}_{2}({\mathbb {R}}) $
. By a straightforward computation, we have
and
![]() $d_F(\mathrm {id}_F, h_n(s))$
is a continuous function of s which goes to
$d_F(\mathrm {id}_F, h_n(s))$
is a continuous function of s which goes to
![]() $0$
as
$0$
as
![]() $s \to 0$
and for any fixed
$s \to 0$
and for any fixed
![]() $s>0$
, increases to infinity as
$s>0$
, increases to infinity as
![]() $n \to \infty $
. Therefore, we can choose
$n \to \infty $
. Therefore, we can choose
![]() $s_n \to 0$
so that
$s_n \to 0$
so that
![]() $d_F(\mathrm {id}_F, h_n(s_n))=1$
for all large enough n. As in [Reference MozesMo],
$d_F(\mathrm {id}_F, h_n(s_n))=1$
for all large enough n. As in [Reference MozesMo],
![]() $\nu $
is invariant under some subsequential limit of
$\nu $
is invariant under some subsequential limit of
![]() $h_n(s_n)$
which is of the form
$h_n(s_n)$
which is of the form
![]() $(0, u, v)$
for some
$(0, u, v)$
for some
![]() $(u, v) \in {\mathbb {R}}^{2} \smallsetminus (0,0)$
. This establishes our sufficient condition.
$(u, v) \in {\mathbb {R}}^{2} \smallsetminus (0,0)$
. This establishes our sufficient condition.
4. The relatively independent self-joining for a Rel flow
Recall that
![]() $\hat {{\mathcal L}} \subset {{\mathcal L}}$
is the set of surfaces without horizontal saddle connections, and this is a P-invariant set of full measure with respect to
$\hat {{\mathcal L}} \subset {{\mathcal L}}$
is the set of surfaces without horizontal saddle connections, and this is a P-invariant set of full measure with respect to
![]() $m_{{{\mathcal L}}}$
. We can combine the product action of
$m_{{{\mathcal L}}}$
. We can combine the product action of
![]() $Z_{{\mathcal L}} \times Z_{{\mathcal L}}$
on
$Z_{{\mathcal L}} \times Z_{{\mathcal L}}$
on
![]() $\hat {{\mathcal L}} \times \hat {{\mathcal L}}$
with the diagonal action of P to obtain an action of the semi-direct product
$\hat {{\mathcal L}} \times \hat {{\mathcal L}}$
with the diagonal action of P to obtain an action of the semi-direct product
![]() $P \ltimes (Z_{{\mathcal L}} \times Z_{{\mathcal L}})$
on
$P \ltimes (Z_{{\mathcal L}} \times Z_{{\mathcal L}})$
on
![]() $\hat {{\mathcal L}} \times \hat {{\mathcal L}}$
. Since
$\hat {{\mathcal L}} \times \hat {{\mathcal L}}$
. Since
![]() $\hat {{\mathcal L}} \subset {{\mathcal L}}$
is of full measure, and the arguments of this section involve passing to sets of full measure, in the remainder of this section, we will ignore the distinction between
$\hat {{\mathcal L}} \subset {{\mathcal L}}$
is of full measure, and the arguments of this section involve passing to sets of full measure, in the remainder of this section, we will ignore the distinction between
![]() ${{\mathcal L}}$
and
${{\mathcal L}}$
and
![]() $\hat {{\mathcal L}}$
.
$\hat {{\mathcal L}}$
.
Proposition 4.1. Let
![]() $Z \subset Z_{{\mathcal L}}$
be a closed connected subgroup. If
$Z \subset Z_{{\mathcal L}}$
be a closed connected subgroup. If
![]() $\theta $
is an invariant probability measure for an action of the semidirect product
$\theta $
is an invariant probability measure for an action of the semidirect product
![]() $P \ltimes (Z\times Z)$
on
$P \ltimes (Z\times Z)$
on
![]() ${{\mathcal L}} \times {{\mathcal L}}$
, then any
${{\mathcal L}} \times {{\mathcal L}}$
, then any
![]() $f \in L^2(\theta )$
which is
$f \in L^2(\theta )$
which is
![]() $\{g_t\}$
-invariant is also
$\{g_t\}$
-invariant is also
![]() $Z \times Z$
-invariant.
$Z \times Z$
-invariant.
Proof. For any
![]() $z \in Z \times Z$
,
$z \in Z \times Z$
,
![]() $g_t z g_{-t} \to _{t \to -\infty } 0$
. So the claim follows from the Mautner phenomenon; see, for example, [Reference Einsiedler and WardEW, Prop 11.18].
$g_t z g_{-t} \to _{t \to -\infty } 0$
. So the claim follows from the Mautner phenomenon; see, for example, [Reference Einsiedler and WardEW, Prop 11.18].
Proposition 4.2. Let
![]() $({{\mathcal L}}, m_{{\mathcal L}})$
be a G-orbit-closure with a fully supported
$({{\mathcal L}}, m_{{\mathcal L}})$
be a G-orbit-closure with a fully supported
![]() $ P$
-invariant ergodic measure, let
$ P$
-invariant ergodic measure, let
![]() $Z \subset Z_{{\mathcal L}}$
be a connected closed subgroup, and let
$Z \subset Z_{{\mathcal L}}$
be a connected closed subgroup, and let
![]() $\theta $
on
$\theta $
on
![]() ${{\mathcal L}}\times {{\mathcal L}}$
be the relatively independent joining over
${{\mathcal L}}\times {{\mathcal L}}$
be the relatively independent joining over
![]() ${{\mathcal L}} /\!\!/ Z$
. Then
${{\mathcal L}} /\!\!/ Z$
. Then
![]() $\theta $
is P-invariant and
$\theta $
is P-invariant and
![]() $\{g_t\}$
-ergodic (and hence P-ergodic). Also
$\{g_t\}$
-ergodic (and hence P-ergodic). Also
![]() $\Delta _{{{\mathcal L}}} \subset \mathrm {supp} \, \theta $
.
$\Delta _{{{\mathcal L}}} \subset \mathrm {supp} \, \theta $
.
As we will see in §5, under the conditions of the Proposition,
![]() $m_{{\mathcal L}}$
is the so-called ‘flat measure’ on
$m_{{\mathcal L}}$
is the so-called ‘flat measure’ on
![]() ${{\mathcal L}}$
.
${{\mathcal L}}$
.
Proof. Let
![]() $\pi : {\mathcal L} \times {\mathcal L} \to {{\mathcal L}}$
be the projection onto the first factor, and let
$\pi : {\mathcal L} \times {\mathcal L} \to {{\mathcal L}}$
be the projection onto the first factor, and let
![]() $\nu = \pi _* \theta .$
We have
$\nu = \pi _* \theta .$
We have
![]() $\nu = m_{{{\mathcal L}}}$
by (3.1) and the properties of the ergodic decomposition. For each
$\nu = m_{{{\mathcal L}}}$
by (3.1) and the properties of the ergodic decomposition. For each
![]() $x \in {{\mathcal L}}$
, let
$x \in {{\mathcal L}}$
, let
![]() $\Omega _x {\, \stackrel {\mathrm {def}}{=}\, } \pi ^{-1}(x) = \{x\} \times {{\mathcal L}}$
be the fiber, and let
$\Omega _x {\, \stackrel {\mathrm {def}}{=}\, } \pi ^{-1}(x) = \{x\} \times {{\mathcal L}}$
be the fiber, and let
![]() $\theta _x$
be the fiber measure appearing in the disintegration
$\theta _x$
be the fiber measure appearing in the disintegration
![]() $\theta = \int _{{{\mathcal L}} } \theta _x \, d\nu (x)$
. Then Z acts on
$\theta = \int _{{{\mathcal L}} } \theta _x \, d\nu (x)$
. Then Z acts on
![]() $\Omega _x$
via the second factor in
$\Omega _x$
via the second factor in
![]() $Z \times Z$
, and
$Z \times Z$
, and
![]() $\theta _x$
is Z-invariant and ergodic by the definition of the ergodic decomposition and Proposition 3.1(i) (with
$\theta _x$
is Z-invariant and ergodic by the definition of the ergodic decomposition and Proposition 3.1(i) (with
![]() $H=Z$
).
$H=Z$
).
It follows from Proposition 3.1(v) (with
![]() $\mathbb {G} = P \ltimes (Z \times Z)$
) that
$\mathbb {G} = P \ltimes (Z \times Z)$
) that
![]() $\theta $
is P-invariant. To prove ergodicity, let
$\theta $
is P-invariant. To prove ergodicity, let
![]() $f \in L^2({{\mathcal L}} \times {{\mathcal L}}, \theta )$
be a P-invariant function. By Proposition 4.1, f is
$f \in L^2({{\mathcal L}} \times {{\mathcal L}}, \theta )$
be a P-invariant function. By Proposition 4.1, f is
![]() $Z \times Z$
-invariant. For each
$Z \times Z$
-invariant. For each
![]() $x \in {{\mathcal L}}$
, let
$x \in {{\mathcal L}}$
, let
![]() $f_x {\, \stackrel {\mathrm {def}}{=}\, } f|_{\Omega _x}$
. There is
$f_x {\, \stackrel {\mathrm {def}}{=}\, } f|_{\Omega _x}$
. There is
![]() ${{\mathcal L}}_0 \subset {{\mathcal L}}$
such that
${{\mathcal L}}_0 \subset {{\mathcal L}}$
such that
![]() $m_{{{\mathcal L}}}({{\mathcal L}}_0)=1$
, and for every
$m_{{{\mathcal L}}}({{\mathcal L}}_0)=1$
, and for every
![]() $x \in {{\mathcal L}}_0$
,
$x \in {{\mathcal L}}_0$
,
![]() $f_x $
belongs to
$f_x $
belongs to
![]() $ L^2(\Omega _x, \theta _x)$
and is Z-invariant. Hence, by ergodicity, there is
$ L^2(\Omega _x, \theta _x)$
and is Z-invariant. Hence, by ergodicity, there is
![]() $\bar {f}: {{\mathcal L}}_0 \to {\mathbb {R}}$
such that for every
$\bar {f}: {{\mathcal L}}_0 \to {\mathbb {R}}$
such that for every
![]() $ x\in {{\mathcal L}}_0$
,
$ x\in {{\mathcal L}}_0$
,
![]() $\bar {f}(x)$
is the
$\bar {f}(x)$
is the
![]() $\theta _x$
-almost-sure value of
$\theta _x$
-almost-sure value of
![]() $f_x$
. Since f is P-invariant for the diagonal action of P,
$f_x$
. Since f is P-invariant for the diagonal action of P,
![]() $\bar {f}$
is P-invariant for the action of P on
$\bar {f}$
is P-invariant for the action of P on
![]() ${{\mathcal L}}$
. By ergodicity of
${{\mathcal L}}$
. By ergodicity of
![]() $P \circlearrowright ({{\mathcal L}}, m_{{\mathcal L}})$
,
$P \circlearrowright ({{\mathcal L}}, m_{{\mathcal L}})$
,
![]() $\bar f$
is
$\bar f$
is
![]() $\nu $
-a.e. constant, and thus, f is
$\nu $
-a.e. constant, and thus, f is
![]() $\theta $
-a.e. constant.
$\theta $
-a.e. constant.
The last assertion follows from Proposition 3.4.
5. An upgraded magic wand theorem
The celebrated ‘magic wand’ Theorem of Eskin and Mirzakhani [Reference Eskin and MirzakhaniEM], and ensuing work of Eskin, Mirzakhani and Mohammadi [Reference Eskin, Mirzakhani and MohammadiEMM], classified P- and G-invariant probability measures and orbit-closures on strata of translation surfaces. These results can be summarized as follows (see [Reference Eskin and MirzakhaniEM, Defs. 1.1 & 1.2, Thms. 1.4 & 1.5]):
Theorem 5.1. Let
![]() ${\mathcal {H}}, \, {\mathcal {H}}_{\mathrm {m}}, \, \bar {{\mathcal {H}}}, \, \bar {{\mathcal {H}}}_{\mathrm {m}}$
be as in §2.1. Any P-invariant ergodic probability measure m has the following properties:
${\mathcal {H}}, \, {\mathcal {H}}_{\mathrm {m}}, \, \bar {{\mathcal {H}}}, \, \bar {{\mathcal {H}}}_{\mathrm {m}}$
be as in §2.1. Any P-invariant ergodic probability measure m has the following properties:
-
(i) It is G-invariant.
-
(ii) There is a complex-affine manifold
 $\mathcal {N}$
and a proper immersion
$\mathcal {N}$
and a proper immersion
 $\varphi : \mathcal {N} \to \bar {{\mathcal {H}}}$
such that
$\varphi : \mathcal {N} \to \bar {{\mathcal {H}}}$
such that  $$ \begin{align*}{{\mathcal L}} {\, \stackrel{\mathrm{def}}{=}\, } \mathrm{supp} \, m = {{\mathcal{H}}} \cap \varphi(\mathcal{N}).\end{align*} $$
$$ \begin{align*}{{\mathcal L}} {\, \stackrel{\mathrm{def}}{=}\, } \mathrm{supp} \, m = {{\mathcal{H}}} \cap \varphi(\mathcal{N}).\end{align*} $$
-
(iii) There is an open G-invariant subset
 $U \subset \bar {{\mathcal {H}}}$
satisfying
$U \subset \bar {{\mathcal {H}}}$
satisfying
 $m(U )=1$
, and for any
$m(U )=1$
, and for any
 $x \in U \cap {{\mathcal L}}$
, there is an open set V containing x such that V is evenly covered by
$x \in U \cap {{\mathcal L}}$
, there is an open set V containing x such that V is evenly covered by
 $\mathcal {V} \subset {{\mathcal {H}}}_{\mathrm {m}}$
under the map
$\mathcal {V} \subset {{\mathcal {H}}}_{\mathrm {m}}$
under the map
 $\pi : \bar {{{\mathcal {H}}}}_{\mathrm {m}} \to \bar {{{\mathcal {H}}}}$
, and
$\pi : \bar {{{\mathcal {H}}}}_{\mathrm {m}} \to \bar {{{\mathcal {H}}}}$
, and
 $\psi {\, \stackrel {\mathrm {def}}{=}\, } \mathrm {dev} \circ (\pi |_{\mathcal {V}})^{-1} \circ \varphi $
coincides on its domain with a
$\psi {\, \stackrel {\mathrm {def}}{=}\, } \mathrm {dev} \circ (\pi |_{\mathcal {V}})^{-1} \circ \varphi $
coincides on its domain with a
 $\mathbb {C}$
-linear map, with real coefficients.
$\mathbb {C}$
-linear map, with real coefficients. -
(iv) The subspace
 $W{\, \stackrel {\mathrm {def}}{=}\, } \mathrm {Im} (\psi )$
satisfies that
$W{\, \stackrel {\mathrm {def}}{=}\, } \mathrm {Im} (\psi )$
satisfies that
 $\mathrm {Res}(W)$
symplectic, and the measure m is obtained via the cone construction from the Lebesgue measures on
$\mathrm {Res}(W)$
symplectic, and the measure m is obtained via the cone construction from the Lebesgue measures on
 $\mathrm {Res}(W)$
and on
$\mathrm {Res}(W)$
and on
 $\mathfrak {R} \cap W$
.
$\mathfrak {R} \cap W$
. -
(v) The complement
 ${{\mathcal L}} \smallsetminus U$
is a finite union of supports of measures satisfying properties (i)–(iv), for which the manifolds
${{\mathcal L}} \smallsetminus U$
is a finite union of supports of measures satisfying properties (i)–(iv), for which the manifolds
 $\mathcal {N}'$
appearing in (ii) satisfy
$\mathcal {N}'$
appearing in (ii) satisfy
 $\dim \mathcal {N}' < \dim \mathcal {N}.$
$\dim \mathcal {N}' < \dim \mathcal {N}.$
Any orbit-closure for the P-action is a set
![]() ${{\mathcal L}}$
as above.
${{\mathcal L}}$
as above.
The description of
![]() $m_{{{\mathcal L}}}$
in item (iv) means that we fix a normalization
$m_{{{\mathcal L}}}$
in item (iv) means that we fix a normalization
![]() $\mathrm {Leb}_W$
of Lebesgue measure on W using the symplectic structure on
$\mathrm {Leb}_W$
of Lebesgue measure on W using the symplectic structure on
![]() $\mathrm {Res}(W)$
and the translation structure on
$\mathrm {Res}(W)$
and the translation structure on
![]() $\mathfrak {R} \cap W$
, and for a Borel subset
$\mathfrak {R} \cap W$
, and for a Borel subset
![]() $A \subset V \subset {{\mathcal L}}$
, where
$A \subset V \subset {{\mathcal L}}$
, where
![]() $V = \pi (\mathcal {V})$
is as in item (iii), we have
$V = \pi (\mathcal {V})$
is as in item (iii), we have
We will refer to
![]() ${{\mathcal L}}$
as an orbit-closure and to
${{\mathcal L}}$
as an orbit-closure and to
![]() $m = m_{{\mathcal L}}$
as a flat measure on
$m = m_{{\mathcal L}}$
as a flat measure on
![]() ${{\mathcal L}}$
. Orbit-closures are referred to as affine invariant manifolds and also as invariant subvarieties. The use of an evenly covered neighborhood in item (iii) is a standard approach for defining period coordinates (see, for example, [Reference Masur and SmillieMS]).
${{\mathcal L}}$
. Orbit-closures are referred to as affine invariant manifolds and also as invariant subvarieties. The use of an evenly covered neighborhood in item (iii) is a standard approach for defining period coordinates (see, for example, [Reference Masur and SmillieMS]).
It is easy to check, using our convention that singularities are labeled, that
![]() $\mathfrak {R}_{{{\mathcal L}}} {\, \stackrel {\mathrm {def}}{=}\, } \mathfrak {R} \cap \mathrm {Im }(\psi )$
is well defined; that is, it does not depend on the choice of the neighborhood
$\mathfrak {R}_{{{\mathcal L}}} {\, \stackrel {\mathrm {def}}{=}\, } \mathfrak {R} \cap \mathrm {Im }(\psi )$
is well defined; that is, it does not depend on the choice of the neighborhood
![]() $\mathcal {V}$
used in (iii) (see, for example, [Reference Chaika, Weiss and YgoufCWY, §2.3]). The statement in item (iv) that
$\mathcal {V}$
used in (iii) (see, for example, [Reference Chaika, Weiss and YgoufCWY, §2.3]). The statement in item (iv) that
![]() $\mathrm {Res}(W)$
is symplectic is proved in [Reference Artur, Alex and MöllerAEM]. We refer to [Reference WrightWr1] for a survey containing more information on orbit-closures.
$\mathrm {Res}(W)$
is symplectic is proved in [Reference Artur, Alex and MöllerAEM]. We refer to [Reference WrightWr1] for a survey containing more information on orbit-closures.
In a forthcoming work of Brown, Eskin, Filip and Rodriguez-Hertz, the same conclusion is obtained for the diagonal actions of P and G on a product of strata
![]() ${{\mathcal {H}}} \times {{\mathcal {H}}}'$
. Namely, the following is shown:
${{\mathcal {H}}} \times {{\mathcal {H}}}'$
. Namely, the following is shown:
Statement A. Let
![]() ${{\mathcal {H}}}, {{\mathcal {H}}}'$
be strata of translation surfaces, and let Pand Gact on
${{\mathcal {H}}}, {{\mathcal {H}}}'$
be strata of translation surfaces, and let Pand Gact on
![]() ${{\mathcal {H}}} \times {{\mathcal {H}}}'$
via their diagonal embeddings in
${{\mathcal {H}}} \times {{\mathcal {H}}}'$
via their diagonal embeddings in
![]() $G \times G$
. Then all of the conclusions of Theorem 5.1 hold for this action (with
$G \times G$
. Then all of the conclusions of Theorem 5.1 hold for this action (with
![]() ${\bar {\mathcal {H}}\times \bar {\mathcal {H}}'}$
replacing
${\bar {\mathcal {H}}\times \bar {\mathcal {H}}'}$
replacing
![]() $\bar {\mathcal {H}}$
).
$\bar {\mathcal {H}}$
).
We refer to this as a ‘Statement’ rather than a ‘Theorem’ since it has not yet appeared in print. For further discussion of this result and related statements, see [Reference Mirzakhani and WrightMiWr, Conj. 2.10] and [Reference Chen and WrightChWr, §7].
6. Proof of main result
Using Statement A and further work of Wright [Reference WrightWr2], we can prove our main result.
Proof of Theorem 1.2.
Let
![]() $Z_0 = \mathrm {span}_{{\mathbb {R}}}(z_0)$
be a one-dimensional connected real Rel subgroup. Assume that (1) fails, so that the action of
$Z_0 = \mathrm {span}_{{\mathbb {R}}}(z_0)$
be a one-dimensional connected real Rel subgroup. Assume that (1) fails, so that the action of
![]() $Z_0$
on
$Z_0$
on
![]() $\left ({{\mathcal L}}, m_{\mathcal {L}} \right )$
is not mixing of all orders. Then, by Proposition 3.6, it is not ergodic. Let
$\left ({{\mathcal L}}, m_{\mathcal {L}} \right )$
is not mixing of all orders. Then, by Proposition 3.6, it is not ergodic. Let
![]() $\theta $
be the relatively independent self-joining over
$\theta $
be the relatively independent self-joining over
![]() ${{\mathcal L}} /\!\!/ Z_0$
. Applying Propositions 3.3 and 3.4, we have that
${{\mathcal L}} /\!\!/ Z_0$
. Applying Propositions 3.3 and 3.4, we have that
![]() $\theta \neq m_{{{\mathcal L}}} \times m_{{{\mathcal L}}}$
and
$\theta \neq m_{{{\mathcal L}}} \times m_{{{\mathcal L}}}$
and
![]() $\Delta _{{{\mathcal L}}} \subset \mathrm {supp} \, \theta $
. Applying Proposition 4.2 and Statement A, we have that there is a G-invariant open subset U of full
$\Delta _{{{\mathcal L}}} \subset \mathrm {supp} \, \theta $
. Applying Proposition 4.2 and Statement A, we have that there is a G-invariant open subset U of full
![]() $\theta $
-measure such that
$\theta $
-measure such that
![]() $U \cap \mathrm {supp} \, \theta $
is contained in the isomorphic image of an affine complex-linear manifold whose (real) dimension is strictly smaller than
$U \cap \mathrm {supp} \, \theta $
is contained in the isomorphic image of an affine complex-linear manifold whose (real) dimension is strictly smaller than
![]() $2 \dim \bar {\mathcal {H}}$
, and
$2 \dim \bar {\mathcal {H}}$
, and
![]() $\theta $
is obtained from Lebesgue measure on this complex-linear manifold by the cone construction.
$\theta $
is obtained from Lebesgue measure on this complex-linear manifold by the cone construction.
We claim that the set
is of full measure for
![]() $(\pi _{1})_* \theta $
, where
$(\pi _{1})_* \theta $
, where
![]() $\pi _1 : {{\mathcal L}} \times {{\mathcal L}} \to {{\mathcal L}}$
is the projection onto the first factor. Indeed, the measure
$\pi _1 : {{\mathcal L}} \times {{\mathcal L}} \to {{\mathcal L}}$
is the projection onto the first factor. Indeed, the measure
![]() $\theta $
is invariant under
$\theta $
is invariant under
![]() $Z_0 \times \{ \mathrm {Id} \}$
, and hence, so is its support. Since
$Z_0 \times \{ \mathrm {Id} \}$
, and hence, so is its support. Since
![]() $Z_0$
acts by homeomorphisms where defined, and using property (v) in Theorem 5.1 and Statement A, we have that the set U is also
$Z_0$
acts by homeomorphisms where defined, and using property (v) in Theorem 5.1 and Statement A, we have that the set U is also
![]() $Z_{0} \times \{\mathrm {Id}\}$
-invariant. Thus, for any
$Z_{0} \times \{\mathrm {Id}\}$
-invariant. Thus, for any
![]() $Z_{0}$
-ergodic measure, it is either null or conull. Thus, if
$Z_{0}$
-ergodic measure, it is either null or conull. Thus, if
![]() $q \notin U_1$
and q is generic for the measure
$q \notin U_1$
and q is generic for the measure
![]() $\mu _{T(q)}$
appearing in (3.1), then
$\mu _{T(q)}$
appearing in (3.1), then
![]() $\mu _{T(q),q}$
assigns measure zero to U, where
$\mu _{T(q),q}$
assigns measure zero to U, where
![]() $\mu _{T(q),q}$
is the measure on
$\mu _{T(q),q}$
is the measure on
![]() $\mathrm {supp}\, \theta $
defined by
$\mathrm {supp}\, \theta $
defined by
![]() $\mu _{T(q),q}(A)=\mu _{T(q)}(\{q':(q',q) \in A\})$
. If this were to happen for a positive measure of q, it would follow from (3.1) and the fact that
$\mu _{T(q),q}(A)=\mu _{T(q)}(\{q':(q',q) \in A\})$
. If this were to happen for a positive measure of q, it would follow from (3.1) and the fact that
![]() $\mu _{T(q)}\times \mu _{T(q)}=\int \mu _{T(q'),q'}d\mu _{T(q)}$
that U does not have full measure for
$\mu _{T(q)}\times \mu _{T(q)}=\int \mu _{T(q'),q'}d\mu _{T(q)}$
that U does not have full measure for
![]() $\theta $
.
$\theta $
.
For
![]() $q \in U_1$
, let
$q \in U_1$
, let
![]() $N_q$
denote the connected component of
$N_q$
denote the connected component of
![]() $ U \cap \pi _1^{-1}(q) \cap \mathrm {supp} \, \theta $
containing
$ U \cap \pi _1^{-1}(q) \cap \mathrm {supp} \, \theta $
containing
![]() $(q,q)$
. Recall from item (ii) of Theorem 5.1 that
$(q,q)$
. Recall from item (ii) of Theorem 5.1 that
![]() ${{\mathcal L}}$
is locally the intersection of
${{\mathcal L}}$
is locally the intersection of
![]() $\bar {{\mathcal L}} = \varphi (\mathcal {N})$
, a
$\bar {{\mathcal L}} = \varphi (\mathcal {N})$
, a
![]() $\mathbb {C}$
-linear subset of
$\mathbb {C}$
-linear subset of
![]() $\bar {\mathcal {H}}$
, with the quadric hypersurface
$\bar {\mathcal {H}}$
, with the quadric hypersurface
![]() ${\mathcal {H}}$
consisting of surfaces of unit area. In this proof, we will call such a subset an affine submanifold of
${\mathcal {H}}$
consisting of surfaces of unit area. In this proof, we will call such a subset an affine submanifold of
![]() ${\mathcal {H}}$
. Similarly, we will say that a subset of
${\mathcal {H}}$
. Similarly, we will say that a subset of
![]() ${{\mathcal L}} \times {{\mathcal L}}$
is an affine submanifold if it is locally the intersection of a
${{\mathcal L}} \times {{\mathcal L}}$
is an affine submanifold if it is locally the intersection of a
![]() $\mathbb {C}$
-linear subset of
$\mathbb {C}$
-linear subset of
![]() $\bar {\mathcal {H}} \times \bar {\mathcal {H}}$
with
$\bar {\mathcal {H}} \times \bar {\mathcal {H}}$
with
![]() ${\mathcal {H}} \times {\mathcal {H}}$
. Since the fibers
${\mathcal {H}} \times {\mathcal {H}}$
. Since the fibers
![]() $\pi _1^{-1}(q)$
are also affine submanifolds of
$\pi _1^{-1}(q)$
are also affine submanifolds of
![]() ${{\mathcal L}} \times {{\mathcal L}}$
, we have that the
${{\mathcal L}} \times {{\mathcal L}}$
, we have that the
![]() $N_q$
are affine submanifolds contained in
$N_q$
are affine submanifolds contained in
![]() $\pi _1^{-1}(q) \cong {{\mathcal L}}$
, so we can identify them with invariant submanifolds in
$\pi _1^{-1}(q) \cong {{\mathcal L}}$
, so we can identify them with invariant submanifolds in
![]() ${{\mathcal L}}$
(which we continue to denote by
${{\mathcal L}}$
(which we continue to denote by
![]() $N_q)$
. With this notation, we have
$N_q)$
. With this notation, we have
![]() $q \in N_q$
.
$q \in N_q$
.
The mapping
![]() $q \mapsto T_q(N_q)$
is locally constant; that is, letting
$q \mapsto T_q(N_q)$
is locally constant; that is, letting
![]() $V \subset \bar {\mathcal {H}}$
and
$V \subset \bar {\mathcal {H}}$
and
![]() $\mathcal {V} \subset \bar {\mathcal {H}}_{\mathrm {m}}$
be open sets such that
$\mathcal {V} \subset \bar {\mathcal {H}}_{\mathrm {m}}$
be open sets such that
![]() $\pi |_{\mathcal {V}}: \mathcal {V} \to V$
is a homeomorphism and
$\pi |_{\mathcal {V}}: \mathcal {V} \to V$
is a homeomorphism and
![]() $q \in V$
, the map
$q \in V$
, the map
![]() $q \mapsto \mathrm {dev} \circ \pi |_{\mathcal {V}}^{-1} (q) $
sends a neighborhood of q in
$q \mapsto \mathrm {dev} \circ \pi |_{\mathcal {V}}^{-1} (q) $
sends a neighborhood of q in
![]() $N_q$
to an affine subspace
$N_q$
to an affine subspace
![]() $W = W_{q, \mathcal {V}}$
of
$W = W_{q, \mathcal {V}}$
of
![]() $H^1(S, \Sigma; {\mathbb {R}}^2)$
, and the linear subspaces tangent to W are the same for all
$H^1(S, \Sigma; {\mathbb {R}}^2)$
, and the linear subspaces tangent to W are the same for all
![]() $q \in V$
. Since
$q \in V$
. Since
![]() $m_{{{\mathcal L}}} \times m_{{{\mathcal L}}}$
is the unique P-invariant ergodic measure on
$m_{{{\mathcal L}}} \times m_{{{\mathcal L}}}$
is the unique P-invariant ergodic measure on
![]() ${{\mathcal L}} \times {{\mathcal L}}$
of full support, we have
${{\mathcal L}} \times {{\mathcal L}}$
of full support, we have
![]() $\dim N_q < \dim {{\mathcal L}}$
for every
$\dim N_q < \dim {{\mathcal L}}$
for every
![]() $q \in U_1$
.
$q \in U_1$
.
Let
![]() $\bar \pi _1: \bar {\mathcal {H}} \times \bar {\mathcal {H}}$
denote the projection on the first factor, let
$\bar \pi _1: \bar {\mathcal {H}} \times \bar {\mathcal {H}}$
denote the projection on the first factor, let
![]() $\bar N_q$
denote the connected component of
$\bar N_q$
denote the connected component of
![]() $U \cap \bar \pi _1^{-1}(q) \cap \bar {{\mathcal L}} $
containing
$U \cap \bar \pi _1^{-1}(q) \cap \bar {{\mathcal L}} $
containing
![]() $(q,q)$
, and let
$(q,q)$
, and let
(the tangent space to
![]() $\bar N_q$
at q, thought of as a subset of the tangent space
$\bar N_q$
at q, thought of as a subset of the tangent space
![]() $T_q(\bar {{\mathcal L}})$
). That is, surfaces in
$T_q(\bar {{\mathcal L}})$
). That is, surfaces in
![]() $\bar N_q$
are obtained by moving locally in the affine space W defining
$\bar N_q$
are obtained by moving locally in the affine space W defining
![]() $\theta $
, as in item (iv) of Theorem 5.1, without requiring that the surfaces in
$\theta $
, as in item (iv) of Theorem 5.1, without requiring that the surfaces in
![]() $\bar N_q$
have area one. Then we either have
$\bar N_q$
have area one. Then we either have
![]() $\dim \bar N_q = \dim N_q$
or
$\dim \bar N_q = \dim N_q$
or
![]() $\dim \bar N_q = \dim N_q+1$
, depending on whether or not moving in W can change the area of a surface. The assignment
$\dim \bar N_q = \dim N_q+1$
, depending on whether or not moving in W can change the area of a surface. The assignment
![]() $q\mapsto \mathfrak {N}_q $
defines a proper flat sub-bundle of the tangent bundle
$q\mapsto \mathfrak {N}_q $
defines a proper flat sub-bundle of the tangent bundle
![]() $T(\bar {{\mathcal L}})$
. Flat sub-bundles of
$T(\bar {{\mathcal L}})$
. Flat sub-bundles of
![]() $T(\bar {{\mathcal L}})$
were classified in [Reference WrightWr2]. According to [Reference WrightWr2, Thm. 5.1],
$T(\bar {{\mathcal L}})$
were classified in [Reference WrightWr2]. According to [Reference WrightWr2, Thm. 5.1],
![]() $\mathfrak {N}_q \subset \mathfrak {R}_{{{\mathcal L}}}$
for each q, and
$\mathfrak {N}_q \subset \mathfrak {R}_{{{\mathcal L}}}$
for each q, and
![]() $\mathfrak {N}_q$
is a complex linear subspace which is locally constant. Since
$\mathfrak {N}_q$
is a complex linear subspace which is locally constant. Since
![]() $\mathfrak {R}_{{{\mathcal L}}}$
is acted on trivially by monodromy, we in fact have that
$\mathfrak {R}_{{{\mathcal L}}}$
is acted on trivially by monodromy, we in fact have that
![]() $\mathfrak {N}_q$
is independent of q, and we denote it by
$\mathfrak {N}_q$
is independent of q, and we denote it by
![]() $\mathfrak {R}_1$
. The leaves
$\mathfrak {R}_1$
. The leaves
![]() $\mathfrak {R}_1(q)$
coincide with
$\mathfrak {R}_1(q)$
coincide with
![]() $\bar N_q$
for each q since
$\bar N_q$
for each q since
![]() $\bar N_q$
is connected and of the same dimension. Since Rel deformations do not affect the area of the surface, we see that
$\bar N_q$
is connected and of the same dimension. Since Rel deformations do not affect the area of the surface, we see that
![]() $\bar {N}_q = N_q$
. In particular,
$\bar {N}_q = N_q$
. In particular,
![]() $\mathfrak {R}(q)$
is closed for each q.
$\mathfrak {R}(q)$
is closed for each q.
By (3.1), for a.e. q,
![]() $N_q$
is a connected component of the support of the ergodic component
$N_q$
is a connected component of the support of the ergodic component
![]() $(m_{{{\mathcal L}}})_q$
, which is a probability measure, and in particular,
$(m_{{{\mathcal L}}})_q$
, which is a probability measure, and in particular,
Since
![]() $Z_0$
acts ergodically with respect to
$Z_0$
acts ergodically with respect to
![]() $(m_{{{\mathcal L}}})_q$
, we have that almost surely
$(m_{{{\mathcal L}}})_q$
, we have that almost surely
![]() $N_q =\mathfrak {R}(q)$
. Since the measure
$N_q =\mathfrak {R}(q)$
. Since the measure
![]() $(m_{{{\mathcal L}}})_q$
is affine in charts, it is a scalar multiple of the translation-invariant measure on
$(m_{{{\mathcal L}}})_q$
is affine in charts, it is a scalar multiple of the translation-invariant measure on
![]() $\mathfrak {R}(q)$
, and thus, the volume
$\mathfrak {R}(q)$
, and thus, the volume
![]() $V_q$
of
$V_q$
of
![]() $\mathfrak {R}(q)$
(with respect to its translation-invariant measure) is almost surely finite. It is clear that the function
$\mathfrak {R}(q)$
(with respect to its translation-invariant measure) is almost surely finite. It is clear that the function
![]() $q \mapsto V_q$
is U-invariant, and by ergodicity, it is constant almost surely. Thus, assertion (2) of Theorem 1.2 holds, with
$q \mapsto V_q$
is U-invariant, and by ergodicity, it is constant almost surely. Thus, assertion (2) of Theorem 1.2 holds, with
![]() $Z_1 = \mathfrak {R}_1 \cap Z_{{{\mathcal L}}}$
.
$Z_1 = \mathfrak {R}_1 \cap Z_{{{\mathcal L}}}$
.
Remark 6.1. We note that the above argument works under much weaker conclusions than those given in Statement A. Indeed, in the first step of the argument, Statement A was used simply to extract a G-invariant assignment
![]() $q \mapsto N_q$
, where
$q \mapsto N_q$
, where
![]() $N_q$
is a subspace of
$N_q$
is a subspace of
![]() $T_q({{\mathcal L}})$
, which is proper if
$T_q({{\mathcal L}})$
, which is proper if
![]() $\theta $
is not the product joining. A fundamental fact about such G-invariant assignments is that they are very restricted – besides [Reference WrightWr2], see [Reference Eskin, Filip and WrightEFW] and [Reference FilipFi]. In particular, [Reference FilipFi] gives strong restrictions on assignments that are only assumed to be defined almost everywhere and measurable.
$\theta $
is not the product joining. A fundamental fact about such G-invariant assignments is that they are very restricted – besides [Reference WrightWr2], see [Reference Eskin, Filip and WrightEFW] and [Reference FilipFi]. In particular, [Reference FilipFi] gives strong restrictions on assignments that are only assumed to be defined almost everywhere and measurable.
7. A topological condition for Rel ergodicity
Let
![]() $Z_0 \subset Z$
be a subspace. We say that a translation surface x is
$Z_0 \subset Z$
be a subspace. We say that a translation surface x is
![]() $Z_0$
-stably periodic if it can be presented as a finite union of horizontal cylinders and the
$Z_0$
-stably periodic if it can be presented as a finite union of horizontal cylinders and the
![]() $Z_0$
-orbit of x is well defined. Recall that a horizontal separatrix is a horizontal leaf whose closure contains at least one singularity, and it is a horizontal saddle connection if its closure contains two singularities. Then the condition of being
$Z_0$
-orbit of x is well defined. Recall that a horizontal separatrix is a horizontal leaf whose closure contains at least one singularity, and it is a horizontal saddle connection if its closure contains two singularities. Then the condition of being
![]() $Z_ 0$
-stably periodic is equivalent to requiring that all horizontal separatrices starting at singular points are on horizontal saddle connections, and
$Z_ 0$
-stably periodic is equivalent to requiring that all horizontal separatrices starting at singular points are on horizontal saddle connections, and
![]() $Z_0$
preserves the holonomy of every horizontal saddle connection on x. In case
$Z_0$
preserves the holonomy of every horizontal saddle connection on x. In case
![]() $Z =Z_0$
is the full real Rel group, we say that x is fully stably periodic. This is equivalent to saying that all horizontal separatrices starting at singular points are on saddle connections, and all horizontal saddle connections start and end at the same singularity. In particular, for any cylinder C on a fully stably periodic surface, each boundary component of C is made of saddle connections starting and ending at the same singular point
$Z =Z_0$
is the full real Rel group, we say that x is fully stably periodic. This is equivalent to saying that all horizontal separatrices starting at singular points are on saddle connections, and all horizontal saddle connections start and end at the same singularity. In particular, for any cylinder C on a fully stably periodic surface, each boundary component of C is made of saddle connections starting and ending at the same singular point
![]() $\xi $
; we say that the boundary component only sees singularity
$\xi $
; we say that the boundary component only sees singularity
![]() $\xi $
. For more information on the real Rel action on surfaces which are horizontally completely periodic, see [Reference Hooper and WeissHW, §6.1].
$\xi $
. For more information on the real Rel action on surfaces which are horizontally completely periodic, see [Reference Hooper and WeissHW, §6.1].
Proposition 7.1. Suppose x is a surface which is
![]() $Z_0$
-stably periodic, and
$Z_0$
-stably periodic, and
![]() $v \in Z_0$
moves two singularities p and q with respect to each other. Suppose that x contains two cylinders
$v \in Z_0$
moves two singularities p and q with respect to each other. Suppose that x contains two cylinders
![]() $C_1$
and
$C_1$
and
![]() $C_2$
that both only see singularity p on one boundary component and only see singularity q on another boundary component. Finally, suppose the circumferences
$C_2$
that both only see singularity p on one boundary component and only see singularity q on another boundary component. Finally, suppose the circumferences
![]() $c_1, c_2$
of these cylinders satisfy
$c_1, c_2$
of these cylinders satisfy
![]() $\frac {c_1}{c_2} \notin {\mathbb {Q}}$
. Then Case (2) of Theorem 1.1 does not hold for x.
$\frac {c_1}{c_2} \notin {\mathbb {Q}}$
. Then Case (2) of Theorem 1.1 does not hold for x.
Proof. Since
![]() $\frac {c_1}{c_2} \notin {\mathbb {Q}}$
, the trajectory
$\frac {c_1}{c_2} \notin {\mathbb {Q}}$
, the trajectory
![]() $\{{\mathrm {Rel}}_{tv}(x) : t \in {\mathbb {R}}\}$
is not closed, let
$\{{\mathrm {Rel}}_{tv}(x) : t \in {\mathbb {R}}\}$
is not closed, let
![]() $\mathcal {L}$
denote its closure. We claim that the tangent space to
$\mathcal {L}$
denote its closure. We claim that the tangent space to
![]() $\mathcal {L}$
is not contained in Z. Let
$\mathcal {L}$
is not contained in Z. Let
![]() $\sigma _1$
denote a saddle connection from p to q in
$\sigma _1$
denote a saddle connection from p to q in
![]() $C_1$
and let
$C_1$
and let
![]() $\sigma _2$
denote a saddle connection from q to p in
$\sigma _2$
denote a saddle connection from q to p in
![]() $C_2$
. Let
$C_2$
. Let
![]() $\sigma $
be the concatenation. Then
$\sigma $
be the concatenation. Then
![]() $\sigma $
represents an absolute homology class because it goes from p back to p, and it is nontrivial because the vertical component of its holonomy on x is nonzero. If we consider the restriction of the rel-action to
$\sigma $
represents an absolute homology class because it goes from p back to p, and it is nontrivial because the vertical component of its holonomy on x is nonzero. If we consider the restriction of the rel-action to
![]() $C_1 \cup C_2$
, then it only affects the twist parameters, which is a 2-dimensional space. This space can be generated by the horizontal holonomy of
$C_1 \cup C_2$
, then it only affects the twist parameters, which is a 2-dimensional space. This space can be generated by the horizontal holonomy of
![]() $\sigma _1$
and the horizontal holonomy of
$\sigma _1$
and the horizontal holonomy of
![]() $\sigma _2$
. Since
$\sigma _2$
. Since
![]() $\frac {c_1}{c_2} \notin {\mathbb {Q}}$
, this restricted action does not give a closed orbit. So the tangent space to
$\frac {c_1}{c_2} \notin {\mathbb {Q}}$
, this restricted action does not give a closed orbit. So the tangent space to
![]() $\mathcal {L}$
contains directions, which continuously affect the holonomy of
$\mathcal {L}$
contains directions, which continuously affect the holonomy of
![]() $\sigma $
. Since
$\sigma $
. Since
![]() $\sigma $
is an absolute period, we see that the tangent space to
$\sigma $
is an absolute period, we see that the tangent space to
![]() $\mathcal {L}$
is not contained in Z.
$\mathcal {L}$
is not contained in Z.
8. Checking the condition for strata
Let
![]() ${\mathcal {H}} = {\mathcal {H}}(a_1, \ldots , a_k)$
, and for
${\mathcal {H}} = {\mathcal {H}}(a_1, \ldots , a_k)$
, and for
![]() $i, j \in \{1, \ldots , k\}$
, let
$i, j \in \{1, \ldots , k\}$
, let
![]() $\xi _i, \xi _j$
be the corresponding singular points of a surface in
$\xi _i, \xi _j$
be the corresponding singular points of a surface in
![]() ${\mathcal {H}}$
. Let
${\mathcal {H}}$
. Let
![]() $z \in \mathfrak {R}$
be a Rel cohomology class. We say that z moves
$z \in \mathfrak {R}$
be a Rel cohomology class. We say that z moves
![]() $\xi _i, \xi _j$
with respect to each other if for some (equivalently, every)
$\xi _i, \xi _j$
with respect to each other if for some (equivalently, every)
![]() $\alpha \in H_1(S, \Sigma )$
represented by a path starting at
$\alpha \in H_1(S, \Sigma )$
represented by a path starting at
![]() $\xi _i$
and ending at
$\xi _i$
and ending at
![]() $\xi _j$
, we have
$\xi _j$
, we have
![]() $z(\alpha ) \neq 0$
. Below, when we discuss a stratum
$z(\alpha ) \neq 0$
. Below, when we discuss a stratum
![]() ${\mathcal {H}}(a_1, \ldots , a_k)$
; we allow
${\mathcal {H}}(a_1, \ldots , a_k)$
; we allow
![]() $a_i=0$
; that is, we allow marked points. We call points with cone angle
$a_i=0$
; that is, we allow marked points. We call points with cone angle
![]() $2\pi $
(that is, with
$2\pi $
(that is, with
![]() $a=0$
) removable singularities, and otherwise, we call them non-removable. The following result, which clearly implies Theorem 1.1, allows strata with removable singularities.
$a=0$
) removable singularities, and otherwise, we call them non-removable. The following result, which clearly implies Theorem 1.1, allows strata with removable singularities.
Theorem 8.1. Let
![]() ${{\mathcal {H}}}$
be a connected component of a stratum
${{\mathcal {H}}}$
be a connected component of a stratum
![]() ${{\mathcal {H}}}(a_1, \ldots , a_k)$
. Let
${{\mathcal {H}}}(a_1, \ldots , a_k)$
. Let
![]() $m_{{\mathcal {H}}}$
be the Masur-Veech measure on
$m_{{\mathcal {H}}}$
be the Masur-Veech measure on
![]() ${{\mathcal {H}}}$
, let Z be the corresponding real Rel foliation, and let
${{\mathcal {H}}}$
, let Z be the corresponding real Rel foliation, and let
![]() $Z_0 \subset Z$
be a one-dimensional connected subgroup of Z. Suppose that there are
$Z_0 \subset Z$
be a one-dimensional connected subgroup of Z. Suppose that there are
![]() $1 \leq i < j \leq k$
with corresponding singular points
$1 \leq i < j \leq k$
with corresponding singular points
![]() $\xi _i, \xi _j$
, such that
$\xi _i, \xi _j$
, such that
![]() $a_i>0, \, a_j>0$
and such that some element of
$a_i>0, \, a_j>0$
and such that some element of
![]() $Z_0$
moves
$Z_0$
moves
![]() $\xi _i, \xi _j$
with respect to each other. Then the
$\xi _i, \xi _j$
with respect to each other. Then the
![]() $Z_0$
-flow on
$Z_0$
-flow on
![]() $({{\mathcal {H}}}, m_{{{\mathcal {H}}}})$
is mixing of all orders (and in particular, ergodic).
$({{\mathcal {H}}}, m_{{{\mathcal {H}}}})$
is mixing of all orders (and in particular, ergodic).
Clearly, Theorem 8.1 follows from Theorem 1.2, Proposition 7.1 and the following result.
Proposition 8.2. Let
![]() ${\mathcal {H}} \subset {\mathcal {H}}(a_1,\ldots ,a_k)$
be a connected component of a stratum of translation surfaces with at least two non-removable singular points. If
${\mathcal {H}} \subset {\mathcal {H}}(a_1,\ldots ,a_k)$
be a connected component of a stratum of translation surfaces with at least two non-removable singular points. If
![]() $p\neq q$
is any pair of non-removable singularities, then there exists
$p\neq q$
is any pair of non-removable singularities, then there exists
![]() $M \in {\mathcal {H}}$
, which has cylinders
$M \in {\mathcal {H}}$
, which has cylinders
![]() $C_1,C_2$
with circumferences
$C_1,C_2$
with circumferences
![]() $c_1,c_2$
so that
$c_1,c_2$
so that
-
(1) M is fully stably periodic.
-
(2)
 $\frac {c_1}{c_2} \notin \mathbb {Q}$
.
$\frac {c_1}{c_2} \notin \mathbb {Q}$
. -
(3) Both
 $C_1$
and
$C_1$
and
 $C_2$
only see singularity p on one boundary component and only see singularity q on the other boundary component.
$C_2$
only see singularity p on one boundary component and only see singularity q on the other boundary component.
For the proof of Proposition 8.2, we will also need the following:
Proposition 8.3. Let
![]() ${\mathcal {H}} = {\mathcal {H}}(a_1,\ldots ,a_k)$
be a stratum of translation surfaces with at least two singular points (that is
${\mathcal {H}} = {\mathcal {H}}(a_1,\ldots ,a_k)$
be a stratum of translation surfaces with at least two singular points (that is
![]() $k\geq 2$
). If
$k\geq 2$
). If
![]() $p\neq q$
is any pair of distinct singularities (possibly removable), then there exists
$p\neq q$
is any pair of distinct singularities (possibly removable), then there exists
![]() $M \in {\mathcal {H}}$
, so that M is fully stably periodic and there exists a cylinder on M that only sees singularity p on one boundary component, and only sees singularity q on the other boundary component.
$M \in {\mathcal {H}}$
, so that M is fully stably periodic and there exists a cylinder on M that only sees singularity p on one boundary component, and only sees singularity q on the other boundary component.
Propositions 8.2 and 8.3 will both be proved by induction, after some preparations.
Lemma 8.4 (The basic surgery – gluing in a torus).
Let
![]() ${\mathcal {H}} = {\mathcal {H}}(b_1, \ldots ,b_{\ell })$
be a stratum of translation surfaces, and let
${\mathcal {H}} = {\mathcal {H}}(b_1, \ldots ,b_{\ell })$
be a stratum of translation surfaces, and let
![]() $M \in {\mathcal {H}}$
, with singularities labeled by
$M \in {\mathcal {H}}$
, with singularities labeled by
![]() $\xi _1, \ldots , \xi _\ell $
, so that the order of
$\xi _1, \ldots , \xi _\ell $
, so that the order of
![]() $\xi _i$
is
$\xi _i$
is
![]() $b_i$
. Suppose M has a horizontal cylinder C, with circumference c, where one boundary component is made of saddle connections that begin and end at
$b_i$
. Suppose M has a horizontal cylinder C, with circumference c, where one boundary component is made of saddle connections that begin and end at
![]() $\xi _i$
, and the other is made of saddle connections that begin and end at
$\xi _i$
, and the other is made of saddle connections that begin and end at
![]() $\xi _j$
, where
$\xi _j$
, where
![]() $b_i \geq 0$
and
$b_i \geq 0$
and
![]() $b_j \geq 0$
(so that
$b_j \geq 0$
(so that
![]() $\xi _i, \xi _j$
might be removable). Then for all
$\xi _i, \xi _j$
might be removable). Then for all
![]() $w>0$
, there exists
$w>0$
, there exists
![]() $M' \in {\mathcal {H}}(b_1, \ldots ,b_{i}+1, \ldots ,b_{j}+1, \ldots ,b_\ell )$
, with singularities labeled
$M' \in {\mathcal {H}}(b_1, \ldots ,b_{i}+1, \ldots ,b_{j}+1, \ldots ,b_\ell )$
, with singularities labeled
![]() $\xi ^{\prime }_1, \ldots , \xi ^{\prime }_\ell $
, which has two horizontal cylinders
$\xi ^{\prime }_1, \ldots , \xi ^{\prime }_\ell $
, which has two horizontal cylinders
![]() $C^{\prime }_1$
,
$C^{\prime }_1$
,
![]() $C^{\prime }_2$
, where
$C^{\prime }_2$
, where
![]() $C^{\prime }_1$
has circumference
$C^{\prime }_1$
has circumference
![]() $c+w$
and
$c+w$
and
![]() $C^{\prime }_2$
has circumference w. The complements
$C^{\prime }_2$
has circumference w. The complements
![]() $M \smallsetminus C$
and
$M \smallsetminus C$
and
![]() $M' \smallsetminus (C_1 \cup C_2)$
are isometric by an isometry mapping
$M' \smallsetminus (C_1 \cup C_2)$
are isometric by an isometry mapping
![]() $\xi ^{\prime }_i$
to
$\xi ^{\prime }_i$
to
![]() $\xi _i$
for all i. The cylinders
$\xi _i$
for all i. The cylinders
![]() $C_1$
and
$C_1$
and
![]() $C_2$
only see singularity
$C_2$
only see singularity
![]() $\xi ^{\prime }_i$
on one boundary component, and
$\xi ^{\prime }_i$
on one boundary component, and
![]() $\xi ^{\prime }_j$
on another. Moreover, if M is fully stably periodic, then so is
$\xi ^{\prime }_j$
on another. Moreover, if M is fully stably periodic, then so is
![]() $M'$
.
$M'$
.
Proof. It will be easier to follow the proof while consulting Figures 1 (before) and 2 (after). Given a polygonal presentation for M, we give a polygonal presentation for
![]() $M'$
. Let M be a polygon representation for M in which the cylinder C is represented by a parallelogram P (in Figure 1, the large rectangle in the center of the presentation), with two horizontal sides of length c, nonhorizontal sides identified to each other, and the singular points
$M'$
. Let M be a polygon representation for M in which the cylinder C is represented by a parallelogram P (in Figure 1, the large rectangle in the center of the presentation), with two horizontal sides of length c, nonhorizontal sides identified to each other, and the singular points
![]() $\xi _i$
,
$\xi _i$
,
![]() $\xi _j$
on adjacent corners of P. Thus, the nonhorizontal sides of P represent a saddle connection
$\xi _j$
on adjacent corners of P. Thus, the nonhorizontal sides of P represent a saddle connection
![]() $\sigma $
on M connecting
$\sigma $
on M connecting
![]() $\xi _i$
to
$\xi _i$
to
![]() $\xi _j$
. We consider the two nonhorizontal sides of P as distinct and label them by
$\xi _j$
. We consider the two nonhorizontal sides of P as distinct and label them by
![]() $\sigma _1, \sigma _2$
. Let
$\sigma _1, \sigma _2$
. Let
![]() $P'$
be a parallelogram with sides parallel to those of P, where the horizontal sides have length w and the nonhorizontal sides are longer than the ones on P (in Figure 2,
$P'$
be a parallelogram with sides parallel to those of P, where the horizontal sides have length w and the nonhorizontal sides are longer than the ones on P (in Figure 2,
![]() $P'$
is to the right of P).
$P'$
is to the right of P).
Figure 1 The surface M has a cylinder of circumference c, and its boundary components see only the singularities
![]() $\xi _i$
and
$\xi _i$
and
![]() $\xi _j$
(denoted by
$\xi _j$
(denoted by
![]() $\circ $
and
$\circ $
and
![]() $\bullet $
). The edges not labeled by
$\bullet $
). The edges not labeled by
![]() $\triangle $
are connected to
$\triangle $
are connected to
![]() $M \smallsetminus C$
.
$M \smallsetminus C$
.
Figure 2 To obtain
![]() $M'$
from M, glue in a torus (rectangle on the right). This transforms C into a cylinder
$M'$
from M, glue in a torus (rectangle on the right). This transforms C into a cylinder
![]() $C^{\prime }_1$
of circumference
$C^{\prime }_1$
of circumference
![]() $c+w$
, and adds a horizontal cylinder
$c+w$
, and adds a horizontal cylinder
![]() $C^{\prime }_2$
of circumference w. Edges not labeled by
$C^{\prime }_2$
of circumference w. Edges not labeled by
![]() $\triangle $
,
$\triangle $
,
![]() $\square $
, / or the color green are attached to
$\square $
, / or the color green are attached to
![]() $M' \smallsetminus (C^{\prime }_1 \cup C^{\prime }_2)$
.
$M' \smallsetminus (C^{\prime }_1 \cup C^{\prime }_2)$
.
Label the two horizontal sides of
![]() $P'$
by
$P'$
by
![]() $h^{\prime }_1$
and
$h^{\prime }_1$
and
![]() $h^{\prime }_2$
, and identify them by a translation. Partition the nonhorizontal sides of
$h^{\prime }_2$
, and identify them by a translation. Partition the nonhorizontal sides of
![]() $P'$
into two segments. The segments
$P'$
into two segments. The segments
![]() $\sigma ^{\prime }_1, \sigma ^{\prime }_2$
are parallel to each other and have the same length as
$\sigma ^{\prime }_1, \sigma ^{\prime }_2$
are parallel to each other and have the same length as
![]() $\sigma _1, \sigma _2$
and start at a corner of P. The segments
$\sigma _1, \sigma _2$
and start at a corner of P. The segments
![]() $\gamma ^{\prime }_1, \gamma ^{\prime }_2$
comprise the remainder of the nonhorizontal sides of
$\gamma ^{\prime }_1, \gamma ^{\prime }_2$
comprise the remainder of the nonhorizontal sides of
![]() $P'$
(and in particular, have the same length). Identify
$P'$
(and in particular, have the same length). Identify
![]() $\gamma ^{\prime }_1$
to
$\gamma ^{\prime }_1$
to
![]() $\gamma ^{\prime }_2$
by a translation, and identify
$\gamma ^{\prime }_2$
by a translation, and identify
![]() $\sigma ^{\prime }_1, \sigma ^{\prime }_2$
to
$\sigma ^{\prime }_1, \sigma ^{\prime }_2$
to
![]() $\sigma _1, \sigma _2$
by a translation so that each
$\sigma _1, \sigma _2$
by a translation so that each
![]() $\sigma ^{\prime }_i$
is attached to the
$\sigma ^{\prime }_i$
is attached to the
![]() $\sigma _j$
with the opposite orientation. Let
$\sigma _j$
with the opposite orientation. Let
![]() $M'$
be the translation surface corresponding to this presentation. It is clear that
$M'$
be the translation surface corresponding to this presentation. It is clear that
![]() $M'$
has the required properties.
$M'$
has the required properties.
Proof of Proposition 8.3.
The proof is by induction on
![]() $\sum a_i$
.
$\sum a_i$
.
Base of induction: The base case is the stratum
![]() ${{\mathcal {H}}}(a_1, 0^{s})$
– that is, one singular point (removable or non-removable) of order
${{\mathcal {H}}}(a_1, 0^{s})$
– that is, one singular point (removable or non-removable) of order
![]() $a_1$
, and some number
$a_1$
, and some number
![]() $s \geq 1$
of removable singular points. In this case, we take a surface in
$s \geq 1$
of removable singular points. In this case, we take a surface in
![]() ${{\mathcal {H}}}(a_1)$
which is made of one horizontal cylinder. We label the singular point by
${{\mathcal {H}}}(a_1)$
which is made of one horizontal cylinder. We label the singular point by
![]() $\xi _1$
and place additional removable singular points
$\xi _1$
and place additional removable singular points
![]() $\xi _2, \ldots , \xi _{s+1}$
in the interior of the cylinder, at different heights (so that the resulting surface has no horizontal saddle connections between distinct singularities) and so that
$\xi _2, \ldots , \xi _{s+1}$
in the interior of the cylinder, at different heights (so that the resulting surface has no horizontal saddle connections between distinct singularities) and so that
![]() $\xi _i$
and
$\xi _i$
and
![]() $\xi _j$
are on opposite sides of a cylinder.
$\xi _j$
are on opposite sides of a cylinder.
Inductive step: Suppose
![]() ${{\mathcal {H}}}' = {{\mathcal {H}}}(a_1, \ldots , a_k)$
is our stratum, where at least two of the singularities are non-removable. Let
${{\mathcal {H}}}' = {{\mathcal {H}}}(a_1, \ldots , a_k)$
is our stratum, where at least two of the singularities are non-removable. Let
![]() $p', q'$
be labels of singular points for surfaces in
$p', q'$
be labels of singular points for surfaces in
![]() ${{\mathcal {H}}}'$
, corresponding to indices
${{\mathcal {H}}}'$
, corresponding to indices
![]() $i \neq j$
. To simplify notation, assume
$i \neq j$
. To simplify notation, assume
![]() $i=1, j=2$
. There are three cases to consider:
$i=1, j=2$
. There are three cases to consider:
![]() $a_i = a_j=0$
, or one of
$a_i = a_j=0$
, or one of
![]() $a_i, a_j$
are positive, or both are positive.
$a_i, a_j$
are positive, or both are positive.
If
![]() $a_i = a_j=0$
, then by assumption,
$a_i = a_j=0$
, then by assumption,
![]() $k \geq 4$
. We take a cylinder C on a fully stably completely periodic surface M in
$k \geq 4$
. We take a cylinder C on a fully stably completely periodic surface M in
![]() ${{\mathcal {H}}} = {{\mathcal {H}}}(a_1, \ldots , \hat {a}_i, \ldots , \hat {a}_j, \ldots , a_k)$
. The notation
${{\mathcal {H}}} = {{\mathcal {H}}}(a_1, \ldots , \hat {a}_i, \ldots , \hat {a}_j, \ldots , a_k)$
. The notation
![]() $\hat {a}_i$
means that the symbol should be ignored – that is, on a stratum of the same genus with
$\hat {a}_i$
means that the symbol should be ignored – that is, on a stratum of the same genus with
![]() $k-2 \geq 2$
singular points obtained by removing two removable singular points. We place two singular points marked
$k-2 \geq 2$
singular points obtained by removing two removable singular points. We place two singular points marked
![]() $p', q'$
in the interior of C at different heights. If
$p', q'$
in the interior of C at different heights. If
![]() $a_i>0$
and
$a_i>0$
and
![]() $ a_j=0$
is zero, we take a fully stably periodic surface M in
$ a_j=0$
is zero, we take a fully stably periodic surface M in
![]() ${{\mathcal {H}}}(a_1, \ldots , a_i, \ldots , \hat {a}_j, \ldots , a_k)$
, find a cylinder C on M whose boundary component is made of saddle connections starting and ending at
${{\mathcal {H}}}(a_1, \ldots , a_i, \ldots , \hat {a}_j, \ldots , a_k)$
, find a cylinder C on M whose boundary component is made of saddle connections starting and ending at
![]() $\xi _i$
, and place a marked point labeled
$\xi _i$
, and place a marked point labeled
![]() $\xi _j$
in the interior of C. If
$\xi _j$
in the interior of C. If
![]() $a_i$
and
$a_i$
and
![]() $a_j$
are both positive, we use the induction hypothesis to find a surface
$a_j$
are both positive, we use the induction hypothesis to find a surface
![]() $M \in {{\mathcal {H}}}(a_1, \ldots , a_i-1, \ldots , a_j-1, \ldots , a_k)$
with a cylinder whose boundary components see
$M \in {{\mathcal {H}}}(a_1, \ldots , a_i-1, \ldots , a_j-1, \ldots , a_k)$
with a cylinder whose boundary components see
![]() $\xi _i$
and
$\xi _i$
and
![]() $\xi _j$
, and we perform the surgery in Lemma 8.4 to this cylinder.
$\xi _j$
, and we perform the surgery in Lemma 8.4 to this cylinder.
Lemma 8.5 (Two surgeries involving genus two surfaces).
Let
![]() ${{\mathcal {H}}} = {\mathcal {H}}(b_1, \ldots ,b_k)$
be a stratum of translation surfaces, and let
${{\mathcal {H}}} = {\mathcal {H}}(b_1, \ldots ,b_k)$
be a stratum of translation surfaces, and let
![]() $M \in {{\mathcal {H}}}$
have a horizontal cylinder C, with circumference c. Let p and q be singular points with order
$M \in {{\mathcal {H}}}$
have a horizontal cylinder C, with circumference c. Let p and q be singular points with order
![]() $b_i, b_j$
, respectively, such that one boundary component of C only sees singularity p and the other only sees singularity q. Then for any
$b_i, b_j$
, respectively, such that one boundary component of C only sees singularity p and the other only sees singularity q. Then for any
![]() $w_1,w_2>0$
, there exists
$w_1,w_2>0$
, there exists
![]() $M' \in {{\mathcal {H}}}' = {\mathcal {H}}(b_1, \ldots ,b_i+2, \ldots ,b_j+2, \ldots ,b_k)$
which has three cylinders
$M' \in {{\mathcal {H}}}' = {\mathcal {H}}(b_1, \ldots ,b_i+2, \ldots ,b_j+2, \ldots ,b_k)$
which has three cylinders
![]() $C_1, C_2, C_3$
with circumferences
$C_1, C_2, C_3$
with circumferences
![]() $c+w_1+w_2, w_1$
and
$c+w_1+w_2, w_1$
and
![]() $w_2$
, respectively. The complements
$w_2$
, respectively. The complements
![]() $M \smallsetminus C$
and
$M \smallsetminus C$
and
![]() $M' \smallsetminus (C_1 \cup C_2 \cup C_3)$
are isometric by an isometry preserving the labels of singular points, and
$M' \smallsetminus (C_1 \cup C_2 \cup C_3)$
are isometric by an isometry preserving the labels of singular points, and
![]() $C_1, C_2, C_3$
all have one boundary component that sees only p, and another that sees only q. Thus, if M is fully stably periodic, so is
$C_1, C_2, C_3$
all have one boundary component that sees only p, and another that sees only q. Thus, if M is fully stably periodic, so is
![]() $M'$
. Moreover, if the
$M'$
. Moreover, if the
![]() $b_i$
are all even, so that
$b_i$
are all even, so that
![]() ${{\mathcal {H}}}' $
has even and odd spin components, we can choose
${{\mathcal {H}}}' $
has even and odd spin components, we can choose
![]() $M'$
to be in either the even or odd connected component.
$M'$
to be in either the even or odd connected component.
Proof. Once again, we encourage the reader to consult Figures 3 and 4.

Figure 3 First option for
![]() $M'$
in Lemma 8.5. Attaching the subsurface on the right increases the genus by 2. Unlabeled edges are attached to
$M'$
in Lemma 8.5. Attaching the subsurface on the right increases the genus by 2. Unlabeled edges are attached to
![]() $M' \smallsetminus (C_1 \cup C_2 \cup C_3)$
.
$M' \smallsetminus (C_1 \cup C_2 \cup C_3)$
.
Figure 4 Second option for
![]() $M'$
, with a different spin.
$M'$
, with a different spin.
In Lemma 8.4, we made a slit in M, running through P from top to bottom, and glued in a torus with a slit. In this case, we make an identical slit, this time gluing in a genus two surface with a slit. This surface is presented in Figures 3 and 4 as made up of three rectangles. It is straightforward to check that
![]() $M' \in {{\mathcal {H}}}'$
and that it has cylinders satisfying the desired properties. It remains to check the final assertion about the parity of the spin structure.
$M' \in {{\mathcal {H}}}'$
and that it has cylinders satisfying the desired properties. It remains to check the final assertion about the parity of the spin structure.
Recall from [Reference Kontsevich and ZorichKZ, eqn. (4)] that where defined, the spin structure of a surface M of genus g can be computed as follows. Let
![]() $\alpha _i, \beta _j $
(where
$\alpha _i, \beta _j $
(where
![]() $1 \leq i,j \leq g$
) be a symplectic basis for
$1 \leq i,j \leq g$
) be a symplectic basis for
![]() $H_1(M)$
, realized explicitly as smooth curves on M. This means that all of these curves are disjoint, except for
$H_1(M)$
, realized explicitly as smooth curves on M. This means that all of these curves are disjoint, except for
![]() $\alpha _i$
and
$\alpha _i$
and
![]() $\beta _i$
which intersect once. For each curve
$\beta _i$
which intersect once. For each curve
![]() $\gamma $
, let
$\gamma $
, let
![]() $\mathrm {ind}(\gamma )$
be the turning index – that is, the total number of circles made by the tangent vector to
$\mathrm {ind}(\gamma )$
be the turning index – that is, the total number of circles made by the tangent vector to
![]() $\gamma $
, as one goes around
$\gamma $
, as one goes around
![]() $\gamma $
. The parity of M is then the parity of the integer
$\gamma $
. The parity of M is then the parity of the integer
![]() $\sum _{i=1}^g (1 +\mathrm {ind}(\alpha _i)) (1 +\mathrm {ind}(\beta _i)) $
. It is shown in [Reference Kontsevich and ZorichKZ] that this number is well defined (independent of the choice of the symplectic basis) when all the singular points have even order.
$\sum _{i=1}^g (1 +\mathrm {ind}(\alpha _i)) (1 +\mathrm {ind}(\beta _i)) $
. It is shown in [Reference Kontsevich and ZorichKZ] that this number is well defined (independent of the choice of the symplectic basis) when all the singular points have even order.

Figure 5 Modifying the symplectic basis. Gluings as in Figure 3.
Suppose M has genus g and is equipped with a symplectic basis. Since any non-separating simple closed curve can be completed to a symplectic basis, we can assume that
![]() $\alpha _1$
is the core curve of C, and the other curves in the basis do not intersect the saddle connection from p to q passing through C. We construct a symplectic basis for
$\alpha _1$
is the core curve of C, and the other curves in the basis do not intersect the saddle connection from p to q passing through C. We construct a symplectic basis for
![]() $M'$
in both cases, by modifying
$M'$
in both cases, by modifying
![]() $\alpha _1$
, keeping
$\alpha _1$
, keeping
![]() $\alpha _2, \ldots , \alpha _g, \beta _1, \ldots , \beta _g$
, and adding new curves
$\alpha _2, \ldots , \alpha _g, \beta _1, \ldots , \beta _g$
, and adding new curves
![]() $\alpha _{g+1}, \alpha _{g+2}, \beta _{g+1}, \beta _{g+2}$
. The modified curves are shown in Figures 5 and 6, and the reader can easily check that these new curves still form a symplectic basis and that these two choices add two numbers of different parities to the spin structure.
$\alpha _{g+1}, \alpha _{g+2}, \beta _{g+1}, \beta _{g+2}$
. The modified curves are shown in Figures 5 and 6, and the reader can easily check that these new curves still form a symplectic basis and that these two choices add two numbers of different parities to the spin structure.
Note that in Proposition 8.2, we care about all connected components of strata. We need to record some information about the classification of connected components of strata, due to Kontsevich and Zorich. A translation surface is hyperelliptic if it admits an involution which acts on absolute homology as
![]() $-\mathrm {Id}$
(see [Reference Farb and MargalitFM] or [Reference Kontsevich and ZorichKZ, §2.1] for more details). A connected component of a stratum is hyperelliptic if all surfaces in the component are hyperelliptic.
$-\mathrm {Id}$
(see [Reference Farb and MargalitFM] or [Reference Kontsevich and ZorichKZ, §2.1] for more details). A connected component of a stratum is hyperelliptic if all surfaces in the component are hyperelliptic.
Figure 6 Modifying the symplectic basis, second case. Gluings as in Figure 4. Note the change in the rotation number of
![]() $\beta _{g+2}$
.
$\beta _{g+2}$
.
Proposition 8.6 ([Reference Kontsevich and ZorichKZ], Theorems 1 & 5 and Corollary 5 of Appendix B).
Let
![]() ${{\mathcal {H}}}(a_1, \ldots , a_k)$
be a stratum with
${{\mathcal {H}}}(a_1, \ldots , a_k)$
be a stratum with
![]() $a_i>0$
for all i. The following holds:
$a_i>0$
for all i. The following holds:
-
•
 ${{\mathcal {H}}}$
has three connected components in the following cases:
${{\mathcal {H}}}$
has three connected components in the following cases:-
–
 $k=1, a_1 = 2g-2, g \geq 4.$
$k=1, a_1 = 2g-2, g \geq 4.$
-
–
 $k=2$
,
$k=2$
,
 $a_1 = a_2 = g-1$
,
$a_1 = a_2 = g-1$
,
 $g \geq 5$
is odd. One is hyperelliptic, and the two non-hyperelliptic strata are distinguished by the spin invariant.
$g \geq 5$
is odd. One is hyperelliptic, and the two non-hyperelliptic strata are distinguished by the spin invariant.
-
-
•
 ${{\mathcal {H}}}$
has two connected components in the following cases:
${{\mathcal {H}}}$
has two connected components in the following cases:-
– All of the
 $a_i$
are even,
$a_i$
are even,
 $g \geq 4$
, and either
$g \geq 4$
, and either
 $k \geq 3$
or
$k \geq 3$
or
 $a_1> a_2$
. The components are distinguished by their spin.
$a_1> a_2$
. The components are distinguished by their spin. -
–
 $a_1 = a_2$
and g is either
$a_1 = a_2$
and g is either
 $3$
or is even. One of the components is hyperelliptic and the other is not. When
$3$
or is even. One of the components is hyperelliptic and the other is not. When
 $g=3$
, the hyperelliptic component is even, and the other one is odd.
$g=3$
, the hyperelliptic component is even, and the other one is odd.
-
-
•
 ${{\mathcal {H}}}$
is connected in all other cases.
${{\mathcal {H}}}$
is connected in all other cases.
Proof of Proposition 8.2.
The proof will be case-by-case. Here are the cases:
-
(i)
 ${{\mathcal {H}}}(1,1)$
.
${{\mathcal {H}}}(1,1)$
. -
(ii) All the
 $a_i$
are nonzero, and
$a_i$
are nonzero, and
 ${{\mathcal {H}}}$
is connected.
${{\mathcal {H}}}$
is connected. -
(iii) All the
 $a_i$
are nonzero, and
$a_i$
are nonzero, and
 ${{\mathcal {H}}}$
has two connected components distinguished by spin.
${{\mathcal {H}}}$
has two connected components distinguished by spin. -
(iv) All the
 $a_i$
are nonzero, and
$a_i$
are nonzero, and
 ${{\mathcal {H}}}$
has two connected components distinguished by hyperellipticity.
${{\mathcal {H}}}$
has two connected components distinguished by hyperellipticity. -
(v) All the
 $a_i$
are nonzero, and
$a_i$
are nonzero, and
 ${{\mathcal {H}}}$
has three connected components.
${{\mathcal {H}}}$
has three connected components. -
(vi) Some of the
 $a_i$
are zero.
$a_i$
are zero.
Case (i). There is just one connected component, and the desired surface is a Z-shaped surface, with three horizontal cylinders
![]() $C_1, C_2, C_3$
of circumferences
$C_1, C_2, C_3$
of circumferences
![]() $c_1, c_1+c_3, c_3$
, where
$c_1, c_1+c_3, c_3$
, where
![]() $C_1, C_3$
are simple. We put all of the removable singular points in the interior of
$C_1, C_3$
are simple. We put all of the removable singular points in the interior of
![]() $C_3$
and choose
$C_3$
and choose
![]() $c_1, c_3$
so that
$c_1, c_3$
so that
![]() $c_1/(c_1+c_3) \notin {\mathbb {Q}}$
. It is clear that with these choices, the conditions are satisfied.
$c_1/(c_1+c_3) \notin {\mathbb {Q}}$
. It is clear that with these choices, the conditions are satisfied.
Case (ii). The stratum
![]() ${{\mathcal {H}}}$
is connected, and we have at least two singularities of positive order. So with no loss of generality, they are labelled 1 and 2. The result follows from Lemma 8.4, applied to a surface in
${{\mathcal {H}}}$
is connected, and we have at least two singularities of positive order. So with no loss of generality, they are labelled 1 and 2. The result follows from Lemma 8.4, applied to a surface in
![]() ${{\mathcal {H}}}(a_1-1, a_2-1, a_3, \ldots , a_k)$
and taking
${{\mathcal {H}}}(a_1-1, a_2-1, a_3, \ldots , a_k)$
and taking
![]() $w\notin c\mathbb {Q}$
, so that
$w\notin c\mathbb {Q}$
, so that
![]() $w/(c+w) \notin {\mathbb {Q}}$
.
$w/(c+w) \notin {\mathbb {Q}}$
.
Case (iii). We apply the surgery in Lemma 8.5, with
![]() $w_1/w_2 \notin {\mathbb {Q}}$
. Namely, if p and q are labelled
$w_1/w_2 \notin {\mathbb {Q}}$
. Namely, if p and q are labelled
![]() $i, j$
, we let
$i, j$
, we let
![]() $b_i = a_i-2$
,
$b_i = a_i-2$
,
![]() $b_j = a_j-2$
and
$b_j = a_j-2$
and
![]() $b_\ell = a_\ell $
for
$b_\ell = a_\ell $
for
![]() $\ell \neq i,j$
.
$\ell \neq i,j$
.
Case (iv). There are two connected components. One is hyperelliptic; one is not. This means that
![]() $a_1 = a_2$
and either
$a_1 = a_2$
and either
![]() $g=3$
(in which case
$g=3$
(in which case
![]() $a_1 = a_2 = 2$
) or
$a_1 = a_2 = 2$
) or
![]() $g \geq 4$
is even (in which case
$g \geq 4$
is even (in which case
![]() $a_1 = a_2 = g-1$
). In this case, we give explicit surfaces, one in each connected component. The first surface (the
$a_1 = a_2 = g-1$
). In this case, we give explicit surfaces, one in each connected component. The first surface (the
![]() ${{\mathcal {H}}}(2,2)$
case is shown in Figure 7) is a ‘staircase’ surface made of gluing
${{\mathcal {H}}}(2,2)$
case is shown in Figure 7) is a ‘staircase’ surface made of gluing
![]() $2g$
rectangles to each other. The rectangles are labelled
$2g$
rectangles to each other. The rectangles are labelled
![]() $(k, B)$
and
$(k, B)$
and
![]() $(k, T)$
for
$(k, T)$
for
![]() $k = 1 , \ldots , g$
. The top (respectively, bottom) of
$k = 1 , \ldots , g$
. The top (respectively, bottom) of
![]() $(k, B)$
is glued to the bottom (resp., top) of
$(k, B)$
is glued to the bottom (resp., top) of
![]() $(k,T)$
for
$(k,T)$
for
![]() $k=1, \ldots , g$
, and the left (resp., right) of
$k=1, \ldots , g$
, and the left (resp., right) of
![]() $(k, T)$
is glued to the right (resp., left) of
$(k, T)$
is glued to the right (resp., left) of
![]() $(k+1, B)$
for
$(k+1, B)$
for
![]() $k=1, \ldots , g-1$
. The horizontal sides of
$k=1, \ldots , g-1$
. The horizontal sides of
![]() $(1, B)$
are glued to each other, as are the horizontal sides of
$(1, B)$
are glued to each other, as are the horizontal sides of
![]() $(g, T)$
. This surface is hyperelliptic since it has a hyperelliptic involution rotating each rectangle around its midpoint, and this involution swaps the singularities (see [Reference Kontsevich and ZorichKZ, Remark 3]). The second surface is obtained as follows. We first construct a hyperelliptic surface in
$(g, T)$
. This surface is hyperelliptic since it has a hyperelliptic involution rotating each rectangle around its midpoint, and this involution swaps the singularities (see [Reference Kontsevich and ZorichKZ, Remark 3]). The second surface is obtained as follows. We first construct a hyperelliptic surface in
![]() ${{\mathcal {H}}}(a_1-2, a_2-2)$
as in the previous paragraph. Then we perform the surgery described in Lemma 8.5. The resulting surface has a horizontal cylinder intersecting three vertical cylinders and thus, by [Reference LindseyLi, Lemma 2.1], is not hyperelliptic. See Figure 8 for an example in
${{\mathcal {H}}}(a_1-2, a_2-2)$
as in the previous paragraph. Then we perform the surgery described in Lemma 8.5. The resulting surface has a horizontal cylinder intersecting three vertical cylinders and thus, by [Reference LindseyLi, Lemma 2.1], is not hyperelliptic. See Figure 8 for an example in
![]() ${{\mathcal {H}}}(2,2)$
. In both of these constructions, there are no restrictions on the sidelengths of the rectangles, and we can easily arrange that two of the circumferences are incommensurable.
${{\mathcal {H}}}(2,2)$
. In both of these constructions, there are no restrictions on the sidelengths of the rectangles, and we can easily arrange that two of the circumferences are incommensurable.

Figure 7 A surface in
![]() ${\mathcal {H}}^{hyp}(2,2)$
.
${\mathcal {H}}^{hyp}(2,2)$
.

Figure 8 A surface in
![]() ${\mathcal {H}}^{nonhyp}(2,2)$
.
${\mathcal {H}}^{nonhyp}(2,2)$
.
Case (v). In this case,
![]() $a_1 = a_2 = g-1$
for
$a_1 = a_2 = g-1$
for
![]() $g \geq 5$
odd. Applying the argument in Case (iii), we obtain the required surfaces in the odd and even connected components. To obtain the required surface in the hyperelliptic component, we use the ‘staircase surface’ described in Case (iv).
$g \geq 5$
odd. Applying the argument in Case (iii), we obtain the required surfaces in the odd and even connected components. To obtain the required surface in the hyperelliptic component, we use the ‘staircase surface’ described in Case (iv).
Case (vi). Assume with no loss of generality that the removable singularities are labelled
![]() $k'+1, \ldots , k$
for some
$k'+1, \ldots , k$
for some
![]() $k' \geq 2$
, and let
$k' \geq 2$
, and let
![]() ${{\mathcal {H}}}' = {{\mathcal {H}}}(a_1, \ldots , a_{k'})$
. Note that the singularities p and q have label in
${{\mathcal {H}}}' = {{\mathcal {H}}}(a_1, \ldots , a_{k'})$
. Note that the singularities p and q have label in
![]() $\{1, \ldots , k'\}$
. Apply the preceding considerations to obtain a surface in
$\{1, \ldots , k'\}$
. Apply the preceding considerations to obtain a surface in
![]() ${{\mathcal {H}}}'$
with the required cylinders. By examining the proof in all preceding cases, one sees that the number of horizontal cylinders on this surface is at least three; that is, there is at least one cylinder
${{\mathcal {H}}}'$
with the required cylinders. By examining the proof in all preceding cases, one sees that the number of horizontal cylinders on this surface is at least three; that is, there is at least one cylinder
![]() $C_3$
which is distinct from the cylinders
$C_3$
which is distinct from the cylinders
![]() $C_1, C_2$
, and we modify M by adding
$C_1, C_2$
, and we modify M by adding
![]() $k-k'$
points in general position in the interior of
$k-k'$
points in general position in the interior of
![]() $C_3$
, to obtain the desired surface.
$C_3$
, to obtain the desired surface.
9. Zero entropy
In this section, we prove the following result:
Theorem 9.1. Let
![]() ${\mathcal {H}}$
be a stratum for which
${\mathcal {H}}$
be a stratum for which
![]() $\dim Z>0$
, let
$\dim Z>0$
, let
![]() $z \in Z \smallsetminus \{0\}$
, and let
$z \in Z \smallsetminus \{0\}$
, and let
![]() $\mu $
be a probability measure on
$\mu $
be a probability measure on
![]() ${\mathcal {H}}$
such that
${\mathcal {H}}$
such that
![]() $\mathrm {Rel}_{z} (q)$
is defined for
$\mathrm {Rel}_{z} (q)$
is defined for
![]() $\mu $
-a.e. q. Assume that
$\mu $
-a.e. q. Assume that
![]() $\mu $
is
$\mu $
is
![]() $\mathrm {Rel}_{z}$
-invariant and ergodic, and assume in addition that
$\mathrm {Rel}_{z}$
-invariant and ergodic, and assume in addition that
(in the weak-* topology). Then the entropy of
![]() $\mathrm {Rel}_z$
acting on
$\mathrm {Rel}_z$
acting on
![]() $({\mathcal {H}}, \mu )$
is zero.
$({\mathcal {H}}, \mu )$
is zero.
For the proof of Theorem 9.1, we will need an estimate showing that points stay close to each other for times up to L, provided their initial distance is polynomially small (as a function of L). To make this precise, we will use the sup-norm Finsler metric on
![]() ${\mathcal {H}}$
, which was introduced by Avila, Gouëzel and Yoccoz [Reference Avila, Gouëzel and YoccozAGY] and whose definition we now recall. For
${\mathcal {H}}$
, which was introduced by Avila, Gouëzel and Yoccoz [Reference Avila, Gouëzel and YoccozAGY] and whose definition we now recall. For
![]() $q_0, q_1$
belonging to the same connected component of a stratum
$q_0, q_1$
belonging to the same connected component of a stratum
![]() ${\mathcal {H}}$
, we write
${\mathcal {H}}$
, we write
 $$ \begin{align}\mathrm{dist}(q_0, q_1) = \inf_\gamma \int_0^1 \|\gamma'(t)\|_{\gamma(t)} dt, \end{align} $$
$$ \begin{align}\mathrm{dist}(q_0, q_1) = \inf_\gamma \int_0^1 \|\gamma'(t)\|_{\gamma(t)} dt, \end{align} $$
where
![]() $\gamma : [0,1]\to {\mathcal {H}}_{\mathrm {m}}$
ranges over all
$\gamma : [0,1]\to {\mathcal {H}}_{\mathrm {m}}$
ranges over all
![]() $C^1$
curves with
$C^1$
curves with
![]() $\gamma (0) \in \pi ^{-1}(q_0), \ \gamma (1) \in \pi ^{-1}(q_1)$
, and
$\gamma (0) \in \pi ^{-1}(q_0), \ \gamma (1) \in \pi ^{-1}(q_1)$
, and
![]() $\|\cdot \|_{\mathbf {q}}$
is a pointwise norm on the tangent space to
$\|\cdot \|_{\mathbf {q}}$
is a pointwise norm on the tangent space to
![]() ${\mathcal {H}}_{\mathrm {m}}$
at
${\mathcal {H}}_{\mathrm {m}}$
at
![]() $\mathbf {q}$
, identified via the developing map with
$\mathbf {q}$
, identified via the developing map with
![]() $H^1(S, \Sigma; {\mathbb {R}}^2)$
. Below, balls, diameters of sets and
$H^1(S, \Sigma; {\mathbb {R}}^2)$
. Below, balls, diameters of sets and
![]() $\varepsilon $
-neighborhoods of sets will be defined using this metric. We can now state our estimate.
$\varepsilon $
-neighborhoods of sets will be defined using this metric. We can now state our estimate.
Proposition 9.2. Let
![]() ${\mathcal {H}}$
be a stratum of translation surfaces with at least two singularities, let Z be its real Rel space, let
${\mathcal {H}}$
be a stratum of translation surfaces with at least two singularities, let Z be its real Rel space, let
![]() $z_0 \in Z$
, and let T be the map of
$z_0 \in Z$
, and let T be the map of
![]() ${\mathcal {H}}$
defined by applying
${\mathcal {H}}$
defined by applying
![]() $\mathrm {Rel}_{z_0}$
(where defined). Then for every compact subset
$\mathrm {Rel}_{z_0}$
(where defined). Then for every compact subset
![]() $K \subset {\mathcal {H}}$
, there is
$K \subset {\mathcal {H}}$
, there is
![]() $L_0>0 $
, such that if
$L_0>0 $
, such that if
![]() $q \in {\mathcal {H}}, \ L \in {\mathbb {N}}, \ L>L_0 $
satisfy
$q \in {\mathcal {H}}, \ L \in {\mathbb {N}}, \ L>L_0 $
satisfy
then the maps
![]() $T, \ldots , T^L$
are all defined on
$T, \ldots , T^L$
are all defined on
![]() $B\left (q, \frac {1}{L^{5}} \right )$
, and we have
$B\left (q, \frac {1}{L^{5}} \right )$
, and we have
 $$ \begin{align*}\max_{j=1, \ldots, L} \mathrm{diam} \left( T^j \left(B \left(q, \frac{1 }{L^{5}} \right) \right) \right) \to_{L \to \infty} 0. \end{align*} $$
$$ \begin{align*}\max_{j=1, \ldots, L} \mathrm{diam} \left( T^j \left(B \left(q, \frac{1 }{L^{5}} \right) \right) \right) \to_{L \to \infty} 0. \end{align*} $$
We have made no attempt to optimize the power 5 in this statement.
Our proof of Proposition 9.2 will use some properties of the sup-norm metric. They are proved in [Reference Avila, Gouëzel and YoccozAGY]; see also [Reference Avila and GouëzelAG] and [Reference Chaika, Smillie and WeissCSW, §2]. Our notation will follow the one used in [Reference Chaika, Smillie and WeissCSW].
Proposition 9.3. The following hold:
-
(a) For all
 $q_0, q_1$
and all
$q_0, q_1$
and all
 $t \in {\mathbb {R}}$
,
$t \in {\mathbb {R}}$
,
 $ \mathrm {dist}(g_t q_0, g_t q_1) \leq e^{2|t|} \mathrm {dist}(q_0, q_1). $
$ \mathrm {dist}(g_t q_0, g_t q_1) \leq e^{2|t|} \mathrm {dist}(q_0, q_1). $
-
(b) The metric dist is proper; that is, for any fixed basepoint
 $q_0$
, the map
$q_0$
, the map
 $q \mapsto \mathrm {dist}(q, q_0)$
is proper. In particular, the
$q \mapsto \mathrm {dist}(q, q_0)$
is proper. In particular, the
 $\varepsilon $
-neighborhood of a compact set is pre-compact, for any
$\varepsilon $
-neighborhood of a compact set is pre-compact, for any
 $\varepsilon>0$
.
$\varepsilon>0$
. -
(c) The map
 ${\mathbf {q}} \mapsto \| \cdot \|_{\mathbf {q}}$
is continuous and hence bounded on compact sets. This means that for any compact
${\mathbf {q}} \mapsto \| \cdot \|_{\mathbf {q}}$
is continuous and hence bounded on compact sets. This means that for any compact
 $K \subset {\mathcal {H}}_{\mathrm {m}}$
, there is
$K \subset {\mathcal {H}}_{\mathrm {m}}$
, there is
 $C>0$
such that for any
$C>0$
such that for any
 ${\mathbf {q}}_0, {\mathbf {q}}_1$
in K, the norms
${\mathbf {q}}_0, {\mathbf {q}}_1$
in K, the norms
 $\| \cdot \|_{{\mathbf {q}}_0} , \, \| \cdot \|_{{\mathbf {q}}_1}$
are bi-Lipschitz equivalent with constant C.
$\| \cdot \|_{{\mathbf {q}}_0} , \, \| \cdot \|_{{\mathbf {q}}_1}$
are bi-Lipschitz equivalent with constant C. -
(d) The infimum in (9.2) is actually a minimum that is attained by some curve
 $\gamma $
.
$\gamma $
.
With these preparations, we can give the following:
Proof of Proposition 9.2.
Write
![]() $B {\, \stackrel {\mathrm {def}}{=}\, } B\left (q, \frac {1}{L^{5}} \right ), \, A {\, \stackrel {\mathrm {def}}{=}\, } g_{-\ell }(B)$
(note that A and B both depend on L and q, but we suppress this from the notation). Let
$B {\, \stackrel {\mathrm {def}}{=}\, } B\left (q, \frac {1}{L^{5}} \right ), \, A {\, \stackrel {\mathrm {def}}{=}\, } g_{-\ell }(B)$
(note that A and B both depend on L and q, but we suppress this from the notation). Let
![]() $K'$
be the 1-neighborhood of K, which is a pre-compact subset of
$K'$
be the 1-neighborhood of K, which is a pre-compact subset of
![]() ${\mathcal {H}}$
by Proposition 9.3(b). Since
${\mathcal {H}}$
by Proposition 9.3(b). Since
![]() $\mathrm {diam}(B) \leq \frac {2}{L^{5}}$
, Proposition 9.3(a) implies that
$\mathrm {diam}(B) \leq \frac {2}{L^{5}}$
, Proposition 9.3(a) implies that
It follows from (9.3) that
![]() $A \cap K \neq \varnothing $
, and therefore,
$A \cap K \neq \varnothing $
, and therefore,
![]() $A \subset K'$
. Since
$A \subset K'$
. Since
for all large enough L (depending on
![]() $K'$
), we have that
$K'$
), we have that
![]() $\mathrm {Rel}_{je^{-\ell }z_0}(q')$
is defined for
$\mathrm {Rel}_{je^{-\ell }z_0}(q')$
is defined for
![]() $q' \in K'$
. Since
$q' \in K'$
. Since
![]() $q^{\prime }_1 {\, \stackrel {\mathrm {def}}{=}\, } \mathrm {Rel}_{je^{-\ell }z_0}\circ g_{-\ell }(q_1)$
is defined for
$q^{\prime }_1 {\, \stackrel {\mathrm {def}}{=}\, } \mathrm {Rel}_{je^{-\ell }z_0}\circ g_{-\ell }(q_1)$
is defined for
![]() $q_1 \in B$
, we have from (2.3) that
$q_1 \in B$
, we have from (2.3) that
![]() $T^j(q_1) =\mathrm {Rel}_{jz_0}(q_1) = g_{\ell }(q^{\prime }_1) $
is also defined. This proves that the maps
$T^j(q_1) =\mathrm {Rel}_{jz_0}(q_1) = g_{\ell }(q^{\prime }_1) $
is also defined. This proves that the maps
![]() $T, T^2, \ldots , T^L$
are all defined on B.
$T, T^2, \ldots , T^L$
are all defined on B.
Furthermore, this computation shows that
![]() $T^j(B) = g_\ell (\mathrm {Rel}_{je^{-\ell }z_0} (A))$
, and so by Proposition 9.3(a), it suffices to show that
$T^j(B) = g_\ell (\mathrm {Rel}_{je^{-\ell }z_0} (A))$
, and so by Proposition 9.3(a), it suffices to show that
Taking into account (9.4) and (9.5), it suffices to show that for any compact
![]() $K'$
, there are positive
$K'$
, there are positive
![]() $\varepsilon , C$
such that for any
$\varepsilon , C$
such that for any
![]() $q_0, q_1 \in K'$
with
$q_0, q_1 \in K'$
with
![]() $\mathrm {dist}(q_0, q_1) < \varepsilon $
, and any
$\mathrm {dist}(q_0, q_1) < \varepsilon $
, and any
![]() $z \in Z$
with
$z \in Z$
with
![]() $\|z\|< \varepsilon $
, we have
$\|z\|< \varepsilon $
, we have
Informally, this is a uniform local Lipschitz estimate for the family of maps defined by small elements of Z.
To see (9.6), let
![]() $\varepsilon _1$
be small enough so that for any
$\varepsilon _1$
be small enough so that for any
![]() $q \in K'$
, the ball
$q \in K'$
, the ball
![]() $B(q, 2\varepsilon _1)$
is contained in a neighborhood which is evenly covered by the map
$B(q, 2\varepsilon _1)$
is contained in a neighborhood which is evenly covered by the map
![]() $\pi : {\mathcal {H}}_{\mathrm {m}} \to {\mathcal {H}}$
, and let C be a bound as in Proposition 9.3(c), corresponding to the compact set which is the
$\pi : {\mathcal {H}}_{\mathrm {m}} \to {\mathcal {H}}$
, and let C be a bound as in Proposition 9.3(c), corresponding to the compact set which is the
![]() $2\varepsilon _1$
-neighborhood of
$2\varepsilon _1$
-neighborhood of
![]() $K'$
. Let
$K'$
. Let
![]() $\varepsilon < \varepsilon _1$
so that for any
$\varepsilon < \varepsilon _1$
so that for any
![]() $z \in Z$
with
$z \in Z$
with
![]() $\|z\|< \varepsilon $
and any
$\|z\|< \varepsilon $
and any
![]() $q \in {\mathcal {H}}$
,
$q \in {\mathcal {H}}$
,
![]() $\mathrm {dist}(q, \mathrm {Rel}_{z}(q))< \varepsilon _1$
. If
$\mathrm {dist}(q, \mathrm {Rel}_{z}(q))< \varepsilon _1$
. If
![]() $\mathrm {dist}(q_0, q_1)<\varepsilon $
, then the path
$\mathrm {dist}(q_0, q_1)<\varepsilon $
, then the path
![]() $\gamma $
realizing their distance (see Proposition 9.3(d)) is contained in a connected component
$\gamma $
realizing their distance (see Proposition 9.3(d)) is contained in a connected component
![]() $\mathcal {V}$
of
$\mathcal {V}$
of
![]() $\pi ^{-1}\left (B(q_0, \varepsilon _1) \right )$
. Let
$\pi ^{-1}\left (B(q_0, \varepsilon _1) \right )$
. Let
let
and analogously define
By choice of
![]() $\varepsilon $
and
$\varepsilon $
and
![]() $\varepsilon _1$
, the curve
$\varepsilon _1$
, the curve
![]() $\gamma _1$
also has its image in
$\gamma _1$
also has its image in
![]() $\mathcal {V}$
. Since
$\mathcal {V}$
. Since
![]() $\mathrm {Rel}_{z}$
is expressed by
$\mathrm {Rel}_{z}$
is expressed by
![]() $\mathrm {dev}|_{\mathcal {V}}$
as a translation map, the curves
$\mathrm {dev}|_{\mathcal {V}}$
as a translation map, the curves
![]() $\bar \gamma , \bar \gamma _1$
are identical maps. When computing
$\bar \gamma , \bar \gamma _1$
are identical maps. When computing
![]() $\mathrm {dist}(\mathrm {Rel}_{z}(q_0), \mathrm {Rel}_{z}(q_1))$
via (9.2), an upper bound is given by computing the path integral along the curve
$\mathrm {dist}(\mathrm {Rel}_{z}(q_0), \mathrm {Rel}_{z}(q_1))$
via (9.2), an upper bound is given by computing the path integral along the curve
![]() $\gamma _1$
. We compare this path integral along
$\gamma _1$
. We compare this path integral along
![]() $\gamma _1$
, with the path integral along
$\gamma _1$
, with the path integral along
![]() $\gamma $
giving
$\gamma $
giving
![]() $\mathrm {dist}(q_0, q_1)$
. In these two integrals, for any t, the tangent vectors
$\mathrm {dist}(q_0, q_1)$
. In these two integrals, for any t, the tangent vectors
![]() $\gamma '(t), \gamma ^{\prime }_1(t)$
are identical elements of
$\gamma '(t), \gamma ^{\prime }_1(t)$
are identical elements of
![]() $H^1(S, \Sigma; {\mathbb {R}}^2))$
for all t, but the norms are evaluated using different basepoints. Since these basepoints are all in the
$H^1(S, \Sigma; {\mathbb {R}}^2))$
for all t, but the norms are evaluated using different basepoints. Since these basepoints are all in the
![]() $2\varepsilon _1$
-neighborhood of
$2\varepsilon _1$
-neighborhood of
![]() $K'$
, by choice of C, we have
$K'$
, by choice of C, we have
![]() $\|\gamma _1'(t)\|_{\gamma _1(t)} \leq C \|\gamma '(t) \|_{\gamma (t)}$
for all t. This implies (9.6).
$\|\gamma _1'(t)\|_{\gamma _1(t)} \leq C \|\gamma '(t) \|_{\gamma (t)}$
for all t. This implies (9.6).
We now list a few additional results we will need. The first is the following weak Besicovitch-type covering Lemma for balls of equal size.
Proposition 9.4. For any compact
![]() $K \subset {\mathcal {H}}$
, there is
$K \subset {\mathcal {H}}$
, there is
![]() $N \in {\mathbb {N}}$
so that for any
$N \in {\mathbb {N}}$
so that for any
![]() $r \in (0, 1)$
, for any
$r \in (0, 1)$
, for any
![]() $G \subset K$
, the collection
$G \subset K$
, the collection
![]() $\mathcal {C} {\, \stackrel {\mathrm {def}}{=}\, } \{B(q, r): q \in G\}$
contains N finite subcollections
$\mathcal {C} {\, \stackrel {\mathrm {def}}{=}\, } \{B(q, r): q \in G\}$
contains N finite subcollections
![]() $\mathcal {F}_1, \ldots , \mathcal {F}_N$
satisfying
$\mathcal {F}_1, \ldots , \mathcal {F}_N$
satisfying
![]() $G \subset \bigcup _{i=1}^N \bigcup \mathcal {F}_i, $
and each collection
$G \subset \bigcup _{i=1}^N \bigcup \mathcal {F}_i, $
and each collection
![]() $\mathcal {F}_i$
consists of disjoint balls.
$\mathcal {F}_i$
consists of disjoint balls.
Proof. The argument is standard; we sketch it for lack of a suitable reference.
We first claim that given a compact K, there is N so that for any
![]() $r \in (0, 1)$
, the largest r-separated subset of any ball of radius
$r \in (0, 1)$
, the largest r-separated subset of any ball of radius
![]() $2r$
has cardinality at most N. Indeed, this property is true for Euclidean space (for any r) by a simple volume argument and is invariant under biLipschitz maps (up to changing the constant N). For any compact K, let
$2r$
has cardinality at most N. Indeed, this property is true for Euclidean space (for any r) by a simple volume argument and is invariant under biLipschitz maps (up to changing the constant N). For any compact K, let
![]() $K_1$
be the
$K_1$
be the
![]() $1$
-neighborhood of K in
$1$
-neighborhood of K in
![]() ${\mathcal {H}}$
, which is also compact by Proposition 9.3(b) and contains all balls in
${\mathcal {H}}$
, which is also compact by Proposition 9.3(b) and contains all balls in
![]() ${\mathcal {H}}$
which are centered in K and have radius
${\mathcal {H}}$
which are centered in K and have radius
![]() $r < 1$
. Now the claim holds by Proposition 9.3(c).
$r < 1$
. Now the claim holds by Proposition 9.3(c).
We now inductively choose the
![]() $\mathcal {F}_i$
. Let
$\mathcal {F}_i$
. Let
![]() $\mathcal {F}_1$
be a maximal collection of disjoint balls of radius r with centers in G. For
$\mathcal {F}_1$
be a maximal collection of disjoint balls of radius r with centers in G. For
![]() $i \geq 2$
, suppose
$i \geq 2$
, suppose
![]() $\mathcal {F}_1, \ldots , \mathcal {F}_{i-1}$
have been chosen, let
$\mathcal {F}_1, \ldots , \mathcal {F}_{i-1}$
have been chosen, let
![]() $G_i {\, \stackrel {\mathrm {def}}{=}\, } G \smallsetminus \bigcup _{j=1}^{i-1} \bigcup \mathcal {F}_j$
, and let
$G_i {\, \stackrel {\mathrm {def}}{=}\, } G \smallsetminus \bigcup _{j=1}^{i-1} \bigcup \mathcal {F}_j$
, and let
![]() $\mathcal {F}_i$
be the maximal collection of disjoint balls of radius r with centers in
$\mathcal {F}_i$
be the maximal collection of disjoint balls of radius r with centers in
![]() $G_i$
. Clearly,
$G_i$
. Clearly,
![]() $G \supset G_1 \supset \cdots \supset G_N$
, and we need to show that
$G \supset G_1 \supset \cdots \supset G_N$
, and we need to show that
![]() $G_{N+1} = \varnothing $
. Since
$G_{N+1} = \varnothing $
. Since
![]() $\mathcal {F}_i$
is maximal, for any
$\mathcal {F}_i$
is maximal, for any
![]() $x \in G_i$
there is
$x \in G_i$
there is
![]() $x'$
which is the center of one of the balls of
$x'$
which is the center of one of the balls of
![]() $\mathcal {F}_i$
, so that
$\mathcal {F}_i$
, so that
![]() $d(x,x') < 2r$
. If
$d(x,x') < 2r$
. If
![]() $x \in G_{N+1} \neq \varnothing $
, then the ball
$x \in G_{N+1} \neq \varnothing $
, then the ball
![]() $B(x, 2r)$
contains
$B(x, 2r)$
contains
![]() $x_1, \ldots , x_N$
such that
$x_1, \ldots , x_N$
such that
![]() $x_i$
is the center of one of the balls of
$x_i$
is the center of one of the balls of
![]() $\mathcal {F}_i$
. For
$\mathcal {F}_i$
. For
![]() $i'>i$
,
$i'>i$
,
![]() $d(x_i, x_{i'}) \geq r$
since
$d(x_i, x_{i'}) \geq r$
since
![]() $x_{i'} \in G_{i'}$
. This contradicts the property of N from the preceding paragraph.
$x_{i'} \in G_{i'}$
. This contradicts the property of N from the preceding paragraph.
We will need to know that volumes of balls do not decay exponentially:
Lemma 9.5. For any probability measure
![]() $\mu $
on
$\mu $
on
![]() ${\mathcal {H}}$
, for any n, for
${\mathcal {H}}$
, for any n, for
![]() $\mu $
-a.e. x, we have
$\mu $
-a.e. x, we have
Proof. Sketch of proof.
We fix n. Observe that (9.7) says that for almost every point x, for all
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
![]() $e^{-\varepsilon r^{-\frac 1 n}}$
is
$e^{-\varepsilon r^{-\frac 1 n}}$
is
![]() $o(\mu (B(x,r)))$
, as
$o(\mu (B(x,r)))$
, as
![]() $r \to 0$
. Let K be a compact subset of
$r \to 0$
. Let K be a compact subset of
![]() ${\mathcal {H}}$
, and let
${\mathcal {H}}$
, and let
![]() $d = \dim {\mathcal {H}}$
. For all small enough r, we can cover K by
$d = \dim {\mathcal {H}}$
. For all small enough r, we can cover K by
![]() $O\left (r^{-d} \right )$
balls of radius r; we let
$O\left (r^{-d} \right )$
balls of radius r; we let
![]() $\mathcal {B}_r=\{B(x_i,r)\}$
denote such a finite collection of balls. If
$\mathcal {B}_r=\{B(x_i,r)\}$
denote such a finite collection of balls. If
![]() $B = B(x,r) $
, then any element of
$B = B(x,r) $
, then any element of
![]() $\mathcal {B}_{\frac {r}3}$
that contains x is contained in B and hence has measure at most
$\mathcal {B}_{\frac {r}3}$
that contains x is contained in B and hence has measure at most
![]() $\mu (B)$
. For
$\mu (B)$
. For
![]() $k \in {\mathbb {N}}$
, let
$k \in {\mathbb {N}}$
, let
so that
 $$ \begin{align} \mu\left(\bigcup_{B \in \mathcal{E}_k} B\right) = O\left( 2^{kd} e^{-2^{k/(2n)}}\right). \end{align} $$
$$ \begin{align} \mu\left(\bigcup_{B \in \mathcal{E}_k} B\right) = O\left( 2^{kd} e^{-2^{k/(2n)}}\right). \end{align} $$
Since K was arbitrary, it suffices to show that a.e.
![]() $x \in K$
belongs to at most finitely many of the sets
$x \in K$
belongs to at most finitely many of the sets
![]() $\mathcal {E}_k$
; this follows from (9.8) and Borel-Cantelli.
$\mathcal {E}_k$
; this follows from (9.8) and Borel-Cantelli.
We also need some standard facts about entropy. In the following proposition, X is a standard Borel space,
![]() $T: X \to X$
is a measurable map,
$T: X \to X$
is a measurable map,
![]() ${\mathrm {Prob}}(X)^T$
denotes the T-invariant Borel probability measures on X,
${\mathrm {Prob}}(X)^T$
denotes the T-invariant Borel probability measures on X,
![]() $\mu $
is a measure in
$\mu $
is a measure in
![]() ${\mathrm {Prob}}(X)^T$
,
${\mathrm {Prob}}(X)^T$
,
![]() $\mathcal {P}$
is a measurable partition of X, and
$\mathcal {P}$
is a measurable partition of X, and
![]() $h_\mu (T, \mathcal {P})$
is the entropy of T with respect to
$h_\mu (T, \mathcal {P})$
is the entropy of T with respect to
![]() $\mu $
and
$\mu $
and
![]() $\mathcal {P}$
. Then the entropy of T with respect to
$\mathcal {P}$
. Then the entropy of T with respect to
![]() $\mu $
is
$\mu $
is
![]() $\sup _{\mathcal {P}} h_\mu (T, \mathcal {P})$
, where the supremum ranges over all finite
$\sup _{\mathcal {P}} h_\mu (T, \mathcal {P})$
, where the supremum ranges over all finite
![]() $\mathcal {P}$
. For
$\mathcal {P}$
. For
![]() $x \in X$
,
$x \in X$
,
![]() $\mathcal {P}_n(x)$
is the atom of the finite refinement
$\mathcal {P}_n(x)$
is the atom of the finite refinement
![]() $\bigvee _{i=0}^n T^{-i}\mathcal {P}$
containing x.
$\bigvee _{i=0}^n T^{-i}\mathcal {P}$
containing x.
Proposition 9.6. We have the following:
-
(1) [Shannon-McMillan-Breiman Theorem.] If
 $\mu $
is ergodic, then for
$\mu $
is ergodic, then for
 $\mu $
-a.e. x, we have
$\mu $
-a.e. x, we have  $$ \begin{align*}\lim_{n \to \infty} \frac{-\log(\mu(\mathcal{P}_n(x)))}{n} = h_\mu(T, \mathcal{P}).\end{align*} $$
$$ \begin{align*}\lim_{n \to \infty} \frac{-\log(\mu(\mathcal{P}_n(x)))}{n} = h_\mu(T, \mathcal{P}).\end{align*} $$
-
(2) [Entropy and convex combinations.] If
 $\mu = \int _{{\mathrm {Prob}}(X)^T} \nu \ d\theta $
, for some probability measure
$\mu = \int _{{\mathrm {Prob}}(X)^T} \nu \ d\theta $
, for some probability measure
 $\theta $
on
$\theta $
on
 ${\mathrm {Prob}}(X)^T$
, then
${\mathrm {Prob}}(X)^T$
, then  $$ \begin{align*}h_{\mu}(T, \mathcal{P}) = \int_{{\mathrm{Prob}}(X)^T}h_\nu(T, \mathcal{P}) \ d\theta. \end{align*} $$
$$ \begin{align*}h_{\mu}(T, \mathcal{P}) = \int_{{\mathrm{Prob}}(X)^T}h_\nu(T, \mathcal{P}) \ d\theta. \end{align*} $$
-
(3) [Partitions with small boundary.] Let X be a locally compact, separable metrizable space. Then
 $h_\mu (T) = \sup _{\mathcal {P} \in \mathrm {Part}_0} h_\mu (T, \mathcal {P})$
, where
$h_\mu (T) = \sup _{\mathcal {P} \in \mathrm {Part}_0} h_\mu (T, \mathcal {P})$
, where
 $\mathrm {Part}_0$
denotes the finite partitions of X into sets
$\mathrm {Part}_0$
denotes the finite partitions of X into sets
 $P_i$
satisfy
$P_i$
satisfy
 $\mu (\partial P_i)=0$
for all i.
$\mu (\partial P_i)=0$
for all i.
For items (1) and (2), see, for example, [Reference GlasnerGl, Thms. 14.35 & 15.12] or [Reference Einsiedler, Lindenstrauss and WardELW, Chaps. 2 & 3]. Item (3) is left as an exercise (see [Reference Einsiedler, Lindenstrauss and WardELW, Pf. of Thm. 2.2]).
Proof of Theorem 9.1.
We assume that the entropy
![]() $h = h_\mu (T)$
satisfies
$h = h_\mu (T)$
satisfies
![]() $h>0$
, and we will derive a contradiction. Using Proposition 9.6(3), we choose a partition
$h>0$
, and we will derive a contradiction. Using Proposition 9.6(3), we choose a partition
![]() $\mathcal {P}=\{P_i\}_{i=1}^k$
so that
$\mathcal {P}=\{P_i\}_{i=1}^k$
so that
![]() $\mu (\partial P_i)=0$
for each i and
$\mu (\partial P_i)=0$
for each i and
![]() $h_\mu (T, \mathcal {P})> \frac {h}{2}$
. Choose K compact so that
$h_\mu (T, \mathcal {P})> \frac {h}{2}$
. Choose K compact so that
![]() $\mu (K)>\frac 3 4 $
and
$\mu (K)>\frac 3 4 $
and
A compact set with this property exists by the nondivergence assumption (9.1). Let N and
![]() $r_0$
be as in Proposition 9.4 for this choice of K. Using the Shannon-McMillan-Breiman theorem, let
$r_0$
be as in Proposition 9.4 for this choice of K. Using the Shannon-McMillan-Breiman theorem, let
![]() $L_0$
be large enough so that for all
$L_0$
be large enough so that for all
![]() $L> L_0$
, the set
$L> L_0$
, the set
 $$ \begin{align*}W {\, \stackrel{\mathrm{def}}{=}\, } \left\{q: \frac{-\log (\mu(P_L(q)))}{L} \leq \frac{h}{2} \right\} \end{align*} $$
$$ \begin{align*}W {\, \stackrel{\mathrm{def}}{=}\, } \left\{q: \frac{-\log (\mu(P_L(q)))}{L} \leq \frac{h}{2} \right\} \end{align*} $$
satisfies
Our goal will be to choose some
![]() $L>L_0$
for which we have a contradiction to (9.10).
$L>L_0$
for which we have a contradiction to (9.10).
Below, we will simplify notation by writing
![]() $ B\left (q, \frac {1}{L^{5}} \right )$
as
$ B\left (q, \frac {1}{L^{5}} \right )$
as
![]() $B_{q,L}$
or simply as B. Let
$B_{q,L}$
or simply as B. Let
 $$ \begin{align*}G_L {\, \stackrel{\mathrm{def}}{=}\, } \left\{ q : \mu \left( B_{q, L} \cap W \right)> \frac{\mu(B_{q, L})}{2} \right\}. \end{align*} $$
$$ \begin{align*}G_L {\, \stackrel{\mathrm{def}}{=}\, } \left\{ q : \mu \left( B_{q, L} \cap W \right)> \frac{\mu(B_{q, L})}{2} \right\}. \end{align*} $$
We will show below that
We first explain why (9.11) leads to a contradiction with (9.10). Let
![]() $L>L_0$
be large enough so that
$L>L_0$
be large enough so that
![]() $\mathrm {diam}(B) \leq \frac {2}{L^5} < r_0$
and
$\mathrm {diam}(B) \leq \frac {2}{L^5} < r_0$
and
![]() $\mu (K \cap G_L)> \frac {1}{3}$
, and let
$\mu (K \cap G_L)> \frac {1}{3}$
, and let
By Proposition 9.4, there is a subcollection
![]() $\mathcal {F} \subset \mathcal {C}$
, consisting of disjoint balls, so that
$\mathcal {F} \subset \mathcal {C}$
, consisting of disjoint balls, so that
Then we have
 $$ \begin{align*}\mu(W) \geq \mu\left(W \cap \bigcup \mathcal{F} \right) = \sum_{B \in \mathcal{F}} \mu(W \cap B)> \sum_{B \in \mathcal{F}} \frac{\mu(B)}{2} \geq \frac{\mu \left(\bigcup \mathcal{F} \right)}{2}\geq \frac{1}{6N}, \end{align*} $$
$$ \begin{align*}\mu(W) \geq \mu\left(W \cap \bigcup \mathcal{F} \right) = \sum_{B \in \mathcal{F}} \mu(W \cap B)> \sum_{B \in \mathcal{F}} \frac{\mu(B)}{2} \geq \frac{\mu \left(\bigcup \mathcal{F} \right)}{2}\geq \frac{1}{6N}, \end{align*} $$
where the equality follows from the disjointness of
![]() $\mathcal {F}$
and the strict inequality follows from the definitions of
$\mathcal {F}$
and the strict inequality follows from the definitions of
![]() $G_L$
and
$G_L$
and
![]() $\mathcal {C}.$
This gives the desired contradiction to (9.10).
$\mathcal {C}.$
This gives the desired contradiction to (9.10).
It remains to show (9.11). Choose
![]() $\varepsilon>0$
so that
$\varepsilon>0$
so that
Given any
![]() $L_1$
, let
$L_1$
, let
![]() $L>L_1$
, and let
$L>L_1$
, and let
![]() $X_0 = X_0(L) \subset K$
such that
$X_0 = X_0(L) \subset K$
such that
![]() $\mu (X_0) \geq \frac {1}{2},$
and so that for any
$\mu (X_0) \geq \frac {1}{2},$
and so that for any
![]() $q \in X_0$
, we have (9.3). Such L and
$q \in X_0$
, we have (9.3). Such L and
![]() $X_0$
exist by (9.9). Using Lemma 9.5 with
$X_0$
exist by (9.9). Using Lemma 9.5 with
![]() $n=5$
, we can take L large enough so that
$n=5$
, we can take L large enough so that
and by making L even larger, we can assume that
Now choose
![]() $r>0$
so that
$r>0$
so that
 $$ \begin{align} \mu(V ) < \varepsilon, \ \ \text{ where } \ V {\, \stackrel{\mathrm{def}}{=}\, } \left\{y: \mathrm{dist}\left(y,\bigcup_{i=1}^k \partial P_i\right)<r\right\} .\end{align} $$
$$ \begin{align} \mu(V ) < \varepsilon, \ \ \text{ where } \ V {\, \stackrel{\mathrm{def}}{=}\, } \left\{y: \mathrm{dist}\left(y,\bigcup_{i=1}^k \partial P_i\right)<r\right\} .\end{align} $$
This is possible because
![]() $\mu \left ( \bigcup _i \partial P_i \right )=0. $
$\mu \left ( \bigcup _i \partial P_i \right )=0. $
We claim that
To see this, define
and let
![]() $\mathbf {1}_V$
denote the indicator function of V. Using (9.15), and since
$\mathbf {1}_V$
denote the indicator function of V. Using (9.15), and since
![]() $\mu $
is T-invariant,
$\mu $
is T-invariant,
 $$ \begin{align*}\varepsilon L>L\mu(V)=\sum_{i=1}^L\int \mathbf{1}_V\left(T^iq\right) d\mu\geq 10 \varepsilon L \mu(E).\end{align*} $$
$$ \begin{align*}\varepsilon L>L\mu(V)=\sum_{i=1}^L\int \mathbf{1}_V\left(T^iq\right) d\mu\geq 10 \varepsilon L \mu(E).\end{align*} $$
Dividing through by
![]() $10L \varepsilon $
, we have
$10L \varepsilon $
, we have
![]() $\mu (E)<\frac {1}{10}$
, giving (9.16).
$\mu (E)<\frac {1}{10}$
, giving (9.16).
Let
 $$ \begin{align*}\beta {\, \stackrel{\mathrm{def}}{=}\, } k^{-20 \varepsilon L}, \ \ \ \text{ and write } \ \ \mathcal{P}^{(L)} {\, \stackrel{\mathrm{def}}{=}\, } \bigvee_{i=1}^LT^{-i}(\mathcal{P}).\end{align*} $$
$$ \begin{align*}\beta {\, \stackrel{\mathrm{def}}{=}\, } k^{-20 \varepsilon L}, \ \ \ \text{ and write } \ \ \mathcal{P}^{(L)} {\, \stackrel{\mathrm{def}}{=}\, } \bigvee_{i=1}^LT^{-i}(\mathcal{P}).\end{align*} $$
For each q, we let
![]() $\mathcal {P}^{(L, B)}$
be the elements of
$\mathcal {P}^{(L, B)}$
be the elements of
![]() $\mathcal {P}^{(L)}$
which intersect
$\mathcal {P}^{(L)}$
which intersect
![]() $B=B_{q,L}$
and partition
$B=B_{q,L}$
and partition
![]() $\mathcal {P}^{(L,B)}$
into two subcollections defined by
$\mathcal {P}^{(L,B)}$
into two subcollections defined by
We claim that if
![]() $q \in X_2$
, then
$q \in X_2$
, then
To see this, we note that for q satisfying the conclusion of Proposition 9.2, the cardinality of
![]() $\mathcal {P}^{(L, B)}$
is at most
$\mathcal {P}^{(L, B)}$
is at most
![]() $k^{|\{0 \leq i \leq L \, : \, T^i q \in V\} |}$
. Indeed, for such q, whenever
$k^{|\{0 \leq i \leq L \, : \, T^i q \in V\} |}$
. Indeed, for such q, whenever
![]() $T^i q \notin V$
,
$T^i q \notin V$
,
![]() $T^i\left (B\right )$
is contained in one of the
$T^i\left (B\right )$
is contained in one of the
![]() $P_i$
(and for the other i, we use the obvious bound that
$P_i$
(and for the other i, we use the obvious bound that
![]() $T^iq \in V$
,
$T^iq \in V$
,
![]() $T^i\left (B \right )$
could intersect all of the
$T^i\left (B \right )$
could intersect all of the
![]() $P_i$
). For
$P_i$
). For
![]() $q \in X_2$
, we also have that
$q \in X_2$
, we also have that
![]() $\beta ^{-1/2} \geq k^{|\{0 \leq i \leq L \, : \, T^i q \in V\} |}$
, and this implies that
$\beta ^{-1/2} \geq k^{|\{0 \leq i \leq L \, : \, T^i q \in V\} |}$
, and this implies that
and this proves (9.17).
If
![]() $q \in X_1 \cap X_2$
and
$q \in X_1 \cap X_2$
and
![]() $q' \in B_{q, L} \cap \bigcup \mathcal {P}^{(q,L)}_{\mathrm {big}} $
, then we have
$q' \in B_{q, L} \cap \bigcup \mathcal {P}^{(q,L)}_{\mathrm {big}} $
, then we have
and this implies via (9.12) that
![]() $q' \in W.$
This and (9.17) shows that
$q' \in W.$
This and (9.17) shows that
![]() $X_1 \cap X_2 \subset G_L$
. Thus,
$X_1 \cap X_2 \subset G_L$
. Thus,
and we have shown (9.11).
Proof of Theorem 1.6.
Denote by T the map defined by
![]() $\mathrm {Rel}_{z_0}$
(where defined). Since
$\mathrm {Rel}_{z_0}$
(where defined). Since
![]() $m_{{{\mathcal L}}}$
is G-invariant, it is rotation invariant, and thus
$m_{{{\mathcal L}}}$
is G-invariant, it is rotation invariant, and thus
![]() $m_{{{\mathcal L}}}$
-a.e. q has no horizontal saddle connections. In particular, for such q,
$m_{{{\mathcal L}}}$
-a.e. q has no horizontal saddle connections. In particular, for such q,
![]() $\mathrm {Rel}_z (q)$
is defined for all
$\mathrm {Rel}_z (q)$
is defined for all
![]() $z \in Z$
.
$z \in Z$
.
Assume first that
![]() $m_{{{\mathcal L}}}$
is ergodic. By G-invariance of
$m_{{{\mathcal L}}}$
is ergodic. By G-invariance of
![]() $m_{{\mathcal L}}$
, we have (9.1), so the hypotheses of Theorem 9.1 are satisfied for
$m_{{\mathcal L}}$
, we have (9.1), so the hypotheses of Theorem 9.1 are satisfied for
![]() $\mu = m_{{{\mathcal L}}}$
. Now suppose
$\mu = m_{{{\mathcal L}}}$
. Now suppose
![]() $m_{{{\mathcal L}}}$
is not ergodic, and let
$m_{{{\mathcal L}}}$
is not ergodic, and let
![]() $\mu = \int _{{\mathrm {Prob}}(X)^T} \nu \ d\theta $
be the ergodic decomposition of
$\mu = \int _{{\mathrm {Prob}}(X)^T} \nu \ d\theta $
be the ergodic decomposition of
![]() $\mu $
, where
$\mu $
, where
![]() $\theta $
is a probability measure on
$\theta $
is a probability measure on
![]() ${\mathrm {Prob}}(X)^T$
such that
${\mathrm {Prob}}(X)^T$
such that
![]() $\theta $
-a.e.
$\theta $
-a.e.
![]() $\nu $
is ergodic for T. By Proposition 9.6(2), it suffices to show that the entropy of
$\nu $
is ergodic for T. By Proposition 9.6(2), it suffices to show that the entropy of
![]() $\nu $
is zero for
$\nu $
is zero for
![]() $\theta $
-a.e.
$\theta $
-a.e.
![]() $\nu $
, and thus, we only need to show that assumption (9.1) holds for
$\nu $
, and thus, we only need to show that assumption (9.1) holds for
![]() $\theta $
-a.e.
$\theta $
-a.e.
![]() $\nu $
. This follows from the
$\nu $
. This follows from the
![]() $g_t$
-invariance of
$g_t$
-invariance of
![]() $m_{{{\mathcal L}}}$
. Indeed, by invariance and regularity of
$m_{{{\mathcal L}}}$
. Indeed, by invariance and regularity of
![]() $m_{{{\mathcal L}}}$
, for any
$m_{{{\mathcal L}}}$
, for any
![]() $\varepsilon>0$
, there exists a compact K, so that for all t,
$\varepsilon>0$
, there exists a compact K, so that for all t,
![]() $m_{{{\mathcal L}}}(g_t(K)) =m_{{{\mathcal L}}}(K)>1-\varepsilon ^2$
. Thus, for every t,
$m_{{{\mathcal L}}}(g_t(K)) =m_{{{\mathcal L}}}(K)>1-\varepsilon ^2$
. Thus, for every t,
Thus, for any
![]() $\varepsilon>0$
, there is K so that the set of
$\varepsilon>0$
, there is K so that the set of
![]() $\nu $
, for which
$\nu $
, for which
![]() $(g_{-t_i})_*\nu (K) \geq 1-\varepsilon $
for a sequence
$(g_{-t_i})_*\nu (K) \geq 1-\varepsilon $
for a sequence
![]() $t_i \to \infty $
, has
$t_i \to \infty $
, has
![]() $\theta $
-measure at least
$\theta $
-measure at least
![]() $1-\varepsilon $
. Since
$1-\varepsilon $
. Since
![]() $\varepsilon $
was arbitrary, we have (9.1) for
$\varepsilon $
was arbitrary, we have (9.1) for
![]() $\theta $
-a.e.
$\theta $
-a.e.
![]() $\nu $
.
$\nu $
.
Acknowledgements
We are very grateful to Alex Eskin for crucial contributions to this project. We also thank Simion Filip, Curt McMullen and Alex Wright for useful discussions, we and acknowledge the support of ISF grant 2919/19, BSF grant 2016256, NSFC-ISF grant 3739/21, a Warnock chair, a Simons Fellowship and NSF grants DMS-1452762 and DMS-2055354.
Competing interests
The authors have no competing interest to declare.