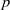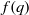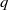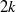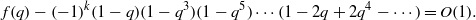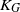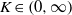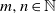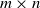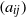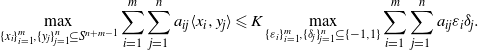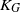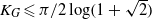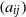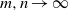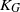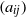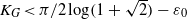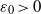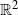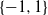The (real) Grothendieck constant 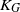 ${K}_{G} $ is the infimum over those
${K}_{G} $ is the infimum over those 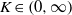 $K\in (0, \infty )$ such that for every
$K\in (0, \infty )$ such that for every 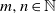 $m, n\in \mathbb{N} $ and every
$m, n\in \mathbb{N} $ and every 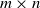 $m\times n$ real matrix
$m\times n$ real matrix 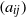 $({a}_{ij} )$ we have
$({a}_{ij} )$ we have 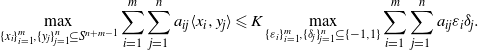 $$\begin{eqnarray*}\displaystyle \max _{\{ x_{i}\} _{i= 1}^{m} , \{ {y}_{j} \} _{j= 1}^{n} \subseteq {S}^{n+ m- 1} }\sum _{i= 1}^{m} \sum _{j= 1}^{n} {a}_{ij} \langle {x}_{i} , {y}_{j} \rangle \leqslant K\max _{\{ \varepsilon _{i}\} _{i= 1}^{m} , \{ {\delta }_{j} \} _{j= 1}^{n} \subseteq \{ - 1, 1\} }\sum _{i= 1}^{m} \sum _{j= 1}^{n} {a}_{ij} {\varepsilon }_{i} {\delta }_{j} . &&\displaystyle\end{eqnarray*}$$
$$\begin{eqnarray*}\displaystyle \max _{\{ x_{i}\} _{i= 1}^{m} , \{ {y}_{j} \} _{j= 1}^{n} \subseteq {S}^{n+ m- 1} }\sum _{i= 1}^{m} \sum _{j= 1}^{n} {a}_{ij} \langle {x}_{i} , {y}_{j} \rangle \leqslant K\max _{\{ \varepsilon _{i}\} _{i= 1}^{m} , \{ {\delta }_{j} \} _{j= 1}^{n} \subseteq \{ - 1, 1\} }\sum _{i= 1}^{m} \sum _{j= 1}^{n} {a}_{ij} {\varepsilon }_{i} {\delta }_{j} . &&\displaystyle\end{eqnarray*}$$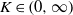 $K\in (0, \infty )$ that is independent of
$K\in (0, \infty )$ that is independent of 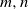 $m, n$ and
$m, n$ and 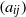 $({a}_{ij} )$. Since Grothendieck’s 1953 discovery of this powerful theorem, it has found numerous applications in a variety of areas, but, despite attracting a lot of attention, the exact value of the Grothendieck constant
$({a}_{ij} )$. Since Grothendieck’s 1953 discovery of this powerful theorem, it has found numerous applications in a variety of areas, but, despite attracting a lot of attention, the exact value of the Grothendieck constant 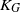 ${K}_{G} $ remains a mystery. The last progress on this problem was in 1977, when Krivine proved that
${K}_{G} $ remains a mystery. The last progress on this problem was in 1977, when Krivine proved that 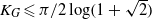 ${K}_{G} \leqslant \pi / 2\log (1+ \sqrt{2} )$ and conjectured that his bound is optimal. Krivine’s conjecture has been restated repeatedly since 1977, resulting in focusing the subsequent research on the search for examples of matrices
${K}_{G} \leqslant \pi / 2\log (1+ \sqrt{2} )$ and conjectured that his bound is optimal. Krivine’s conjecture has been restated repeatedly since 1977, resulting in focusing the subsequent research on the search for examples of matrices 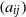 $({a}_{ij} )$ which exhibit (asymptotically, as
$({a}_{ij} )$ which exhibit (asymptotically, as 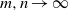 $m, n\rightarrow \infty $) a lower bound on
$m, n\rightarrow \infty $) a lower bound on 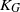 ${K}_{G} $ that matches Krivine’s bound. Here, we obtain an improved Grothendieck inequality that holds for all matrices
${K}_{G} $ that matches Krivine’s bound. Here, we obtain an improved Grothendieck inequality that holds for all matrices 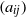 $({a}_{ij} )$ and yields a bound
$({a}_{ij} )$ and yields a bound 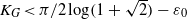 ${K}_{G} \lt \pi / 2\log (1+ \sqrt{2} )- {\varepsilon }_{0} $ for some effective constant
${K}_{G} \lt \pi / 2\log (1+ \sqrt{2} )- {\varepsilon }_{0} $ for some effective constant 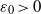 ${\varepsilon }_{0} \gt 0$. Other than disproving Krivine’s conjecture, and along the way also disproving an intermediate conjecture of König that was made in 2000 as a step towards Krivine’s conjecture, our main contribution is conceptual: despite dealing with a binary rounding problem, random two-dimensional projections, when combined with a careful partition of
${\varepsilon }_{0} \gt 0$. Other than disproving Krivine’s conjecture, and along the way also disproving an intermediate conjecture of König that was made in 2000 as a step towards Krivine’s conjecture, our main contribution is conceptual: despite dealing with a binary rounding problem, random two-dimensional projections, when combined with a careful partition of 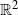 ${ \mathbb{R} }^{2} $ in order to round the projected vectors to values in
${ \mathbb{R} }^{2} $ in order to round the projected vectors to values in 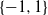 $\{ - 1, 1\} $, perform better than the ubiquitous random hyperplane technique. By establishing the usefulness of higher-dimensional rounding schemes, this fact has consequences in approximation algorithms. Specifically, it yields the best known polynomial-time approximation algorithm for the Frieze–Kannan Cut Norm problem, a generic and well-studied optimization problem with many applications.
$\{ - 1, 1\} $, perform better than the ubiquitous random hyperplane technique. By establishing the usefulness of higher-dimensional rounding schemes, this fact has consequences in approximation algorithms. Specifically, it yields the best known polynomial-time approximation algorithm for the Frieze–Kannan Cut Norm problem, a generic and well-studied optimization problem with many applications.
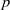 $p$-ADIC HODGE THEORY FOR RIGID-ANALYTIC VARIETIES
$p$-ADIC HODGE THEORY FOR RIGID-ANALYTIC VARIETIES