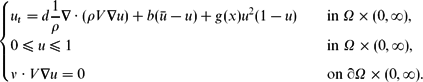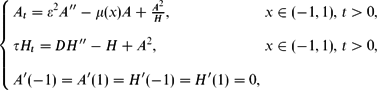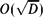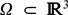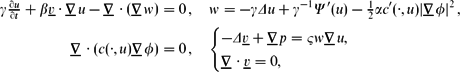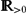Papers
Strong solvability up to clogging of an effective diffusion–precipitation model in an evolving porous medium
-
- Published online by Cambridge University Press:
- 14 April 2016, pp. 179-207
-
- Article
- Export citation
Introduction
Introduction: Big data and partial differential equations†
-
- Published online by Cambridge University Press:
- 07 November 2017, pp. 877-885
-
- Article
-
- You have access
- Export citation
Papers
Unsteady flows induced by a point source or sink in a fluid of finite depth
-
- Published online by Cambridge University Press:
- 22 July 2016, pp. 357-379
-
- Article
- Export citation
Non-local effects in an integro-PDE model from population genetics
-
- Published online by Cambridge University Press:
- 20 November 2015, pp. 1-41
-
- Article
- Export citation
Editorial Announcement
Editorial
-
- Published online by Cambridge University Press:
- 05 September 2017, p. 707
-
- Article
-
- You have access
- Export citation
Papers
A simplified model of glycoprotein production within cell culture
-
- Published online by Cambridge University Press:
- 19 October 2016, pp. 535-561
-
- Article
- Export citation
On the IAA version of the Doi–Edwards model versus the K-BKZ rheological model for polymer fluids: A global existence result for shear flows with small initial data†
-
- Published online by Cambridge University Press:
- 08 January 2016, pp. 42-90
-
- Article
- Export citation
A new analytical approach to consistency and overfitting in regularized empirical risk minimization
- Part of:
-
- Published online by Cambridge University Press:
- 20 July 2017, pp. 886-921
-
- Article
-
- You have access
- Export citation
Obituary
Mathematics in the spirit of Joe Keller
-
- Published online by Cambridge University Press:
- 05 September 2017, pp. 708-715
-
- Article
-
- You have access
- Export citation
Papers
Well-posedness of a diffuse-interface model for two-phase incompressible flows with thermo-induced Marangoni effect
-
- Published online by Cambridge University Press:
- 25 July 2016, pp. 380-434
-
- Article
- Export citation
The mathematics of varistors
-
- Published online by Cambridge University Press:
- 19 May 2016, pp. 208-220
-
- Article
- Export citation
A note on waveless subcritical flow past symmetric bottom topography
-
- Published online by Cambridge University Press:
- 26 October 2016, pp. 562-575
-
- Article
- Export citation
Rate effects on the growth of centres
-
- Published online by Cambridge University Press:
- 07 July 2016, pp. 221-242
-
- Article
-
- You have access
- Open access
- Export citation
Stable spike clusters for the one-dimensional Gierer–Meinhardt system
-
- Published online by Cambridge University Press:
- 08 November 2016, pp. 576-635
-
- Article
-
- You have access
- Open access
- Export citation
Asymptotic behaviour of solutions of free boundary problems for Fisher-KPP equation
-
- Published online by Cambridge University Press:
- 30 August 2016, pp. 435-469
-
- Article
- Export citation
Determining the probability of correct resolution of the left–right ambiguity in towed array sonar
-
- Published online by Cambridge University Press:
- 05 December 2016, pp. 716-735
-
- Article
- Export citation
A contact problem for viscoelastic bodies with inertial effects and unilateral boundary constraints
-
- Published online by Cambridge University Press:
- 07 March 2016, pp. 91-122
-
- Article
- Export citation
On the game p-Laplacian on weighted graphs with applications in image processing and data clustering†
-
- Published online by Cambridge University Press:
- 03 July 2017, pp. 922-948
-
- Article
-
- You have access
- Export citation
Non-local Cahn–Hilliard equations with fractional dynamic boundary conditions
-
- Published online by Cambridge University Press:
- 01 December 2016, pp. 736-788
-
- Article
- Export citation
Stable finite element approximation of a Cahn–Hilliard–Stokes system coupled to an electric field
-
- Published online by Cambridge University Press:
- 09 September 2016, pp. 470-498
-
- Article
- Export citation