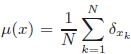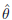Volume 18 - 2014
Research Article
Nonparametric regression estimation based on spatially inhomogeneous data: minimax global convergence rates and adaptivity
-
- Published online by Cambridge University Press:
- 06 December 2013, pp. 1-41
-
- Article
- Export citation
Wavelet estimation of the long memory parameter for Hermite polynomial of Gaussian processes∗∗∗
-
- Published online by Cambridge University Press:
- 28 November 2013, pp. 42-76
-
- Article
- Export citation
Model selection and estimation of a component in additive regression
-
- Published online by Cambridge University Press:
- 28 November 2013, pp. 77-116
-
- Article
- Export citation
Upper large deviations for maximal flows through a tilted cylinder
-
- Published online by Cambridge University Press:
- 28 November 2013, pp. 117-129
-
- Article
- Export citation
Density smoothness estimation problem using a wavelet approach
-
- Published online by Cambridge University Press:
- 28 November 2013, pp. 130-144
-
- Article
- Export citation
Survival probabilities of autoregressive processes
-
- Published online by Cambridge University Press:
- 28 November 2013, pp. 145-170
-
- Article
- Export citation
On the time constant in a dependent first passage percolation model
-
- Published online by Cambridge University Press:
- 27 March 2014, pp. 171-184
-
- Article
- Export citation
Means in complete manifolds: uniqueness and approximation
-
- Published online by Cambridge University Press:
- 27 March 2014, pp. 185-206
-
- Article
- Export citation
On identifiability of mixtures of independent distribution laws∗∗∗∗∗∗
-
- Published online by Cambridge University Press:
- 01 July 2014, pp. 207-232
-
- Article
- Export citation
Adding constraints to BSDEs with jumps: an alternative to multidimensional reflections∗
-
- Published online by Cambridge University Press:
- 01 July 2014, pp. 233-250
-
- Article
- Export citation
Unbiased risk estimation method for covariance estimation
-
- Published online by Cambridge University Press:
- 25 July 2014, pp. 251-264
-
- Article
- Export citation
Uniform Confidence Bands for Local Polynomial Quantile Estimators∗
-
- Published online by Cambridge University Press:
- 25 July 2014, pp. 265-276
-
- Article
- Export citation
Estimation in autoregressive model with measurement error
-
- Published online by Cambridge University Press:
- 03 October 2014, pp. 277-307
-
- Article
- Export citation
Moderate deviations for the Durbin–Watson statistic related to the first-order autoregressive process
-
- Published online by Cambridge University Press:
- 03 October 2014, pp. 308-331
-
- Article
- Export citation
Consistent non-parametric Bayesian estimation for a time-inhomogeneous Brownian motion∗
-
- Published online by Cambridge University Press:
- 03 October 2014, pp. 332-341
-
- Article
- Export citation
Asymptotic normality and efficiency of two Sobol index estimators
-
- Published online by Cambridge University Press:
- 03 October 2014, pp. 342-364
-
- Article
- Export citation
Random coefficients bifurcating autoregressive processes
-
- Published online by Cambridge University Press:
- 03 October 2014, pp. 365-399
-
- Article
- Export citation
Adaptive estimation of a density function using beta kernels
-
- Published online by Cambridge University Press:
- 08 October 2014, pp. 400-417
-
- Article
- Export citation
From almost sure local regularity to almost sure Hausdorff dimension for Gaussian fields
-
- Published online by Cambridge University Press:
- 08 October 2014, pp. 418-440
-
- Article
- Export citation
General approximation method for the distribution of Markov processes conditioned not to be killed
-
- Published online by Cambridge University Press:
- 08 October 2014, pp. 441-467
-
- Article
- Export citation