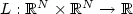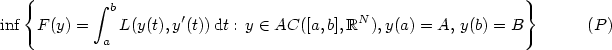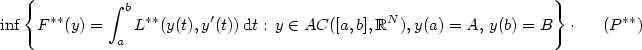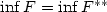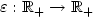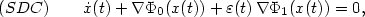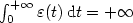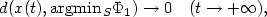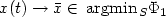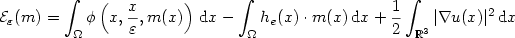Research Article
Stability rates for patchy vector fields
-
- Published online by Cambridge University Press:
- 15 March 2004, pp. 168-200
-
- Article
- Export citation
A relaxation result for autonomous integral functionals with discontinuous non-coercive integrand
-
- Published online by Cambridge University Press:
- 15 March 2004, pp. 201-210
-
- Article
- Export citation
On the Paneitz energy on standard three sphere
-
- Published online by Cambridge University Press:
- 15 March 2004, pp. 211-223
-
- Article
- Export citation
An approximation theorem for sequences of linear strains and its applications
-
- Published online by Cambridge University Press:
- 15 March 2004, pp. 224-242
-
- Article
- Export citation
The steepest descent dynamical system with control. Applications to constrained minimization
-
- Published online by Cambridge University Press:
- 15 March 2004, pp. 243-258
-
- Article
- Export citation
A set oriented approach to global optimal control
-
- Published online by Cambridge University Press:
- 15 March 2004, pp. 259-270
-
- Article
- Export citation
Viscosity solutions for an optimal control problem with Preisach hysteresis nonlinearities
-
- Published online by Cambridge University Press:
- 15 March 2004, pp. 271-294
-
- Article
- Export citation
Homogenization of micromagnetics large bodies
-
- Published online by Cambridge University Press:
- 15 March 2004, pp. 295-314
-
- Article
- Export citation