Let H be a real Hilbert space, $\Phi_1: H\to \xR$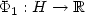 a convex function of class ${\mathcal C}^1$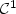 that we wish to minimize under the convex constraint S. A classical approach consists in following the trajectories of the generalized steepest descent system (cf.   Brézis [CITE]) applied to the non-smooth function $\Phi_1+\delta_S$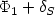. Following Antipin [1], it is also possible to use a continuous gradient-projection system. We propose here an alternative method as follows: given a smooth convex function $\Phi_0: H\to \xR$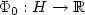 whose critical points coincide with S and a control parameter $\varepsilon:\xR_+\to \xR_+$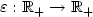 tending to zero, we consider the “Steepest Descent and Control” system \[(SDC) \qquad \dot{x}(t)+\nabla \Phi_0(x(t))+\varepsilon(t)\, \nabla \Phi_1(x(t))=0,\]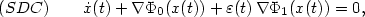 where the control ε satisfies $\int_0^{+\infty} \varepsilon(t)\, {\rm d}t =+\infty$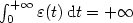. This last condition ensures that ε “slowly” tends to 0. When H is finite dimensional, we then prove that $d(x(t), {\rm argmin}\kern 0.12em_S \Phi_1) \to 0 \quad (t\to +\infty),$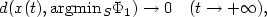 and we give sufficient conditions under which $x(t) \to \bar{x}\in \,{\rm argmin}\kern 0.12em_S \Phi_1$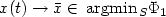. We end the paper by numerical experiments allowing to compare the (SDC) system with the other systems already mentioned.