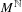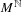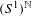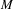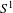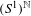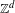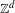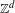Research Article
Classification and rigidity of totally periodic pseudo-Anosov flows in graph manifolds
-
- Published online by Cambridge University Press:
- 03 July 2014, pp. 1681-1722
-
- Article
- Export citation
Li–Yorke chaos in linear dynamics
-
- Published online by Cambridge University Press:
- 10 July 2014, pp. 1723-1745
-
- Article
- Export citation
Lower bound in the Roth theorem for amenable groups
-
- Published online by Cambridge University Press:
- 03 July 2014, pp. 1746-1766
-
- Article
- Export citation
Suffix conjugates for a class of morphic subshifts
-
- Published online by Cambridge University Press:
- 04 June 2014, pp. 1767-1782
-
- Article
- Export citation
Affine almost automorphic actions on compact nilmanifolds
-
- Published online by Cambridge University Press:
- 05 August 2014, pp. 1783-1794
-
- Article
- Export citation
Genus-one Birkhoff sections for geodesic flows
-
- Published online by Cambridge University Press:
- 11 August 2014, pp. 1795-1813
-
- Article
- Export citation
Skew products, quantitative recurrence, shrinking targets and decay of correlations
-
- Published online by Cambridge University Press:
- 03 July 2014, pp. 1814-1845
-
- Article
- Export citation
A family of rational maps with buried Julia components
-
- Published online by Cambridge University Press:
- 03 July 2014, pp. 1846-1879
-
- Article
- Export citation
Positive topological entropy for monotone recurrence relations
-
- Published online by Cambridge University Press:
- 30 June 2014, pp. 1880-1901
-
- Article
- Export citation
Example of a non-standard extreme-value law
-
- Published online by Cambridge University Press:
- 04 June 2014, pp. 1902-1912
-
- Article
- Export citation
Shapes of polynomial Julia sets
-
- Published online by Cambridge University Press:
- 04 August 2014, pp. 1913-1924
-
- Article
- Export citation
Entropy and variational principle for one-dimensional lattice systems with a general a priori probability: positive and zero temperature
-
- Published online by Cambridge University Press:
- 03 July 2014, pp. 1925-1961
-
- Article
- Export citation
One-dimensional projective subdynamics of uniformly mixing
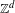 $\mathbb{Z}^{d}$ shifts of finite type
$\mathbb{Z}^{d}$ shifts of finite type
-
- Published online by Cambridge University Press:
- 03 July 2014, pp. 1962-1999
-
- Article
- Export citation
Hölder shadowing on finite intervals
-
- Published online by Cambridge University Press:
- 30 June 2014, pp. 2000-2016
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
ETS volume 35 Issue 6 Cover and Front matter
-
- Published online by Cambridge University Press:
- 30 July 2015, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
ETS volume 35 Issue 6 Cover and Back matter
-
- Published online by Cambridge University Press:
- 30 July 2015, pp. b1-b2
-
- Article
-
- You have access
- Export citation