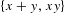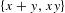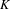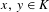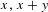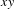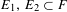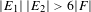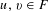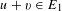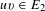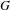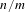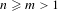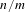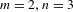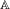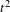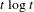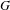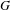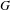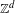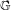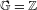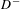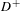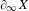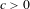Research Article
Ergodic theorem involving additive and multiplicative groups of a field and
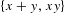 $\{x+y,xy\}$ patterns
$\{x+y,xy\}$ patterns
-
- Published online by Cambridge University Press:
- 06 October 2015, pp. 673-692
-
- Article
- Export citation
Return words of linear involutions and fundamental groups
-
- Published online by Cambridge University Press:
- 28 December 2015, pp. 693-715
-
- Article
- Export citation
Markov partitions and homology for
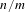 $n/m$-solenoids
$n/m$-solenoids
-
- Published online by Cambridge University Press:
- 27 November 2015, pp. 716-738
-
- Article
- Export citation
Ziggurat fringes are self-similar
-
- Published online by Cambridge University Press:
- 28 December 2015, pp. 739-757
-
- Article
- Export citation
Criteria for the density of the graph of the entropy map restricted to ergodic states
-
- Published online by Cambridge University Press:
- 29 January 2016, pp. 758-785
-
- Article
- Export citation
Flow equivalence of sofic beta-shifts
-
- Published online by Cambridge University Press:
- 28 January 2016, pp. 786-801
-
- Article
- Export citation
Entropy estimate by a randomness criterion
-
- Published online by Cambridge University Press:
- 28 January 2016, pp. 802-823
-
- Article
- Export citation
The critical dimension for
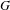 $G$-measures
$G$-measures
-
- Published online by Cambridge University Press:
- 21 October 2015, pp. 824-836
-
- Article
- Export citation
Direct topological factorization for topological flows
-
- Published online by Cambridge University Press:
- 27 November 2015, pp. 837-858
-
- Article
- Export citation
On multicorns and unicorns II: bifurcations in spaces of antiholomorphic polynomials
-
- Published online by Cambridge University Press:
- 27 November 2015, pp. 859-899
-
- Article
- Export citation
Counting common perpendicular arcs in negative curvature
-
- Published online by Cambridge University Press:
- 28 January 2016, pp. 900-938
-
- Article
- Export citation
Flat strips, Bowen–Margulis measures, and mixing of the geodesic flow for rank one CAT(0) spaces
-
- Published online by Cambridge University Press:
- 28 December 2015, pp. 939-970
-
- Article
- Export citation
Coupling methods for random topological Markov chains
-
- Published online by Cambridge University Press:
- 20 October 2015, pp. 971-994
-
- Article
- Export citation
Whirly 3-interval exchange transformations
-
- Published online by Cambridge University Press:
- 20 October 2015, pp. 995-1008
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
ETS volume 37 Issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 29 March 2017, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
ETS volume 37 Issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 29 March 2017, pp. b1-b2
-
- Article
-
- You have access
- Export citation