Hostname: page-component-76fb5796d-skm99 Total loading time: 0 Render date: 2024-04-25T09:51:38.564Z Has data issue: false hasContentIssue false
  • English
  • Français

Counting common perpendicular arcs in negative curvature

Published online by Cambridge University Press:  28 January 2016

JOUNI PARKKONEN  and
FRÉDÉRIC PAULIN
JOUNI PARKKONEN
Affiliation:
Department of Mathematics and Statistics, PO Box 35, 40014University of Jyväskylä, Finland email jouni.t.parkkonen@jyu.fi
FRÉDÉRIC PAULIN
Affiliation:
Département de mathématique, UMR 8628 CNRS, Bât. 425, Université Paris-Sud, 91405 ORSAY Cedex, France email frederic.paulin@math.u-psud.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 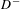$D^{-}$ and 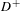$D^{+}$ be properly immersed closed locally convex subsets of a Riemannian manifold with pinched negative sectional curvature. Using mixing properties of the geodesic flow, we give an asymptotic formula as 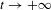$t\rightarrow +\infty$ for the number of common perpendiculars of length at most $t$ from 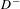$D^{-}$ to 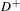$D^{+}$, counted with multiplicities, and we prove the equidistribution in the outer and inner unit normal bundles of 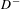$D^{-}$ and 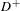$D^{+}$ of the tangent vectors at the endpoints of the common perpendiculars. When the manifold is compact with exponential decay of correlations or arithmetic with finite volume, we give an error term for the asymptotic. As an application, we give an asymptotic formula for the number of connected components of the domain of discontinuity of Kleinian groups as their diameter goes to $0$.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 3 , May 2017 , pp. 900 - 938
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abikoff, W.. On boundaries of Teichmüller spaces and on Kleinian groups III. Acta Math. 134 (1975), 211–237.Google Scholar
Babillot, M.. On the mixing property for hyperbolic systems. Israel J. Math. 129 (2002), 61–76.Google Scholar
Ballmann, W.. Lectures on Spaces of Nonpositive Curvature (DMW Seminar, 25) . Birkhäuser, 1995.CrossRefGoogle Scholar
Beardon, A. F.. The Geometry of Discrete Groups (Graduate Texts in Mathematics, 91) . Springer, 1983.Google Scholar
Bowditch, B.. Geometrical finiteness with variable negative curvature. Duke Math. J. 77 (1995), 229–274.Google Scholar
Broise-Alamichel, A., Parkkonen, J. and Paulin, F.. Equidistribution and counting under equilibrium states and in quantum graphs, with applications to non-Archimedean Diophantine approximation. In preparation.Google Scholar
Bridson, M. R. and Haefliger, A.. Metric Spaces of Non-positive Curvature (Grundlehren der mathematischen Wissenschaften, 319) . Springer, 1999.CrossRefGoogle Scholar
M. Brin. Ergodicity of the geodesic flow. Appendix in W. Ballmann. Lectures on Spaces of Nonpositive Curvature (DMV Seminar, 25). Birkhäuser, 1995, pp. 81–95.Google Scholar
Canary, R. D. and Taylor, E.. Kleinian groups with small limit sets. Duke Math. J. 73 (1994), 371–381.Google Scholar
Clozel, L.. Démonstration de la conjecture 𝜏. Invent. Math. 151 (2003), 297–328.Google Scholar
Cosentino, S.. Equidistribution of parabolic fixed points in the limit set of Kleinian groups. Ergod. Th. & Dynam. Sys. 19 (1999), 1437–1484.Google Scholar
Dal’Bo, F.. Remarques sur le spectre des longueurs d’une surface et comptage. Bol. Soc. Brasil. Math. 30 (1999), 199–221.Google Scholar
Dal’Bo, F.. Topologie du feuilletage fortement stable. Ann. Inst. Fourier (Grenoble) 50 (2000), 981–993.Google Scholar
Dolgopyat, D.. On decay of correlation in Anosov flows. Ann. of Math. (2) 147 (1998), 357–390.Google Scholar
Dal’Bo, F., Otal, J.-P. and Peigné, M.. Séries de Poincaré des groupes géométriquement finis. Israel J. Math. 118 (2000), 109–124.Google Scholar
Eskin, A. and McMullen, C.. Mixing, counting, and equidistribution in Lie groups. Duke Math. J. 71 (1993), 181–209.Google Scholar
Giulietti, P., Liverani, C. and Pollicott, M.. Anosov flows and dynamical zeta functions. Ann. of Math. (2) 178 (2013), 687–773.Google Scholar
Goldman, W. M.. Complex Hyperbolic Geometry. Oxford University Press, 1999.Google Scholar
Hamenstädt, U.. A new description of the Bowen–Margulis measure. Ergod. Th. & Dynam. Sys. 9 (1989), 455–464.Google Scholar
Herrmann, O.. Über die Verteilung der Längen geodätischer Lote in hyperbolischen Raumformen. Math. Z. 79 (1962), 323–343.Google Scholar
Hersonsky, S. and Paulin, F.. On the rigidity of discrete isometry groups of negatively curved spaces. Comment. Math. Helv. 72 (1997), 349–388.Google Scholar
Hersonsky, S. and Paulin, F.. Counting orbit points in coverings of negatively curved manifolds and Hausdorff dimension of cusp excursions. Ergod. Th. & Dynam. Sys. 24 (2004), 803–824.CrossRefGoogle Scholar
Huber, H.. Über eine neue Klasse automorpher Funktionen und ein Gitterpunktproblem in der hyperbolischen Ebene. I. Comment. Math. Helv. 30 (1956), 20–62.Google Scholar
Huber, H.. Zur analytischen Theorie hyperbolischen Raumformen und Bewegungsgruppen. Math. Ann. 138 (1959), 1–26.Google Scholar
Kapovich, M.. Hyperbolic Manifolds and Discrete Groups (Progress in Mathematics, 183) . Birkhäuser, 2001.Google Scholar
Kim, I.. Counting, mixing and equidistribution of horospheres in geometrically finite rank one locally symmetric manifolds. J. Reine Angew. Math. 704 (2015), 85–133.Google Scholar
Kleinbock, D. and Margulis, G.. Bounded orbits of nonquasiunipotent flows on homogeneous spaces. Sinai’s Moscow Seminar on Dynamical Systems (American Mathematical Society Translations, Series, 171) . American Mathematical Society, 1996, pp. 141–172.Google Scholar
Kleinbock, D. and Margulis, G.. Logarithm laws for flows on homogeneous spaces. Invent. Math. 138 (1999), 451–494.Google Scholar
Kontorovich, A.. The hyperbolic lattice point count in infinite volume with applications to sieves. Duke Math. J. 149 (2009), 1–36.Google Scholar
Kontorovich, A. and Oh, H.. Apollonian circle packings and closed horospheres on hyperbolic 3-manifolds. J. Amer. Math. Soc. 24 (2011), 603–648.Google Scholar
Lax, P. D. and Phillips, R. S.. The asymptotic distribution of lattice points in Euclidean and non-Euclidean spaces. J. Funct. Anal. 46 (1982), 280–350.Google Scholar
Lee, M. and Oh, H.. Effective circle count for Apollonian packings and closed horospheres. Geom. Funct. Anal. 23 (2013), 580–621.Google Scholar
Martin, K., McKee, M. and Wambach, E.. A relative trace formula for a compact Riemann surface. Int. J. Number Theory 7 (2011), 389–429; see webpage of first author for an erratum.Google Scholar
Margulis, G.. Applications of ergodic theory for the investigation of manifolds of negative curvature. Funct. Anal. Appl. 3 (1969), 335–336.Google Scholar
Maskit, B.. Kleinian Groups (Grundlehren der mathematischen Wissenschaften, 287) . Springer, 1988.Google Scholar
Matsuzaki, K. and Taniguchi, M.. Hyperbolic Manifolds and Kleinian Groups. Oxford University Press, 1998.Google Scholar
Mohammadi, A. and Oh, H.. Matrix coefficients, counting and primes for orbits of geometrically finite groups. J. Eur. Math. Soc. 17 (2015), 837–897.CrossRefGoogle Scholar
Moore, C.. Exponential decay of correlation coefficients for geodesic flows. Group Representations, Ergodic Theory, Operator Algebras, and Mathematical Physics (Berkeley, 1984) (Mathematical Sciences Research Institute Publications, 6) . Springer, New York, 1987, pp. 163–181.Google Scholar
Oh, H. and Shah, N.. The asymptotic distribution of circles in the orbits of Kleinian groups. Invent. Math. 187 (2012), 1–35.Google Scholar
Oh, H. and Shah, N.. Equidistribution and counting for orbits of geometrically finite hyperbolic groups. J. Amer. Math. Soc. 26 (2013), 511–562.Google Scholar
Oh, H. and Shah, N.. Counting visible circles on the sphere and Kleinian groups. Geometry, Topology and Dynamics in Negative Curvature (ICM 2010 Satellite Conference, Bangalore) (London Mathematical Society Lecture Notes, 425). Eds. C. S. Aravinda, T. Farrell and J.-F. Lafont. Cambridge University Press, Cambridge, 2016, pp. 272–288.Google Scholar
Parkkonen, J. and Paulin, F.. Prescribing the behaviour of geodesics in negative curvature. Geom. Topol. 14 (2010), 277–392.CrossRefGoogle Scholar
Parkkonen, J. and Paulin, F.. Spiraling spectra of geodesic lines in negatively curved manifolds. Math. Z. 268 (2011), 101–142; Erratum: Math. Z. 276 (2014), 1215–1216.Google Scholar
Parkkonen, J. and Paulin, F.. Équidistribution, comptage et approximation par irrationnels quadratiques. J. Mod. Dyn. 6 (2012), 1–40.Google Scholar
Parkkonen, J. and Paulin, F.. On strictly convex subsets in negatively curved manifolds. J. Geom. Anal. 22 (2012), 621–632.Google Scholar
Parkkonen, J. and Paulin, F.. Skinning measures in negative curvature and equidistribution of equidistant submanifolds. Ergod. Th. & Dynam. Sys. 34 (2014), 1310–1342.CrossRefGoogle Scholar
Parkkonen, J. and Paulin, F.. On the arithmetic of crossratios and generalised Mertens’ formulas. Numéro Spécial ‘Aux croisements de la géométrie hyperbolique et de l’arithmétique’ (Annales de la Faculté des Sciences de Toulouse, 23) . Eds. Dal’Bo, F. and Lecuire, C.. 2014, pp. 967–1022.Google Scholar
Parkkonen, J. and Paulin, F.. On the hyperbolic orbital counting problem in conjugacy classes. Math. Z. 279 (2015), 1175–1196.Google Scholar
Parkkonen, J. and Paulin, F.. Counting arcs in negative curvature. Geometry, Topology and Dynamics in Negative Curvature (ICM 2010 Satellite Conference, Bangalore) (London Mathematical Society Lecture Notes, 425). Eds. C. S. Aravinda, T. Farrell and J.-F. Lafont, Cambridge University Press, Cambridge, 2016, pp. 289–340.Google Scholar
Parkkonen, J. and Paulin, F.. Counting and equidistribution in Heisenberg groups. Preprint, 2014,arXiv:1402.7225 [hal-00955576], Math. Ann., to appear.Google Scholar
Pollicott, M.. The Schottky–Klein prime function and counting functions for Fenchel double crosses. Preprint, 2011.Google Scholar
Paulin, F., Pollicott, M. and Schapira, B.. Equilibrium States in Negative Curvature (Astérisque, 373), Société Mathématique de France, Paris, 2015.Google Scholar
Roblin, T.. Ergodicité et équidistribution en courbure négative. Mém. Soc. Math. Fr. 95 (2003).Google Scholar
Walter, R.. Some analytical properties of geodesically convex sets. Abh. Math. Semin. Univ. Hambg. 45 (1976), 263–282.Google Scholar