Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Frantzikinakis, Nikos
2015.
Multiple correlation sequences and nilsequences.
Inventiones mathematicae,
Vol. 202,
Issue. 2,
p.
875.
Huang, Wen
Lian, Zhengxing
Shao, Song
and
Ye, Xiangdong
2017.
Sequences from zero entropy noncommutative toral automorphisms and Sarnak Conjecture.
Journal of Differential Equations,
Vol. 263,
Issue. 1,
p.
779.
KOUTSOGIANNIS, ANDREAS
2018.
Integer part polynomial correlation sequences.
Ergodic Theory and Dynamical Systems,
Vol. 38,
Issue. 4,
p.
1525.
Bergelson, V.
and
Leibman, A.
2018.
IPr⁎-recurrence and nilsystems.
Advances in Mathematics,
Vol. 339,
Issue. ,
p.
642.
FRANTZIKINAKIS, NIKOS
and
HOST, BERNARD
2018.
Weighted multiple ergodic averages and correlation sequences.
Ergodic Theory and Dynamical Systems,
Vol. 38,
Issue. 1,
p.
81.
BERGELSON, V.
and
LEIBMAN, A.
2018.
Sets of large values of correlation functions for polynomial cubic configurations.
Ergodic Theory and Dynamical Systems,
Vol. 38,
Issue. 2,
p.
499.
Tao, Terence
and
Teräväinen, Joni
2019.
The structure of logarithmically averaged correlations of multiplicative functions, with applications to the Chowla and Elliott conjectures.
Duke Mathematical Journal,
Vol. 168,
Issue. 11,
Tao, Terence
and
Teräväinen, Joni
2019.
The structure of correlations of multiplicative functions at almost all scales, with applications to the Chowla and Elliott conjectures.
Algebra & Number Theory,
Vol. 13,
Issue. 9,
p.
2103.
EISNER, TANJA
2020.
Nilsystems and ergodic averages along primes.
Ergodic Theory and Dynamical Systems,
Vol. 40,
Issue. 10,
p.
2769.
LE, ANH NGOC
2020.
Nilsequences and multiple correlations along subsequences.
Ergodic Theory and Dynamical Systems,
Vol. 40,
Issue. 6,
p.
1634.
Koutsogiannis, Andreas
Le, Anh
Moreira, Joel
and
Richter, Florian
2020.
Structure of multicorrelation sequences with integer part polynomial iterates along primes.
Proceedings of the American Mathematical Society,
Vol. 149,
Issue. 1,
p.
209.
Moragues, Andreu Ferré
2021.
Properties of multicorrelation sequences and large returns under some ergodicity assumptions.
Discrete & Continuous Dynamical Systems,
Vol. 41,
Issue. 6,
p.
2809.
Frantzikinakis, Nikos
and
Host, Bernard
2021.
Furstenberg Systems of Bounded Multiplicative Functions and Applications.
International Mathematics Research Notices,
Vol. 2021,
Issue. 8,
p.
6077.
Bergelson, Vitaly
Downarowicz, Tomasz
and
Vandehey, Joseph
2022.
Deterministic functions on amenable semigroups and a generalization of the Kamae-Weiss theorem on normality preservation.
Journal d'Analyse Mathématique,
Vol. 148,
Issue. 1,
p.
213.
Le, Anh N.
2022.
Sublacunary sets and interpolation sets for nilsequences.
Discrete & Continuous Dynamical Systems,
Vol. 42,
Issue. 4,
p.
1855.
ACKELSBERG, ETHAN
and
BERGELSON, VITALY
2024.
Multiple recurrence and popular differences for polynomial patterns in rings of integers.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 176,
Issue. 2,
p.
239.
DONOSO, SEBASTIÁN
FERRÉ MORAGUES, ANDREU
KOUTSOGIANNIS, ANDREAS
and
SUN, WENBO
2024.
Decomposition of multicorrelation sequences and joint ergodicity.
Ergodic Theory and Dynamical Systems,
Vol. 44,
Issue. 2,
p.
432.
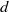 $d$-parameter) basic nilsequence is a sequence of the form
$d$-parameter) basic nilsequence is a sequence of the form 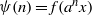 $\psi (n)= f({a}^{n} x)$,
$\psi (n)= f({a}^{n} x)$,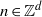 $n\in { \mathbb{Z} }^{d} $, where
$n\in { \mathbb{Z} }^{d} $, where  $x$ is a point of a compact nilmanifold
$x$ is a point of a compact nilmanifold 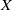 $X$,
$X$,  $a$ is a translation on
$a$ is a translation on 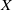 $X$, and
$X$, and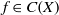 $f\in C(X)$; a nilsequence is a uniform limit of basic nilsequences. If
$f\in C(X)$; a nilsequence is a uniform limit of basic nilsequences. If 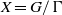 $X= G/ \Gamma $ is a compact nilmanifold,
$X= G/ \Gamma $ is a compact nilmanifold, 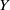 $Y$ is a subnilmanifold of
$Y$ is a subnilmanifold of 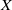 $X$,
$X$, 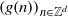 $\mathop{(g(n))}\nolimits_{n\in { \mathbb{Z} }^{d} } $ is a polynomial sequence in
$\mathop{(g(n))}\nolimits_{n\in { \mathbb{Z} }^{d} } $ is a polynomial sequence in 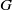 $G$, and
$G$, and 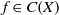 $f\in C(X)$, we show that the sequence
$f\in C(X)$, we show that the sequence 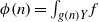 $\phi (n)= \int \nolimits \nolimits_{g(n)Y} f$ is the sum of a basic nilsequence and a sequence that converges to zero in uniform density (a null-sequence). We also show that an integral of a family of nilsequences is a nilsequence plus a null-sequence. We deduce that for any invertible finite measure preserving system
$\phi (n)= \int \nolimits \nolimits_{g(n)Y} f$ is the sum of a basic nilsequence and a sequence that converges to zero in uniform density (a null-sequence). We also show that an integral of a family of nilsequences is a nilsequence plus a null-sequence. We deduce that for any invertible finite measure preserving system 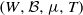 $(W, \mathcal{B} , \mu , T)$, polynomials
$(W, \mathcal{B} , \mu , T)$, polynomials 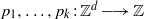 ${p}_{1} , \ldots , {p}_{k} : { \mathbb{Z} }^{d} \longrightarrow \mathbb{Z} $, and sets
${p}_{1} , \ldots , {p}_{k} : { \mathbb{Z} }^{d} \longrightarrow \mathbb{Z} $, and sets 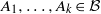 ${A}_{1} , \ldots , {A}_{k} \in \mathcal{B} $, the sequence
${A}_{1} , \ldots , {A}_{k} \in \mathcal{B} $, the sequence 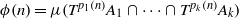 $\phi (n)= \mu ({T}^{{p}_{1} (n)} {A}_{1} \cap \cdots \cap {T}^{{p}_{k} (n)} {A}_{k} )$,
$\phi (n)= \mu ({T}^{{p}_{1} (n)} {A}_{1} \cap \cdots \cap {T}^{{p}_{k} (n)} {A}_{k} )$, 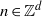 $n\in { \mathbb{Z} }^{d} $, is the sum of a nilsequence and a null-sequence.
$n\in { \mathbb{Z} }^{d} $, is the sum of a nilsequence and a null-sequence.



