Article contents
On graph products of multipliers and the Haagerup property for 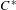 $C^{\ast }$-dynamical systems
$C^{\ast }$-dynamical systems
Published online by Cambridge University Press: 07 August 2019
Abstract
We consider the notion of the graph product of actions of discrete groups 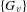 $\{G_{v}\}$ on a
$\{G_{v}\}$ on a 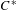 $C^{\ast }$-algebra
$C^{\ast }$-algebra 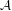 ${\mathcal{A}}$ and show that under suitable commutativity conditions the graph product action
${\mathcal{A}}$ and show that under suitable commutativity conditions the graph product action 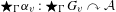 $\star _{\unicode[STIX]{x1D6E4}}\unicode[STIX]{x1D6FC}_{v}:\star _{\unicode[STIX]{x1D6E4}}G_{v}\curvearrowright {\mathcal{A}}$ has the Haagerup property if each action
$\star _{\unicode[STIX]{x1D6E4}}\unicode[STIX]{x1D6FC}_{v}:\star _{\unicode[STIX]{x1D6E4}}G_{v}\curvearrowright {\mathcal{A}}$ has the Haagerup property if each action 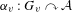 $\unicode[STIX]{x1D6FC}_{v}:G_{v}\curvearrowright {\mathcal{A}}$ possesses the Haagerup property. This generalizes the known results on graph products of groups with the Haagerup property. To accomplish this, we introduce the graph product of multipliers associated to the actions and show that the graph product of positive-definite multipliers is positive definite. These results have impacts on left-transformation groupoids and give an alternative proof of a known result for coarse embeddability. We also record a cohomological characterization of the Haagerup property for group actions.
$\unicode[STIX]{x1D6FC}_{v}:G_{v}\curvearrowright {\mathcal{A}}$ possesses the Haagerup property. This generalizes the known results on graph products of groups with the Haagerup property. To accomplish this, we introduce the graph product of multipliers associated to the actions and show that the graph product of positive-definite multipliers is positive definite. These results have impacts on left-transformation groupoids and give an alternative proof of a known result for coarse embeddability. We also record a cohomological characterization of the Haagerup property for group actions.
Keywords
- Type
- Original Article
- Information
- Copyright
- © Cambridge University Press, 2019
References
- 1
- Cited by





