INTRODUCTION
The notion that many infectious diseases such as influenza, measles and chickenpox [Reference Becker1] exhibit repetitive or regular behaviour over time is of vital importance. In order to guide planning for future disease outbreaks, there has been considerable interest in applying mathematical and statistical models to elucidate the underlying mechanism of cyclical behaviour. Time-domain methods [Reference Liu2–Reference José and Bishop4], a regression of the present based on the past, such as the seasonal autoregressive integrated moving average (SARIMA) model [Reference Box and Jenkins5] and the generalized autoregressive conditional heteroskedasticity (GARCH) model [Reference Bollerslev6], appear elegant in practice since they provide a view of nature in terms of intuitive linear forms. However, these models are at risk of over-differencing [Reference Cai7] (which indicates the abuse of differencing methods leading to heavy loss of information) and over-fitting [Reference Box and Jenkins5] (which means fitting too many redundant parameters). More importantly, these modelling approaches assume linearity of variables [Reference Ture and Kurt8], whereas the inherent structure of epidemic mechanisms is often nonlinear [Reference Olsen and Schaffer9]. Thus, an alternative method for time-series analysis is needed.
Spectral analysis is based on the decomposition of an empirical series into regular components [Reference Shumway10]. From the view of regression, spectral analysis models may be considered as a regression of the present on periodic sines and cosines. A main advantage of this model lies in its capability to explain the dynamics of some infectious diseases. For example, José & Bishop [Reference José and Bishop4] compared a SARIMA model and the power spectral density method to characterize the overall dynamics of rotavirus infections as a whole and that of serotypes G1, G2, G3, G4 and G9 individually. According to that study, although the SARIMA model detected no obvious discernible pattern of dynamics except for the annual cycle, the spectral analysis did, in fact, capture seasonal, biannual and quinquennial periods.
As spectral analysis is becoming increasingly indispensable in biomedicine and epidemiology [Reference Cai, Xu and Baumketner11–Reference Dillenseger and Esneault13], some barriers to this method have been noted that may affect its application. First, some spectral approaches are too empirical to be appropriate. For example, the cyclical regression models [Reference Lui and Kendal14] require frequency parameters to be preset. This is inappropriate, especially when the seasonal patterns remain elusive. Second, some analyses focus on the separate estimation method [Reference Sumi and Kamo15], which, in fact, consists of two separate steps: (1) to obtain the frequency parameter by means of the maximum entropy method (MEM); and (2) to utilize least squares fitting (LSF) to estimate the incidence curve. Such methods are simple, but their efficiency is yet to be demonstrated [Reference Tsay16]. The joint estimation procedure seems more efficient. However, to our knowledge, joint estimation remains a daunting task in the frequency domain [Reference Ma17, Reference Lin18]. Third, as claimed by Luo et al. [Reference Luo19]: with its origins in electrical engineering science, spectral analysis requires adequate mathematical and physical expertise which, unfortunately, presents an obstacle for many epidemiological researchers and practitioners.
Therefore, to overcome these shortcomings, we implemented a simple and efficient spectral analysis, based on the fast Fourier transformation (FFT) approach, in order to evaluate the epidemic dynamic of scarlet fever incidence in China. This method was shown to generate more valid, meaningful and even simpler explanations than time- and frequency-domain analyses, especially for periodic variations caused by biological, physical, or environmental phenomena [Reference Peyton20].
We modelled data on the surveillance incidence of scarlet fever in China from 2004 to 2010. Scarlet fever is caused by erythrogenic toxin released by Streptococcus pyogenes. Nowadays, although scarlet fever is rare and generally mild, serious sequelae which threaten the heart and kidneys can still occur, especially in school children [Reference Lamden21, Reference Barnett and Frieden22]. The surveillance database of scarlet fever, together with the established knowledge of the cyclical behaviour of the infection, makes this disease an ideal example for studying epidemic dynamics using a FFT approach. Furthermore, we also include examples to show that this method can be easily applied to achieving various goals such as prediction and influencing factor exploration.
MATERIALS AND METHODS
Scarlet fever and environmental data
As prescribed by the Law of the P.R. China on the Prevention and Treatment of Infectious Diseases, physicians who find pathogen carriers or patients suspected of scarlet fever infection must report their findings to the local health and anti-epidemic agency within a specified time limit, next the health administration department under the State Council will promptly release information on and publicly announce the true epidemic situation. The original incidence data was obtained from the National Infectious Diseases Reporting System, Centers for Disease Prevention and Control, China. The incidence observations (represented by cases per100 000) to be analysed were aggregated by month from January 2004 to December 2010, for the whole nation and each region of mainland China (22 provinces, five autonomous regions, four municipalities, excluding Hong Kong, Macao SAR and Taiwan province). Moreover, we also excluded Jiangxi (code = 36) and Hainan (code = 46) provinces because there were too many zeros in the corresponding incidence time-series. Thus, there were 30 incidence time-series (each had 84 observations) analysed in our study. In addition, the environmental data (i.e. monthly sunshine hours, average relative humidity, average temperature and precipitation for major cities) were collected from the National Bureau of Statistics of China [23].
All statistical analyses and graphs in this paper were performed in R (R Foundation, Austria) which is a free software environment for statistical computing and graphics.
Methods of analysis
We denote X(t) as the number of scarlet fever incidences observed at time t. Based on the classical decomposition in time-series analysis [Reference Box and Jenkins5], incidence series {X(t)} are assumed to be represented as realization of the process:
In equation (1), the trend component, describing the long-term changes in data, is the polynomial function of time t. The periodic component is referred to as a function with known period, and the random noise component represents random errors, which is commonly treated as Gaussian white noise [Reference Sumi and Kamo15].
In the spectral analysis, the trend component can be easily obtained via maximum-likelihood estimation or least squares estimation; hence, the key point for analysis lies in the estimation of the periodic component. This component is described by the function X PC (t), which is assumed to be a mixture of cosine or sine functions with multiple frequencies and amplitudes.
where f
i
(=1/T
i; T
i is the period) is the frequency, A
0 is a constant indicating the average value of the periodic component, N is the total number of components, A
i
is the amplitude and
![]() $\phi _i $
the phase that determines the starting point of the cosine function. All A
0, A
i
, f
i
and
$\phi _i $
the phase that determines the starting point of the cosine function. All A
0, A
i
, f
i
and
![]() $\phi _i $
(i = 1, …, N) are parameters to be estimated in the model. In addition, through the derivative calculations in equation (2), we can obtain the maximum value and maximum point, t
max (at which the maximum value is reached), which respectively indicates the underlying peak and peak time in terms of epidemiology.
$\phi _i $
(i = 1, …, N) are parameters to be estimated in the model. In addition, through the derivative calculations in equation (2), we can obtain the maximum value and maximum point, t
max (at which the maximum value is reached), which respectively indicates the underlying peak and peak time in terms of epidemiology.
Although many spectral analysis methods take the form of equation (1) [Reference Sumi and Kamo15, Reference Alonso24], there are diverse estimations for parameters as stated in the previous section. Instead of being either too empirical or complicated, we aimed to establish the model simply with the help of FFT [Reference Cochran25]. As a consequence, our method involves the following two steps.
Step I. Data pre-processing
Time-series were rearranged from the original dataset by month for each region. Outliers were detected by hypothesis tests beforehand [Reference Tsay26–Reference Chang, Tiao and Chen28]. Two types of outliers were taken into account: addictive outliers and level shifts. Usually an addictive outlier is caused by a recording error and a level shift may be the result of an outbreak or control. Thus, addictive outliers should be studied carefully to check whether there is any justification for smoothing or discarding them. If any level shifts exist, it is advisable to analyse the series by first breaking it into homogeneous segments at the corresponding time point. After outlier detection, the trend component is fitted by a polynomial function of time t and then removed. This procedure, subtracting the fitted function from the time-series, is also known as detrending. It is recommended that the order of the estimated polynomial function for the trend component is determined by the shape of incidence curve and hypothesis test. Logarithmic transformation is performed for the detrended data if the frequency histogram is separate from the normal distribution required for spectral analysis.
Step II. FFT approach
This step is the core of our method. We take {X * t } to represent the pre-processed data after the first step. The concept of spectral analysis expresses the underlying dynamics in terms of periodic variations as Fourier frequencies being driven by sines and cosines. In this sense, FFT is employed as an efficient approach which transforms the data from the time domain (which can be considered as the function of time) into the frequency domain (i.e. the function of frequency):
where j/N is designated the Fourier or fundamental frequency. Since i in equation (3) is the imaginary unit denoted as i 2 = −1, the result of FFT is a complex number. Given the Fourier frequency, the FFT value can be calculated by equation (3). It is also guaranteed mathematically that the phase can be calculated through the arc-tangent function of the FFT value while the amplitude equals its module [Reference Bracewell29]. Thus, the amplitude-frequency curve and phase-frequency curve can be plotted. From the former curve the prominent frequencies, which correspond to the highest amplitudes, are identified, and from the latter curve the corresponding phases can then be estimated. Thus, the parameters in equation (2) can be estimated by FFT. The algorithms above are available in the STATS package of R software.
Furthermore, in order to take into account the variability of the parameters and the autocorrelation within time-series, the block bootstrap technique and permutation test were adopted [Reference Davision and Hinkley30]. The corresponding period of Fourier frequency (i.e. 1/Fourier frequency) was chosen to be the block length so that the autocorrelation structure within seasonal blocks is preserved. First, we simulated 10 000 replications under the null hypothesis of absence of seasonality by block bootstrap sampling, and then obtained the P value by comparing the initially observed statistics (peak or peak time) with the distribution of the 10 000 simulated replications. In addition, the confidence intervals of parameters were obtained with the bootstrap percentile method (level of significance = 0·05).
The two steps above constitute the main body of our method. If continuous periodic oscillations are identifiable, then our method should be able to predict and explain the cycling behaviour in terms of extrinsic or intrinsic factors [Reference Breban31]. However, in effect, these explorations may belong to the spectral analysis itself by definition, although they can be viewed as the derivatives of our approach.
RESULTS
Our analyses focused both on incidence data in each region and the general situation over the whole country. For clarity of interpretation, the raw incidence data for the whole nation, presented in Figure 1 a, is used as an illustration.
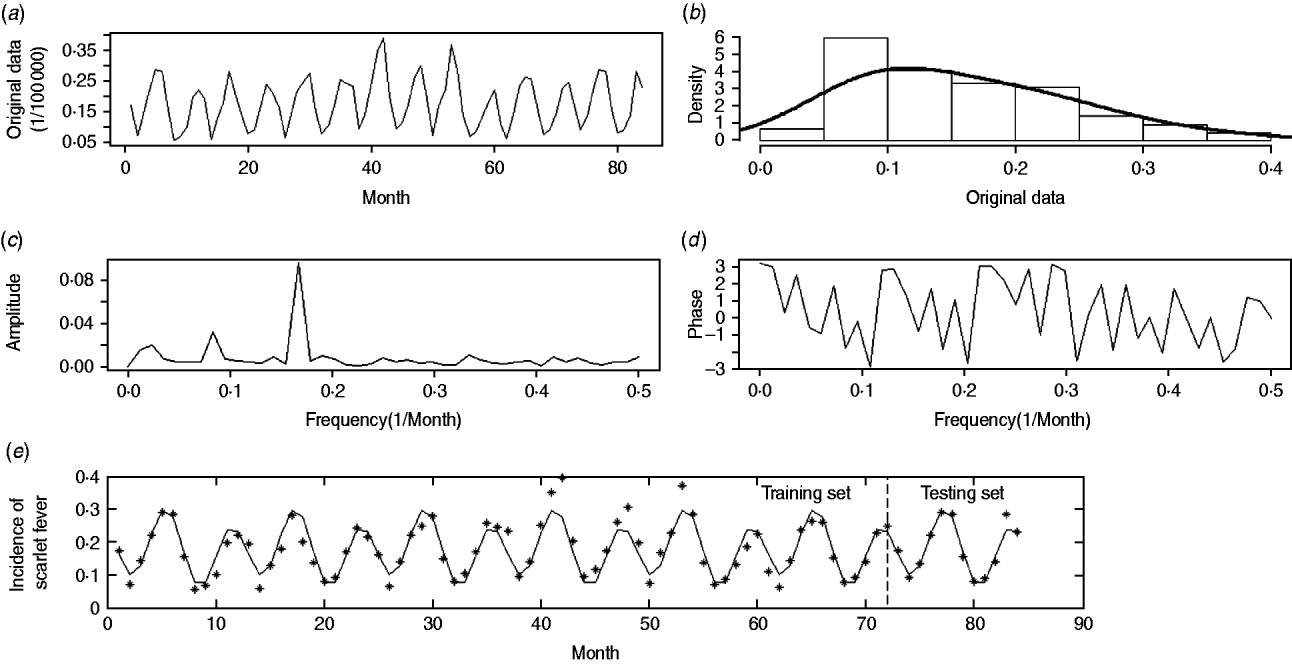
Fig. 1. Monthly incidence data of scarlet fever in China from 2004 to 2010. (a) The original time-series; (b) histogram of original area; (c) estimated amplitude-frequency curve; (d) estimated phase-frequency curve; (e) original data and fast-Fourier-transform forecast-fitted curve, with a vertical line splitting the training and testing periods.
Main results of the method
Step I
The national incidence series consisted of 84 observations and no outlier was detected (P > 0·05). As shown in Figure 1 a no sign of trend component was observed, and neither the linear (P = 0·54) nor quadratic (P = 0·70) regression curve of incidence on time was statistically significant. Figure 1 b shows that the frequency histogram of the national incidence data reasonably resembles the normal distribution with P = 0·07 from the Kolmogorov–Smirnov test, suggesting that the data are suitable for a FFT approach. Otherwise, logarithmic transformation is recommended before analysis.
Step II
We used FFT to further characterize the periodic component of the pre-processed data. Similarly to a triangular prism which decomposes the light into different frequencies in the colour spectrum, the FFT approach offers a straightforward means to isolate the periodic components oscillating at various frequencies. As mentioned above, we used the amplitude-frequency curve (Fig. 1 c) to identify the prominent frequency and subsequently determined the phase through the phase-frequency curve (Fig. 1 d).
In addition, we used a suitable bandpass filter [Reference Peyton20], which is a mode of constraining those frequencies within a certain range (e.g. 0·01⩽f⩽0·50) and rejecting frequencies outside that range, to reconstruct the periodic component in equation (1). Such an approach is reasonable because periods that are either too long or too short are considered inappropriate for the FFT approach. In Figure 1 c, the seasonality of scarlet fever in China was identified by an annual pattern (frequency = 0·0833, period ≈12 months) and a semi-annual pattern (frequency = 0·1667, period ≈6 months), respectively. As a result, the periodic component was able to be expressed in the following equation, where all the parameters were statistically significant (permutation tests, P < 0·05):
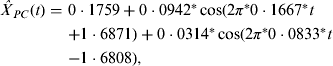 $$\hskip-2pt\eqalign{\hat X_{PC} (t) = \ & 0\cdot1759 + 0\cdot0942^*\cos ( {2\pi^*0\cdot1667^*t }\cr & {+ 1\cdot6871} ) + 0\cdot0314^*\cos ( {2\pi^*0\cdot0833^*t }\cr & {- 1\cdot6808} ),} $$
$$\hskip-2pt\eqalign{\hat X_{PC} (t) = \ & 0\cdot1759 + 0\cdot0942^*\cos ( {2\pi^*0\cdot1667^*t }\cr & {+ 1\cdot6871} ) + 0\cdot0314^*\cos ( {2\pi^*0\cdot0833^*t }\cr & {- 1\cdot6808} ),} $$
Finally, as there was no significant trend component in the data, the estimation for model (1) of the national situation could be expressed in a model with a single component as:
Based on equation (5), with parameter estimates as in equation (4), it can be concluded, by maximization and block bootstrapping, that the first peak occurred between March and April (peak time 1 = 4·02, 95% CI 3·88–4·81 months) with a peak value 0·19, while the second peak occurred between October and December (peak time 2 = 11·31, 95% CI 10·80–12·39 months).
Evaluation and application of the method
Prediction and validation
One of the most important applications of time-series analysis is prediction. The extrapolation of the epidemic curve fitted by equation (4) can be used for prediction of the incidence because it is regarded as the predictable part. For each incidence time-series, we split the data into the training set (January 2004–December 2009) and testing set (January 2010–December 2010), and used the first set for model fitting and the second set for making predictions.
To confirm the agreement between these two sets, we first calculated the mean values of training and testing sets separately for each incidence time-series, and then applied the Bland–Altman plot (see Fig. 2). In Figure 2, each incidence time-series is represented by assigning the average of the two mean values as the abscissa (x axis) value, and the difference between the two values as the ordinate (y axis) value. It can be seen from Figure 2 that despite just a few exceptions (i.e. Beijing, Liaoning, Heilongjiang), the training and testing sets are nearly identical within each incidence time-series. This was also verified by the paired two-sample t test (t = 0·6477, P = 0·5198).
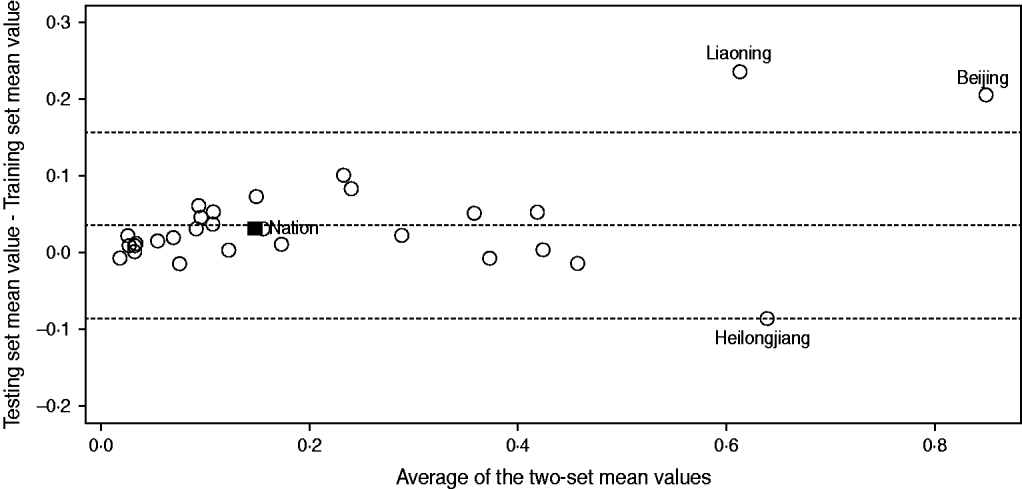
Fig. 2. Bland–Altman plot for the training and testing set mean values. The open symbols (○) represent the region-specific incidence time-series and the solid symbol (■) represents the national incidence time-series. The top and bottom dashed horizontal lines represent the 95% limits of agreement for each comparison, and the central dashed line represents the average of the difference between the two-set mean values.
Most of these series exhibit seasonal nonlinearity variation structure, so it seems plausible to introduce spectral analysis rather than a time-domain approach. To confirm this, we performed two analyses. First, we compared the internal and external validities of our method with those of the SARIMA model of time-domain approach. To take into account the relatively low incidence, we chose the mean absolute deviation (MAD) [Reference Goh and Law32] as an error measure. Table 1 lists the results of the whole nation as well as each region. As can be seen, even in the presence of outliers, the application of FFT takes on a lower MAD than the SARIMA model both for the in-sample and external sample errors in most cases.
Table 1. Comparison of errors for FFT spectral analysis and the SARIMA model*
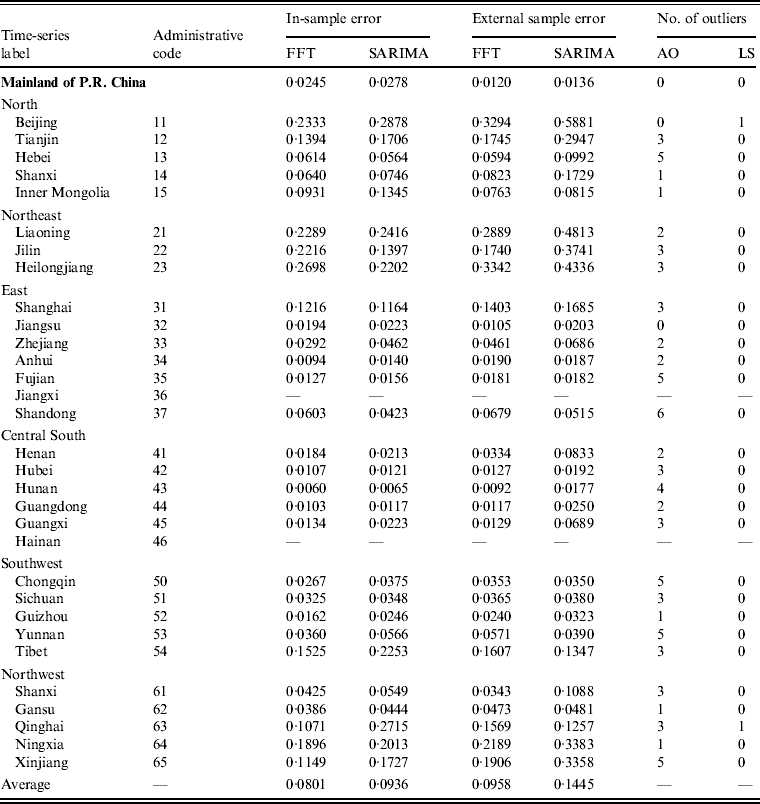
FFT, Fast Fourier transformation; SARIMA, seasonal autoregressive integrated moving average; AO, addictive outlier; LS, level shift.
* Mean absolute deviation is calculated as an error measure.
Second, we compared the average in-sample error and average out-of-sample error by each method. The values were 0·08 and 0·09, resprectively, for FFT (error difference ≈ 0·01), while the values were 0·09 and 0·14, respectively, for the SARIMA model (error difference ≈ 0·05). The larger error difference for the SARIMA model may be caused by over-fitting [Reference Box and Jenkins5]. Thus, the results for FFT appear to show a better performance than the SARIMA model.
Influencing factor exploration
Table 2 presents peaks and peak times extracted from each region (province, autonomous region, municipality). We found that both the first and second peaks were significantly large for the region-specific time-series. To examine whether latitude/longitude by region had an impact on the peaks and peak times, we further employed univariate regression models with the LSF method in which the peaks and peak times derived from each series were separate dependent variables, and the latitude/longitude with respect to each province were capital independent variables. It was found that the relationship between first/second peak and latitude was significant (first peak: R 2 = 0·6077, P < 0·001; second peak: R 2 = 0·5936, P < 0·001), while others were not. Figure 3(a, b) shows the plots of first/second peak values against the latitudes of province capitals. It is intriguing to find that the peak values (both first and second peaks) varied significantly along a latitudinal gradient. Namely, the peak values were highest in the northern zones while becoming attenuated southwards.

Fig. 3. Trends of peak variations in scarlet fever incidence by latitude across China. (a) The first peak against the latitude of regions; (b) the second peak against the latitude of regions. Each combination of symbols (triangle, square, circle) and colour (black for south, white for north) of the graph refers to the location of the corresponding region, while the size of the graph is proportional to the population of each region.
Table 2. Seasonal patterns of scarlet fever incidence time-series in P.R. China by region, 2004–2011*
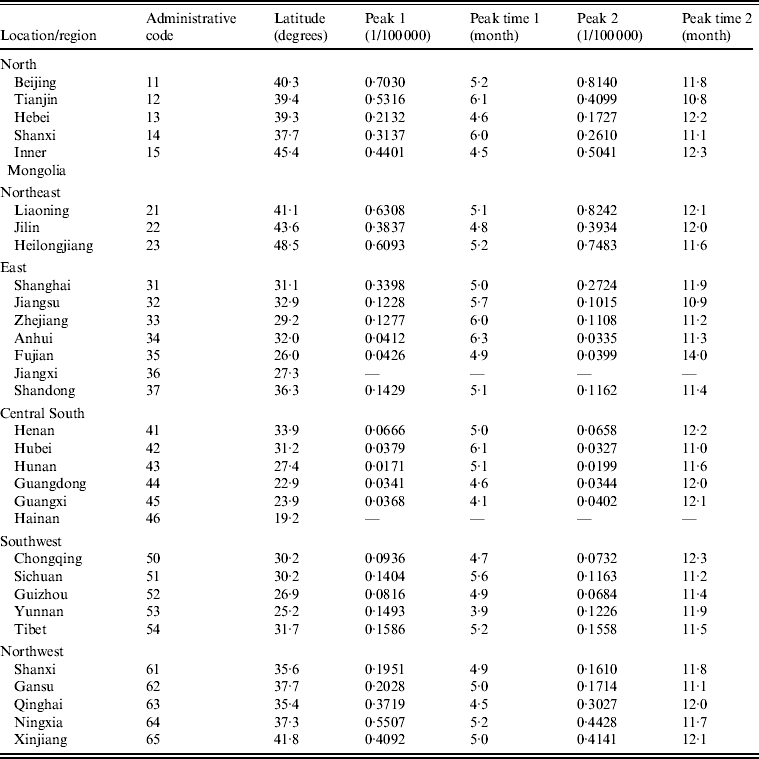
* The focus is on the mainland of the P.R. China, which does not contain Hong Kong, Macao SAR and Taiwan. Also excluded in analysis are Jiangxi (code = 36) and Hainan (code = 46) provinces because there are too many zeros in the corresponding time-series. The first digit of administrative code refers to the location: 1, North; 2, Northeast; 3, East; 4, Central South; 5, Southwest; 6, Northwest.
The geographical pattern in China as discussed above, has also been stated to be correlated with a variety of environmental factors (e.g. sunshine hours, precipitation, relative humidity, temperature) in previous studies [Reference Wang33, Reference Li34]. To confirm this, Pearson's product-moment correlation analysis was used. We found that the peak values were significantly positively correlated with sunshine hours (r = 0·23, P < 0·01), and negatively correlated with precipitation (r = −0·21, P < 0·01), relative humidity (r = −0·33, P < 0·01), and temperature (r = −0·23, P < 0·01). These results provided a clue for further investigation.
DISCUSSION
In this paper, we suggest that the regularity in time-series can be expressed in terms of periodic variations of the underlying phenomenon that produce the series, expressed as Fourier frequency driven by sines and cosines. We present a rather simple and efficient spectral analysis approach that has a tendency to outperform SARIMA models in both model-fitting and prediction.
In the previous section, we took the incidence data of the whole nation as an example. Such series may become an ideal paradigm since there is neither trend component nor outlier. However, other situations can be more complicated. For example, we detected a level shift change at t = 55 (July 2008) in the incidence series of Beijing. This is in accord with other studies, suggesting that the incidence of scarlet fever had fallen in Beijing prior to the 2008 Olympic Games [Reference Qian35]. Thus, we split the data at t = 55 and removed the trend term from each segment separately. As the detrended data were skewed, logarithmic transformation was then performed. After these adjustments, we applied spectral analysis to derive the periodic component; the results are shown in Table 1.
When comparing FFT and the SARIMA model, only five (16·7%) of the total of 30 series had a larger FFT in-sample error than the SARIMA model. As inferred by the larger number of outliers, the corresponding regions (i.e. Hebei, Liaoning, Heilongjiang, Shanghai, Shandong) are typically hotspots for scarlet fever outbreaks in China [Reference Liu, Wang and Wang36]. There are four regions (i.e. Shandong, Tibet, Qinghai, Yunnan) where the external sample error for FFT is obviously greater than it is for the SARIMA model. By checking the original data, we found that scarlet fever incidence in these regions changed from 20% to 50% in 2010 compared to the incidence over the last 6 years while the national average level remained unchanged. These results imply that, on the one hand, changes in data structure can have unavoidable influences on spectral analysis. However, by contrast, empirical evidence with FFT showing many more minimal errors and lower error difference seems to affirm the validity and robustness of spectral analysis compared to that of the time-domain approach.
China is the world's third largest country, extending about 50 degrees of latitude, encompassing diverse regional climates, terrain, population densities and social customs, etc. The application of the results of our method suggest that environmental forces (precipitation, relative humidity, temperature) play an important role in scarlet fever epidemics in China, which coincides with epidemics reported in previous studies in the Czech Republic and Russia, as well as some cities in China [Reference Wang33, Reference Li34, Reference Briko37, Reference Hubalek38]. The application sheds light on the underlying practical value of our method. Since spectral analysis can provide different perspectives compared to conventional time-series models, it is reasonable to expect more applications of the method in future investigations on scarlet fever and other infectious diseases to be performed.
Time-series analysis is a data-driven technique. To our knowledge, epidemics of streptococcal infection including scarlet fever, as well as other diseases such as chickenpox, are fundamentally determined by the mechanism of the noisy limit cycle [Reference Olsen and Schaffer9], which leads to the temporal changes shown as seasonal variations. Therefore, we believe that, under appropriate conditions (e.g. normality and absence of outliers) of data structure, our procedure will contribute to further studies of many other periodically oscillating diseases. More studies on transmission dynamics are still required.
ACKNOWLEDGEMENTS
The authors thank the anonymous referees for their constructive comments on the manuscript. We are extremely grateful to Dr Liu Yuanyuan (Sichuan University, China) for inspiring discussions and valuable advice. Our thanks are also due to Katrina Seymour (University of Technology, Sydney) and Dr Bao Huanchen (University of Virginia) for revision of the paper. This study was supported by the National Natural Science Foundation (grant no. 30571618) and National Special Foundation for Health Research (grant no. 200802133) of China.
DECLARATION OF INTEREST
None.









