INTRODUCTION
The main route of transmission of the hepatitis C virus (HCV) in developed countries is through injection drug use, which accounts for up to 80% of infections in England and Wales [Reference De Angelis1]. Overall it is estimated that HCV prevalence is about 50% in England, although in other European Union countries national prevalence of HCV infection in injecting drug users (IDUs) ranges from 12% to >75% [2]. There is also likely to be great variation of HCV prevalence within individual countries as well as between them. In the UK, serosurveillance studies suggest a substantial regional variation [Reference Sweeting3] with a greater than threefold difference in HCV prevalence between individual sites, e.g. from 60% in Manchester to <20% in North East England and South Wales [Reference Craine4, Reference Hickman5]. Similar variations have been reported within other countries, e.g. in Italy prevalence in IDUs ranges from 31% to 87% [2]. Clearly, the risk of HCV infection can be very different between areas (with estimates of HCV incidence in IDUs in the UK ranging from <5/100 person-years to 40/100 person-years [Reference Craine4, Reference Judd6, Reference Hope7]), and therefore opportunities for prevention and scale of the intervention coverage required to reduce transmission also vary [Reference Martin8, Reference Vickerman, Hickman and Judd9].
IDUs are a difficult to reach population, partially covered and represented by a mixture of data sources (such as data from needle exchanges, specialist drug treatment, prisons) [Reference Hickman10]. Information on HCV prevalence in IDUs is not available through routine laboratory surveillance of diagnostic tests, because reporting of exposure categories is incomplete or missing and because not all those at risk come forward for testing. Public health surveillance of HCV infection, therefore, often relies upon sentinel and other surveys of IDUs that purposively recruit through community services and settings [Reference Hope11]. In England, the unlinked anonymous monitoring survey (UAM) of IDUs [12, 13] monitors the prevalence of antibodies to HCV (anti-HCV) and HIV (anti-HIV) in those attending a national sample of specialist services for drug users in about one-third of 149 local Drug Action Teams (DATs) responsible for commissioning services in England. It is impractical and too costly to undertake such surveys in every local area. Further, some of the samples are too small to provide direct estimates of local area anti-HCV prevalence in the sampled areas as the survey's focus is on producing national data [13]. Statistical models are therefore required to use the available data from the survey and other auxiliary sources to derive local estimates.
Synthetic estimation, which uses simple regression models of prevalence in terms of chosen auxiliary variables in the sampled areas, is commonly applied in situations such as these to obtain estimates in areas that have not been sampled [Reference Ghangurde and Singh14–Reference Bajekal16]. However, this approach assumes a relationship between the outcome and the auxiliary (predictor) variables that may be incorrect, relatively weak and subject to systematic (e.g. spatial) variation; and does not correctly account for uncertainty in the estimated regression coefficients. Random-effects models [Reference Bajekal16, Reference Rao17] are often used to reduce the uncertainty of estimates by borrowing strength via shrinkage, but do not account for the uncertainty of estimates in the non-sampled areas, which reduce to the simple synthetic estimator where the random effect is assumed to be zero.
Instead, we propose to overcome this problem by assuming that neighbouring areas tend to be more similar than distant ones, i.e. there is spatial correlation. The inclusion of spatially correlated random effects then allows the estimation of random effects in non-sampled areas, also incorporating an appropriate degree of uncertainty in the prevalence estimate (A. Saei & R. Chambers, University of Southampton, unpublished data). In this paper we propose models of this form for the estimation of local HCV prevalence in recent IDUs in contact with services in England, extending them to a Bayesian framework as described by Gómez-Rubio (N. Gómez Rubio, S. Best, et al., unpublished data) and, for example, Best et al. [Reference Best, Richardson and Thomson18].
MATERIALS AND METHODS
Data sources
The principal data source used is the UAM survey of IDUs, which samples from harm reduction and treatment services in selected DATs, these being chosen to give a broad range of geographical and urban/rural settings. Respondents voluntarily and anonymously provide an oral fluid sample for testing [Reference Judd19], and complete a brief questionnaire. The survey received multi-centre ethics committee approval. In the analyses here only those that have injected in the last year are considered (termed ‘recent injectors’). Data are in the form of a numerator and denominator for participants from each DAT area, year, age group and sex combination; with age split into three age groups: 15–29, 30–44 and 45–59 years, and for the years 2006–2008 (Table 1).
Table 1. Summary of data on recent injectors from the National Drug Treatment Monitoring System (NDTMS) in 2008 and unlinked anonymous monitoring (UAM) survey of injecting drug users, England, 2006–2008 aggregated
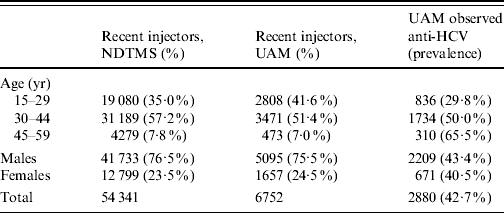
Anti-HCV, Antibodies to hepatitis C virus.
Auxiliary information on crime, uptake of benefits, population density and age structure, deprivation and health is available from the Office of National Statistics [20] (ONS) at the Local Authority District (LAD) level. ONS data in terms of counts or numbers were summed to DAT-level totals if the DAT covered more than one LAD. Per-person rates or proportions for each DAT were calculated using ONS estimates of population size [21], and log rates (or logit of proportions) were used as covariates in analyses to aid the prediction of prevalence estimates.
The final data source is the National Drug Treatment Monitoring System [22] (NDTMS) which collects data on drug users receiving addiction treatment. This is used to relate prevalence estimates from the UAM data to the treated population, under the assumption that those in treatment are representative of those in contact with all services. These data consist of numbers of recent injectors (within the last year) in treatment by age and sex for each DAT (Table 1).
HCV prevalence model
Observed HCV prevalence ![]() for DAT d, year t, age a and sex s was modelled via logistic regression, similar to that described by Besag et al. [Reference Besag, York and Mollie23], with the following basic form:
for DAT d, year t, age a and sex s was modelled via logistic regression, similar to that described by Besag et al. [Reference Besag, York and Mollie23], with the following basic form:
where αa,s is an age-sex specific intercept, βt is the effect of year, and βpop.i (i=1, 2,7 …, n) are population-level effects from auxiliary ONS data (e.g. log rate of drug offences). The component v d is an unstructured random effect at the DAT level, distributed independently as ![]() if the area is ever sampled in 2006–2008 and zero otherwise. The u d are conditionally autoregressive terms for the spatially correlated random effects at the DAT level. These are conditional on the group of surrounding neighbours (not including d), u -d, with the form
if the area is ever sampled in 2006–2008 and zero otherwise. The u d are conditionally autoregressive terms for the spatially correlated random effects at the DAT level. These are conditional on the group of surrounding neighbours (not including d), u -d, with the form
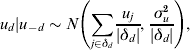
where δd is the group of contiguous neighbours that share a boundary with area d and |δd| the number of neighbours, and the sum of the random effects u d is constrained to equal zero. Deviation from the prevalence estimated by auxiliary information is therefore shared between the unstructured and spatially correlated random effects: the stronger the spatial correlation, the more variation being explained by the u d.
The oral fluid test for antibodies to HCV (anti-HCV) has a sensitivity of 91·7% and a specificity of 99·2% [Reference Judd19]. The observed prevalence ![]() is related to the true prevalence p d,t,a,s as described in Sweeting et al. [Reference Sweeting3].
is related to the true prevalence p d,t,a,s as described in Sweeting et al. [Reference Sweeting3].
Overall DAT-level prevalence for DAT d in year t, p d,t, is expressed as a weighted average of the prevalence estimates described above, p d,t,a,s, with weighting according to the age-sex distribution of recent injectors in treatment from the NDTMS data, i.e.:
where N d,t,a,s is the number of recent injectors in DAT d, year t, age a and sex s. This weighting relates estimates from the UAM survey data to the population of recent injectors in treatment, correcting for any over- or under-sampling of demographic groups in the UAM survey data.
Estimation of ![]() in equation (1) is performed in a Bayesian framework, requiring specification of prior distributions for each parameter. A uniform prior is placed on standard deviations of unstructured and spatial random effects (σv and σu), this form being shown to have good properties for hierarchical models [Reference Gelman24]. Inverse gamma priors on variances were also investigated to test robustness under different assumptions. All regression parameters and intercept terms in the logistic model were given flat prior distributions (priors with equal probability on the entire real line).
in equation (1) is performed in a Bayesian framework, requiring specification of prior distributions for each parameter. A uniform prior is placed on standard deviations of unstructured and spatial random effects (σv and σu), this form being shown to have good properties for hierarchical models [Reference Gelman24]. Inverse gamma priors on variances were also investigated to test robustness under different assumptions. All regression parameters and intercept terms in the logistic model were given flat prior distributions (priors with equal probability on the entire real line).
Posterior distributions were obtained via Markov Chain-Monte Carlo techniques implemented in WinBUGS [Reference Spiegelhalter25]. Medians and 95% credible intervals (CrIs) were on the basis of 50 000 iterations from two chains running in parallel, following a 5000 iteration ‘burn-in’ period. Convergence was assessed through the use of the Brooks–Gelman diagnostic [Reference Brooks and Gelman26].
Model comparison
Various potential covariates and alternative model formulations were investigated, with further details shown in the Results section. Models were compared via the deviance information criterion [Reference Spiegelhalter, Best and Carlin27] (DIC), a measure of model fit plus a penalty for model complexity, which can be expressed as ![]() , where
, where ![]() is the posterior mean deviance and p D is the effective number of parameters in the model. We also assessed the predictive performance of models via leave one out cross-validation (CV) [Reference Van Houwelingen and le Cessie28–Reference May30], where data for each of the k sampled DATs are omitted in turn and the model is estimated based on data from the k–1 remaining DATs. Measures of discrepancy can then be calculated using observed and predicted values for the omitted DAT, such as the deviance, which can then be summed across all DATs to provide a summary statistic for the model being tested. Given that the data have a binomial distribution, the CV deviance takes the form
is the posterior mean deviance and p D is the effective number of parameters in the model. We also assessed the predictive performance of models via leave one out cross-validation (CV) [Reference Van Houwelingen and le Cessie28–Reference May30], where data for each of the k sampled DATs are omitted in turn and the model is estimated based on data from the k–1 remaining DATs. Measures of discrepancy can then be calculated using observed and predicted values for the omitted DAT, such as the deviance, which can then be summed across all DATs to provide a summary statistic for the model being tested. Given that the data have a binomial distribution, the CV deviance takes the form
where devCV is the sum of CV deviances, p d(−d) is HCV prevalence estimated in DAT d with data for DAT d omitted, and r d and n d the observed numerator and denominator in DAT d. For clarity, the summation over year, age and sex is not shown in the above equation. Use of equation (4) is intended to provide an assessment of out-of-sample predictive performance, which is a primary goal of the model due to the large number of non-sampled DATs for which estimates are required, and we chose models that minimize devCV and therefore provide the closest values to ‘unseen’ data.
RESULTS
Data from 6752 recent injectors participating in the UAM survey during 2006–2008 were used in the analyses. Of these, two-fifths (41·6%) were aged 15–29, and a quarter (24·5%) were female (Table 1). Female participants tended to be younger than males with 51·2% aged 15–29 years compared to 38·4% of males. Overall, 2880 (42·7%) tested positive for HCV antibodies.
Of the 149 DATs, 52 were sampled during 2006–2008. The median sample size taken from each DAT in 2008 was 32, with interquartile range 23–64, and a range from 2 to 206. The small sample size in some of the DATs reflects recruitment only through treatment services where most of those participating were ex-injectors (i.e. had not injected in the last year). Of the nine government office regions, the best represented was the South East, with 10/19 (53%) DATs sampled, while in Yorkshire and the Humber only 1/15 (7%) was sampled. Other regions ranged from 29% to 42% of DATs being sampled.
Model choice
Results comparing different auxiliary covariates are shown in Table 2. The model including logit proportion of adults aged <35 years (proportion <35) gave the best DIC and CV deviance scores, although many covariate choices had a similar DIC score. It is interesting to note that some variables, such as sex offences, gave reasonable DIC scores but poor predictive performance. This can be explained by the increase in σv, as the random effects give a smooth fit for sampled DATs but do not aid in the prediction of non-sampled DATs, for which v reduces to zero. Choosing ‘proportion <35’ as the principal auxiliary variable, we found that the inclusion of further covariates did not improve the model, with the exception of drug offences. These two covariates were therefore used in subsequent models.
Table 2. Comparison statistics for models of prevalence of antibodies to hepatitis C virus in injecting drug users, England, 2006–2008

![]() , Posterior mean deviance; p D, effective number of model parameters; DIC, deviance information criteria (
, Posterior mean deviance; p D, effective number of model parameters; DIC, deviance information criteria (![]() ); CV, cross-validation deviance (measure of predictive performance); OR, odds ratio per standard deviation increase of covariate; σv, σu, standard deviations of unstructured (v) and spatially correlated random effects (u).
); CV, cross-validation deviance (measure of predictive performance); OR, odds ratio per standard deviation increase of covariate; σv, σu, standard deviations of unstructured (v) and spatially correlated random effects (u).
Results comparing alternative model formulations, with the omission and extension of various components, are shown in Table 3. The use of spatially correlated random effects (u) greatly improves predictive ability and hence CV deviance increases if this is omitted, although as mentioned above, the unstructured effects (v) take up the remaining variation if this is omitted and this does not translate to a great difference in DIC. The converse was true with the omission of v: DIC is significantly worse, but there is actually a small improvement in CV deviance. With the omission of both, model fit is worse by both measures; although CV deviance is better than the v only model, with the covariate for drug offences having a stronger effect.
Table 3. Comparison statistics for alternative models of prevalence of antibodies to hepatitis C virus in injecting drug users, England, 2006–2008

![]() , Posterior mean deviance; p D, effective number of model parameters; DIC, deviance information criteria (
, Posterior mean deviance; p D, effective number of model parameters; DIC, deviance information criteria (![]() ); CV, cross-validation deviance (measure of predictive performance); OR, odds ratio per standard deviation increase of covariate; σv, σ u, standard deviations of unstructured (v) and spatially correlated random effects (u).
); CV, cross-validation deviance (measure of predictive performance); OR, odds ratio per standard deviation increase of covariate; σv, σ u, standard deviations of unstructured (v) and spatially correlated random effects (u).
Models use proportion of adults aged <35 years and drug crime as covariates. Where components vary over time, values for years 2006, 2007 and 2008 are shown in order.
In terms of extending the model, DIC scores were worse with the addition of further complexity. CV deviance improved a little when allowing separate v terms for each year, but this may exaggerate spatial effects and over-fit to the sampled areas – the time-varying σv are far smaller and there may be identification problems. We therefore retained the basic form of the model; results for model parameters are shown in Table 4.
Table 4. Final model for prevalence of antibodies to hepatitis C virus in injecting drug users, England, 2006–2008, posterior medians and 95% credible intervals

CrI, Credible interval.
We compared model results using alternative priors for variance components, testing Gamma(0·5, 0·005) priors, as recommended by Kelsall & Wakefield [Reference Kelsall, Wakefield, Bernado, Berger and Dawid31], and flat Gamma(0·1, 0·1) priors. Results were similar with the Gamma(0·1, 0·1) prior (σv=0·351, σu=0·697) but the large probability mass near zero for the Gamma(0·5, 0·005) prior reduced the more weakly identified unstructured random effects, with the spatial effects becoming more pronounced to compensate (σv=0·150, σu=0·801). Prevalence estimates were similar for all choices.
HCV prevalence estimates
Anti-HCV prevalence estimates ranged from 14% to 82%, with a median of 43% and interquartile range from 32% to 54%. In contrast, observed prevalence ranged from 5% to 77%. Model estimates are more homogeneous due to shrinkage, and slightly higher as they account for the imperfect sensitivity of the test. A forest plot of anti-HCV prevalence estimates and credible intervals for each DAT in 2008 are displayed in Figure 1; and shaded maps of prevalence can be seen in Appendix 1 (available online). Prevalence is generally low in the North East and South West, with high prevalence DATs in and around central London, the North West, and a number of towns and cities (Brighton, Bristol, Leeds, Nottingham, Reading, Portsmouth).

Fig. 1. Prevalence of antibodies to hepatitis C virus in injecting drug users in contact with specialist drug services, England, 2008. Posterior medians and credible intervals for each Drug Action Team (DAT) are displayed by region. Ever-sampled DATs (during 2006–2008) are shown with solid diamonds, non-sampled DATs with hollow diamonds.
To examine the effects of model components, the spatially correlated effect u, unstructured random effect v, and effects of the auxiliary variables are plotted as shaded maps (see Appendix 1, online). The spatial effects exhibit two broad areas of increased prevalence (beyond that predicted by auxiliary covariates): in the North West, and in London and the areas to its south east; with a broad band of lower prevalence diagonally across the rest of the country. The auxiliary variable for ‘proportion <35’ has a stronger effect than drug offences, although patterns differ in some areas, with ‘proportion <35’ increasing odds of HCV in most large cities, but the variable for drug offences predominantly affecting London and the North West areas. (For full listings of DAT-level model effects see Appendix 2, available online.)
DISCUSSION
Main findings
We have shown that there is substantial local variation in anti-HCV prevalence, with areas of high prevalence concentrated in London, the North West, parts of the South East and some major cities. We found a relationship between the proportion of young adults in the adult population and anti-HCV prevalence, although other predictors produced similar patterns of results, which were generally insensitive to model choice. A spatial effect was well-identified in the model, indicating that areas tend to be influenced by their neighbours, beyond what may be predicted from the covariates and demographic variables included in the model.
Strengths and limitations
This work aimed to provide the best possible local-level estimates of anti-HCV prevalence in recent IDUs in contact with specialist services for drug users across England. This goal was hampered by sparse data, which we sought to overcome by using auxiliary information that exhibits a link with anti-HCV prevalence, and by taking advantage of spatial patterns. Despite these efforts, uncertainty remains in prevalence estimates for non-sampled areas, particularly in areas with unusual covariate levels and contrasting or imprecise spatial effects. As long as this uncertainty at the DAT level is considered we believe that these estimates are a reliable indication of the general patterns in the anti-HCV prevalence in recent IDUs across England.
The DAT-level prevalence estimates are weighted according to the demographic distribution of all recent injectors undergoing treatment for their drug use, and are derived using data obtained from the sample of specialist services collaborating in the UAM survey. However, the UAM survey recruits from both harm reduction services (such as needle exchanges) and drug treatment services (such as substitute prescribing programmes and structured counselling) while only clients of the latter types of service are included in the NDTMS data. The NDTMS data describes those in treatment well; however, it is assumed here that it is generally representative of the characteristics of recent IDUs in contact with all specialist services. This assumption is supported by the fact that three-quarters of the recent IDUs participating in the UAM survey reporting needle-exchange use also reported currently receiving substitute drug treatment (data not shown), while others would be in structured counselling which is not enquired of in the survey. Of course, these DAT-level estimates still do not necessarily reflect prevalence in all recent IDUs as they do not include those not in contact with specialist services. However, the use of specialist services by IDUs in England is very extensive, with considerable overlap in injectors recruited from community and treatment and any differences in HCV prevalence largely due to differences in age or injecting duration [Reference Hickman5].
As far as we are aware, the assessment of spatial models when there are non-sampled areas has not been investigated. We argue that the use of ‘leave one out’ cross-validation provides the best assessment of predictive ability in this setting. The DIC may not be informative for assessing out-of-sample prediction, as variation that is not explained by covariate effects may be taken up by either unstructured or spatially structured random effects, although models that make use of spatial correlation will provide better out-of-sample prediction. Posterior predictive model checks have been suggested as an alternative to full cross-validation [Reference Marshall and Spiegelhalter32], but these methods are principally concerned with model fit, and further investigation is required to assess their application when the goal is out-of-sample prediction.
Out estimates are based partly on auxiliary data, chosen primarily on the basis of model selection. However, these predictors also have plausible interpretations: the proportion of the adult population aged <35 years may be viewed as a measure of urbanicity; and drug crime may act as a proxy for severity of problem drug use. Taken together these factors are surmised to give an indication of which environments are more likely to experience high levels of HCV infection. Prevalence estimates for non-sampled areas may be sensitive to model choice, and we therefore assessed the robustness of prevalence estimates to the use of different auxiliary variables. Estimates were similar for most alternatives, although including only drug offences as a covariate decreased the prevalence estimates for 10 DATs by 5–8% and increased those for City of London and Isle of Wight by 18% and 17%, respectively. This is due to high rates of drug offences relative to the proportion of adults aged <35 years in these areas.
Findings in relation to the evidence base
The substantial geographical variation in anti-HCV prevalence observed here is consistent with previous studies, but allows a more formal assessment of this phenomenon via a modelling process that provides for the first time prevalence estimates for all local areas. For some DATs HCV prevalence has been estimated using respondent driven sampling (RDS) [Reference Heckathorn33], which is postulated to be the most reliable way to obtain representative estimates for hidden populations [Reference Malekinejad34]; however, only IDUs that have injected in the last 4 weeks were included. Results are available for Bristol [Reference Hickman35], Birmingham and Leeds (M. Hickman, V. Hope, personal communication), showing a prevalence of 57% (95% CI 52–62), 38% (95% CI 33–44) and 58% (95% CI 53–64), respectively, compared to 60% (95% CrI 50–70), 44% (95% CrI 25–61) and 51% (95% CrI 26–76) in this study. Our results are uncertain for the non-sampled areas (Birmingham, Leeds), and the RDS method does necessarily generate unbiased estimates [Reference Goel and Salganik36] so no firm conclusions may be drawn, although the results appear to follow a broadly similar pattern for the areas covered. Previously, estimates have only been available at a regional level for England, and have not used the NDTMS data to relate findings to a wider population. These data thus complement regional and national data, as well as strengthening local evidence.
Implications
The estimates of anti-HCV prevalence for non-sampled areas have substantial uncertainty and need to be viewed with some caution; however, they will provide DATs with a more robust indication of the HCV prevalence in recent IDUs in contact with specialist services than relying on regional estimates of prevalence. This is especially so for those regions, like the East Midlands, with very marked variations in prevalence at the DAT level. These estimates therefore have public health utility as they permit more informed local commissioning of services to prevent, diagnose and treat HCV infection in this population group. As these estimates use routinely available data they can be repeated over time; doing this would allow the monitoring of local trends in anti-HCV prevalence in IDUs, and so permit service commissioning to adapt to these.
CONCLUSIONS
The novel approach adopted here has produced local estimates of anti-HCV prevalence of use in informing local public health responses. The limitations to these estimates need to be noted and the methods employed need further validation and refinement. However, there is potential to apply these methods to other issues affecting IDUs, such as hepatitis B infection or even behavioural data, e.g. needle and syringe sharing or the uptake of diagnostic testing. This approach may also be of use in other situations where data are sparse and local-level estimates are needed to inform response; e.g. sexual health indicators in men who have sex with men and sex workers or general health issues in marginalized groups such as the homeless.
NOTE
Supplementary material accompanies this paper on the Journal's website (http://journals.cambridge.org/hyg).
ACKNOWLEDGMENTS
The authors thank Dr Stefano Conti and Dr Ayoub Saei for their comments and advice; Karl Molden for the provision of National Drug Treatment Monitoring System data; and all the collaborators involved with the unlinked anonymous prevalence monitoring programme, as well as the drug users who gave their time to be interviewed.
This work was supported by the United Kingdom Department of Health (grant number GHP 003/002/024).
DECLARATION OF INTEREST
None.









