Hostname: page-component-7479d7b7d-68ccn Total loading time: 0 Render date: 2024-07-11T14:21:52.388Z Has data issue: false hasContentIssue false
  • English
  • Français

WEAK CONVERGENCE TO DERIVATIVES OF FRACTIONAL BROWNIAN MOTION

Published online by Cambridge University Press:  05 December 2022

Søren Johansen Open the ORCID record for Søren Johansen [Opens in a new window]  and
Morten Ørregaard Nielsen Open the ORCID record for Morten Ørregaard Nielsen [Opens in a new window]
Søren Johansen
Affiliation:
University of Copenhagen and CREATES
Morten Ørregaard Nielsen*
Affiliation:
Aarhus University
*
Address correspondence to Morten Ørregaard Nielsen, Department of Economics and Business Economics, Aarhus University, Aarhus, Denmark; e-mail: mon@econ.au.dk.
Get access Rights & Permissions [Opens in a new window]

Abstract

It is well known that, under suitable regularity conditions, the normalized fractional process with fractional parameter d converges weakly to fractional Brownian motion (fBm) for 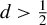$d>\frac {1}{2}$ . We show that, for any nonnegative integer M, derivatives of order 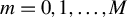$m=0,1,\dots ,M$ of the normalized fractional process with respect to the fractional parameter d jointly converge weakly to the corresponding derivatives of fBm. As an illustration, we apply the results to the asymptotic distribution of the score vectors in the multifractional vector autoregressive model.

Type
ARTICLES
Information
Econometric Theory , First View , pp. 1 - 16
Copyright
© The Author(s), 2022. Published by Cambridge University Press.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

We are grateful to the Editor (Peter C.B. Phillips) and two anonymous referees for very helpful and detailed comments. We thank the Danish National Research Foundation for financial support (DNRF Chair Grant No. DNRF154).

References

REFERENCES

Abramowitz, M. & Stegun, I.A. (1972) Handbook of Mathematical Functions . National Bureau of Standards.Google Scholar
Akonom, J. & Gourieroux, C. (1987) A functional central limit theorem for fractional processes. Technical report 8801, CEPREMAP, Paris.Google Scholar
Billingsley, P. (1968) Convergence of Probability Measures . Wiley.Google Scholar
Davydov, Y.A. (1970) The invariance principle for stationary processes. Theory of Probability and its Applications 15, 487–498.10.1137/1115050CrossRefGoogle Scholar
Einmahl, U. (1989) Extensions of results of Komlós, Major, and Tusnády to the multivariate case. Journal of Multivariate Analysis 28, 20–68.CrossRefGoogle Scholar
Franchi, M. (2010) A representation theory for polynomial cofractionality in vector autoregressive models. Econometric Theory 26, 1201–1217.10.1017/S0266466609990508CrossRefGoogle Scholar
Hualde, J. (2012) Weak convergence to a modified fractional Brownian motion. Journal of Time Series Analysis 33, 519–529.CrossRefGoogle Scholar
Hualde, J. (2014) Estimation of long-run parameters in unbalanced cointegration. Journal of Econometrics 178, 761–778.CrossRefGoogle Scholar
Johansen, S. (2008) A representation theory for a class of vector autoregressive models for fractional processes. Econometric Theory 24, 651–676.CrossRefGoogle Scholar
Johansen, S. & Nielsen, M.Ø. (2012a) A necessary moment condition for the fractional functional central limit theorem. Econometric Theory 28, 671–679.CrossRefGoogle Scholar
Johansen, S. & Nielsen, M.Ø. (2012b) Likelihood inference for a fractionally cointegrated vector autoregressive model. Econometrica 80, 2667–2732.Google Scholar
Johansen, S. & Nielsen, M.Ø. (2016) The role of initial values in conditional sum-of-squares estimation of nonstationary fractional time series models. Econometric Theory 32, 1095–1139.CrossRefGoogle Scholar
Johansen, S. & Nielsen, M.Ø. (2021) Statistical inference in the multifractional cointegrated VAR model. Aarhus University, in preparation.Google Scholar
Marinucci, D. & Robinson, P.M. (1999) Alternative forms of fractional Brownian motion. Journal of Statistical Planning and Inference 80, 111–122.10.1016/S0378-3758(98)00245-6CrossRefGoogle Scholar
Marinucci, D. & Robinson, P.M. (2000) Weak convergence of multivariate fractional processes. Stochastic Processes and their Applications 86, 103–120.CrossRefGoogle Scholar
Roman, S. (1980) The formula of Faà di Bruno. American Mathematical Monthly 87, 805–809.10.1080/00029890.1980.11995156CrossRefGoogle Scholar
Taqqu, M.S. (1975) Weak convergence to fractional Brownian motion and to the Rosenblatt process. Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete 31, 287–302.CrossRefGoogle Scholar