Article contents
UNIFORM ASYMPTOTIC NORMALITY IN STATIONARY AND UNIT ROOT AUTOREGRESSION
Published online by Cambridge University Press: 14 April 2011
Abstract
While differencing transformations can eliminate nonstationarity, they typically reduce signal strength and correspondingly reduce rates of convergence in unit root autoregressions. The present paper shows that aggregating moment conditions that are formulated in differences provides an orderly mechanism for preserving information and signal strength in autoregressions with some very desirable properties. In first order autoregression, a partially aggregated estimator based on moment conditions in differences is shown to have a limiting normal distribution that holds uniformly in the autoregressive coefficient ρ, including stationary and unit root cases. The rate of convergence is 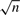 when
when 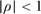 and the limit distribution is the same as the Gaussian maximum likelihood estimator (MLE), but when ρ = 1 the rate of convergence to the normal distribution is within a slowly varying factor of n. A fully aggregated estimator (FAE) is shown to have the same limit behavior in the stationary case and to have nonstandard limit distributions in unit root and near integrated cases, which reduce both the bias and the variance of the MLE. This result shows that it is possible to improve on the asymptotic behavior of the MLE without using an artificial shrinkage technique or otherwise accelerating convergence at unity at the cost of performance in the neighborhood of unity. Confidence intervals constructed from the FAE using local asymptotic theory around unity also lead to improvements over the MLE.
and the limit distribution is the same as the Gaussian maximum likelihood estimator (MLE), but when ρ = 1 the rate of convergence to the normal distribution is within a slowly varying factor of n. A fully aggregated estimator (FAE) is shown to have the same limit behavior in the stationary case and to have nonstandard limit distributions in unit root and near integrated cases, which reduce both the bias and the variance of the MLE. This result shows that it is possible to improve on the asymptotic behavior of the MLE without using an artificial shrinkage technique or otherwise accelerating convergence at unity at the cost of performance in the neighborhood of unity. Confidence intervals constructed from the FAE using local asymptotic theory around unity also lead to improvements over the MLE.
- Type
- ARTICLES
- Information
- Copyright
- Copyright © Cambridge University Press 2011
References
REFERENCES
- 18
- Cited by




