Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Johnson, Paul
Pandharipande, Rahul
and
Tseng, Hsian-Hua
2011.
Abelian Hurwitz-Hodge integrals.
Michigan Mathematical Journal,
Vol. 60,
Issue. 1,
Pagani, Nicola
2012.
The Chen–Ruan cohomology of moduli of curves of genus 2 with marked points.
Advances in Mathematics,
Vol. 229,
Issue. 3,
p.
1643.
Pagani, N.
and
Tommasi, O.
2013.
The orbifold cohomology of moduli of genus 3 curves.
Manuscripta Mathematica,
Vol. 142,
Issue. 3-4,
p.
409.
Jockers, Hans
Kumar, Vijay
Lapan, Joshua M.
Morrison, David R.
and
Romo, Mauricio
2014.
Two-Sphere Partition Functions and Gromov–Witten Invariants.
Communications in Mathematical Physics,
Vol. 325,
Issue. 3,
p.
1139.
Coates, Tom
Corti, Alessio
Iritani, Hiroshi
and
Tseng, Hsian-Hua
2015.
A mirror theorem for toric stacks.
Compositio Mathematica,
Vol. 151,
Issue. 10,
p.
1878.
Ishii, Akira
and
Ueda, Kazushi
2015.
The special McKay correspondence and exceptional collections.
Tohoku Mathematical Journal,
Vol. 67,
Issue. 4,
Pagani, Nicola
2016.
Moduli of abelian covers of elliptic curves.
Journal of Pure and Applied Algebra,
Vol. 220,
Issue. 3,
p.
1258.
Bruzzo, Ugo
Pedrini, Mattia
Sala, Francesco
and
Szabo, Richard J.
2016.
Framed sheaves on root stacks and supersymmetric gauge theories on ALE spaces.
Advances in Mathematics,
Vol. 288,
Issue. ,
p.
1175.
Bergh, Daniel
Lunts, Valery A.
and
Schnürer, Olaf M.
2016.
Geometricity for derived categories of algebraic stacks.
Selecta Mathematica,
Vol. 22,
Issue. 4,
p.
2535.
Sala, Francesco
and
Schiffmann, Olivier
2019.
The circle quantum group and the infinite root stack of a curve.
Selecta Mathematica,
Vol. 25,
Issue. 5,




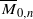 . We prove a closed formula for the total Chern class of
. We prove a closed formula for the total Chern class of 