Editorial
A letter from the Editors
-
- Published online by Cambridge University Press:
- 01 September 2010, p. 1113
-
- Article
-
- You have access
- Export citation
Research Article
Schemes over 𝔽1 and zeta functions
- Part of:
-
- Published online by Cambridge University Press:
- 21 April 2010, pp. 1383-1415
-
- Article
-
- You have access
- Export citation
K-theory Schubert calculus of the affine Grassmannian
- Part of:
-
- Published online by Cambridge University Press:
- 26 January 2010, pp. 811-852
-
- Article
-
- You have access
- Export citation
Spectral decomposition of compactly supported Poincaré series and existence of cusp forms
- Part of:
-
- Published online by Cambridge University Press:
- 22 January 2010, pp. 1-20
-
- Article
-
- You have access
- Export citation
Analytic continuation of overconvergent Hilbert eigenforms in the totally split case
- Part of:
-
- Published online by Cambridge University Press:
- 02 February 2010, pp. 541-560
-
- Article
-
- You have access
- Export citation
Zeros of systems of 𝔭-adic quadratic forms
- Part of:
-
- Published online by Cambridge University Press:
- 22 January 2010, pp. 271-287
-
- Article
-
- You have access
- Export citation
Regular and residual Eisenstein series and the automorphic cohomology of Sp(2,2)
- Part of:
-
- Published online by Cambridge University Press:
- 23 November 2009, pp. 21-57
-
- Article
-
- You have access
- Export citation
Rational points on cubic hypersurfaces that split off a form. With an appendix by J.-L. Colliot-Thélène
- Part of:
-
- Published online by Cambridge University Press:
- 15 February 2010, pp. 853-885
-
- Article
-
- You have access
- Export citation
Le lemme fondamental pondéré. I. Constructions géométriques
- Part of:
-
- Published online by Cambridge University Press:
- 19 May 2010, pp. 1416-1506
-
- Article
-
- You have access
- Export citation
Néron models and limits of Abel–Jacobi mappings
- Part of:
-
- Published online by Cambridge University Press:
- 02 February 2010, pp. 288-366
-
- Article
-
- You have access
- Export citation
The semisimplicity conjecture for A-motives
- Part of:
-
- Published online by Cambridge University Press:
- 18 March 2010, pp. 561-598
-
- Article
-
- You have access
- Export citation
Unitary dual of GL(n) at archimedean places and global Jacquet–Langlands correspondence
- Part of:
-
- Published online by Cambridge University Press:
- 08 June 2010, pp. 1115-1164
-
- Article
-
- You have access
- Export citation
On the minimal ramification problem for ℓ-groups
- Part of:
-
- Published online by Cambridge University Press:
- 18 March 2010, pp. 599-606
-
- Article
-
- You have access
- Export citation
Conjecture de monodromie-poids pour quelques variétés de Shimura unitaires
- Part of:
-
- Published online by Cambridge University Press:
- 26 January 2010, pp. 367-403
-
- Article
-
- You have access
- Export citation
On some modular representations of the Borel subgroup of GL2(Qp)
- Part of:
-
- Published online by Cambridge University Press:
- 11 December 2009, pp. 58-80
-
- Article
-
- You have access
- Export citation
K1 of products of Drinfeld modular curves and special values of L-functions
- Part of:
-
- Published online by Cambridge University Press:
- 08 June 2010, pp. 886-918
-
- Article
-
- You have access
- Export citation
The distribution of close conjugate algebraic numbers
- Part of:
-
- Published online by Cambridge University Press:
- 22 June 2010, pp. 1165-1179
-
- Article
-
- You have access
- Export citation
Local Fourier transform and epsilon factors
- Part of:
-
- Published online by Cambridge University Press:
- 05 August 2010, pp. 1507-1551
-
- Article
-
- You have access
- Export citation
Statistics of the zeros of zeta functions in families of hyperelliptic curves over a finite field
- Part of:
-
- Published online by Cambridge University Press:
- 11 December 2009, pp. 81-101
-
- Article
-
- You have access
- Export citation
On existence of log minimal models
- Part of:
-
- Published online by Cambridge University Press:
- 05 February 2010, pp. 919-928
-
- Article
-
- You have access
- Export citation

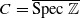 over 𝔽
over 𝔽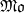 -schemes to interpret conceptually the spectral realization of zeros of
-schemes to interpret conceptually the spectral realization of zeros of 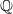 with no more than
with no more than 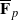 -representation
-representation 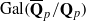 by using Fontaine’s theory of (φ,Γ)-modules. We compute Ω(
by using Fontaine’s theory of (φ,Γ)-modules. We compute Ω(