Article contents
On the Bateman–Horn conjecture for polynomials over large finite fields
Published online by Cambridge University Press: 21 September 2016
Abstract
We prove an analogue of the classical Bateman–Horn conjecture on prime values of polynomials for the ring of polynomials over a large finite field. Namely, given non-associate, irreducible, separable and monic (in the variable  $x$) polynomials
$x$) polynomials 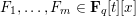 $F_{1},\ldots ,F_{m}\in \mathbf{F}_{q}[t][x]$, we show that the number of
$F_{1},\ldots ,F_{m}\in \mathbf{F}_{q}[t][x]$, we show that the number of 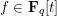 $f\in \mathbf{F}_{q}[t]$ of degree
$f\in \mathbf{F}_{q}[t]$ of degree 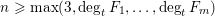 $n\geqslant \max (3,\deg _{t}F_{1},\ldots ,\deg _{t}F_{m})$ such that all
$n\geqslant \max (3,\deg _{t}F_{1},\ldots ,\deg _{t}F_{m})$ such that all 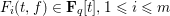 $F_{i}(t,f)\in \mathbf{F}_{q}[t],1\leqslant i\leqslant m$, are irreducible is
$F_{i}(t,f)\in \mathbf{F}_{q}[t],1\leqslant i\leqslant m$, are irreducible is 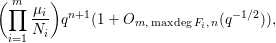 $$\begin{eqnarray}\displaystyle \biggl(\mathop{\prod }_{i=1}^{m}\frac{\unicode[STIX]{x1D707}_{i}}{N_{i}}\biggr)q^{n+1}(1+O_{m,\,\max \deg F_{i},\,n}(q^{-1/2})), & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \biggl(\mathop{\prod }_{i=1}^{m}\frac{\unicode[STIX]{x1D707}_{i}}{N_{i}}\biggr)q^{n+1}(1+O_{m,\,\max \deg F_{i},\,n}(q^{-1/2})), & & \displaystyle \nonumber\end{eqnarray}$$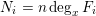 $N_{i}=n\deg _{x}F_{i}$ is the generic degree of
$N_{i}=n\deg _{x}F_{i}$ is the generic degree of 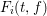 $F_{i}(t,f)$ for
$F_{i}(t,f)$ for 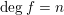 $\deg f=n$ and
$\deg f=n$ and 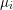 $\unicode[STIX]{x1D707}_{i}$ is the number of factors into which
$\unicode[STIX]{x1D707}_{i}$ is the number of factors into which  $F_{i}$ splits over
$F_{i}$ splits over 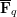 $\overline{\mathbf{F}}_{q}$. Our proof relies on the classification of finite simple groups. We will also prove the same result for non-associate, irreducible and separable (over
$\overline{\mathbf{F}}_{q}$. Our proof relies on the classification of finite simple groups. We will also prove the same result for non-associate, irreducible and separable (over 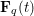 $\mathbf{F}_{q}(t)$) polynomials
$\mathbf{F}_{q}(t)$) polynomials 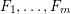 $F_{1},\ldots ,F_{m}$ not necessarily monic in
$F_{1},\ldots ,F_{m}$ not necessarily monic in  $x$ under the assumptions that
$x$ under the assumptions that  $n$ is greater than the number of geometric points of multiplicity greater than two on the (possibly reducible) affine plane curve
$n$ is greater than the number of geometric points of multiplicity greater than two on the (possibly reducible) affine plane curve 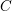 $C$ defined by the equation
$C$ defined by the equation 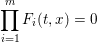 $$\begin{eqnarray}\displaystyle \mathop{\prod }_{i=1}^{m}F_{i}(t,x)=0 & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\prod }_{i=1}^{m}F_{i}(t,x)=0 & & \displaystyle \nonumber\end{eqnarray}$$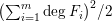 $(\sum _{i=1}^{m}\deg F_{i})^{2}/2$, where
$(\sum _{i=1}^{m}\deg F_{i})^{2}/2$, where 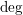 $\deg$ denotes the total degree in
$\deg$ denotes the total degree in 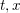 $t,x$) and
$t,x$) and 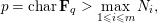 $$\begin{eqnarray}\displaystyle p=\text{char}\,\mathbf{F}_{q}>\max _{1\leqslant i\leqslant m}N_{i}, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle p=\text{char}\,\mathbf{F}_{q}>\max _{1\leqslant i\leqslant m}N_{i}, & & \displaystyle \nonumber\end{eqnarray}$$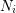 $N_{i}$ is the generic degree of
$N_{i}$ is the generic degree of 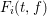 $F_{i}(t,f)$ for
$F_{i}(t,f)$ for 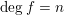 $\deg f=n$.
$\deg f=n$.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author 2016
References
- 5
- Cited by




