Hostname: page-component-77c89778f8-vsgnj Total loading time: 0 Render date: 2024-07-20T06:19:50.992Z Has data issue: false hasContentIssue false
  • English
  • Français

On 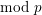$\text{mod}~p$ non-abelian Lubin–Tate theory for 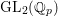$\text{GL}_{2}(\mathbb{Q}_{p})$

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  12 March 2015

Przemysław Chojecki
Przemysław Chojecki*
Affiliation:
Institut Mathématique de Jussieu, 4, place de Jussieu, 75252 Paris, France email chojecki@math.jussieu.fr University of Warsaw, Wydzial Matematyki, Informatyki i Mechaniki ul. Banacha 2, 02-097 Warsaw, Poland
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We analyse the 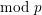$\text{mod}~p$ étale cohomology of the Lubin–Tate tower both with compact support and without support. We prove that there are no supersingular representations in the 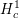$H_{c}^{1}$ of the Lubin–Tate tower. On the other hand, we show that in 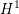$H^{1}$ of the Lubin–Tate tower appears the 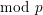$\text{mod}~p$ local Langlands correspondence and the 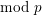$\text{mod}~p$ local Jacquet–Langlands correspondence, which we define in the text. We discuss the local-global compatibility part of the Buzzard–Diamond–Jarvis conjecture which appears naturally in this context.

Keywords

Galois representationsLanglands programLubin–Tate tower

MSC classification

Primary: 11F75: Cohomology of arithmetic groups 11F80: Galois representations 11F03: Modular and automorphic functions
Type
Research Article
Information
Compositio Mathematica , Volume 151 , Issue 8 , August 2015 , pp. 1433 - 1461
Copyright
© The Author 2015 

References

Berkovich, V., Étale cohomology for non-Archimedean analytic spaces, Publ. Math. Inst. Hautes Études Sci. 78 (1993), 5–161.CrossRefGoogle Scholar
Berkovich, V., Vanishing cycles for formal schemes I, Invent. Math. 115 (1994), 539–571.CrossRefGoogle Scholar
Berkovich, V., On the comparison theorem for étale cohomology of non-Archimedean analytic spaces, Israel J. Math. 92 (1995), 45–60.CrossRefGoogle Scholar
Berkovich, V., Étale equivariant sheaves on p-adic analytic spaces, Preprint (1995).Google Scholar
Berkovich, V., Vanishing cycles for formal schemes II, Invent. Math. 125 (1996), 367–390.CrossRefGoogle Scholar
Berger, L., La correspondence de Langlands locale p-adique pour GL2(ℚp), Astérisque 339 (2011), 157–180.Google Scholar
Berger, L., Central characters for smooth irreducible modular representations of GL 2(ℚp), Rend. Semin. Mat. Univ. Padova 128 (2012), 1–6.CrossRefGoogle Scholar
Boyer, P., Mauvaise reduction des varietes de Drinfeld et correspondance de Langlands locale, Invent. Math. 138 (1999), 573–629.CrossRefGoogle Scholar
Breuil, C., Sur quelques représentations modulaires et p-adiques de GL2(ℚp) I, Compositio Math. 138 (2003), 165–188.CrossRefGoogle Scholar
Breuil, C., Sur quelques représentations modulaires et p-adiques de GL2(ℚp) II, J. Inst. Math. Jussieu 2 (2003), 1–36.CrossRefGoogle Scholar
Breuil, C., Sur un probleme de compatibilite local-global modulo p pour GL2, J. Reine Angew. Math. 692 (2014), 1–76.CrossRefGoogle Scholar
Breuil, C. and Diamond, F., Formes modulaires de Hilbert modulo p et valeurs d’extensions galoisiennes, Ann. Sci. Éc. Norm. Supér. (4) 47 (2014), 905–974.CrossRefGoogle Scholar
Breuil, C. and Pas̆kūnas, V., Towards a modulo p Langlands correspondence for GL2, Mem. Amer. Math. Soc. 216 (2012).Google Scholar
Buzzard, K., Analytic continuation of overconvergent eigenforms, J. Amer. Math. Soc. 16 (2003), 29–55.CrossRefGoogle Scholar
Buzzard, K., Diamond, F. and Jarvis, F., On Serre’s conjecture for mod l Galois representations over totally real fields, Duke Math. J. 55 (2010), 105–161.Google Scholar
Buzzard, K. and Gee, T., Explicit reduction modulo p of certain 2-dimensional crystalline representations II, Bull. Lond. Math. Soc. 45 (2013), 779–788.CrossRefGoogle Scholar
Calegari, F. and Emerton, M., Completed cohomology — a survey, Nonabelian fundamental groups and Iwasawa theory (Cambridge University Press, Cambridge), to appear.Google Scholar
Carayol, H., Sur les representations l-adiques associees aux formes modulaires de Hilbert, Ann. Sci. Éc. Norm. Supér. (4) 19 (1986), 409–468.CrossRefGoogle Scholar
Casselman, W., On some results of Atkin and Lehner, Math. Ann. 201 (1973), 301–314.CrossRefGoogle Scholar
Chojecki, P., On non-abelian Lubin–Tate theory and analytic cohomology, Preprint (2014) arXiv:1402.5606.Google Scholar
Colmez, P., Representations de GL2(ℚp) et (𝜑, Γ)-modules, Astérisque 330 (2010), 281–509.Google Scholar
Coleman, R., On the components of X 0(p n), J. Number Theory 110 (2005), 3–21.CrossRefGoogle Scholar
Dat, J.-F., Espaces symetriques de Drinfeld et correspondance de Langlands locale, Ann. Sci. Éc. Norm. Supér. (4) 39 (2006), 1–74.CrossRefGoogle Scholar
Dat, J.-F., Theorie de Lubin–Tate non-abelienne l-entiere, Duke Math. J. 161 (2012), 951–1010.CrossRefGoogle Scholar
Deligne, P., letter to Piatetski-Shapiro (1973).Google Scholar
Emerton, M., On the interpolation of systems of Hecke eigenvalues, Invent. Math. 164 (2006), 1–84.CrossRefGoogle Scholar
Emerton, M., Ordinary parts of admissible representations of p-adic reductive groups I. Definition and first properties, Astérisque 331 (2010), 335–381.Google Scholar
Emerton, M., Local-global compatibility in the $p$-adic Langlands programme for $\text{GL}_{2}(\mathbb{Q})$, Preprint (2011), available at http://math.uchicago.edu/∼emerton/preprints.html.Google Scholar
Emerton, M. and Helm, D., The local Langlands correspondence for GLn  in families, Ann. Sci. Éc. Norm. Supér. (4) to appear, arXiv:1104.0321.Google Scholar
Emerton, M., Gee, T. and Herzig, F., Weight cycling and Serre-type conjectures for unitary groups, Preprint (2011).Google Scholar
Emerton, M. and Pas̆kūnas, V., On effaceability of certain 𝛿-functors, Astérisque 331 (2010), 439–447.Google Scholar
Fargues, L., Cohomologie des espaces de modules de groupes p-divisibles et correspondances de Langlands locales, Astérisque 291 (2004), 1–200.Google Scholar
Fargues, L., L’isomorphisme entres les tours de Lubin–Tate et de Drinfeld et applications cohomologiques, in L’isomorphisme entre les tours de Lubin–Tate et de Drinfeld, Progress in Mathematics, vol. 262 (Birkhäuser, 2008).CrossRefGoogle Scholar
Gee, T. and Savitt, D., Serre weights for quaternion algebras, Compositio Math. 147 (2011), 1059–1086.CrossRefGoogle Scholar
Haines, T. and Rapoport, M., Shimura varieties with Γ1(p)-level via Hecke algebra isomorphisms: The Drinfeld case, Ann. Sci. Éc. Norm. Supér. (4) 45 (2012), 719–785.CrossRefGoogle Scholar
Harris, M. and Taylor, R., The geometry and cohomology of some simple Shimura varieties, Annals of Mathematics Studies, vol. 151 (Princeton University Press, Princeton, NJ, 2001).Google Scholar
Helm, D., On the modified mod $p$local Langlands correspondence for $\text{GL}_{2}(\mathbb{Q}_{l})$, Preprint (2012), available at http://wwwf.imperial.ac.uk/∼dhelm/.CrossRefGoogle Scholar
Huber, R., Étale cohomology of rigid analytic varieties and adic spaces, Aspects of Mathematics, vol. 30 (Vieweg, Braunschweig, 1996).CrossRefGoogle Scholar
Katz, N. and Mazur, B., Arithmetic moduli of elliptic curves, Annals of Mathematics Studies, vol. 108 (Princeton University Press, Princeton, NJ, 1985).CrossRefGoogle Scholar
Khare, C., A local analysis of congruences in the (p, p) case: Part II, Invent. Math. 143 (2001), 129–155.CrossRefGoogle Scholar
Khare, C., Serre’s modularity conjecture: the level one case, Duke Math. J. 134 (2006), 557–589.CrossRefGoogle Scholar
Pas̆kūnas, V., Coefficient systems and supersingular representations of GL 2(F), Mém. Soc. Math. Fr. (N.S.) 99 (2004).Google Scholar
Pas̆kūnas, V., On the restriction of representations of GL 2(F) to a Borel subgroup, Compositio Math. 143 (2007), 1533–1544.CrossRefGoogle Scholar
Pas̆kūnas, V., Extensions for supersingular representations of GL 2(ℚp), Astérisque 331 (2010), 297–333.Google Scholar
Pas̆kūnas, V., Blocks for mod $p$representations of $GL_{2}(\mathbb{Q}_{p})$, Preprint (2011), arXiv:1104.5602.Google Scholar
Pas̆kūnas, V., On the image of Colmez’s Montreal functor, Publ. Math. Inst. Hautes Études Sci. 118 (2013), 1–191.CrossRefGoogle Scholar
Pink, R., Arithmetical compactification of mixed Shimura varieties, Bonner Math. Schriften, vol. 209 (Fachbibliothek Mathematik, Bonn, 1990).Google Scholar
Serre, J.-P., Two letters on quaternions and modular forms (mod p), Israel J. Math. 95 (1996), 281–299.CrossRefGoogle Scholar
Shin, S.W., Supercuspidal part of the mod l cohomology of GU(1,n-1)-Shimura varieties, J. Reine Angew. Math., to appear, available at http://math.mit.edu/∼swshin/.CrossRefGoogle Scholar
Strauch, M., Geometrically connected components of deformation spaces of one-dimensional formal modules, Pure Appl. Math. Q. 4 (2008), 1–18.CrossRefGoogle Scholar
Vignéras, M.-F., Representations modulaires galois-quaternions pour un corps p-adique, in Journees Arithmétiques d’Ulm, Lecture Notes in Mathematics, vol. 1380 (Springer, 1989), 254–266.Google Scholar
Vignéras, M.-F., Representations modulaires GL (2, F) en caracteristique l, F corps p-adique, p≠l, Compositio Math. 72 (1989), 33–66.Google Scholar
Vignéras, M.-F., Representations modulo p of the p-adic group GL (2, F), Compositio Math. 140 (2004), 333–358.CrossRefGoogle Scholar
Yoshida, T., On non-abelian Lubin–Tate theory via vanishing cycles, in Algebraic and arithmetic structures of moduli spaces (Sapporo 2007), Advanced Studies in Pure Mathematics, vol. 58 (Mathematical Society of Japan, 2010), 361–402.CrossRefGoogle Scholar