Article contents
Lower bounds for Maass forms on semisimple groups
Published online by Cambridge University Press: 17 April 2020
Abstract
Let 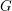 $G$ be an anisotropic semisimple group over a totally real number field
$G$ be an anisotropic semisimple group over a totally real number field 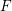 $F$. Suppose that
$F$. Suppose that  $G$ is compact at all but one infinite place
$G$ is compact at all but one infinite place 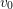 $v_{0}$. In addition, suppose that
$v_{0}$. In addition, suppose that 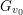 $G_{v_{0}}$ is
$G_{v_{0}}$ is 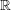 $\mathbb{R}$-almost simple, not split, and has a Cartan involution defined over
$\mathbb{R}$-almost simple, not split, and has a Cartan involution defined over 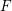 $F$. If
$F$. If 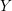 $Y$ is a congruence arithmetic manifold of non-positive curvature associated with
$Y$ is a congruence arithmetic manifold of non-positive curvature associated with 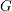 $G$, we prove that there exists a sequence of Laplace eigenfunctions on
$G$, we prove that there exists a sequence of Laplace eigenfunctions on 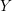 $Y$ whose sup norms grow like a power of the eigenvalue.
$Y$ whose sup norms grow like a power of the eigenvalue.
- Type
- Research Article
- Information
- Copyright
- © The Authors 2020
Footnotes
FB is supported by ANR grant 14-CE25 and SM is supported by NSF grant DMS-1902173.
References
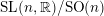 $\text{SL}(n,\mathbb{R})/\text{SO}(n)$, Preprint (2015), arXiv:1505.07285.Google Scholar
$\text{SL}(n,\mathbb{R})/\text{SO}(n)$, Preprint (2015), arXiv:1505.07285.Google Scholar- 4
- Cited by




