Hostname: page-component-76fb5796d-x4r87 Total loading time: 0 Render date: 2024-04-26T20:11:04.632Z Has data issue: false hasContentIssue false
  • English
  • Français

Density of potentially crystalline representations of fixed weight

Part of: Discontinuous groups and automorphic forms Algebraic number theory: local and $p$-adic fields

Published online by Cambridge University Press:  23 May 2016

Eugen Hellmann  and
Benjamin Schraen
Eugen Hellmann
Affiliation:
Mathematisches Institut, Universität Bonn, Endenicher Allee 60, 53115 Bonn, Germany email hellmann@math.uni-bonn.de
Benjamin Schraen
Affiliation:
Centre de Mathematique Laurent Schwartz, École Polytechnique, 91128 Palaiseau Cedex, France email benjamin.schraen@polytechnique.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 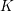$K$ be a finite extension of 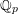$\mathbb{Q}_{p}$ and let 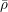$\bar{\unicode[STIX]{x1D70C}}$ be a continuous, absolutely irreducible representation of its absolute Galois group with values in a finite field of characteristic 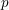$p$. We prove that the Galois representations that become crystalline of a fixed regular weight after an abelian extension are Zariski-dense in the generic fiber of the universal deformation ring of 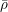$\bar{\unicode[STIX]{x1D70C}}$. In fact we deduce this from a similar density result for the space of trianguline representations. This uses an embedding of eigenvarieties for unitary groups into the spaces of trianguline representations as well as the corresponding density claim for eigenvarieties as a global input.

Keywords

p-adic Hodge theory(𝜑, 𝛤)-modulesdeformations of Galois representations

MSC classification

Primary: 11S20: Galois theory
Secondary: 11F85: $p$-adic theory, local fields 11F80: Galois representations
Type
Research Article
Information
Compositio Mathematica , Volume 152 , Issue 8 , August 2016 , pp. 1609 - 1647
Copyright
© The Authors 2016 

References

Bellaiche, J. and Chenevier, G., Families of Galois representations and Selmer groups , Astérisque 324 (2009).Google Scholar
Berger, L. and Colmez, P., Familles de représentations de de Rham et monodromie p-adique , Astérisque 319 (2008), 303–337.Google Scholar
Breuil, C., Hellmann, E. and Schraen, B., Une interprétation modulaire de la variété trianguline, Preprint (2014), arXiv:1411.7260.Google Scholar
Bushnell, C. and Henniart, G., The local Langlands conjecture for GL(2) (Springer, Berlin, 2006).CrossRefGoogle Scholar
Bushnell, C. and Kutzko, P., Semisimple Types in GL n , Compositio Math. 119 (1999), 53–97.Google Scholar
Buzzard, K., Eigenvarieties , in L-functions and Galois representations, 59–120, London Mathematical Society Lecture Note Series, vol. 320 (Cambridge University Press, Cambridge, 2007).Google Scholar
Chenevier, G., Une application des varietes de Hecke des groupes unitaires, available at http://gaetan.chenevier.perso.math.cnrs.fr/pub.html.Google Scholar
Chenevier, G., Sur la densité des représentations cristallines du groupe de Galois absolu de ℚ p , Math. Ann. 335 (2013), 1469–1525.CrossRefGoogle Scholar
Chenevier, G., The p-adic analytic space of pseudocharacters of a profinite group, and pseudorepresentations over arbitrary rings, in Automorphic forms and Galois representations, London Mathematical Society Lecture Note Series, vol. 414 (Cambridge University Press, Cambridge, 2014).CrossRefGoogle Scholar
Clozel, L., Représentations galoisiennes associées aux représentations automorphes autoduales de GL(n) , Publ. Math. Inst. Hautes Études Sci. 73 (1991), 97–145.Google Scholar
Colmez, P., Représentations triangulines de dimension 2 , Astérisque 319 (2008), 213–258.Google Scholar
Conrad, B., Relative ampleness in rigid geometry , Ann. Inst. Fourier (Grenoble) 56 (2006), 1049–1126.Google Scholar
de Jong, A., Crystalline Dieudonné module theory via formal and rigid geometry , Publ. Math. Inst. Hautes Études Sci. 82 (1995), 5–96.Google Scholar
Emerton, M. and Gee, T., A geometric perspective on the Breuil-Mézard Conjecture , J. Inst. Math. Jussieu 13 (2014), 183–223.Google Scholar
Fontaine, J.-M., Représentations p-adiques semi-stables , Astérisque 223 (1994), 113–184.Google Scholar
Fontaine, J.-M., Représentations ℓ-adiques potentiellement semi-stables , Astérisque 223 (1994), 321–347.Google Scholar
Grothendieck, A., Éléments de géométrie algébrique : IV. Étude locale des schémas et des morphismes de schémas , Publ. Mat. Inst. Hautes Études Sci. 20 (1964), 5–259.Google Scholar
Gee, T. and Kisin, M., The Breuil-Mézard conjecture for potentially Barsotti–Tate representations , Forum Math. Pi 2 (2014), e1.Google Scholar
Hellmann, E., Families of $p$ -adic Galois representations and $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$ -modules, Preprint (2012), arXiv:1202.3413.Google Scholar
Hellmann, E., Families of trianguline representations and finite slope spaces, Preprint (2012), arXiv:1202.4408.Google Scholar
Huber, R., A generalization of formal schemes and rigid analytic varieties , Math. Z. 217 (1994), 513–551.CrossRefGoogle Scholar
Huber, R., Étale cohomology of rigid analytic varieties and adic spaces, Aspects of Mathematics, vol. 30 (Springer, Wiesbaden).Google Scholar
Kedlaya, K. and Liu, R., On families of (𝜑, 𝛤)-modules , Algebra Number Theory 4 (2010), 943–967.Google Scholar
Kedlaya, K., Pottharst, J. and Xiao, L., Cohomology of arithmetic families of (𝜑, 𝛤)-modules , J. Amer. Math. Soc. 27 (2014), 1043–1115.Google Scholar
Kisin, M., Potentially semi-stable deformation rings , J. Amer. Math. Soc. 21 (2008), 513–546.Google Scholar
Kisin, M., Moduli of finite flat group schemes, and modularity , Ann. of Math. (2) 107 (2009), 1085–1180.Google Scholar
Kisin, M., Deformations of  Gℚ p and GL2(ℚ p ) representations , Astérisque 330 (2010), 511–528.Google Scholar
Köpf, U., Über eigentliche Familien algebraischer Varietäten über affinoiden Räumen , Schr. Math. Inst. Univ. Münster 2(Heft 7) (1974), iv+72 pp.Google Scholar
Liu, R., Triangulation of refined families , Comment. Math. Helv. 90 (2015), 831–904.Google Scholar
Loeffler, D., Overconvergent algebraic automorphic forms , Proc. Lond. Math. Soc. (3) 102 (2011), 193–228.Google Scholar
Nakamura, K., Classification of two dimensional split trianguline representations of p-adic fields , Compositio Math. 145 (2009), 865–914.Google Scholar
Nakamura, K., Deformations of trianguline B-pairs and Zariski density of two dimensional crystalline representations, Preprint (2010), arXiv:1006.4891.Google Scholar
Nakamura, K., Zariski density of crystalline representations for any p-adic field, Preprint (2011), arXiv:1104.1760.Google Scholar
Pappas, G. and Rapoport, M., 𝛷-modules and coefficient spaces , Mosc. Math. J. 9 (2009), 625–664.Google Scholar
Raynaud, M., Anneaux Locaux Henséliens, Lecture Notes in Mathematics 169 (Springer, Berlin, 1970).CrossRefGoogle Scholar
Thorne, J., On the automorphy of ℓ-adic representations with small residual image , J. Inst. Math. Jussieu 11 (2012), 855–920.Google Scholar
van der Put, M. and Schneider, P., Points and topologies in rigid geometry , Math. Ann. 302 (1995), 81–103.Google Scholar