Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Khan, Rizwanur
2016.
THE DIVISOR FUNCTION IN ARITHMETIC PROGRESSIONS MODULO PRIME POWERS.
Mathematika,
Vol. 62,
Issue. 3,
p.
898.
Khan, Rizwanur
Milićević, Djordje
and
Ngo, Hieu T.
2016.
Non-Vanishing of DirichletL-Functions in Galois Orbits.
International Mathematics Research Notices,
p.
rnv320.
Irving, Alastair James
2016.
Estimates for Character Sums and DirichletL-Functions to Smooth Moduli.
International Mathematics Research Notices,
Vol. 2016,
Issue. 15,
p.
4602.
Saha, Abhishek
2017.
Hybrid sup-norm bounds for Maass newforms of powerful level.
Algebra & Number Theory,
Vol. 11,
Issue. 5,
p.
1009.
Munshi, Ritabrata
2018.
Geometry, Algebra, Number Theory, and Their Information Technology Applications.
Vol. 251,
Issue. ,
p.
273.
Munshi, Ritabrata
and
Singh, Saurabh Kumar
2019.
Weyl bound for p-power twist of GL(2)L-functions.
Algebra & Number Theory,
Vol. 13,
Issue. 6,
p.
1395.
Sun, Qingfeng
and
Zhao, Rui
2019.
Bounds for GL3
L-functions in depth aspect.
Forum Mathematicum,
Vol. 31,
Issue. 2,
p.
303.
Khan, Rizwanur
Lei, Ruoyun
and
Milićević, Djordje
2019.
Effective moments of Dirichlet L-functions in
Galois orbits.
Involve, a Journal of Mathematics,
Vol. 12,
Issue. 3,
p.
475.
Vandehey, Joseph
2019.
Differencing methods for Korobov-type exponential sums.
Journal d'Analyse Mathématique,
Vol. 138,
Issue. 1,
p.
405.
Wu, Han
2019.
Burgess-like subconvexity for .
Compositio Mathematica,
Vol. 155,
Issue. 8,
p.
1457.
Banks, William D.
and
Shparlinski, Igor E.
2019.
Bounds on short character sums and L-functions with characters to a powerful modulus.
Journal d'Analyse Mathématique,
Vol. 139,
Issue. 1,
p.
239.
Pierce, Lillian B.
and
Xu, Junyan
2020.
Burgess bounds for short character sums evaluated at forms.
Algebra & Number Theory,
Vol. 14,
Issue. 7,
p.
1911.
Khan, Rizwanur
2021.
Subconvexity Bounds for TwistedL-Functions.
The Quarterly Journal of Mathematics,
Vol. 72,
Issue. 3,
p.
1133.
Wu, Jie
and
Xi, Ping
2021.
Arithmetic exponent pairs for algebraic trace functions and applications.
Algebra & Number Theory,
Vol. 15,
Issue. 9,
p.
2123.
Assing, Edgar
2021.
Adelic Voronoï summation and subconvexity for GL(2) L-functions in the depth aspect.
International Journal of Number Theory,
Vol. 17,
Issue. 07,
p.
1537.
Nunes, Ramon M
2021.
The Twelfth Moment of Dirichlet L-functions with Smooth Moduli.
International Mathematics Research Notices,
Vol. 2021,
Issue. 12,
p.
9180.
Kumar, Sumit
Mallesham, Kummari
and
Singh, Saurabh Kumar
2022.
Sub-convexity bound for $$GL(3) \times GL(2)$$ L-functions: the depth aspect.
Mathematische Zeitschrift,
Vol. 301,
Issue. 3,
p.
2229.
Banks, William
and
Shparlinski, Igor
2022.
On a conjecture of Soundararajan.
Bulletin of the London Mathematical Society,
Vol. 54,
Issue. 1,
p.
301.
Blomer, Valentin
Jana, Subhajit
and
Nelson, Paul D.
2023.
The Weyl bound for triple product L-functions.
Duke Mathematical Journal,
Vol. 172,
Issue. 6,
Ghosh, Aritra
2023.
Weyl-type bounds for twisted GL(2) short character sums.
The Ramanujan Journal,
Vol. 62,
Issue. 2,
p.
551.
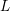 $L$-functions to prime power moduli
$L$-functions to prime power moduli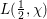 $L(\frac{1}{2},{\it\chi})$ of a Dirichlet
$L(\frac{1}{2},{\it\chi})$ of a Dirichlet 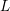 $L$-function of a character
$L$-function of a character 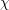 ${\it\chi}$ to a prime power modulus
${\it\chi}$ to a prime power modulus 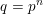 $q=p^{n}$ of the form
$q=p^{n}$ of the form 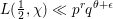 $L(\frac{1}{2},{\it\chi})\ll p^{r}q^{{\it\theta}+{\it\epsilon}}$ with a fixed
$L(\frac{1}{2},{\it\chi})\ll p^{r}q^{{\it\theta}+{\it\epsilon}}$ with a fixed  $r$ and
$r$ and 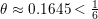 ${\it\theta}\approx 0.1645<\frac{1}{6}$, breaking the long-standing Weyl exponent barrier. In fact, we develop a general new theory of estimation of short exponential sums involving
${\it\theta}\approx 0.1645<\frac{1}{6}$, breaking the long-standing Weyl exponent barrier. In fact, we develop a general new theory of estimation of short exponential sums involving 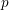 $p$-adically analytic phases, which can be naturally seen as a
$p$-adically analytic phases, which can be naturally seen as a 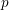 $p$-adic analogue of the method of exponent pairs. This new method is presented in a ready-to-use form and applies to a wide class of well-behaved phases including many that arise from a stationary phase analysis of hyper-Kloosterman and other complete exponential sums.
$p$-adic analogue of the method of exponent pairs. This new method is presented in a ready-to-use form and applies to a wide class of well-behaved phases including many that arise from a stationary phase analysis of hyper-Kloosterman and other complete exponential sums.

