Article contents
Classification of universal formality maps for quantizations of Lie bialgebras
Published online by Cambridge University Press: 27 November 2020
Abstract
We settle several fundamental questions about the theory of universal deformation quantization of Lie bialgebras by giving their complete classification up to homotopy equivalence. Moreover, we settle these questions in a greater generality: we give a complete classification of the associated universal formality maps. An important new technical ingredient introduced in this paper is a polydifferential endofunctor  ${\mathcal {D}}$ in the category of augmented props with the property that for any representation of a prop
${\mathcal {D}}$ in the category of augmented props with the property that for any representation of a prop 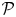 ${\mathcal {P}}$ in a vector space
${\mathcal {P}}$ in a vector space 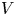 $V$ the associated prop
$V$ the associated prop 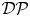 ${\mathcal {D}}{\mathcal {P}}$ admits an induced representation on the graded commutative algebra
${\mathcal {D}}{\mathcal {P}}$ admits an induced representation on the graded commutative algebra 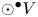 $\odot ^\bullet V$ given in terms of polydifferential operators. Applying this functor to the minimal resolution
$\odot ^\bullet V$ given in terms of polydifferential operators. Applying this functor to the minimal resolution 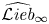 $\widehat {\mathcal {L}\textit{ieb}}_\infty$ of the genus completed prop
$\widehat {\mathcal {L}\textit{ieb}}_\infty$ of the genus completed prop 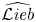 $\widehat {\mathcal {L}\textit{ieb}}$ of Lie bialgebras we show that universal formality maps for quantizations of Lie bialgebras are in one-to-one correspondence with morphisms of dg props
$\widehat {\mathcal {L}\textit{ieb}}$ of Lie bialgebras we show that universal formality maps for quantizations of Lie bialgebras are in one-to-one correspondence with morphisms of dg props
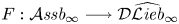 \[F: \mathcal{A}\textit{ssb}_\infty \longrightarrow {\mathcal{D}}\widehat{\mathcal{L}\textit{ieb}}_\infty \]
\[F: \mathcal{A}\textit{ssb}_\infty \longrightarrow {\mathcal{D}}\widehat{\mathcal{L}\textit{ieb}}_\infty \]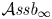 $\mathcal {A}\textit{ssb}_\infty$ is a minimal resolution of the prop of associative bialgebras. We prove that the set of such formality morphisms is non-empty. The latter result is used in turn to give a short proof of the formality theorem for universal quantizations of arbitrary Lie bialgebras which says that for any Drinfeld associator
$\mathcal {A}\textit{ssb}_\infty$ is a minimal resolution of the prop of associative bialgebras. We prove that the set of such formality morphisms is non-empty. The latter result is used in turn to give a short proof of the formality theorem for universal quantizations of arbitrary Lie bialgebras which says that for any Drinfeld associator 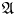 $\mathfrak{A}$ there is an associated
$\mathfrak{A}$ there is an associated  ${\mathcal {L}} ie_\infty$ quasi-isomorphism between the
${\mathcal {L}} ie_\infty$ quasi-isomorphism between the 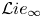 ${\mathcal {L}} ie_\infty$ algebras
${\mathcal {L}} ie_\infty$ algebras 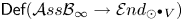 $\mathsf {Def}({\mathcal {A}} ss{\mathcal {B}}_\infty \rightarrow {\mathcal {E}} nd_{\odot ^\bullet V})$ and
$\mathsf {Def}({\mathcal {A}} ss{\mathcal {B}}_\infty \rightarrow {\mathcal {E}} nd_{\odot ^\bullet V})$ and 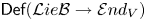 $\mathsf {Def}({\mathcal {L}} ie{\mathcal {B}}\rightarrow {\mathcal {E}} nd_V)$ controlling, respectively, deformations of the standard bialgebra structure in
$\mathsf {Def}({\mathcal {L}} ie{\mathcal {B}}\rightarrow {\mathcal {E}} nd_V)$ controlling, respectively, deformations of the standard bialgebra structure in 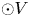 $\odot V$ and deformations of any given Lie bialgebra structure in
$\odot V$ and deformations of any given Lie bialgebra structure in 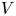 $V$. We study the deformation complex of an arbitrary universal formality morphism
$V$. We study the deformation complex of an arbitrary universal formality morphism 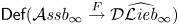 $\mathsf {Def}(\mathcal {A}\textit{ssb}_\infty \stackrel {F}{\rightarrow } {\mathcal {D}}\widehat {\mathcal {L}\textit{ieb}}_\infty )$ and prove that it is quasi-isomorphic to the full (i.e. not necessary connected) version of the graph complex introduced Maxim Kontsevich in the context of the theory of deformation quantizations of Poisson manifolds. This result gives a complete classification of the set
$\mathsf {Def}(\mathcal {A}\textit{ssb}_\infty \stackrel {F}{\rightarrow } {\mathcal {D}}\widehat {\mathcal {L}\textit{ieb}}_\infty )$ and prove that it is quasi-isomorphic to the full (i.e. not necessary connected) version of the graph complex introduced Maxim Kontsevich in the context of the theory of deformation quantizations of Poisson manifolds. This result gives a complete classification of the set 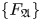 $\{F_\mathfrak{A}\}$ of gauge equivalence classes of universal Lie connected formality maps: it is a torsor over the Grothendieck–Teichmüller group
$\{F_\mathfrak{A}\}$ of gauge equivalence classes of universal Lie connected formality maps: it is a torsor over the Grothendieck–Teichmüller group 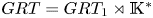 $GRT=GRT_1\rtimes {\mathbb {K}}^*$ and can hence can be identified with the set
$GRT=GRT_1\rtimes {\mathbb {K}}^*$ and can hence can be identified with the set 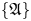 $\{\mathfrak{A}\}$ of Drinfeld associators.
$\{\mathfrak{A}\}$ of Drinfeld associators.
Keywords
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s) 2020
Footnotes
S.M. has been partially supported by the Swedish Vetenskaprådet, grant 2012-5478. T.W. has been partially supported by the Swiss National Science foundation, grant 200021_150012, and the SwissMAP NCCR funded by the Swiss National Science foundation.
References
- 6
- Cited by





