Paper
Hypergraphs Do Jump
-
- Published online by Cambridge University Press:
- 13 July 2010, pp. 161-171
-
- Article
- Export citation
Local Resilience and Hamiltonicity Maker–Breaker Games in Random Regular Graphs
-
- Published online by Cambridge University Press:
- 16 December 2010, pp. 173-211
-
- Article
- Export citation
On Barycentric Subdivision
-
- Published online by Cambridge University Press:
- 24 November 2010, pp. 213-237
-
- Article
- Export citation
Pegging Graphs Yields a Small Diameter
-
- Published online by Cambridge University Press:
- 24 August 2010, pp. 239-248
-
- Article
- Export citation
A Lower Bound for the Size of a Minkowski Sum of Dilates
-
- Published online by Cambridge University Press:
- 06 December 2010, pp. 249-256
-
- Article
- Export citation
The Dual BKR Inequality and Rudich's Conjecture
-
- Published online by Cambridge University Press:
- 02 December 2010, pp. 257-266
-
- Article
- Export citation
Graphs, Links, and Duality on Surfaces
-
- Published online by Cambridge University Press:
- 29 September 2010, pp. 267-287
-
- Article
- Export citation
Period Lengths for Iterated Functions
-
- Published online by Cambridge University Press:
- 16 September 2010, pp. 289-298
-
- Article
- Export citation
New Graph Polynomials from the Bethe Approximation of the Ising Partition Function
-
- Published online by Cambridge University Press:
- 30 June 2010, pp. 299-320
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
CPC volume 20 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 28 January 2011, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
CPC volume 20 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 28 January 2011, pp. b1-b2
-
- Article
-
- You have access
- Export citation




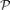
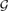
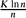 then, with high probability, the local resilience of
then, with high probability, the local resilience of 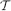
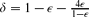 . (A key part of the proof is a correlation-like inequality on events in a finite product probability space that is in some sense dual to Reimer's inequality [11], a.k.a. the BKR inequality [5], or the van den Berg–Kesten conjecture [3].)
. (A key part of the proof is a correlation-like inequality on events in a finite product probability space that is in some sense dual to Reimer's inequality [11], a.k.a. the BKR inequality [5], or the van den Berg–Kesten conjecture [3].)